Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Содержание
- 1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- 2. Лекция 3.1Дифференцируемость функции в точке. Связь дифференцируемости
- 3. ОПРЕДЕЛЕНИЕ. Функция f(x), определенная в U(x0), называется
- 4. Определение производной функции в точке. ОПРЕДЕЛЕНИЕ. Пусть
- 5. ТЕОРЕМА. Для того чтобы функция f(x) была
- 6. Достаточность. Пусть f(x) имеет производную в точке
- 7. ЗАМЕЧАНИЕ. Приращение Δх часто обозначают символом dх
- 8. ТЕОРЕМА. Если функция f(x) дифференцируема в точке
- 9. ЗАМЕЧАНИЕ. Непрерывность функции в точке не является
- 10. Пример 2.11- 1- 10xy→ 0 при
- 11. Геометрический смысл производной и дифференциала. Пусть функция f(x)
- 12. Если функция дифференцируема в точке х0, то
- 13. Из уравнения касательной, в частности, получим у
- 14. Физические приложения производной и дифференциала.Если S(t) –
- 15. Правила дифференцирования.Дифференцирование суммы, произведения и частного ТЕОРЕМА . Если
- 16. Пусть у = f⋅g. ТогдаПусть у = f / g. Тогда
- 17. Дифференцирование обратной функцииТЕОРЕМА Если функция у = f(x)
- 18. Заметим, что Δу ≠ 0, если Δх
- 19. Дифференцирование сложной функции ТЕОРЕМА Пусть функция у = f(x)
- 20. Здесь Δх→ 0 при Δt→0 в силу
- 21. СПАСИБО ЗА ВНИМАНИЕ!
- 22. ЗАМЕЧАНИЕ 2. Δy = f(xo + Δx)
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Лекция 3.1
Дифференцируемость функции в точке.
Связь дифференцируемости и непрерывности.
Геометрический
и физический смысл производной и дифференциала.
Слайд 3 ОПРЕДЕЛЕНИЕ.
Функция f(x), определенная в U(x0), называется дифференцируемой в точке
х0, если ее приращение при переходе из точки хо в
точку х = х0+Δх можно представить в видеΔy = f(x0 + Δx) – f(x0) = А(x0)Δx + о(Δx) при Δх→0,
где А(x0) – не зависит от Δx .
Главная линейная относительно Δx часть приращения функции А(x0)Δx – называется дифференциалом функции в точке х0 при приращении Δx и обозначается df(х0; Δx) или df(х0) или df или dу.
Таким образом
Δy = f(x0 + Δx) – f(x0) = df(х0; Δx) + о(Δx) при Δх→0.
Дифференцируемость функции в точке. Дифференциал.
Слайд 4Определение производной функции в точке.
ОПРЕДЕЛЕНИЕ.
Пусть функция f(x) определена
в U(x0) и х – произвольная точка этой окрестности. Если
существует предел отношенияпри х → х 0, то этот предел называется производной функции f(x) в точке х0 и обозначается f '(x0), то есть
Пусть Δx = x – x0 – приращение аргумента при переходе из точки х0 в точку х, а Δy = f(x0+Δx) – f(x0) – соответствующее приращение функции.
Тогда
предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Слайд 5 ТЕОРЕМА.
Для того чтобы функция f(x) была дифференцируема в точке
x0, необходимо и достаточно, чтобы она имела производную в этой
точке.При этом дифференциал и производная связаны равенством:
df(х0; Δx) = f '(x0) Δх.
Доказательство.
Необходимость.
Пусть f(x) дифференцируема в точке xo, то есть
Δy = f(x0 + Δx) – f(x0) = А(x0)Δx + о(Δx) при Δх → 0,
откуда
Δy /Δx = А(x0) + о(1) при Δх→0,
следовательно существует
то есть функция имеет в точке x0 производную f '(x0) = А(x0).
Связь между дифференцируемостью функции в точке и существованием производной в этой точке.
Слайд 6Достаточность.
Пусть f(x) имеет производную в точке xo, то есть
существует
Следовательно
Δy /Δx = f '(x0) + о(1) при Δх
→ 0,откуда
Δy = f '(x0) Δх + о(Δх) при Δх → 0,
то есть функция дифференцируема в точке x0 и
df(х0; Δx) = f '(x0) Δх.
ЗАМЕЧАНИЕ.
Операция вычисления производной называется дифференцированием.
Слайд 7ЗАМЕЧАНИЕ.
Приращение Δх часто обозначают символом dх и называют дифференциалом
независимой переменной. Таким образом, дифференциал функции в точке x0 можно
записать в видеdf(х0) = f '(x0) dх.
Если функция дифференцируема в каждой точке некоторого интервала, то ее дифференциал dy – функция от х и dx:
dy = f '(x) dx.
Отсюда, в частности, получается выражение для производной
То есть производную можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
Слайд 8 ТЕОРЕМА.
Если функция f(x) дифференцируема в точке x0, то она
непрерывна в этой точке.
Доказательство.
Пусть существует
Тогда
Отсюда получим, что
f (x)
– f (x0) = (f '(x0) + о(1)) (х – х0) → 0 при х → х0 . то есть f(x) непрерывна в точке x0.
Непрерывность дифференцируемой функции.
Слайд 9 ЗАМЕЧАНИЕ.
Непрерывность функции в точке не является достаточным условием существования
в этой точке производной.
Пример 1. f (x) = ⎜х
⎜. Функция непрерывна в точке х = 0.
Рассмотрим
x
y
0
Предел не существует, так как
Итак, функция f (x) = ⎜х ⎜не имеет производной в точке
х = 0, хотя непрерывна в этой точке.
Слайд 10Пример 2.
1
1
- 1
- 1
0
x
y
→ 0 при х → 0.
→ ∞ при х → 0.
Т.е. f(x) непрерывна
в точке х = 0. Т.е. f(x) не имеет производной в точке х = 0 и, следовательно,
не дифференцируема в этой точке.
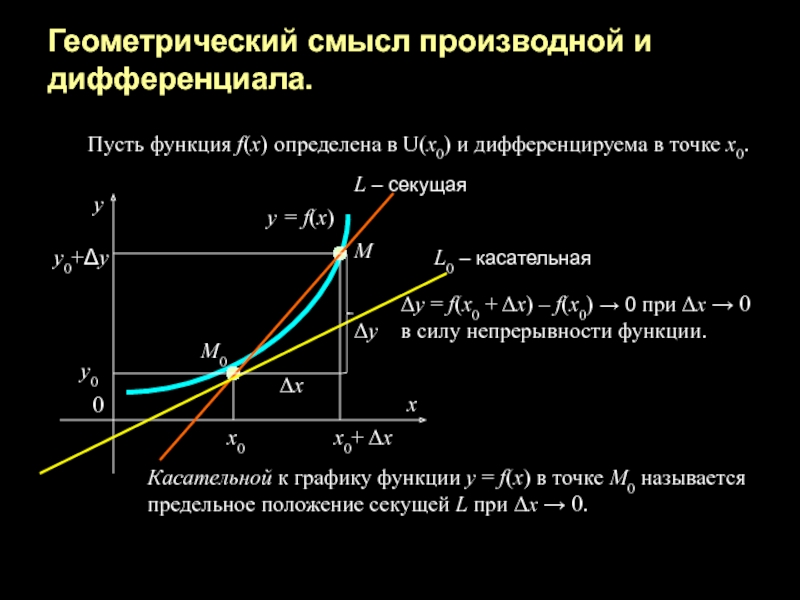
Слайд 11Геометрический смысл производной и дифференциала.
Пусть функция f(x) определена в U(x0)
и дифференцируема в точке х0.
М0
М
x0
x0+ Δx
Δy
Δx
y = f(x)
y0
y0+Δу
0
L
– секущая L0 – касательная
x
Δy = f(x0 + Δx) – f(x0) → 0 при Δх → 0
в силу непрерывности функции.
Касательной к графику функции у = f(x) в точке М0 называется
предельное положение секущей L при Δх → 0.
y
Слайд 12 Если функция дифференцируема в точке х0, то в уравнении секущей
Δу/Δх → f ′(x0) при Δх → 0
и уравнение
касательной имеет вид у = у0 + f ′(x0) (х – х0).
Если же
Δу/Δх → ∞ при Δх → 0,
то прямая
х = х0 ,
получающаяся из уравнения секущей, называется вертикальной
касательной к графику функции в точке М0.
Нормалью к графику функции в точке М0 называется прямая,
перпендикулярная касательной, проходящая через точку М0.
Ее уравнение имеет вид
у = у0 – 1/f ′(x0) (х – х0).
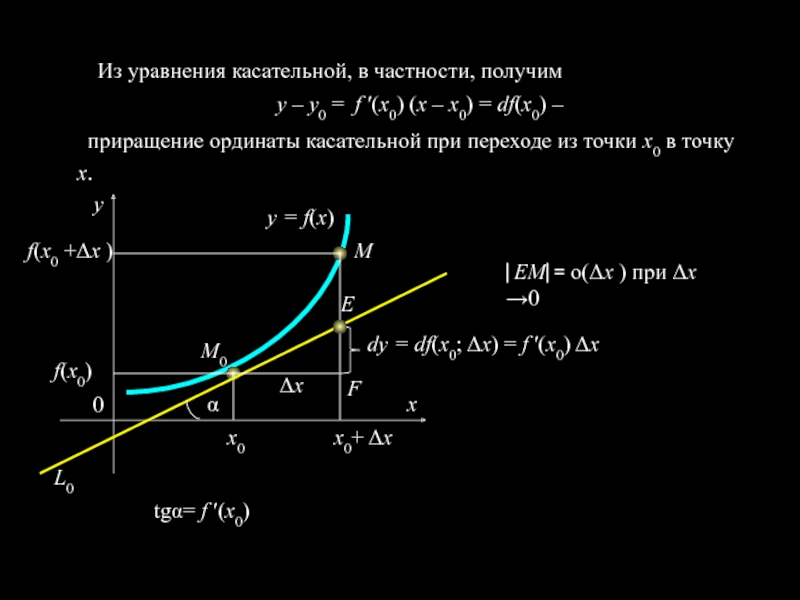
Слайд 13 Из уравнения касательной, в частности, получим
у – у0 =
f ′(x0) (х – х0) = df(х0) –
приращение ординаты касательной
при переходе из точки х0 в точку х.М0
М
x0
x0+ Δx
dy = df(х0; Δx) = f ′(x0) Δx
Δx
y = f(x)
f(x0)
f(x0 +Δx )
0
x
y
F
E
⎜EM⎜= o(Δx ) при Δx →0
α
L0
tgα= f ′(x0)
Слайд 14Физические приложения производной и дифференциала.
Если S(t) – путь, пройденный материальной
точкой за время t, то S '(t) – мгновенная скорость
материальной точки, а dS = S '(t)dt – расстояние, которое прошла бы материальная точка за промежуток времени от t до t + dt, если бы она двигалась со скоростью, равной мгновенной скорости в момент t.Если Q(t) – количество электричества, протекающего через поперечное сечение проводника в момент времени t, то Q '(t) = I – сила тока.
Если N(t) – количество вещества, образующегося в момент t в ходе химической реакции, то N '(t) – скорость химической реакции.
Слайд 15Правила дифференцирования.
Дифференцирование суммы, произведения и частного
ТЕОРЕМА .
Если функции f и
g дифференцируемы в точке х, то в этой точке дифференцируемы
f + g, f⋅g, f /g (если g(x) ≠ 0) и при этом(f(х) + g(х))' = f '(х) + g '(х)
(f(х)⋅g(х))' = f '(х)⋅g(х) + f (х)⋅g '(х)
(f (х) /g(х))' = (f '(х)⋅g(х) – f (х)⋅g'(х))/g2(х)
Следствие.
Доказательство теоремы.
1. Пусть у = f + g. Тогда
Если f (х) дифференцируема в точке х и С = const, то
(С⋅f(x))' = С⋅f '(x);
(f(x)/С)' = f '(x)/С.
Слайд 17Дифференцирование обратной функции
ТЕОРЕМА
Если функция у = f(x) непрерывна и строго
монотонна на отрезке [x0- δ, x0 + δ] и имеет
производную f '(x0) ≠ 0, тогда обратная к ней функция x = g(y) дифференцируема в точке у0 = f(x0), причемg '(y0) = 1/ f '(x0).
Доказательство.
Пусть f(x) строго возрастает на отрезке [x0- δ, x0+ δ].
Пусть α = f(x0- δ), β = f(x0+ δ).
Тогда на отрезке [α, β] определена обратная функция x = g(y),
непрерывная и строго возрастающая, причем f(x0)∈ (α, β).
x0
x0 - δ
x0 + δ
α
β
у0=f(x0)
x
y
Δx
Δу
у = f(x)
x = g(y)
Пусть Δу таково, что у0+Δу ∈ (α, β).
Обозначим Δх = g(y0+Δу) - g(y0).
Нужно доказать, что существует
0
Слайд 18 Заметим, что Δу ≠ 0, если Δх ≠ 0, в
силу строгой монотонности функции. Поэтому при Δу ≠ 0 имеем:
Пусть
Δу → 0, тогда и Δх → 0 , так как функция x = g(y) непрерывна в точке у0. Но если Δх → 0, то существует Итак, правая часть тождества имеет предел, равный 1/f ' (x0).
Следовательно, существует и
Слайд 19Дифференцирование сложной функции
ТЕОРЕМА
Пусть функция у = f(x) дифференцируема в точке
x0, у0 = f(x0),
а функция x = ϕ (t)
дифференцируема в точке t0 , x0 = ϕ ( to). Тогда сложная функция у = f (ϕ (t)) дифференцируема в точке t0 и
f 't (ϕ ( t0)) = f 'x (x0)·ϕ 't ( t0)
или
Доказательство.
Δy = f(x) – f(x0) = f '(x0)Δx + о(Δx) при Δх → 0,
Δx = ϕ (t) – ϕ (t0) = ϕ '(t0)Δt + о(Δt) при Δt → 0,
Δy = f (ϕ (t)) – f (ϕ (t0)) = f '(x0)( ϕ '(t0 )Δt + о(Δt)) + о(Δx) =
= f '(x0)ϕ '( t0 )Δt + f '(x0)о(Δt)+ о(Δx)
Слайд 20
Здесь Δх→ 0 при Δt→0 в силу непрерывности функции ϕ
(t) в точке t0.
при Δt→0.
Следовательно
ЗАМЕЧАНИЕ.
Правило вычисления производной сложной функции распространяется
на композицию любого конечного числа функций. Например:
(f (ϕ (g(x))))' = f '(ϕ (g(x)))⋅ϕ'(g(x))⋅g'(x).
Слайд 22ЗАМЕЧАНИЕ 2.
Δy = f(xo + Δx) – f(xo) =
f '(xo) Δx + о(Δx) ≈ f '(xo) Δx
⇒f(xo + Δx) ≈ f(xo) + f '(xo) Δx.
Последнюю формулу можно использовать для вычисления приближенного значения f(xo + Δx) при малых Δx, если известны значения f(xo) и f '(xo).
Пример.