Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамическое программирование Оптимальные деревья поиска
Содержание
- 1. Динамическое программирование Оптимальные деревья поиска
- 2. 03.03.2014Динамическое программированиеПример 3. Оптимальные деревья поискаСм. начало
- 3. Оптимальные деревья поискаРанее при рассмотрении БДП, как
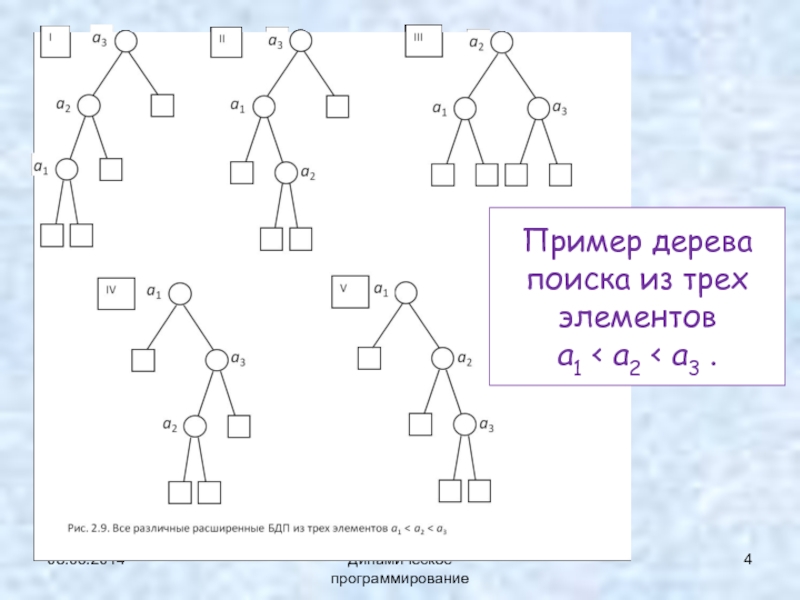
- 4. 03.03.2014Динамическое программированиеПример дерева поиска из трех элементов a1
- 5. Заданы вероятности предъявления элемента x для поиска:
- 6. Постановка задачиПоиск будет осуществляться среди набора данных a1, a2, …, an–1, an. Пусть последовательность упорядочена: a1
- 7. Все эти 2n + 1 событий (исходов поиска) могут быть упорядочены: B0
- 8. Тогда среднее число (математическое ожидание) сравнений при
- 9. Такое дерево называют оптимальным БДП. Есть ли
- 10. Очевидное решение поставленной задачи состоит в переборе
- 11. Конец повторения прошлой лекцииРешение поставленной задачи на следующей лекции.03.03.2014Динамическое программирование
- 12. Построение оптимальных деревьев поискаДано: набор элементов a1
- 13. Пусть имеется оптимальное дерево. Согласно принципу оптимальности,
- 14. ИдеяTij -поддерево БДП из элементов(при 0 ≤ i ≤ j
- 15. ОбозначенияПусть l = l(rij)- уровень корня rij поддерева
- 16. Вклад поддерева Tij в стоимость C0,nгдеCij - стоимость поддерева Tij. wij - вес поддерева Tij.03.03.2014Динамическое программирование
- 17. Идея: структура дерева + принцип оптимальности03.03.2014Динамическое программирование
- 18. Преобразование+wij не зависит от структуры поддерева Tij 03.03.2014Динамическое программирование
- 19. Cii = 0разности индексов k – 1 − i и j – k в слагаемых
- 20. Таблица (аналогия с задачей о перемножении цепочки матриц)03.03.2014Динамическое программирование
- 21. for (i =0; i
- 22. См. пример в файле «2_08_ОДП.doc»С.67,68-…03.03.2014Динамическое программирование
- 23. Построение БДПBinT MakeOptBST (int i, j ){ int k; ElemBinT
- 24. Модификация Д.Кнута ri,j −1 ≤ rij ≤ ri +1,j 03.03.2014Динамическое программированиеВместо k = (i +1)
- 25. См. с.7203.03.2014Динамическое программирование
- 26. 03.03.2014Динамическое программированиеКОНЕЦ ЛЕКЦИИКОНЕЦ ЛЕКЦИИКОНЕЦ
- 27. Скачать презентанцию
03.03.2014Динамическое программированиеПример 3. Оптимальные деревья поискаСм. начало в Лекции 3.См. также раздел 2.8 пособия «Деревья кодирования и поиска»
Слайды и текст этой презентации
Слайд 103.03.2014
Динамическое программирование
Построение и анализ алгоритмов
Лекция 4
Динамическое программирование
Оптимальные деревья поиска
Слайд 203.03.2014
Динамическое программирование
Пример 3. Оптимальные деревья поиска
См. начало в Лекции 3.
См.
также раздел 2.8
Слайд 3Оптимальные деревья поиска
Ранее при рассмотрении БДП, как правило, предполагалось, что
для поиска различные ключи предъявляются с равной вероятностью.
Пусть теперь заранее
известно, что некоторые ключи предъявляются чаще других. Тогда расположение «частых» ключей ближе к корню дерева сократит время их поиска и, возможно, среднее время поиска (по разным предъявлениям ключей).
03.03.2014
Динамическое программирование
Слайд 5Заданы вероятности предъявления элемента x для поиска: P (x = a1) = α; P
(x = a2) = β; P (x = a3) = γ.
03.03.2014
Динамическое программирование
Среднее (по всем предъявлениям x) число
сравнений (стоимость) в случаях успешного поиска как функция переменных α, β и γ, 
Слайд 6Постановка задачи
Поиск будет осуществляться среди набора данных a1, a2, …, an–1, an.
Пусть последовательность
упорядочена:
a1
Ai : (x = ai) для i ∈ 1..n, B0, …, Bn - события, соответствующие вариантам неудачных исходов поиска,
т. е. Bi : (ai < x < ai+1) для i ∈ 0..n.
Здесь для упрощения записи событий B0 и Bn добавлены фиктивные элементы a0 = −∞ и an+1 = +∞, которые не должны использоваться в алгоритме.
03.03.2014
Динамическое программирование
Слайд 7Все эти 2n + 1 событий (исходов поиска)
могут быть
упорядочены:
B0
i ∈ 1..n, и qi = P (Bi) для i ∈ 0..n. При этом Σi∈1..n pi + Σi∈0..n qi = 1.
События Ai соответствуют внутренним узлам расширенного дерева поиска, а события Bi – внешним узлам (листьям) расширенного дерева поиска.
03.03.2014
Динамическое программирование
Постановка задачи (продолжение)
Слайд 8Тогда среднее число (математическое ожидание) сравнений при поиске можно записать
в виде
где l (x) – уровень узла x (или длина
пути от корня до узла x) в БДП. Здесь уровень узла определен так, что l (корень) = 0.
03.03.2014
Динамическое программирование
Постановка задачи (продолжение)
Итак, задача состоит в том, чтобы по заданным весам
построить БДП, минимизирующее значение C0,n .
Слайд 9Такое дерево называют оптимальным БДП.
Есть ли сходство этой задачи
с задачей построения оптимального префиксного кода ?
В чём сходство, в
чём различие?Ответ.
03.03.2014
Динамическое программирование
Постановка задачи (продолжение)
Слайд 10Очевидное решение поставленной задачи состоит в переборе всех структурно различных
бинарных деревьев с n узлами и выборе дерева с наименьшей
стоимостью C0,n .Однако поскольку (см. лекции про БДП) число bn структурно различных бинарных деревьев с n узлами есть
, то этот способ вряд ли будет иметь практическую ценность.
Оказывается, приемлемое по количеству вычислений решение данной задачи может быть получено методом динамического программирования.
03.03.2014
Динамическое программирование
Слайд 11Конец повторения прошлой лекции
Решение поставленной задачи
на следующей лекции.
03.03.2014
Динамическое программирование
Слайд 12Построение оптимальных деревьев поиска
Дано:
набор элементов a1
по заданным весам построить БДП, минимизирующее значение C0,n.
03.03.2014
Динамическое программирование
Слайд 13Пусть имеется оптимальное дерево.
Согласно принципу оптимальности, лежащему в основе
метода динамического программирования, левое и правое поддеревья этого дерева в
свою очередь также должны быть оптимальны.03.03.2014
Динамическое программирование
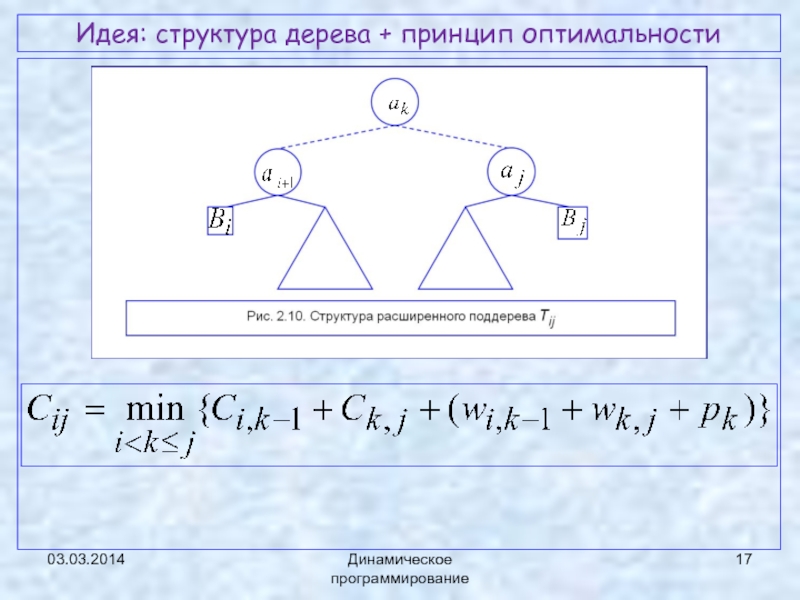
Идея
Слайд 14Идея
Tij -поддерево БДП из элементов
(при 0 ≤ i ≤ j ≤ n).
корнем поддерева
может быть любой из элементов , т. е. k ∈ i +1..j.
03.03.2014
Динамическое программирование
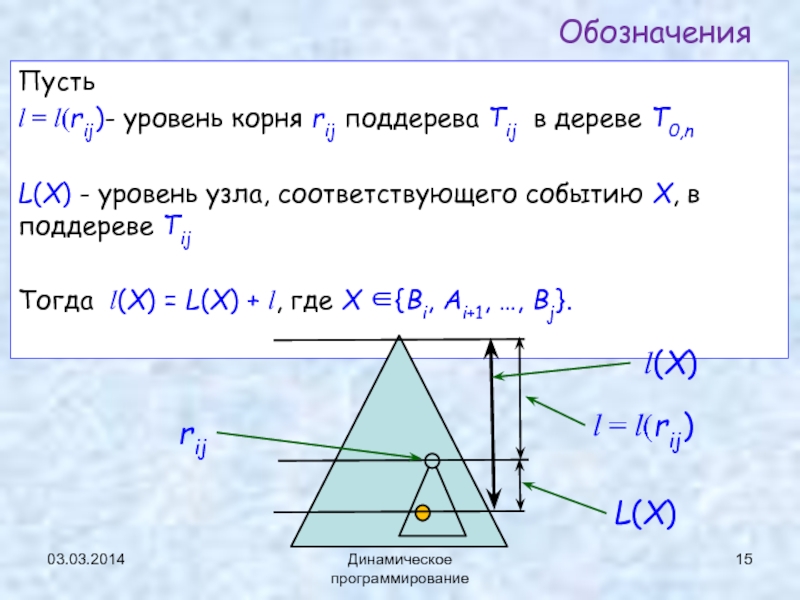
Слайд 15Обозначения
Пусть
l = l(rij)- уровень корня rij поддерева Tij в дереве
T0,n
L(X) - уровень узла, соответствующего событию X, в поддереве Tij
Тогда l(X) = L(X) + l, где X ∈{Bi, Ai+1, …, Bj}.
03.03.2014
Динамическое программирование
l = l(rij)
rij
L(X)
l(X)
Слайд 16Вклад поддерева Tij в стоимость C0,n
где
Cij - стоимость поддерева Tij.
wij - вес поддерева Tij.
03.03.2014
Динамическое программирование
Слайд 18Преобразование
+
wij не зависит от структуры поддерева Tij
03.03.2014
Динамическое программирование
Слайд 19
Cii = 0
разности индексов k – 1 − i и j – k в слагаемых Ci,k−1 и Ck,j
меньше, чем разность индексов j – i в Cij.
L = j – i ,
L=0..n03.03.2014
Динамическое программирование
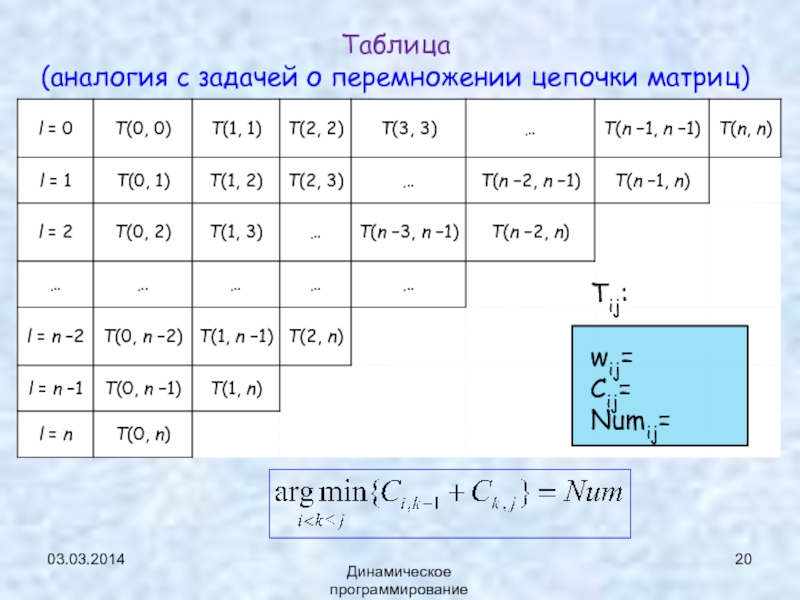
Слайд 20Таблица
(аналогия с задачей о перемножении цепочки матриц)
03.03.2014
Динамическое программирование
Слайд 21for (i =0; i
for (L=1; L
// заполнение T(i, j):w[i][ j] = w[i][j −1] + (p[j]+q[j]);
c[i][j] = +∞;
for (k =i +1 ; k< j-1; k++) { s = c[i][k −1] + c [k][j];
if (s < c[i][j] ){
c[i][j] = s;
num[i][j] = k
};
}
c[i][j] = c[i][j] + w[i][j];
}
}
03.03.2014
Динамическое программирование
n 2/2 элементов памяти и n 3/3 выполнений тела внутреннего цикла
Вычисление таблицы
Слайд 23Построение БДП
BinT MakeOptBST (int i, j )
{ int k; ElemBinT root;
BinT
L, R;
k = num[i ][j ]; root = a[k];
if (i
R = MakeOptBST (k, j);else R = NULL;
return ConsBT (root, L, R);
} //MakeOptBST
со стартовым вызовом T = MakeOptBST (0, n).
03.03.2014
Динамическое программирование
![Построение БДПBinT MakeOptBST (int i, j ){ int k; ElemBinT root; BinT L, R; k = num[i ][j ]; root = a[k]; if (i](/img/thumbs/ee347dbaaaba5cac13f1d97bb35a2b59-800x.jpg "Динамическое программирование Оптимальные деревья поиска Построение БДПBinT MakeOptBST (int i, j ){ int k; ElemBinT root; BinT L, R; k = num[i ][j ]; root = a[k]; if (i")
Слайд 24Модификация Д.Кнута
ri,j −1 ≤ rij ≤ ri +1,j
03.03.2014
Динамическое программирование
Вместо k = (i +1) .. j ⇒
k = num[i ][j −1] .. num[i +1][j ]
![Модификация Д.Кнута ri,j −1 ≤ rij ≤ ri +1,j 03.03.2014Динамическое программированиеВместо k = (i +1) .. j ⇒ k = num[i ][j −1] .. num[i +1][j](/img/thumbs/a01f28323fd7260b7fb59567c8f26d50-800x.jpg "Динамическое программирование Оптимальные деревья поиска Модификация Д.Кнута ri,j −1 ≤ rij ≤ ri +1,j 03.03.2014Динамическое программированиеВместо k = (i +1) .. j ⇒ k =")
Слайд 2603.03.2014
Динамическое программирование
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ
ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
