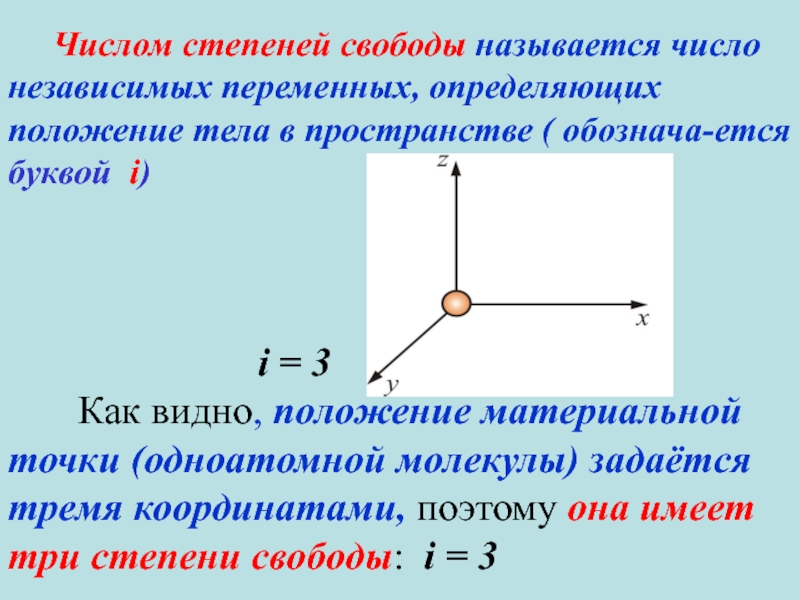
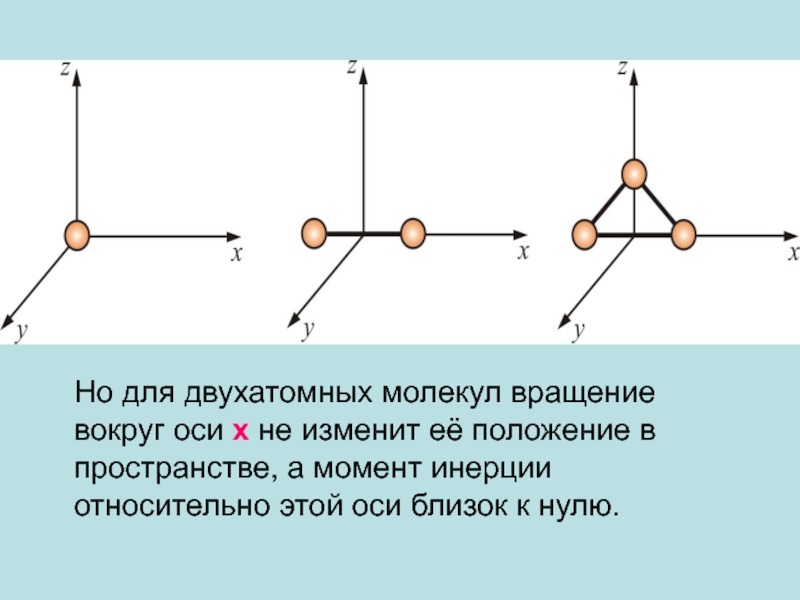
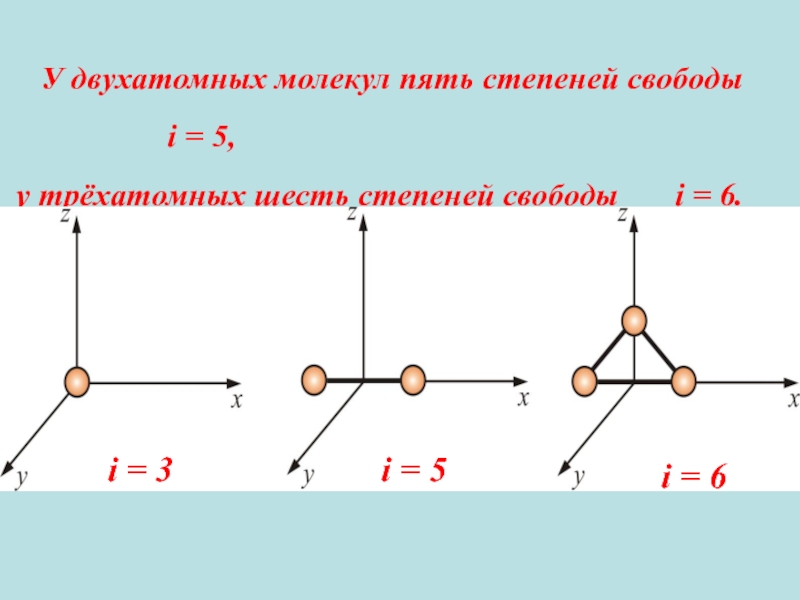
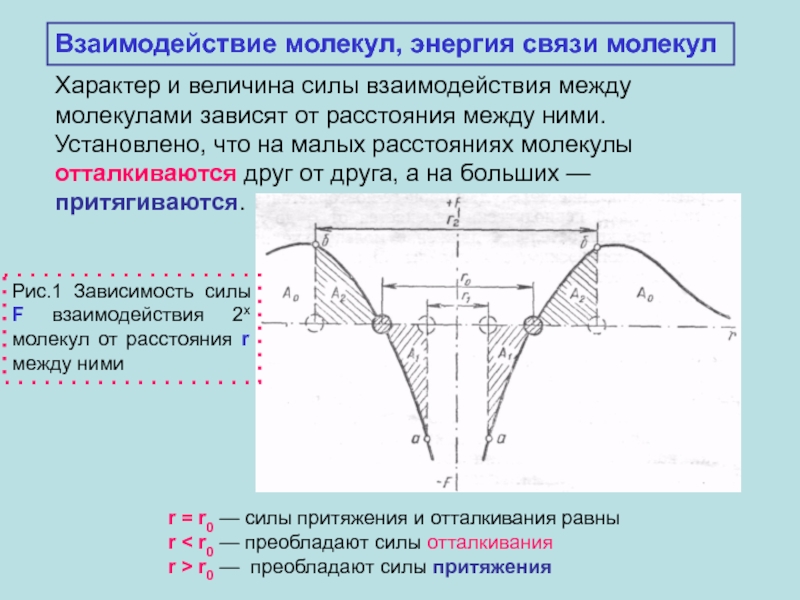
появлением нормальной составляющей скорости частиц жидкости.
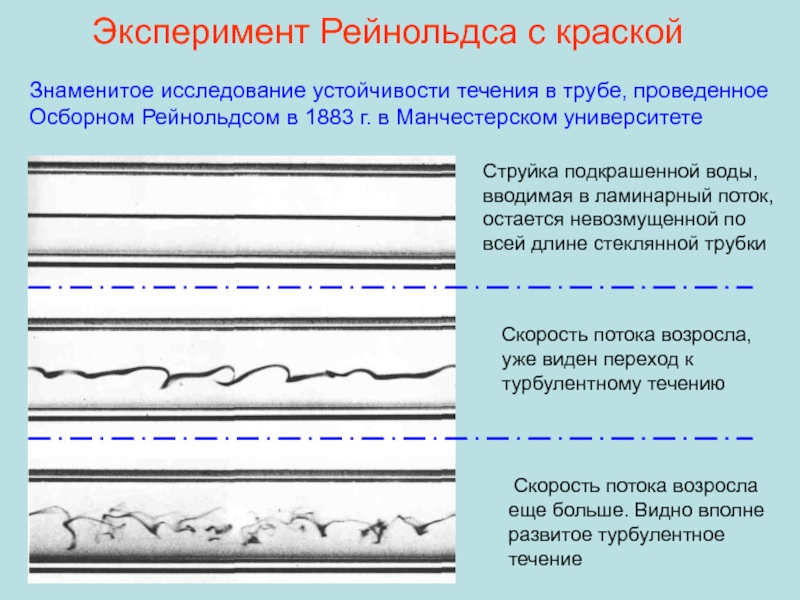
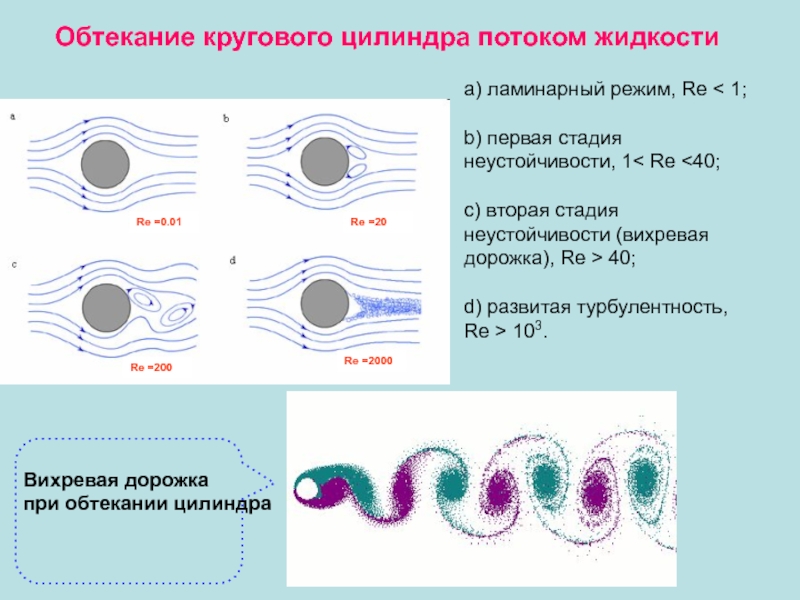
Ламинарное и турбулентное течение
1.
Ламинарное (слоистое) течение – когда слои жидкости перемещаются не смешиваясь. Оно характерно для малых скоростей и небольшой вязкости η.число Рейнольдса
ρ –плотность жидкости, υ – средняя (по сечению трубы) скорость потока, η – коэффициент вязкости жидкости, r– радиус трубы
η/ρ -кинематическая вязкость
Re < 1000
Re > 1000



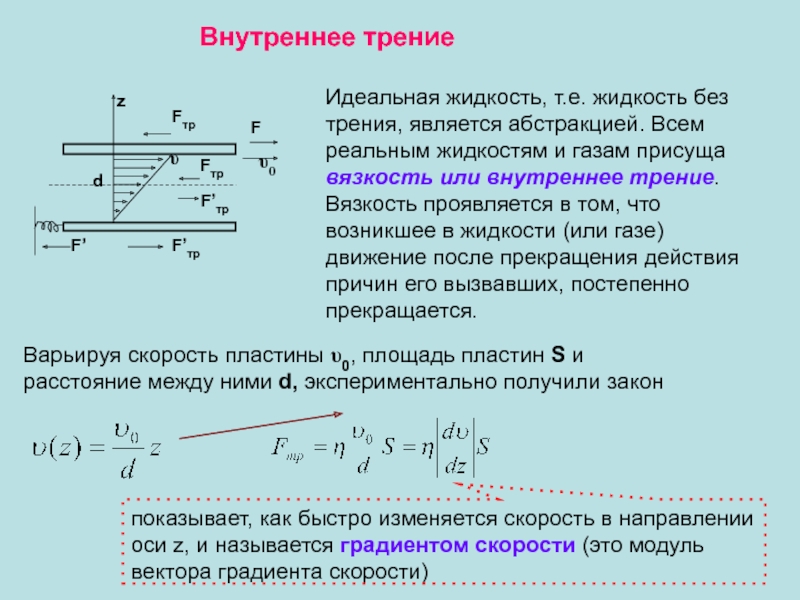
![Динамика жидкости Единица вязкости [η]= [Па·с] это вязкость, при которой градиент скорости с Единица вязкости [η]= [Па·с] это вязкость, при которой градиент скорости с модулем равным 1м/с на 1м приводит](/img/thumbs/229de796532f31fa5cfbc0a7ded61535-800x.jpg)