Дискретная случайная величина

каждом испытании не зависит от исходов других испытаний , то

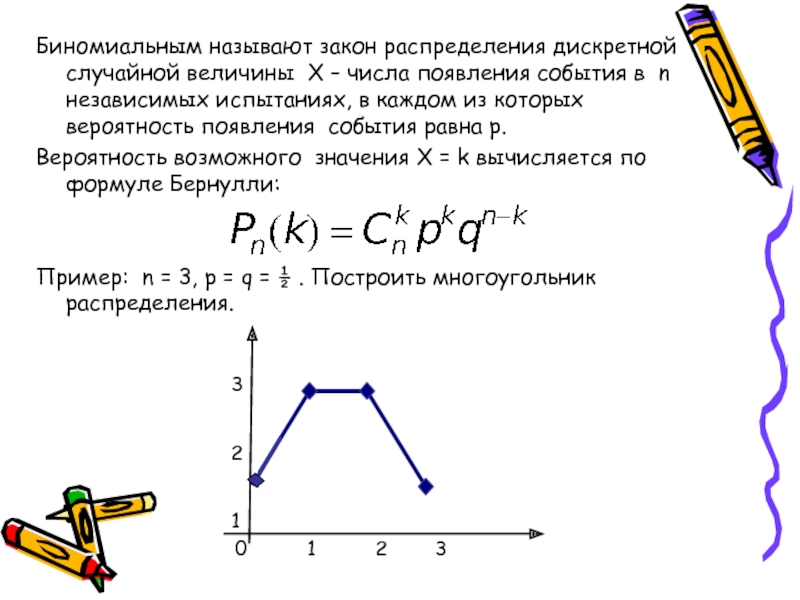
такие испытания называют независимыми относительно события А.
Будем предполагать далее, что Р(А) = р, т.е. вероятность р всегда одинакова (0 < р < 1), и поставим задачу вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз. Ответ на этот вопрос дает формула Бернулли.

из которых вероятность Р(А) = р одинакова ) событие А

наступит ровно k раз ( в любой последовательности), равна


, где



В частности,

партии из 6 или 4 партии из 8 ? (ничьи

во внимание не принимаются).
Играют два равносильных шахматиста, поэтому вероятность выигрыша в одной партии равна ½. Следовательно , вероятность проигрыша q = ½ .
Вероятность р одинакова. Последовательность выигрыша не играет роли. Значит, применим формулу Бернулли.
Вероятность того, что будут выиграны 3 партии из 6 :


Вероятность того, что будут выиграны 4 партии из 8:

Нетрудно видеть, что

k раз

II) Событие А наступит не более k раз

III) Событие

А наступит более k раз

IV) Событие А наступит не менее k раз

Нетрудно видеть, что

V) Событие А наступит не менее и не более раз

:
а) менее 2-х раз
б) не менее 2-х раз
Вероятность того, что

в каждом испытании выпадет «герб» р = ½ , q = 1-p = ½ , n=5
a)








б)

значения.
Дискретные случайные величины
Определение: Дискретной называют случайную величину , возможные значения

которой есть отдельные изолированные числа, причем величина принимает эти значения с определенными вероятностями.
Возможные значения дискретной случайной величины можно пронумеровать.
Определение: Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.

распределения.

Графический
В прямоугольной системе координат строят точки

и соединяют их отрезками прямых. Полученную ломаную называют многоугольником распределения

Способы задания закона распределения случайной величины

появления события в n независимых испытаниях, в каждом из которых

вероятность появления события равна р.
Вероятность возможного значения X = k вычисляется по формуле Бернулли:


Пример: n = 3, p = q = ½ . Построить многоугольник распределения.

0 1 2 3

3

2

1

события в каждом испытании очень мала ( р ≤ 0,1)

, то используют приближенную формулу:



где k – число появлений события в n независимых испытаниях,
- (среднее число появлений события в испытаниях).
Говорят тогда, что случайная величина распределена по закону Пуассона

,

появлений «герба» при 2-х бросаниях монеты
n=2, p = ½ ;

q = ½ ; X = 0 ; 1 ; 2.





Итак,
Проверка условия

однако часто не известен.
Но для решения многих задач достаточно знать

числовые характеристики случайной величины.
Важнейшая из них – математическое ожидание.
Оно приближенно равно среднему значению случайной величины. Если математическое ожидание числа выбиваемых очков I-го стрелка больше, чем у II-го, то I-ый лучше стреляет, чем II-ой.

M(C) = C, C=const
2. M(CX) = CM(X)
3. M(XY) =

M(X)M(Y)
4. M(X+Y) = M(X) + M(Y)

распределения:




М(Х) = 3∙0,1 + 5∙0.6 + 2∙0,3 = 3,9
2.



М(Х) =

-4∙0,2 + 0,3∙.6 + 0,5∙10 = 6
3. Z = X + 2Y, M(X) = 5, M(Y) = 3 | M(Z) = ?

M(Z) = M(X + 2Y) = M(X) + M(2Y) = M(X) + 2M(Y) = 5+6 = 11

Примеры

= 0; М(У) = -100∙0,5 + 100∙0,5 = 0
т. е.

математические ожидания равны, но возможные значения сильно различаются. Математическое ожидание полностью случайную величину не характеризует.
Для того, чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, используют числовую характеристику, которую называют дисперсией.
Если Х-М(Х) – есть отклонение случайной величины от ее математического ожидания, то дисперсией случайной величины Х называют математическое ожидание квадрата отклонения.

,

распределения:

, D(X) = ?







D(X) = 13,3 – 12,25 = 1,05

случайной величины, вычисляют не дисперсию, а среднее квадратическое отклонение


ПРИМЕРЫ:
1.