Турбулентность

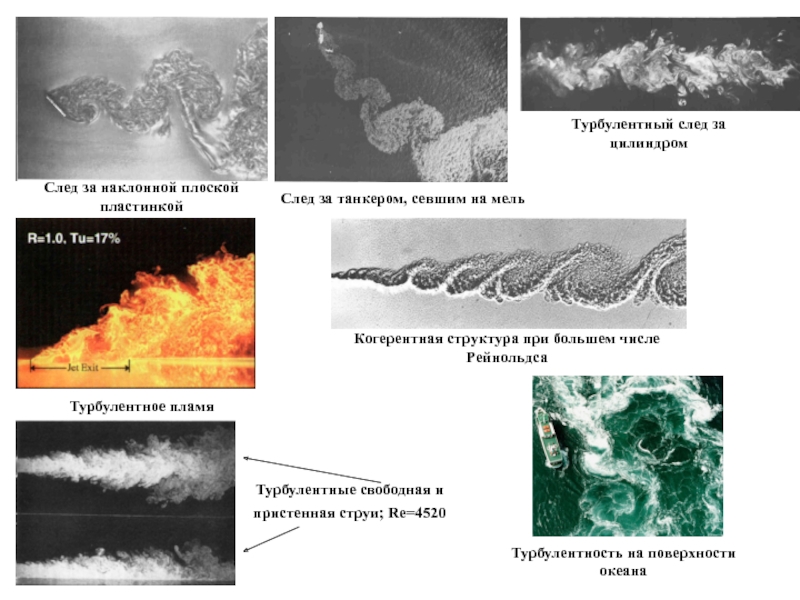
мель
Турбулентный след за цилиндром
Когерентная структура при большем числе

Рейнольдса

Турбулентное пламя

Турбулентные свободная и пристенная струи; Re=4520

Турбулентность на поверхности океана

при Re>Reкр;
турбулентность развивается в пространстве и во времени;
турбулентность

характеризуется хаотическим изменением гидродинамических величин, поэтому может быть описана случайными функциями координат и времени;
турбулентность характеризуется иногда перемежаемостью – установлением в некоторых точках пространства или в некоторые промежутки времени квазиламинарного режима;
турбулентность при больших числах Рейнольдса иногда проявляет эффекты когерентности – установление в течениях регулярных пространственно-временных структур.

потоке есть:
где - постоянная Кармана. Получим связь этой средней

скорости с перепадом давления. Средняя сила трения на стенки есть . Суммарная сила трения на стенки трубы длиной L есть . Откуда баланс трения и работы сил давления получается в форме:

Откуда, сравнивая уравнения (*) (**), получаем:

(*)

(**)

Соотношение (***) носит название закона сопротивления трубы

(***)

последнего коэффициента определяется по формуле:
Можно сравнить коэффициенты сопротивления в трубе

для ламинарного и турбулентного течений.

Нетрудно видеть, что сопротивление в ламинарном потоке сильнее падает с ростом числа Рейнольдса, чем в турбулентном! При этом при критическом числе Re* наблюдается скачок сопротивления!

Кармана-Прандтля (1930-1932гг.), можно записать для скорости в турбулентном погранслое:
ламинарный
переходный
турбулентный


Ламинарный
подслой
-

скорость пульсационного движения

Коэффициент сопротивления пластины:

Исключая скорость , получим выражение для вычисления коэффициента сопротивления пластины:

которое описывается как турбулентные пульсации различных масштабов (т.е. движений с

заметным изменением скорости на таких масштабах). С увеличением числа Re сначала появляются более крупномасштабные движения, а затем и более мелкие масштабы. При очень больших числах Re – имеют место все масштабы турбулентных пульсаций.

масштабы

Изменение масштабов пульсаций с ростом числа Re

…… все масштабы

Можно определить число Рейнольдса в зависимости от масштабов движения:

масштабами?





Каскадный процесс переноса энергии от больших масштабов к малым (Ричардсон,

1922г.)

Зона генерации
турбулентного движения

Зона диссипации
турбулентного движения

Инерционный интервал

Пусть - среднее количество энергии, диссипируемое в единицу времени в единице массы жидкости. Если ввести изменение средней скорости турбулентного движения
Тогда . В турбулентном режиме удобно ввести не обычную, а так называемую турбулентную вязкость, согласно соотношению:

Откуда:

- таким образом, диссипация энергии турбулентного движения связана со специфической турбулентной вязкостью

имеет место мелкомасштабная турбулентность, которую можно считать однородной и изотропной.

Можно определить масштаб изменения скорости турбулентного движения на расстояниях порядка (величина - скорость турбулентных движений на этих масштабах):

- закон Колмогорова-Обухова

Если ввести вместо длин соответствующие «волновые числа» турбулентных пульсаций , тогда кинетическая энергия (единицы массы жидкости) есть

знаменитый закон «5/3» Колмогорова
(для инерционного интервала)

инерционный интервал