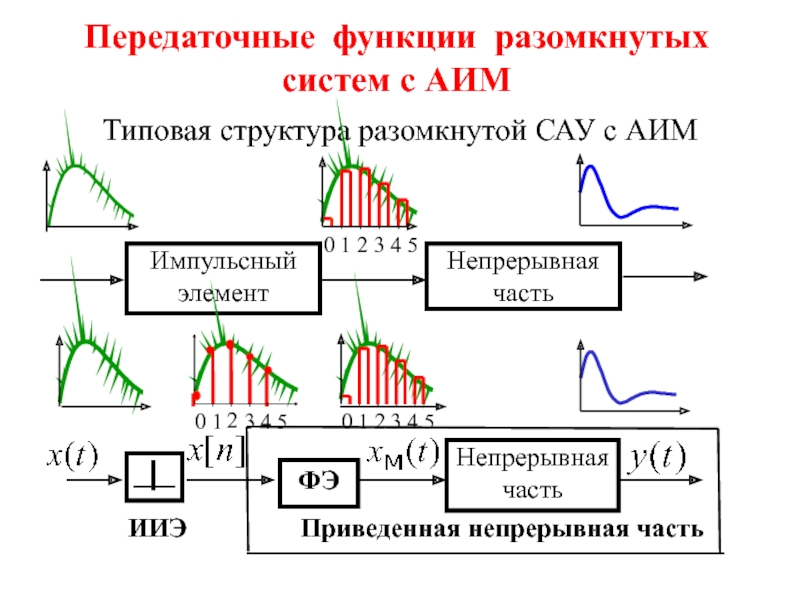
мере один элемент, у которого выходной сигнал является дискретным, называется
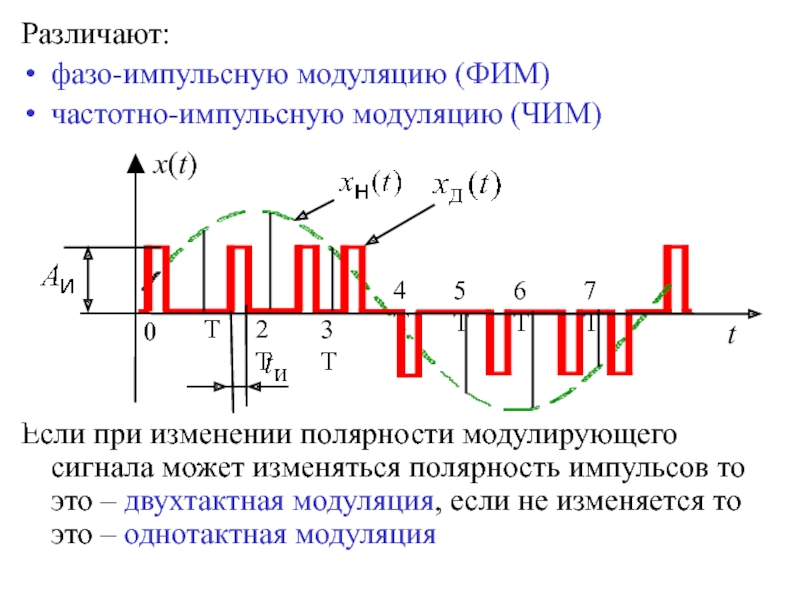
дискретной САУПроцесс преобразования непрерывного сигнала в дискретный называют квантованием сигнала. Различают:
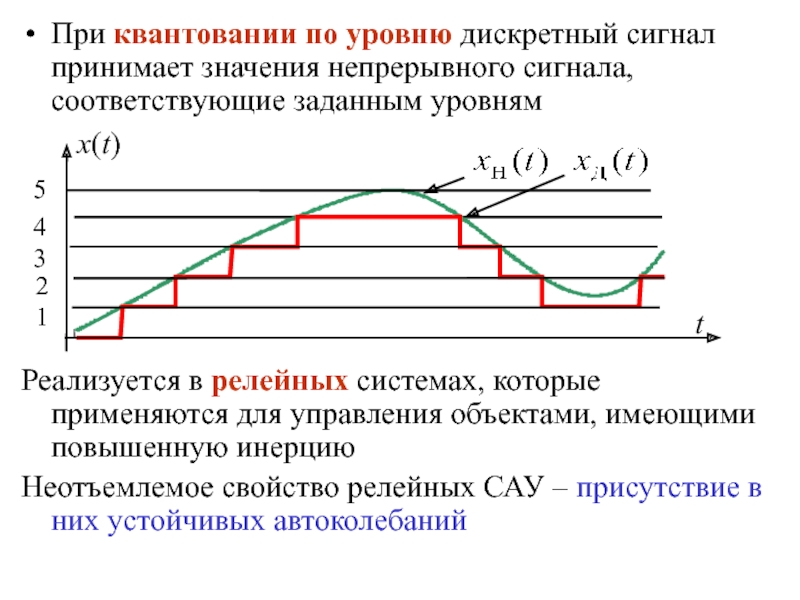
квантование по уровню
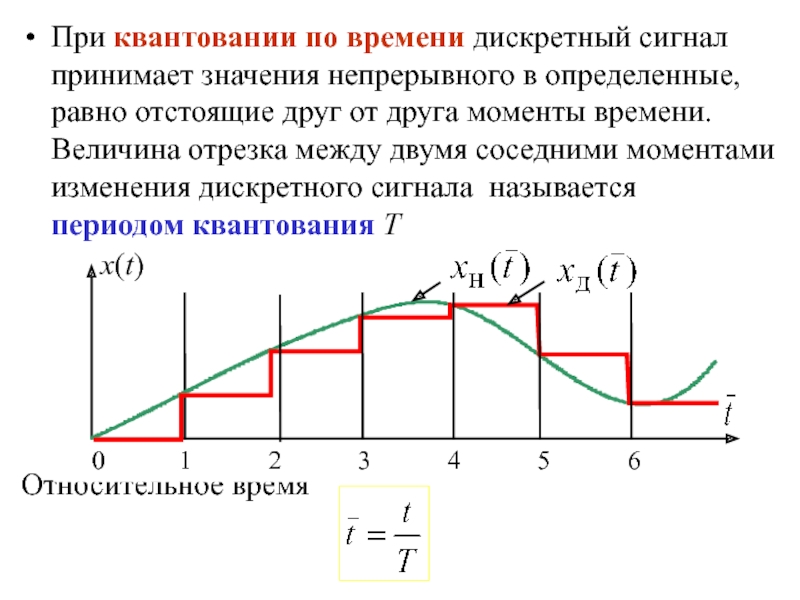
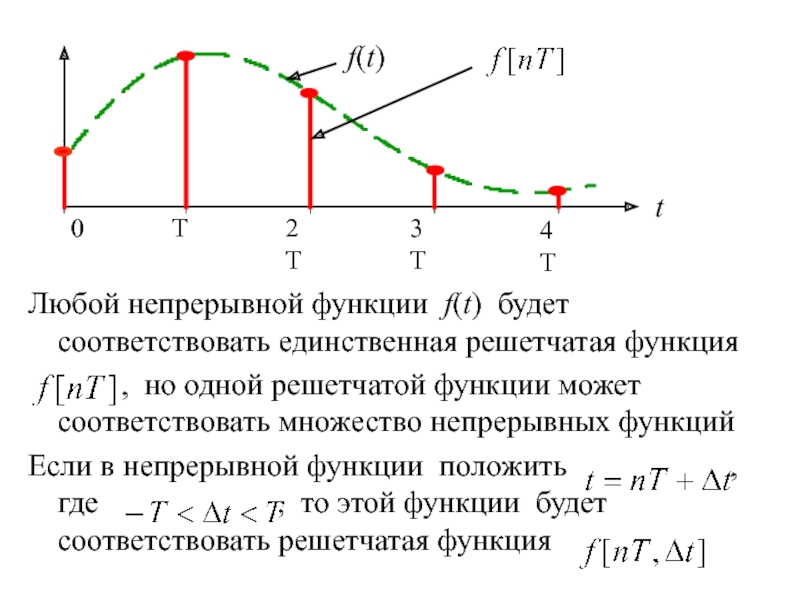
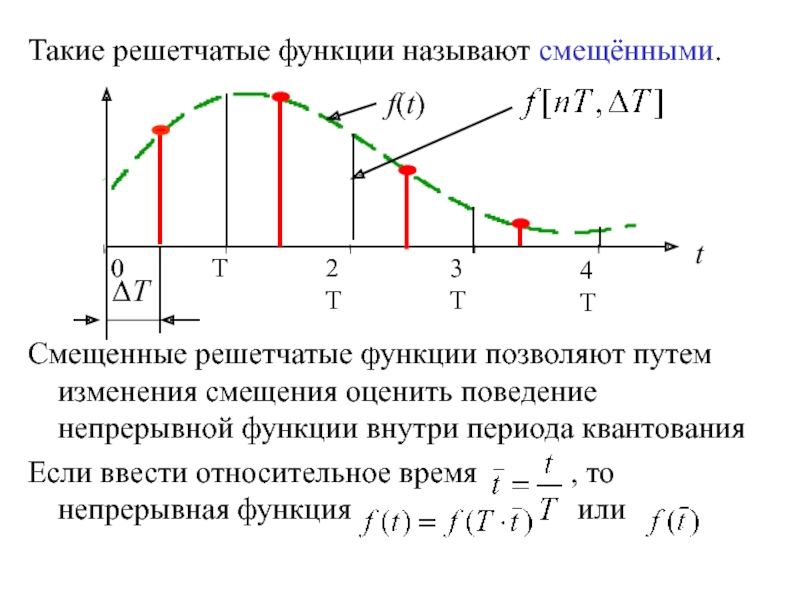
квантование по времени
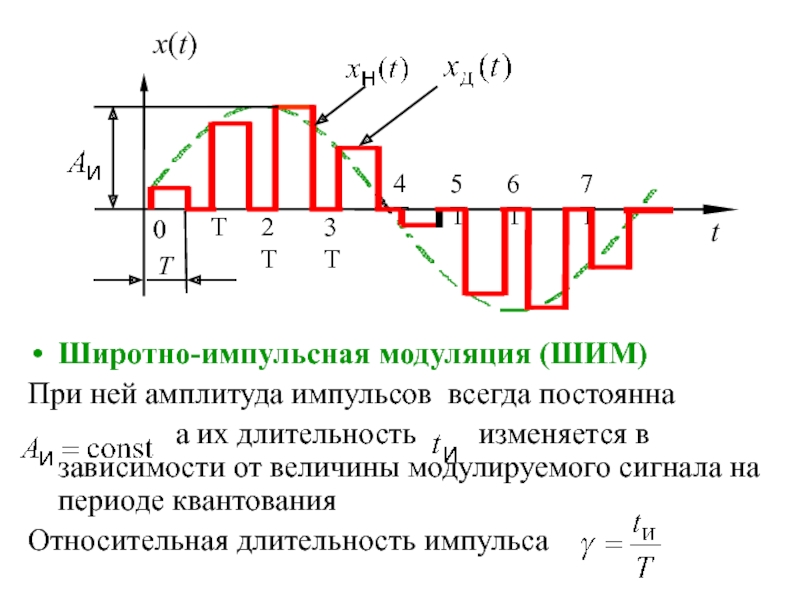
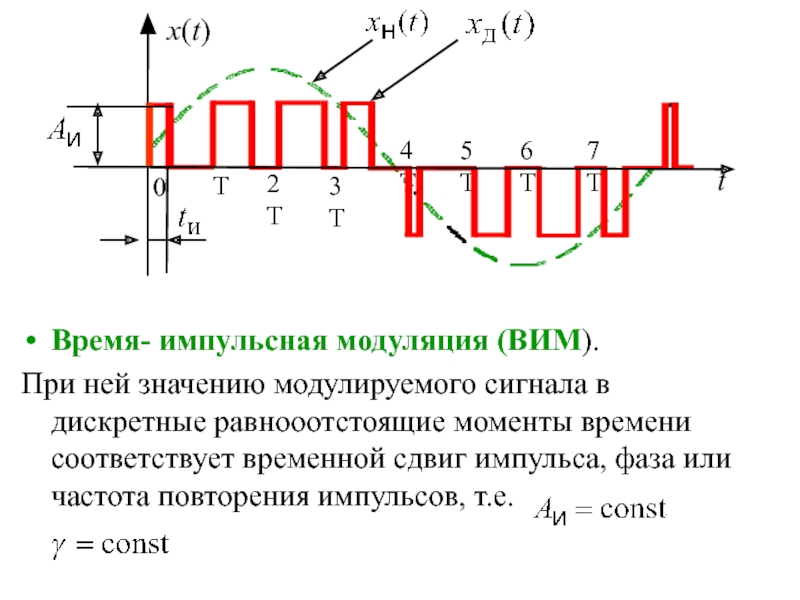
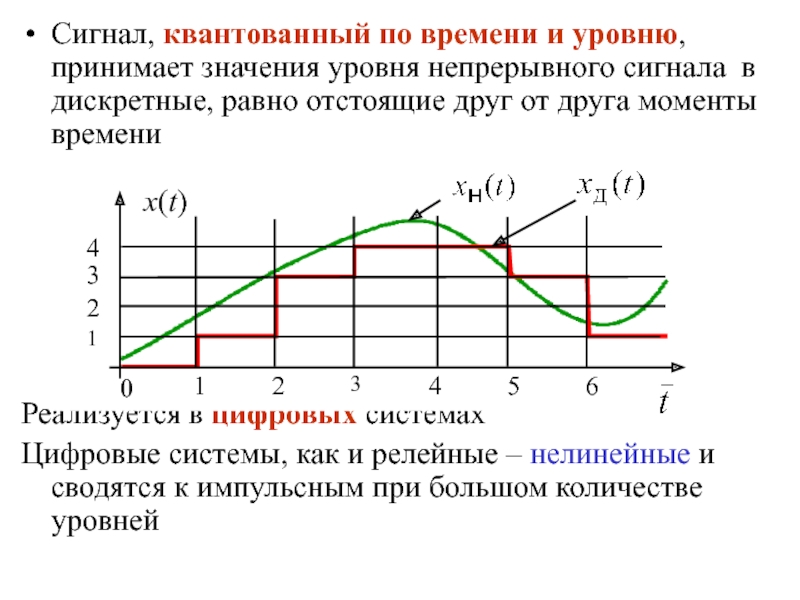
квантование по уровню и времени