Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дискретные системы
Содержание
- 1. Дискретные системы
- 2. Современные микропроцессорыВопросы лекции:Квантование непрерывного сигналаМодель импульсного элемента Особенности сигналов и элементов системы с ЭВМ
- 3. Квантование непрерывного сигналаДискретный элемент – это элемент, преобразующая функция между входом и выходом имеет скачки непрерывности.
- 4. Квантование непрерывного сигналаПри подаче на вход дискретного
- 5. Квантование непрерывного сигналаНа рисунке показан вид дискретного
- 6. Квантование непрерывного сигналаМы будем в основном рассматривать
- 7. Квантование непрерывного сигналаПусть на вход устройства поступает
- 8. Квантование непрерывного сигналаПри квантовании по уровню импульсы
- 9. Квантование непрерывного сигналаПри квантовании и по времени
- 10. Квантование непрерывного сигналаОперации, выполняемые квантователем по времени
- 11. Квантование непрерывного сигналаДля описания работы квантователя по
- 12. Квантование непрерывного сигналаРаботу квантователя и по времени,
- 13. Квантование непрерывного сигналаИз структурных схем преобразователей видно,
- 14. Квантование непрерывного сигналаИмпульсная система автоматического регулирования (САР)
- 15. Модель импульсного элементаРассмотрим импульсную линейную систему. Форма
- 16. Модель импульсного элемента В этом случае, для рассмотрения
- 17. Модель импульсного элемента Вид таких импульсов показан на
- 18. Модель импульсного элемента К такому виду можно привести
- 19. Модель импульсного элемента А по теореме смещения для этих условий мы получим две эквивалентные формулы:
- 20. Модель импульсного элемента То есть при малой ширине
- 21. Модель импульсного элемента Практически это означает, что
- 22. Особенности сигналов и элементов системы с ЭВМПусть
- 23. Особенности сигналов и элементов системы с ЭВМВ
- 24. Особенности сигналов и элементов системы с ЭВМТаким
- 25. Особенности сигналов и элементов системы с ЭВМХотя
- 26. Особенности сигналов и элементов системы с ЭВМПоэтому
- 27. Особенности сигналов и элементов системы с ЭВМПоэтому
- 28. Особенности сигналов и элементов системы с ЭВМСигнал
- 29. Особенности сигналов и элементов системы с ЭВМТаким
- 30. Особенности сигналов и элементов системы с ЭВМПравда,
- 31. Особенности сигналов и элементов системы с ЭВМТаким
- 32. Особенности сигналов и элементов системы с ЭВМЕсли
- 33. Особенности сигналов и элементов системы с ЭВМ
- 34. Особенности сигналов и элементов системы с ЭВМАппарат
- 35. Особенности сигналов и элементов системы с ЭВМ
- 36. Особенности сигналов и элементов системы с ЭВМ
- 37. Особенности сигналов и элементов системы с ЭВМ
- 38. Особенности сигналов и элементов системы с ЭВМ
- 39. Особенности сигналов и элементов системы с ЭВМ
- 40. Особенности сигналов и элементов системы с ЭВМ
- 41. Особенности сигналов и элементов системы с ЭВМПередаточная
- 42. Особенности сигналов и элементов системы с ЭВМЕсли
- 43. Особенности сигналов и элементов системы с ЭВМНапример,
- 44. Особенности сигналов и элементов системы с ЭВМОднако,
- 45. Особенности сигналов и элементов системы с ЭВМПреобразователь
- 46. Особенности сигналов и элементов системы с ЭВМПринцип
- 47. Особенности сигналов и элементов системы с ЭВММетод
- 48. Особенности сигналов и элементов системы с ЭВМУчет
- 49. Особенности сигналов и элементов системы с ЭВМОбщий
- 50. Спасибо за внимание
- 51. Скачать презентанцию
Современные микропроцессорыВопросы лекции:Квантование непрерывного сигналаМодель импульсного элемента Особенности сигналов и элементов системы с ЭВМ
Слайды и текст этой презентации
Слайд 2
Современные микропроцессоры
Вопросы лекции:
Квантование непрерывного сигнала
Модель импульсного элемента
Особенности сигналов и
элементов системы с ЭВМ
Слайд 3
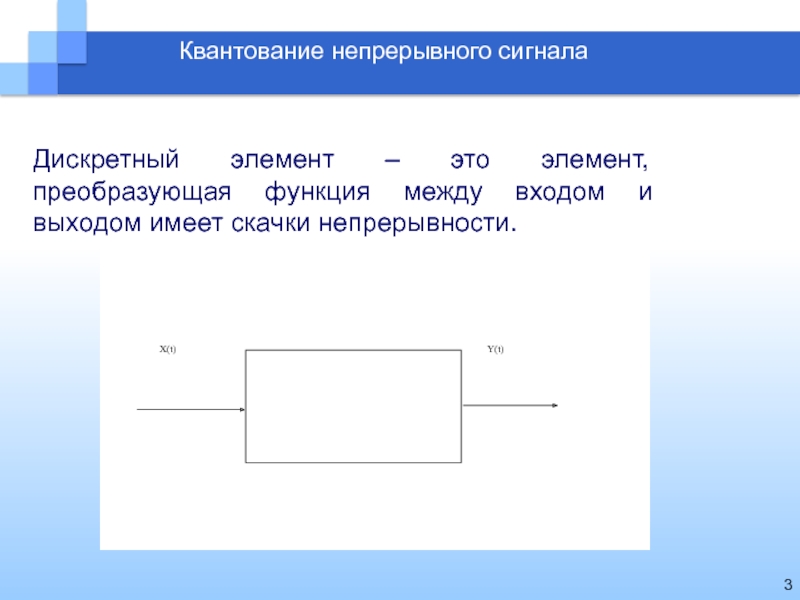
Квантование непрерывного сигнала
Дискретный элемент – это элемент, преобразующая функция между
входом и выходом имеет скачки непрерывности.
Слайд 4
Квантование непрерывного сигнала
При подаче на вход дискретного элемента непрерывного сигнала,
на выходе получается сигнал, изменяющийся скачком – дискретно. Это –
непрерывно-дискретный элемент (Н-Д). Возможен обратный случай, если на входе имеется дискретный сигнал, а на выходе непрерывный - это дискретно-непрерывный элемент (Д-Н).На практике используют дискретные сигналы, имеющие вид импульсов, модулированных по амплитуде – амплитудно-импульсная модуляция (АИМ), по ширине импульсов – широтно-импульсная модуляция (ШИМ) или по частоте импульсов – частотно-импульсная модуляция (ЧИМ).
Слайд 5
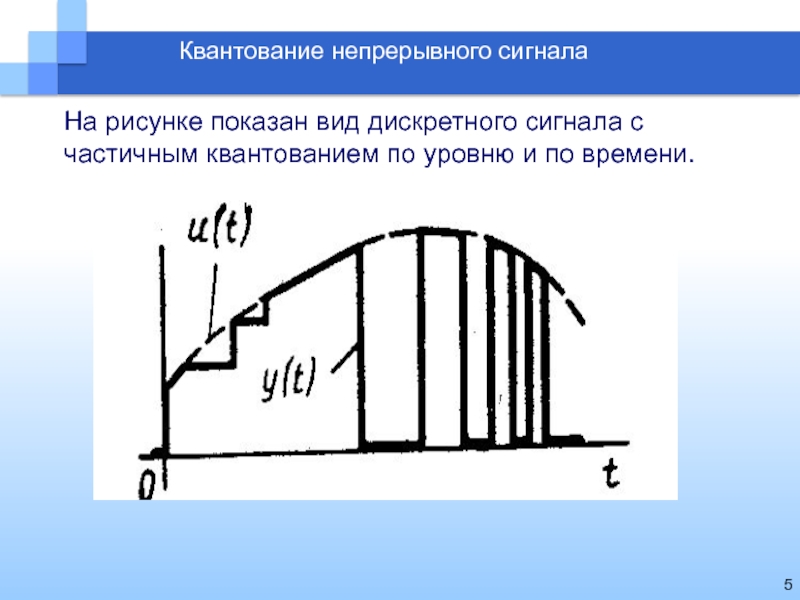
Квантование непрерывного сигнала
На рисунке показан вид дискретного сигнала с частичным
квантованием по уровню и по времени.
Слайд 6
Квантование непрерывного сигнала
Мы будем в основном рассматривать в основном дискретные
сигналы, имеющие вид прямоугольных импульсов с АИМ.
Преобразование непрерывного сигнала
в дискретный называется квантованием. Квантование может быть по уровню, по времени и как по уровню, так и по времени.На рисунке условно показано устройство квантования сигнала.
Слайд 7
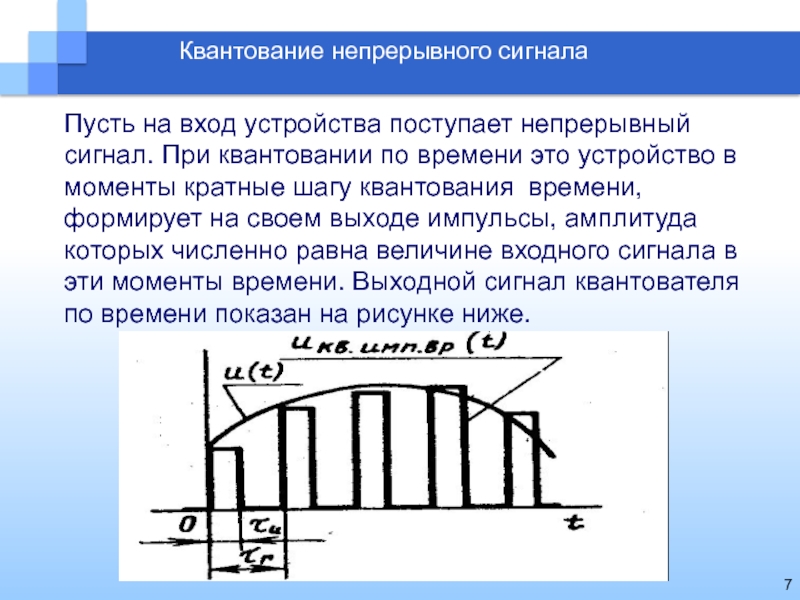
Квантование непрерывного сигнала
Пусть на вход устройства поступает непрерывный сигнал. При
квантовании по времени это устройство в моменты кратные шагу квантования
времени, формирует на своем выходе импульсы, амплитуда которых численно равна величине входного сигнала в эти моменты времени. Выходной сигнал квантователя по времени показан на рисунке ниже.
Слайд 8
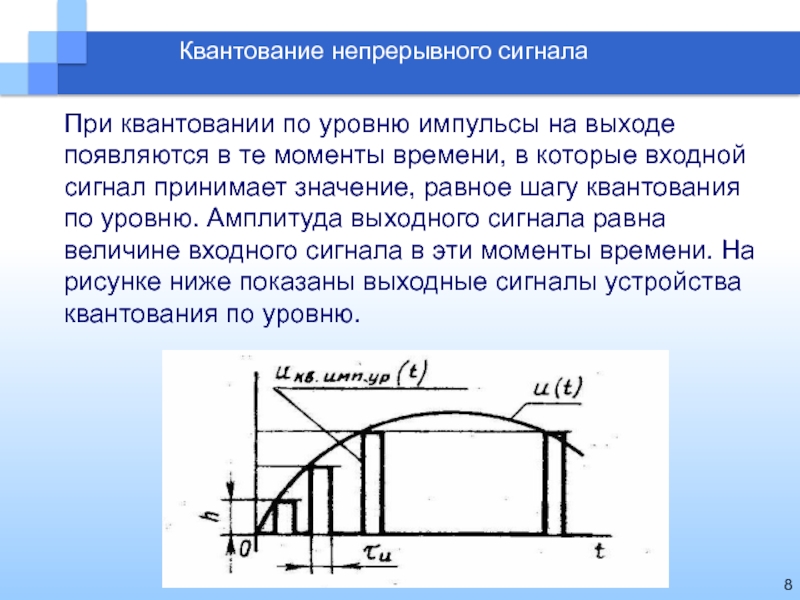
Квантование непрерывного сигнала
При квантовании по уровню импульсы на выходе появляются
в те моменты времени, в которые входной сигнал принимает значение,
равное шагу квантования по уровню. Амплитуда выходного сигнала равна величине входного сигнала в эти моменты времени. На рисунке ниже показаны выходные сигналы устройства квантования по уровню.
Слайд 9
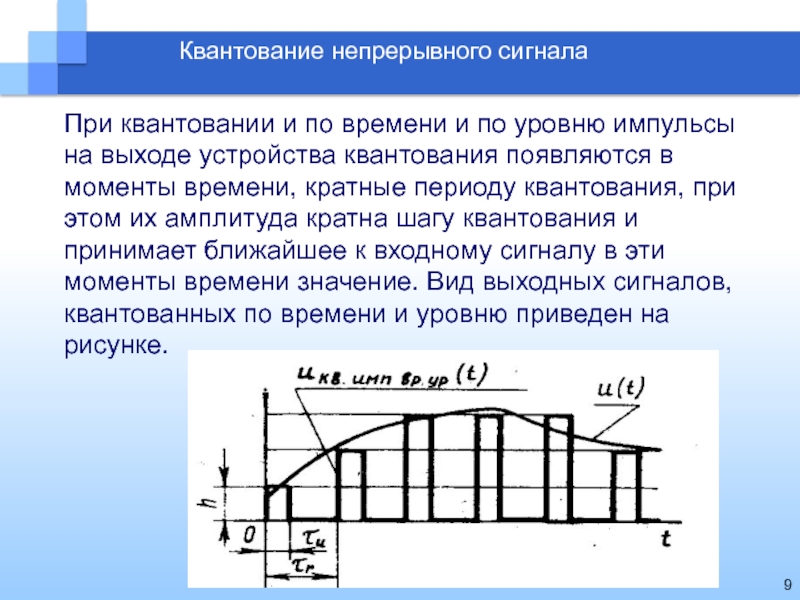
Квантование непрерывного сигнала
При квантовании и по времени и по уровню
импульсы на выходе устройства квантования появляются в моменты времени, кратные
периоду квантования, при этом их амплитуда кратна шагу квантования и принимает ближайшее к входному сигналу в эти моменты времени значение. Вид выходных сигналов, квантованных по времени и уровню приведен на рисунке.
Слайд 10
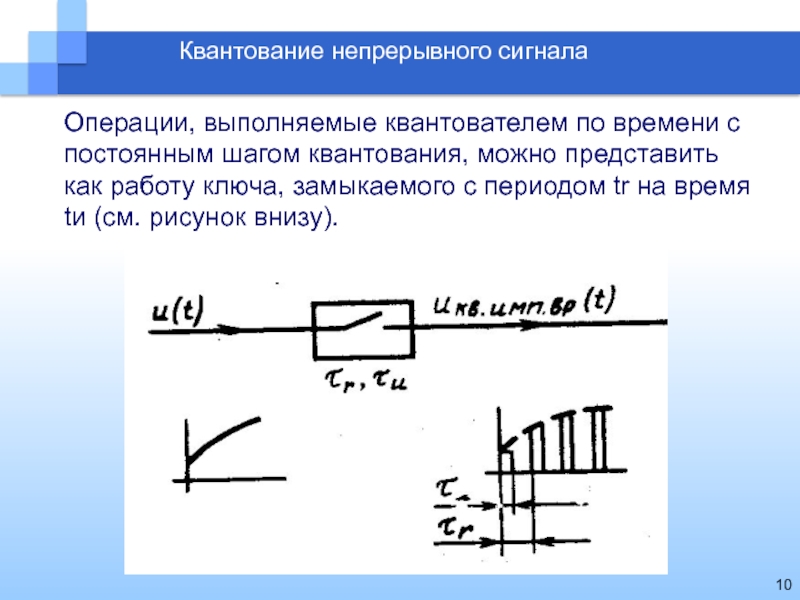
Квантование непрерывного сигнала
Операции, выполняемые квантователем по времени с постоянным шагом
квантования, можно представить как работу ключа, замыкаемого с периодом tr
на время tи (см. рисунок внизу).
Слайд 11
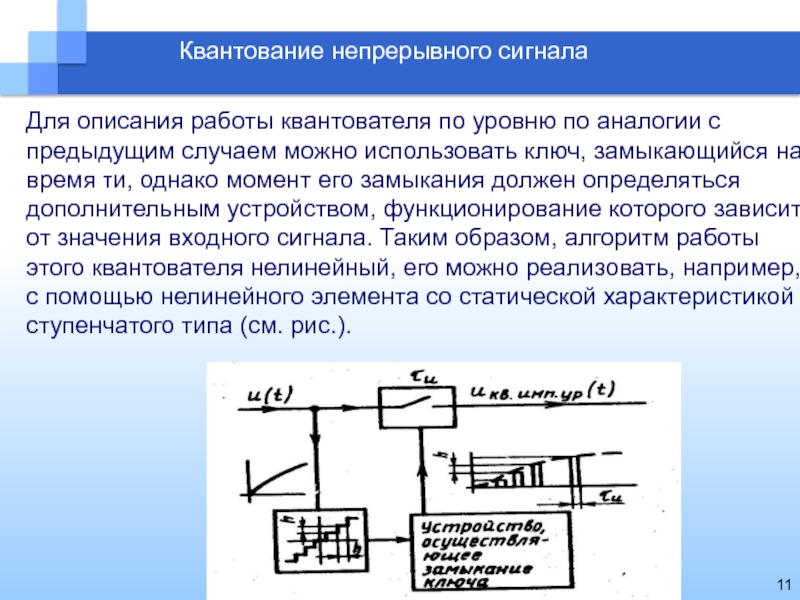
Квантование непрерывного сигнала
Для описания работы квантователя по уровню по аналогии
с предыдущим случаем можно использовать ключ, замыкающийся на время τи,
однако момент его замыкания должен определяться дополнительным устройством, функционирование которого зависит от значения входного сигнала. Таким образом, алгоритм работы этого квантователя нелинейный, его можно реализовать, например, с помощью нелинейного элемента со статической характеристикой ступенчатого типа (см. рис.).
Слайд 12
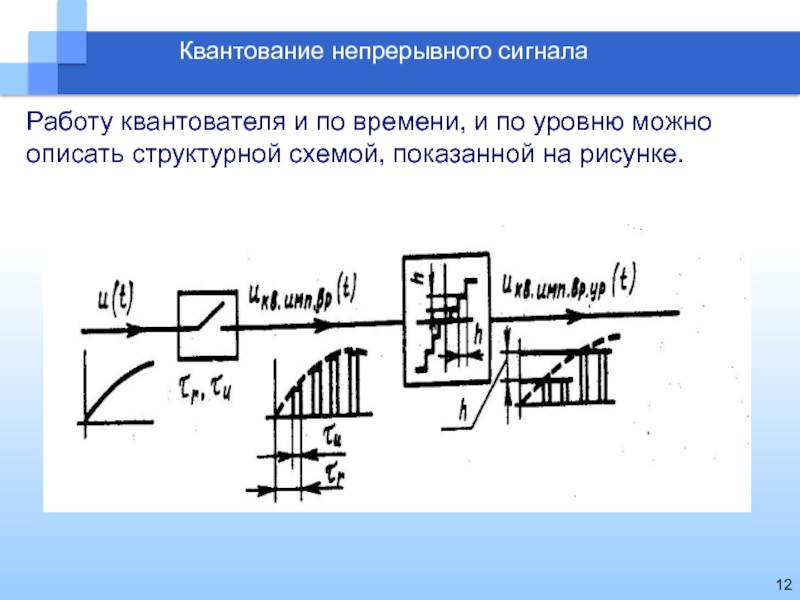
Квантование непрерывного сигнала
Работу квантователя и по времени, и по уровню
можно описать структурной схемой, показанной на рисунке.
Слайд 13
Квантование непрерывного сигнала
Из структурных схем преобразователей видно, что квантование по
уровню связано с дополнительными нелинейными операциями. Поэтому вначале рассмотрим системы
с квантованием только по времени, а учет нелинейных эффектов за счет квантования по уровню будет описан отдельно.
Слайд 14
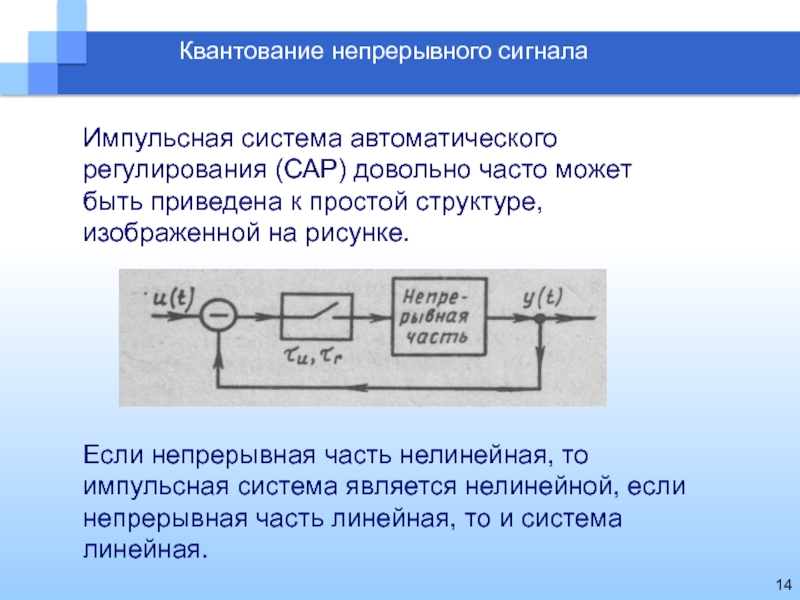
Квантование непрерывного сигнала
Импульсная система автоматического регулирования (САР) довольно часто может
быть приведена к простой структуре, изображенной на рисунке.
Если непрерывная
часть нелинейная, то импульсная система является нелинейной, если непрерывная часть линейная, то и система линейная.
Слайд 15
Модель импульсного элемента
Рассмотрим импульсную линейную систему.
Форма импульсов на входе
импульсного элемента в общем случае оказывает влияние на характер работы
импульсной системы.Однако в случае достаточно узких импульсов, длительность которых гораздо меньше периода и намного меньше постоянной времени передаточной функции W(S) непрерывной части, то результат работы непрерывной части определяется не формой импульса, а его площадью. То есть информация в таком сигнале заключена не в амплитуде импульса, а его площади.
Слайд 16
Модель импульсного элемента
В этом случае, для рассмотрения можно принять любую
форму импульса с такой же площадью. Примем форму импульсов в
виде дельта-функции Дирака, для которой выведены известные закономерности.С помощью дельта функции Дирака сигнал описывается в виде сигнала
Слайд 17
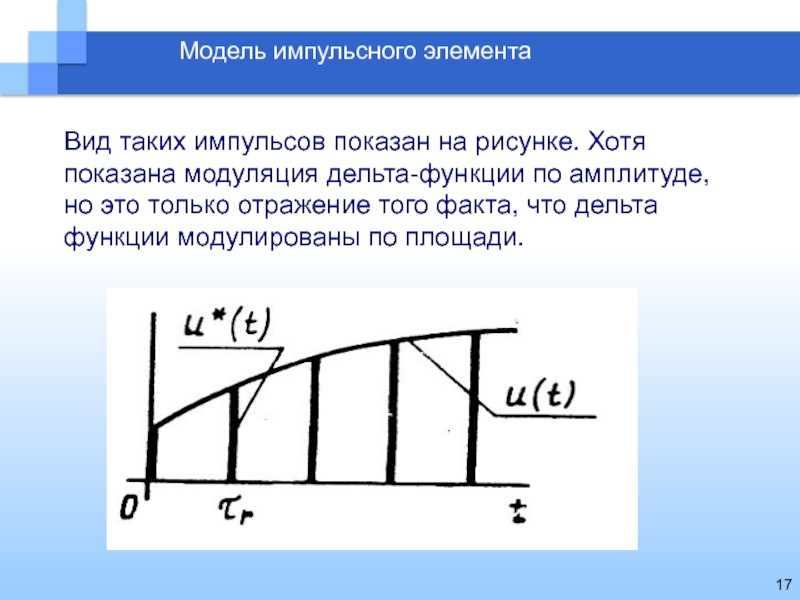
Модель импульсного элемента
Вид таких импульсов показан на рисунке. Хотя показана
модуляция дельта-функции по амплитуде, но это только отражение того факта,
что дельта функции модулированы по площади.
Слайд 18
Модель импульсного элемента
К такому виду можно привести сигналы, установив на
выходе ключа динамическое устройство, формирующую нужную форму импульсов (формирователь импульсов).
Передаточная
функция формирующего устройства должна равняться:WФ1(S) = L [k Ф1 (t) ]
где L – символ, обозначающий операцию преобразования Лапласа.
Слайд 19
Модель импульсного элемента
А по теореме смещения для этих условий мы
получим две эквивалентные формулы:
Слайд 20
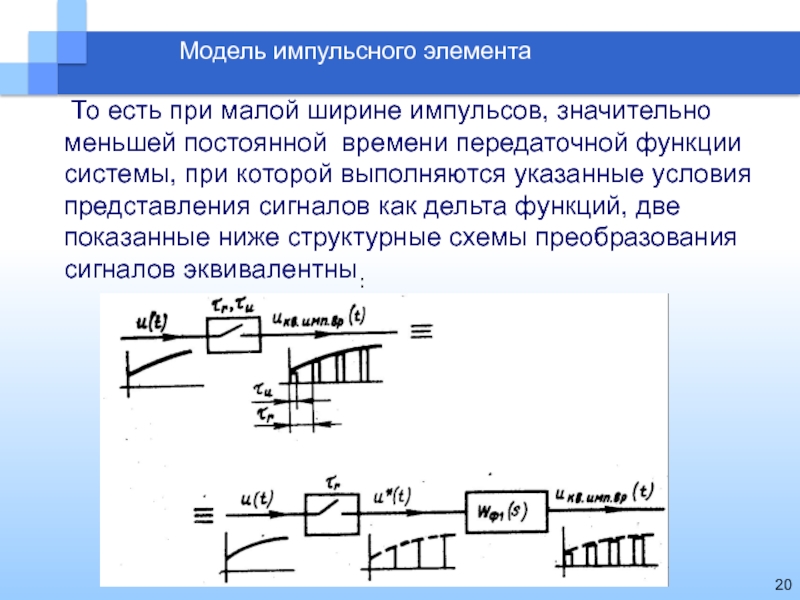
Модель импульсного элемента
То есть при малой ширине импульсов, значительно меньшей
постоянной времени передаточной функции системы, при которой выполняются указанные условия
представления сигналов как дельта функций, две показанные ниже структурные схемы преобразования сигналов эквивалентны:
Слайд 21
Модель импульсного элемента
Практически это означает, что можно реальный импульсный
элемент при условии достаточно узких импульсов представить эквивалентной схемой, дающей
удобное математическое описание.Дополнительно это означает, что последующая после импульсного элемента часть системы реагирует на информацию о работе предыдущей части только в дискретные моменты времени, кратные tr.
Слайд 22
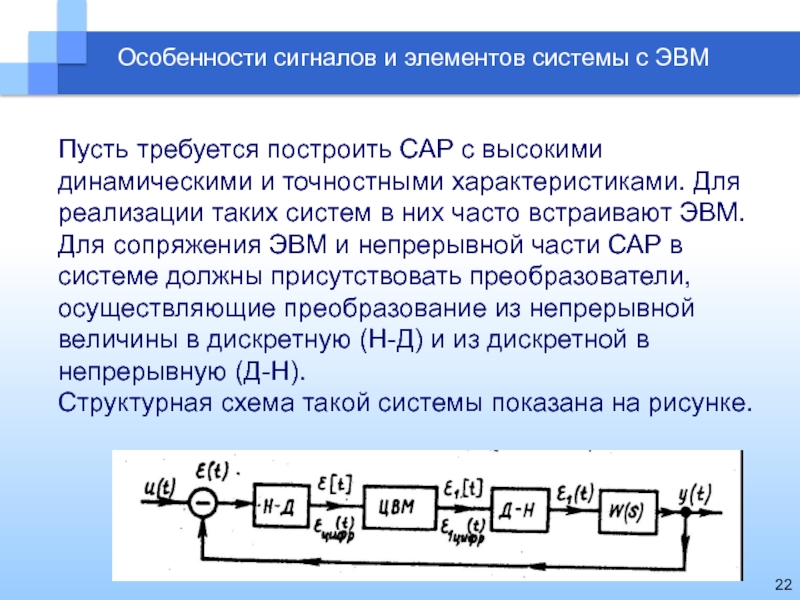
Особенности сигналов и элементов системы с ЭВМ
Пусть требуется построить САР
с высокими динамическими и точностными характеристиками. Для реализации таких систем
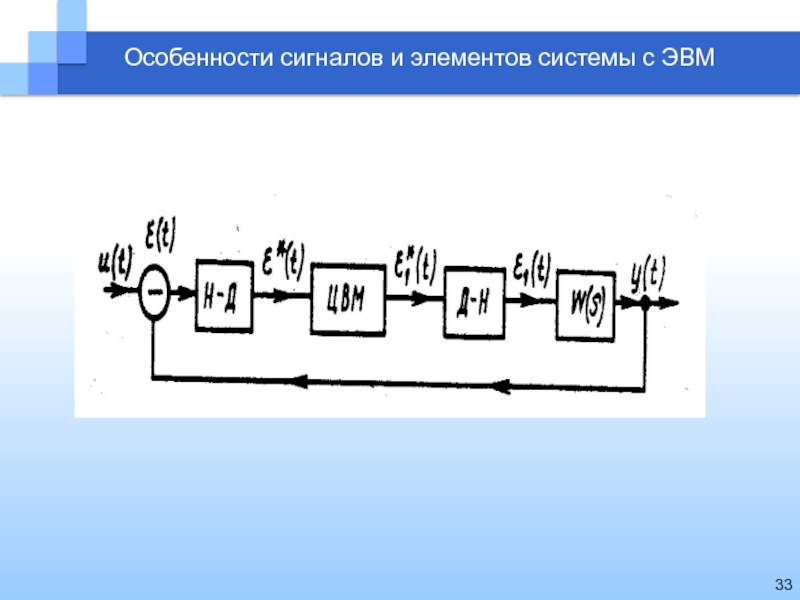
в них часто встраивают ЭВМ.Для сопряжения ЭВМ и непрерывной части САР в системе должны присутствовать преобразователи, осуществляющие преобразование из непрерывной величины в дискретную (Н-Д) и из дискретной в непрерывную (Д-Н).
Структурная схема такой системы показана на рисунке.
Слайд 23
Особенности сигналов и элементов системы с ЭВМ
В системе с цифровой
вычислительной машиной (ЦВМ) имеют место дискретные сигналы другого (в сравнении
с импульсными) типа – цифровые сигналы. Поэтому такая система называется цифровой.В системе с цифровой вычислительной машиной (ЦВМ) имеют место дискретные сигналы другого (в сравнении с импульсными) типа – цифровые сигналы (см. рисунок) εцифр(t), ε1цифр(t). Поэтому такая система называется цифровой.
Слайд 24
Особенности сигналов и элементов системы с ЭВМ
Таким образом, информация в
цифровом сигнале (в отличие от импульсного) заключена в физическом носителе
с помощью кода, - принципиально отличающегося от того, с помощью которого она должна была бы быть заключена во входном сигнале последующего непрерывного элемента.
Слайд 25
Особенности сигналов и элементов системы с ЭВМ
Хотя вид рисунков сигналов
в виде решетчатой функции и последовательности дельта-функций совпадают, но это
только внешнее совпадение. Сигналы ε1*(t), это сигналы, площади которых равны значениям сигнала e1(f) в моменты времени ntr. Такие импульсы могут непосредственно воздействовать на последующий непрерывный элемент, вызывая при соблюдении условий узости импульсов реакцию, зависящую от заключенной в них информации, в виде взвешенной совокупности импульсной передаточной функции последующего элемента.
Слайд 26
Особенности сигналов и элементов системы с ЭВМ
Поэтому физическая суть такого
сигнала для последнего не существенна, в связи с чем от
реального сигнала переходят к его математической абстракции, удобно передающей только информационное содержание этого сигнала, к решетчатой функции ε1[t] — функции, представляющей собой последовательность дискретных значений сигнала в моменты времени, кратные tr:
Слайд 27
Особенности сигналов и элементов системы с ЭВМ
Поэтому преобразователь Д—Н здесь
иногда может и отсутствовать (импульсная система типа 1).
Правда,
если последующий элемент должен реагировать на информацию, которая заключена в сигнале до импульсного элемента, то на выходе последнего обязательно нужно поставить преобразователь Д — Н, преобразующий сигнал ε1*(t) в ε1(t) (импульсная система типа 2).
Слайд 28
Особенности сигналов и элементов системы с ЭВМ
Сигнал же в виде
решетчатой функции ε1[t] обладает нулевой площадью (а,
следовательно, и нулевой энергией) и непосредственно воздействовать на последующий непрерывный элемент не может, в связи с чем после цифровой части всегда должен присутствовать преобразователь либо Д — H1, преобразующий сигнал ε1[t] в ε1*(t) (цифровая система типа 1), либо Д—Н2, преобразующий сигнал ε1[t] в ε1(t) (цифровая система типа 2).
![Особенности сигналов и элементов системы с ЭВМСигнал же в виде решетчатой функции ε1[t] обладает нулевой](/img/thumbs/ce205665ba8236a3fcaf9cef7845482c-800x.jpg "Дискретные системы Особенности сигналов и элементов системы с ЭВМСигнал же в виде решетчатой")
Слайд 29
Особенности сигналов и элементов системы с ЭВМ
Таким образом, при всем
физическом различии сигналов ε1*(t) и ε1[t] в случае совпадения
их ординат цифровая часть цифровой системы типа 1 (типа 2) с помощью решетчатых функций обеспечивает передачу к своей последующей непрерывной части той же информации, что и импульсная часть импульсной системы типа 1 (типа 2) с помощью импульсных функций к своей. Отсюда следует информационная эквивалентность обеих рассмотренных систем (цифровой системы типа 1(2) и импульсной системы типа 1(2)).
![Особенности сигналов и элементов системы с ЭВМТаким образом, при всем физическом различии сигналов ε1*(t) и ε1[t]](/img/thumbs/c8ab270e396268f0cb078c332f1c5557-800x.jpg "Дискретные системы Особенности сигналов и элементов системы с ЭВМТаким образом, при всем физическом")
Слайд 30
Особенности сигналов и элементов системы с ЭВМ
Правда, ЭВМ помимо квантования
по времени (в ней шаг квантования по времени определяется периодом
смены информации, зависящей, в частности, от быстродействия машины) осуществляет еще и квантование по уровню (шаг квантования по уровню определяется разрядной сеткой, задаваемой числом разрядов вычислителя).
Слайд 31
Особенности сигналов и элементов системы с ЭВМ
Таким образом, ЭВМ нужно
было бы представлять как кодово-импульсное устройство. Но ввиду того, что
при большом числе разрядов ЭВМ эффект от квантования по уровню обычно мал, им в первом приближении пренебрежем и представим микро-ЭВМ как чисто импульсное устройство.
Слайд 32
Особенности сигналов и элементов системы с ЭВМ
Если при этом рассматривать
только линейные алгоритмы обработки информации в микро-ЭВМ, то система с
ЭВМ представляется импульсной линейной моделью (показанной на рисунке ниже), в составе которой можно выделить три типа характерных устройств: непрерывные (устройство с передаточной функцией W(s)), непрерывно-дискретные (преобразователи Н—Д и Д—Н) и чисто импульсные (ЭВМ) устройства.
Слайд 34
Особенности сигналов и элементов системы с ЭВМ
Аппарат и методы исследования
непрерывных устройств хорошо известны. Для ЭВМ как чисто импульсного устройства
со входом ε*(t) и выходом ε1*(t), реализующего линейный алгоритм работы (сложения, вычитания, умножения на известный коэффициент, задержки на конечное время, кратное t), имеется аппарат исследования, основанный на методах, аналогичных применяемым для непрерывных систем.
Слайд 35
Особенности сигналов и элементов системы с ЭВМ
Так для исследования
непрерывных систем передаточную функцию получают с помощью преобразования Лапласа, для
цифровых систем аналогичную роль играет Z-преобразование, которое можно вычислить из обычного преобразования Лапласа, выполнив его над импульсной функцией, в результате получаем дискретное преобразование Лапласа.
Слайд 36
Особенности сигналов и элементов системы с ЭВМ
Заменив в нем
etrs на Z, получим один из вариантов Z-преобразования, служащего для
описания различных функций цифровых элементов.
Слайд 37
Особенности сигналов и элементов системы с ЭВМ
В таблице приведены
примеры соответствия между основной функцией u(t), преобразованием Лапласа U(s), и
Z-преобразованием
Слайд 38
Особенности сигналов и элементов системы с ЭВМ
Подробное рассмотрение связи
между преобразованием Лапласа, дискретным преобразованием Лапласа и Z-преобразованием выходит за
рамки данной лекции. Скажем только, что очень важными для исследования являются свойства преобразования, позволяющие вычислить импульсную функцию системы, зная ееZ-преобразование.
Слайд 39
Особенности сигналов и элементов системы с ЭВМ
Интересной особенностью чисто
импульсных систем является то, что формулы для вычисления общей передаточной
функции соединяемых элементов совпадают с аналогичными формулами из теории непрерывных систем.Это следует из того, что основная формула метода
Z-передаточной функции
Y(z) = W(z)U(z)
по форме аналогична формуле из теории непрерывных систем
Слайд 40
Особенности сигналов и элементов системы с ЭВМ
Рассматривая систему управления
с ЦВМ, необходимо учитывать рассмотренные выше особенности преобразователя Н-Д.
При
этом саму ЦВМ можно рассматривать как чисто импульсный элемент со входом ε*(t) и выходом ε1*(t). Иными словами ЦВМ может быть представлена как некоторое чисто импульсное динамическое устройство – цифровой фильтр (импульсный фильтр).
Слайд 41
Особенности сигналов и элементов системы с ЭВМ
Передаточная функция ЦВМ как
некоторого произвольного цифрового фильтра имеет вид (в Z-форме, то есть
после замены etrs на Z):
Слайд 42
Особенности сигналов и элементов системы с ЭВМ
Если задавать конкретные значения
коэффициентам aυ, bμ, то это конкретизирует операцию, описываемую передаточной функцией.
ЦВМ
может выполнять линейные операции связанные, например, с дифференцированием, интегрированием, сложением и т.п.ЦВМ присуще свойство, которое послужило одной из причин введения ее в контур системы автоматического управления (САУ) – наличие у нее запоминающего устройства. В связи с этим работа ЦВМ может строиться с учетом не только текущих, но и прошлых значений входного сигнала.
Слайд 43
Особенности сигналов и элементов системы с ЭВМ
Например, подставляя соответствующие значения
коэффициентов в приведенную выше формулу, получим передаточную функцию идеального дифференцирующего
элемента:
Слайд 44
Особенности сигналов и элементов системы с ЭВМ
Однако, это соотношение выполняется
только в случае медленно меняющихся сигналов, иначе нужно уменьшать период
дискретизации tr, что вытекает и из временного представления сигналов.Аналогично можно выполнить с помощью ЦВМ можно выполнить многие другие линейные функции.
Слайд 45
Особенности сигналов и элементов системы с ЭВМ
Преобразователь Д-Н должен выполнять
функцию приближенного экстраполятора, преобразующий бесконечный спектр импульсных сигналов в конечный
с тем лучшей точностью, чем выше степень полинома, описывающей функцию экстраполяции.
Слайд 46
Особенности сигналов и элементов системы с ЭВМ
Принцип построения систем автоматического
регулирования с ЦВМ требует выполнения условий устойчивости системы регулирования. Для
дискретных систем разработаны критерии устойчивости, являющиеся Z-аналогами критериев устойчивости Михайлова и Найквиста-Михайлова, на которых мы не будем здесь подробно останавливаться, позволяющие рассчитать коэффициенты преобразования элементов системы для выполнения условий устойчивости.
Слайд 47
Особенности сигналов и элементов системы с ЭВМ
Метод Z-преобразования позволяют по
аналогии с использованием преобразования Лапласа рассчитать характеристики корректирующих звеньев системы
регулирования, позволяющих обеспечить требуемые характеристики системы в целом.
Слайд 48
Особенности сигналов и элементов системы с ЭВМ
Учет квантования по уровню
сигналов в цифровой системе производится методами статистического расчета (например метод
фазовой плоскости), позволяющими оценить вводимую погрешность регулирования за счет квантования уровня. Эти погрешности тем меньше, чем больше разрядность данных, обрабатываемых ЦВМ.
Слайд 49
Особенности сигналов и элементов системы с ЭВМ
Общий вывод состоит в
том, что с помощью ЦВМ можно строить системы регулирования, описание
и расчет которых достаточно разработаны.
