Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дистанционная подготовка к Всероссийской олимпиаде по информатике
Содержание
- 1. Дистанционная подготовка к Всероссийской олимпиаде по информатике
- 2. Занятие 3. Расширенный алгоритм Евклида. Разбор задач
- 3. Расширенный алгоритм ЕвклидаОснован на соотношении Безу: НОД
- 4. Код алгоритма на Pascalvar a,b,d,x,y:Longint; procedure
- 5. Пример
- 6. Задача 1
- 7. Перевод в десятичную систему числа x, записанного в q-ичной
- 8. Представим десятичное число 381 в системе счисления
- 9. Задача 2Два натуральных числа a и b
- 10. Решение задачи 2Для решения задачи понадобится вычислять
- 11. Решение задачи 2: программаfunction NOD(A1,A2:integer):integer; label P4,P6;
- 12. Задача 3Члены классического ряда Фибоначчи вычисляются по
- 13. Решение задачи 3: программаvar Count,ok,Max_Code:integer; n1:longint; Fibo_Code:array[1..50]of
- 14. Решение задачи 3: вычисление числа Фибоначчи с заданным номеромfunction Fibo(X:integer):longint; begin if (X
- 15. Для решения некоторой задачи было необходимо перевести
- 16. Идея решения
- 17. Скачать презентанцию
Занятие 3. Расширенный алгоритм Евклида. Разбор задач
Слайды и текст этой презентации
Слайд 1Дистанционная подготовка к Всероссийской олимпиаде по информатике
Преподаватели:
к.ф.-м.н., заведующий кафедрой ВТиКГ
ДВГУПС, преподаватель программы IT-школа Samsung,
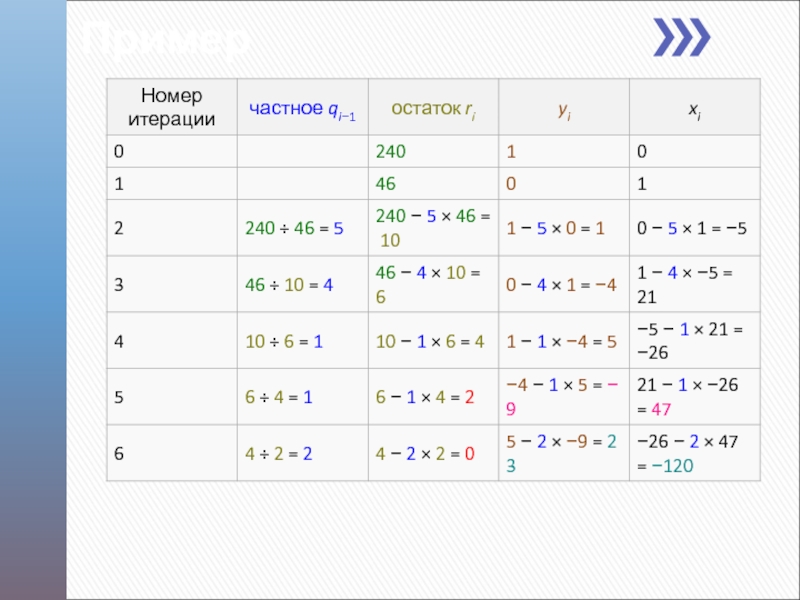
Слайд 3Расширенный алгоритм
Евклида
Основан на соотношении Безу: НОД (a, b) = ax+by,
где
a, b – целые числа,
x, y – коэффициенты Безу
Сложность алгоритма O(log2a)Алгоритм:
НА ВХОДЕ: два неотрицательных числа a и b: a>=b НА ВЫХОДЕ: d=НОД(a,b) и целые x,y: ax + by = d. 1. Если b=0 положить d:=a, x:=1, y:=0 и возвратить (d,x,y)
2. Положить x2:=1, x1:=0, y2:=0, y1:=1 3. Пока b>0 3.1 q:=[a/b], r:=a-qb, x:=x2-qx1, y:=y2-qy1 3.2 a:=b, b:=r, x2:=x1, x1:=x, y2:=y1, y1:=y 4. Положить d:=a, x:=x2, y:=y2 и возвратить (d,x,y)
Слайд 4Код алгоритма на Pascal
var
a,b,d,x,y:Longint;
procedure Eq(a,b:longint; var d,x,y:longint);
var
x1,y1,x2,y2,q,r:Longint;
begin
if b=0 then
begin d:=a; x:=1; y:=0
end
else
begin
x1:=0; x2:=1; y1:=1; y2:=0;
while b>0 do
begin
q:=a div b;
r:=a-q*b;
x:=x2-q*x1;
y:=y2-q*y1;
a:=b; b:=r; x2:=x1; x1:=x; y2:=y1; y1:=y
end;
d:=a; x:=x2; y:=y2
end;
end;
Слайд 7Перевод в десятичную систему числа x, записанного в q-ичной системе счисления в
виде xq=(an an-1…a0 a-1 a-2 … a-m)q,
где ai – цифра соответствующей системы
счисления, находящаяся в позиции i, сводится к вычислению значения многочлена где q – основание системы счисления. В случае отрицательного основания q имеем сумму знакопеременной последовательности – члены с четными степенями положительны, а с нечетными – отрицательны.
Решение задачи 1
Слайд 8Представим десятичное число 381 в системе счисления с основанием q= -2.
Минимальная целая степень, в которую нужно возвести число –2, чтобы
получить число, превосходящее 381, есть 10 ((-2)10 = 1024).Добавим к нему число (-2)9= -512, получим 512. Это больше, чем 381.
Значит, нужно добавить еще отрицательное число, например,
(-2)7= -128, получим 512-128=384.
Результат все еще больше 381, поэтому добавляем еще отрицательное число (-2)3= -8 и получаем 384-8=376, что меньше, чем 381.
Теперь добавим два положительных числа (-2)2 =4 и (-2)0 = 1. Мы получим 376+4+1=381. Значит, можно записать
Решение задачи 1
Слайд 9Задача 2
Два натуральных числа a и b называются взаимно простыми,
если их наибольший общий делитель равен 1.
Несколько натуральных чисел
называются попарно взаимно простыми, если каждое из этих чисел является взаимно простым с каждым другим из них. Например, 10, 11, 21 – попарно взаимно простые числа, а 10, 11, 25 таковыми не являются.
Сколько троек попарно взаимно простых чисел можно составить из двузначных натуральных чисел?
Слайд 10Решение задачи 2
Для решения задачи понадобится вычислять НОД двух чисел.
При этом придется перебирать все возможные тройки двузначных натуральных чисел
и для каждой тройки вычислять НОД для пар чисел, составляющих тройку. Таких НОД для каждой тройки будет три, и если все три НОД равны единице, то составляющие тройку натуральные числа будут взаимно и попарно простыми. Программа, реализующая этот алгоритм, может выглядеть так:
Слайд 11Решение задачи 2: программа
function NOD(A1,A2:integer):integer;
label P4,P6;
var X,Y,Rest:integer;
Begin
X:=A1;Y:=A2;
P4: Rest:=X
mod Y; if Rest=0 then goto P6; X:=Y;Y:=Rest; goto P4;
P6: NOD:=Y; end; var I,J,K,Coprime_N:longint; begin Coprime_N:=0; for I:=10 to 97 do for J:=I+1 to 98 do for K:=J+1 to 99 do if (NOD(I,J)*NOD(J,K)*NOD(I,K))=1 then Coprime_N:= Coprime_N+1; writeln ('Three Coprime Numbers=', Coprime_N); readln; end.Ответ: 34 040 троек
Слайд 12Задача 3
Члены классического ряда Фибоначчи вычисляются по следующему правилу
Начало ряда
выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89, 144, …Любое натуральное число можно представить в виде суммы неповторяющихся чисел Фибоначчи, например:
7=5+2, 20=13+5+2, 33=21+8+3+1 и так далее.
Закодируем натуральное число следующим образом:
если в сумме присутствует число Фибоначчи с номером n, то в соответствующей позиции, начиная справа, ставится единица;
если число Фибоначчи с номером n отсутствует в сумме, в соответствующей позиции ставится ноль, например:
Тогда число 45274 в данной кодировке имеет вид …
Слайд 13Решение задачи 3: программа
var Count,ok,Max_Code:integer;
n1:longint;
Fibo_Code:array[1..50]of integer;
begin
val(paramstr(1),n1,Ok);
write('======',n1,'==>');
for Count:=1
to 50 do Fibo_Code[Count]:=0; Count:=1; while(n1-Fibo(Count)>=0) do Count:=Count+1; Max_code:=Count-1; repeat
Count:=1; while(n1-Fibo(Count)>=0) do Count:=Count+1; Fibo_Code[Count-1]:=1; n1:=n1-Fibo(Count-1); until(n1=0); for Count:=Max_Сode downto 1 do write(Fibo_Code[Count]:1); writeln; readln; end.Слайд 14Решение задачи 3:
вычисление числа Фибоначчи с заданным номером
function Fibo(X:integer):longint;
begin
if
(X
Слайд 15Для решения некоторой задачи было необходимо перевести число
192415363610 в систему счисления
с основанием q.
После успешного решения задачи случился новогодний праздник, в
ходе которого были утеряны результаты решения задачи, результаты преобразования исходного числа в систему счисления с основанием q и само основание системы счисления.В ходе коллективного мозгового штурма удалось вспомнить, что основание системы счисления было натуральным числом, меньшим 100.
Также вспомнилось, что в числе, полученном в результате преобразования исходного числа,
не было нулей и единиц,
содержалось две цифры «2»,
одна цифра «3»,
одна цифра «4»
и не было ни одной цифры «5».
Были там еще какие-то цифры. Но их вспомнить не удалось.
Восстановите основание системы счисления, в которую нужно перевести исходное число .
Задача 4











![Дистанционная подготовка к Всероссийской олимпиаде по информатике Решение задачи 3: программаvar Count,ok,Max_Code:integer; n1:longint; Fibo_Code:array[1..50]of integer; begin val(paramstr(1),n1,Ok); write('======',n1,'==>'); Решение задачи 3: программаvar Count,ok,Max_Code:integer; n1:longint; Fibo_Code:array[1..50]of integer; begin val(paramstr(1),n1,Ok); write('======',n1,'==>'); for Count:=1](/img/thumbs/91039d3e6829ebcae731fda52656842b-800x.jpg)






















