Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дистанционный курс обучения по физике Простые механизмы УРОК №8 Обобщающее
Содержание
- 1. Дистанционный курс обучения по физике Простые механизмы УРОК №8 Обобщающее
- 2. Условия для выполнения работыНа тело должна действовать сила FПод действием этой силы тело должно перемещаться
- 3. Работа - физическая величина, равная произведению силы,
- 4. - физическая величина, которая характеризует результат действия
- 5. МЕХАНИЧЕСКАЯ РАБОТАСИ: [A] = [H ∙ м = Дж]1Дж = 1Н ∙ 1м
- 6. Единицы работы1кДж=1000 Дж1МДж=1000 000Дж1мДж=0,001Дж1мЗа единицу работы принимают
- 7. SSSИтак, если сила и перемещение сонаправлены, то
- 8. Мощность- физическая величина, которая характеризует скорость выполнения работы.МощностьРаботаВремя=N=A / t
- 9. Мощность характеризует быстроту совершения работы.Мощность ( N)
- 10. В Международной системе (СИ) единица мощности называется
- 11. Единицы мощности1кВт=1000 Вт1МВт=1000 000Вт1мВт=0,001Вт1 л.с=736 Вт1мЗа единицу
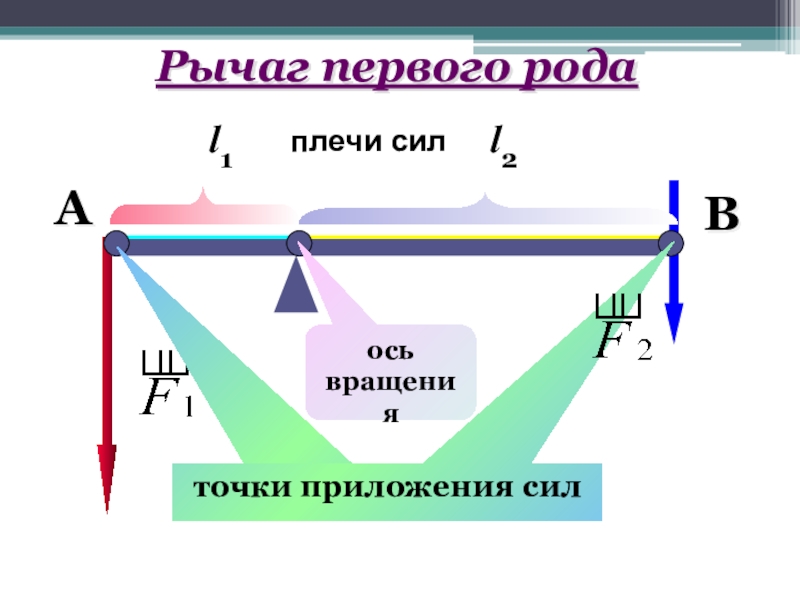
- 12. l1l2АВось вращенияплечи сил Рычаг первого рода
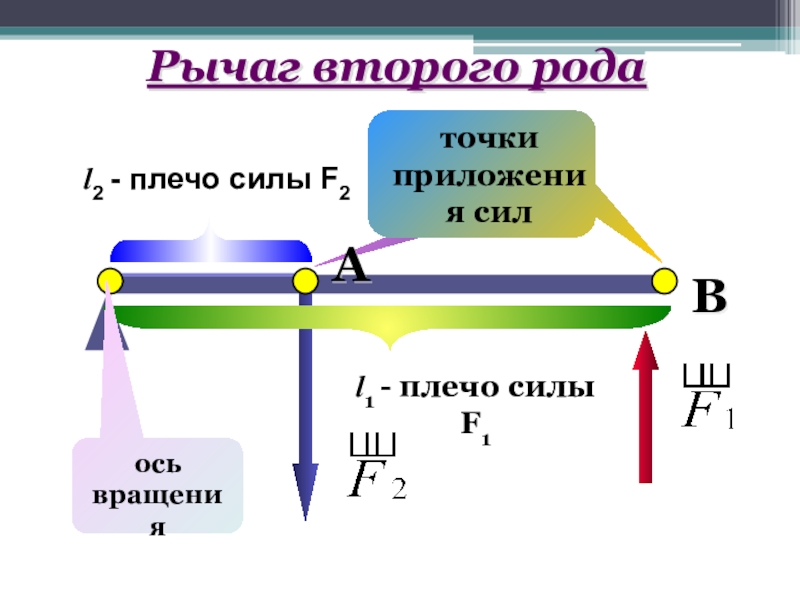
- 13. l1 - плечо силы F1Вl2 - плечо силы F2 Рычаг второго родаось вращенияА
- 14. Плечо силыКратчайшее расстояние между точкой опоры и
- 15. Момент силы Произведение модуля силы, вращающей тело,
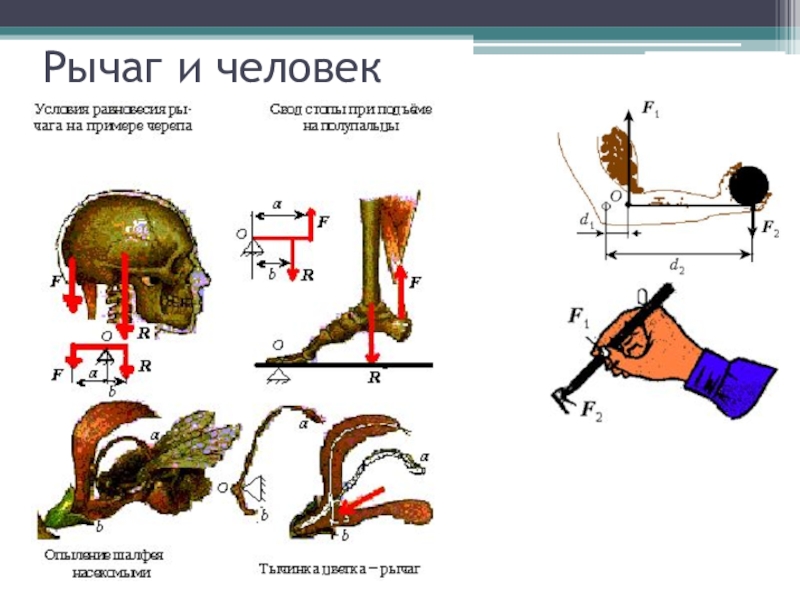
- 16. Рычаг и человек
- 17. Условия равновесия рычагаРычаг находится в равновесии тогда,
- 18. Условия равновесия рычагаРавновесие твердого тела под действием
- 19. Неподвижные блоки Неподвижным блоком называют такой
- 20. Неподвижный блок можно рассматривать как
- 21. Подвижные блоки Подвижный блоки – это блок, ось которого поднимается и опускается вместе с грузом.
- 22. Здесь показан соответствующий ему рычаг:
- 23. Таким образом, подвижный блок даёт выигрыш в силе в 2 раза.
- 24. Комбинируя определенным числом подвижных и неподвижных блоков,
- 25. Простые механизмыНаклонная плоскость применяется для перемещения тяжелых
- 26. Коэффициент полезного действия механизмаТот или иной механизм
- 27. Коэффициент полезного действия механизмаЗатраченная на подъем работа оказывается всегда больше полезной
- 28. Пути повышения КПДуменьшают массу движущихся частей, уменьшают
- 29. ЗОЛОТОЕ правило механикиНи один механизм не дает
- 30. Пример расчета КПДВкатывая бочки массой m по
- 31. Рассмотрим задачи: Подборка заданий по кинематике(из заданий ГИА 2008-2010 гг.)
- 32. ГИА-2010-4. Какой из простых механизмов может дать
- 33. ГИА-2010-4. Рычаг дает выигрыш в силе в
- 34. ЕГЭ-2002 г. А3. На рычаг действуют две
- 35. ЕГЭ-2003 г. А4. На рисунке изображен тонкий
- 36. ЕГЭ-2003 г. А5. Рычаг находится в равновесии
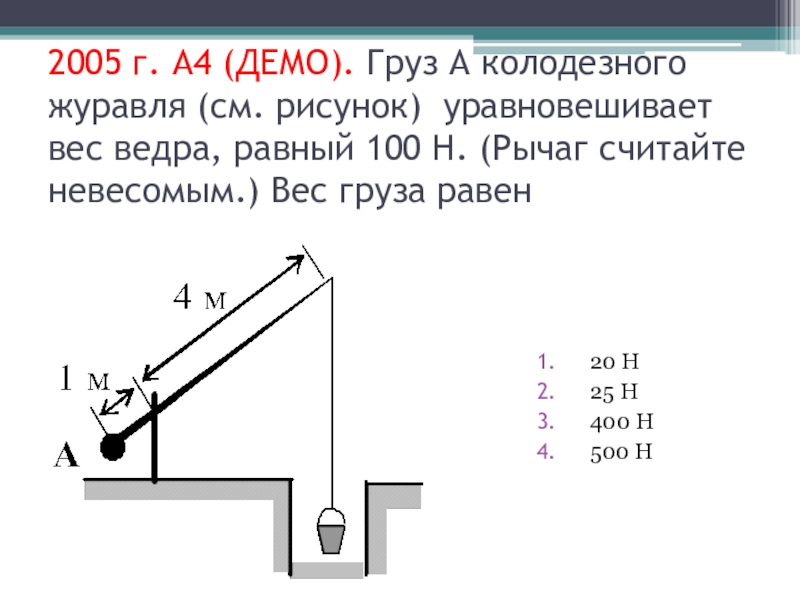
- 37. 2005 г. А4 (ДЕМО). Груз А колодезного
- 38. 2008 г. А5 (ДЕМО). При выполнении лабораторной
- 39. Скачать презентанцию
Условия для выполнения работыНа тело должна действовать сила FПод действием этой силы тело должно перемещаться
Слайды и текст этой презентации
Слайд 1Дистанционный курс обучения по физике «Простые механизмы»
УРОК №8
Обобщающее повторение по
темам «Работа. Мощность. Энергия»
Слайд 2Условия для выполнения работы
На тело должна действовать сила F
Под действием
этой силы тело должно перемещаться
Слайд 3Работа - физическая величина, равная произведению силы, действующей на тело,
на путь, совершенный телом под действием силы в направлении этой
силы.А = F · s
А - механическая работа,
F - сила,
S - пройдённый путь.
Слайд 4- физическая величина, которая характеризует результат действия силы.
А - механическая
работа,
F - сила,
S - пройденный путь.
МЕХАНИЧЕСКАЯ РАБОТА
![МЕХАНИЧЕСКАЯ РАБОТАСИ: [A] = [H ∙ м = Дж]1Дж = 1Н ∙ 1м](/img/thumbs/82bc35a931ff4dbab00a58bd709ee042-800x.jpg "Дистанционный курс обучения по физике Простые механизмы
УРОК №8
Обобщающее МЕХАНИЧЕСКАЯ РАБОТАСИ: [A] = [H ∙ м = Дж]1Дж = 1Н ∙ 1м")
Слайд 6Единицы работы
1кДж=1000 Дж
1МДж=1000 000Дж
1мДж=0,001Дж
1м
За единицу работы принимают работу, совершаемую силой
в 1 Н, на пути, равном 1 м.
Измеряют в Джоулях
А
= 1 Дж=1Н·1м
Слайд 7S
S
S
Итак, если сила и перемещение сонаправлены, то совершается положительная работа!
Если
сила и перемещение перпендикулярны друг другу, то работа не совершается!
Если
сила и перемещение противоположно направлены, то совершается отрицательная работа!
Слайд 8Мощность
- физическая величина, которая характеризует скорость выполнения работы.
Мощность
Работа
Время
=
N=A / t
Слайд 9Мощность характеризует быстроту совершения работы.
Мощность ( N) – физическая величина,
равная отношению работы A к промежутку времени t, в течение
которого совершена эта работа.Мощность показывает, какая работа совершается за единицу времени.
Слайд 10В Международной системе (СИ) единица мощности называется Ватт (Вт) в
честь английскогоизобретателя Джеймса Ватта ( Уатта ), построившего первую паровую
машину.[ N ] = Вт = Дж / c
1 Вт = 1 Дж / 1с
1 Ватт равен мощности силы, совершающей работу в 1 Дж за 1 секунду
Слайд 11Единицы мощности
1кВт=1000 Вт
1МВт=1000 000Вт
1мВт=0,001Вт
1 л.с=736 Вт
1м
За единицу мощности принимают работу,
совершаемую силой в 1 Дж, за 1 секунду.
Измеряют в Ваттах
N
= 1 Вт=1Дж/1с1л.с. = 735 Вт
Слайд 14Плечо силы
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой
действует на рычаг сила, называется плечом силы.
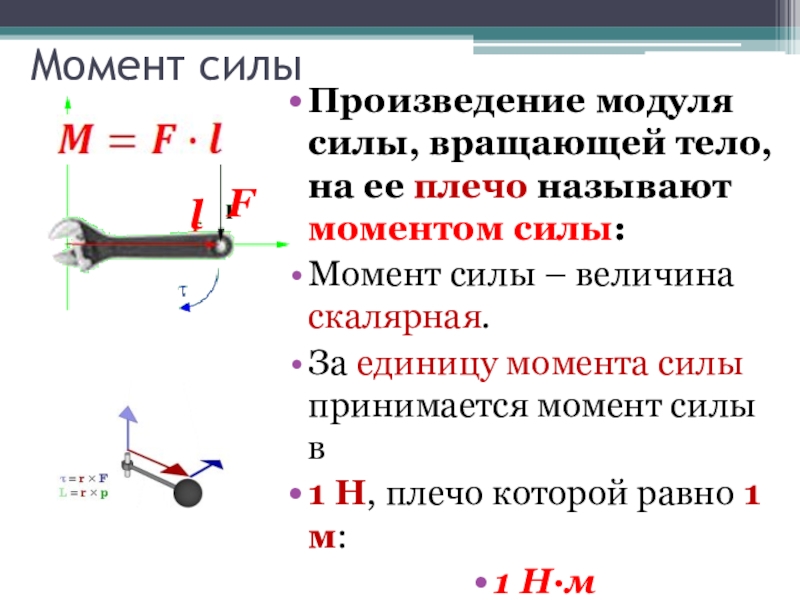
Слайд 15Момент силы
Произведение модуля силы, вращающей тело, на ее плечо
называют моментом силы:
Момент силы – величина скалярная.
За единицу момента силы
принимается момент силы в 1 Н, плечо которой равно 1 м:
1 Н·м
F
l
Слайд 17Условия равновесия рычага
Рычаг находится в равновесии тогда, когда силы, действующие
на него, обратно пропорциональны плечам этих сил
l2 = 2
F2 =
3l1 = 3
F1 = 2
Это правило было установлено Архимедом. По легенде, он воскликнул:
«Дайте мне точку опоры, и я подниму Землю»
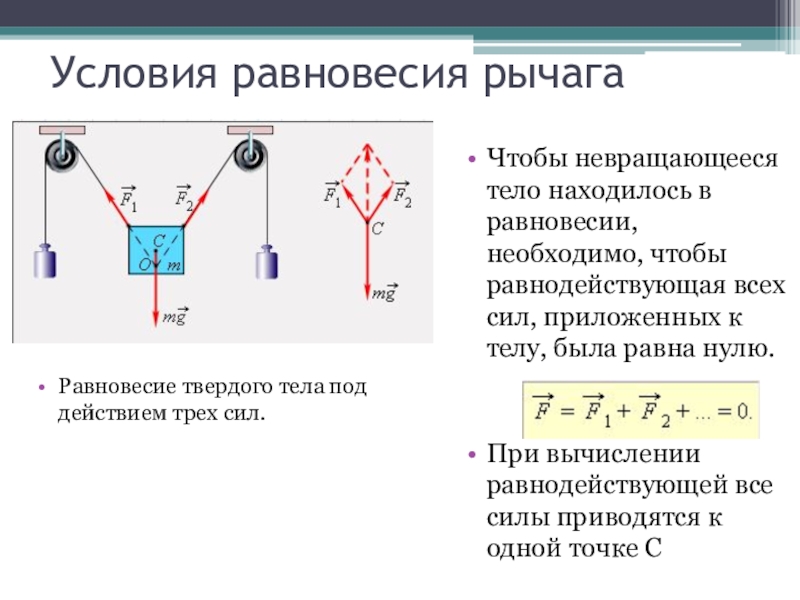
Слайд 18Условия равновесия рычага
Равновесие твердого тела под действием трех сил.
Чтобы
невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил,
приложенных к телу, была равна нулю.При вычислении равнодействующей все силы приводятся к одной точке C
Слайд 19Неподвижные блоки
Неподвижным блоком называют такой блок, ось которого
закреплена и при подъёме грузов не поднимается и не опускается.
Слайд 20 Неподвижный блок можно рассматривать как равноплечий рычаг, у
которого плечи сил равны радиусу колёса: OA=OB=r. Такой блок не
дает выигрыша в силе (F1=F2), но позволяет менять направление действия силы.
Слайд 21Подвижные блоки
Подвижный блоки – это блок, ось которого
поднимается и опускается вместе с грузом.
Слайд 22 Здесь показан соответствующий ему рычаг: O – точка
опоры рычага, ОА плечо силы P и ОВ – плечо
силы F. Так как плечо ОВ в 2 раза больше плеча ОА, то сила F в 2 раза меньше силы Р.
Слайд 24Комбинируя определенным числом подвижных и неподвижных блоков, можно получить значительный
выигрыш в силе
Неподвижный блок
Подвижный блок
Выигрыш силе в 2 раза
Неподвижные блоки
Подвижные
блокиВыигрыш силе в 4 раза
Если есть простейший полиспаст — сочетание группы подвижных и неподвижных блоков, то выигрыш в силе тяги — четный, а в более сложных конструкциях — произвольный
Слайд 25Простые механизмы
Наклонная плоскость применяется для перемещения тяжелых предметов на более
высокий уровень без их непосредственного поднятия.
пандусы,
эскалаторы,
обычные лестницы,
конвейеры.
Если нужно
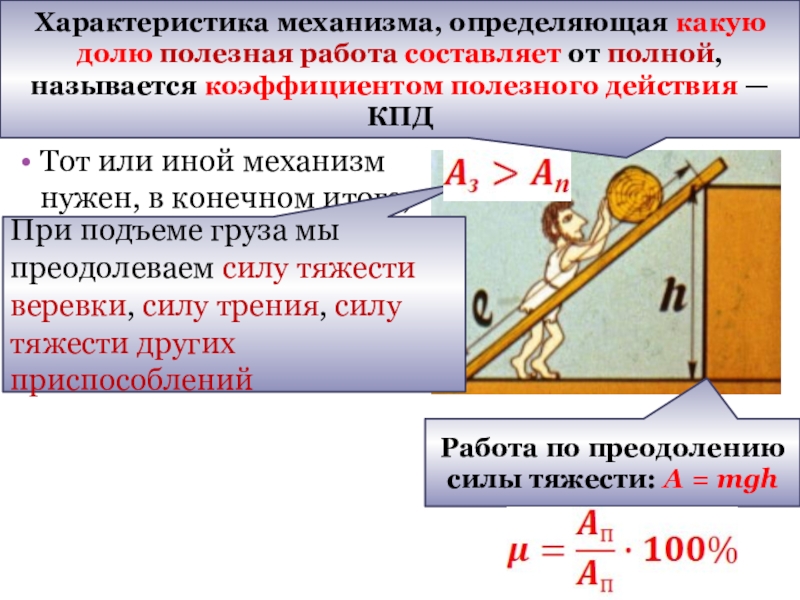
поднять груз на высоту, всегда легче воспользоваться пологим подъемом, чем крутым: чем положе уклон, тем легче выполнить эту работу. 
Слайд 26Коэффициент полезного действия механизма
Тот или иной механизм нужен, в конечном
итоге, для совершения работы.
Полезная работа Ап - необходимая нам работа.
Работа
по преодолению силы тяжести: A = mghПри подъеме груза мы преодолеваем силу тяжести веревки, силу трения, силу тяжести других приспособлений
Характеристика механизма, определяющая какую долю полезная работа составляет от полной, называется коэффициентом полезного действия — КПД
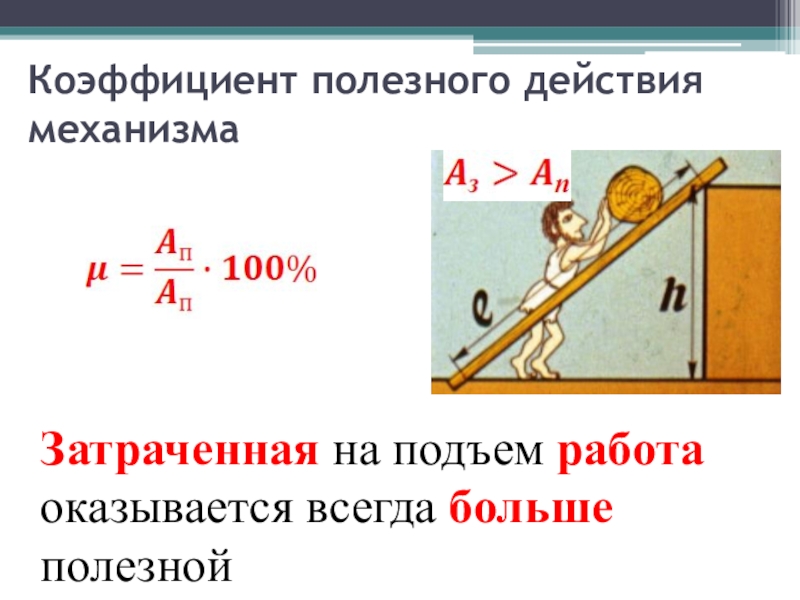
Слайд 27Коэффициент полезного действия механизма
Затраченная на подъем работа оказывается всегда больше
полезной
Слайд 28Пути повышения КПД
уменьшают массу движущихся частей,
уменьшают трение в деталях.
Созданы
машины и механизмы, у которых КПД достигает 98-99%.
Построить машину с
КПД равным 100% невозможно, можно лишь достичь условия, что Ап ≈ Аз
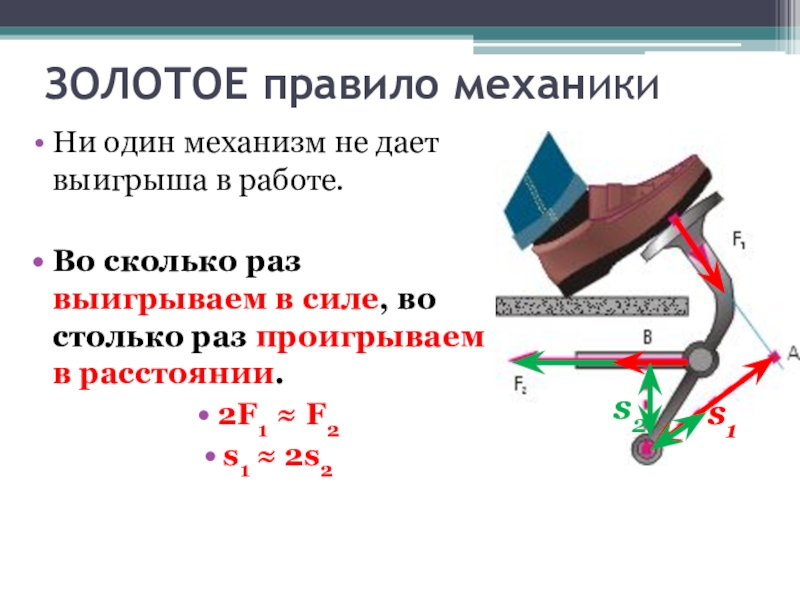
Слайд 29ЗОЛОТОЕ правило механики
Ни один механизм не дает выигрыша в работе.
Во сколько раз выигрываем в силе, во столько раз проигрываем
в расстоянии.2F1 ≈ F2
s1 ≈ 2s2
s1
s2
Слайд 30Пример расчета КПД
Вкатывая бочки массой m по наклонной плоскости длиной
L, человек прикладывают силу F. Высота плоскости – h.
Работа полезная:
Ап
= mgh Работа затраченная:
Aз = F∙L
КПД
Слайд 32ГИА-2010-4. Какой из простых механизмов может дать больший выигрыш в
работе — рычаг, наклонная плоскость или подвижный блок?
1) рычаг
2) наклонная
плоскость3) подвижный блок
4) ни один простой механизм ни дает выигрыша в работе
Слайд 33ГИА-2010-4. Рычаг дает выигрыш в силе в 5 раз. Каков
при этом выигрыш или проигрыш в расстоянии?
выигрыш в 5 раз
нет
ни выигрыша, ни проигрышапроигрыш в 5 раз
выигрыш или проигрыш в зависимости от скорости движения
Слайд 34ЕГЭ-2002 г. А3. На рычаг действуют две силы, плечи которых
равны 0,1 м и 0,3 м. Сила, действующая на короткое
плечо, равна 3 Н. Чему должна быть равна сила, действующая на длинное плечо, чтобы рычаг был в равновесии?1 Н
6 Н
9 Н
12 Н
F1 · d1 = F2 · d2
3 Н · 0,1 м = F2 · 0,3 м
Слайд 35ЕГЭ-2003 г. А4. На рисунке изображен тонкий невесомый стержень, к
которому в точках 1 и 3 приложены силы F1 =
100 Н и F2 = 300 Н. В какой точке надо расположить ось вращения, чтобы стержень находился в равновесии? Ось вращения закреплена.2
6
4
5
Слайд 36ЕГЭ-2003 г. А5. Рычаг находится в равновесии под действием двух
сил. Сила F1 = 4 H. Какова сила F2, если
плечо силы F1 равно 15 см, а плечо силы F2 равно 10 см?4 Н
0,16 Н
6 Н
2,7 Н
Слайд 372005 г. А4 (ДЕМО). Груз А колодезного журавля (см. рисунок)
уравновешивает вес ведра, равный 100 Н. (Рычаг считайте невесомым.) Вес
груза равен20 Н
25 Н
400 Н
500 Н
Слайд 382008 г. А5 (ДЕМО). При выполнении лабораторной работы ученик установил
наклонную плоскость под углом 60 к поверхности стола. Длина плоскости
равна 0,6 м. Момент силы тяжести бруска массой 0,1 кг относительно точки О при прохождении им середины наклонной плоскости равен0,15 Нм
0,30 Нм
0,45 Нм
0,60 Нм
