Слайд 1Дисциплина «Управление производством и услугами»
тема Сетевое планирование
Слайд 2Построение сетевого графика
Системой сетевого планирования и управления называется система
организационного управления, реализующая функции: планирования, контроля и оперативного управления комплексами
работ на основе построения, анализа, оптимизации и актуализации особого класса экономико-математических моделей, называемых сетевыми моделями (сетевыми графиками). Одним из видов сетевого планирования и управления является моделирование на основе PERT-сетей.
Будем рассматривать одно-целевую сетевую модель (сетевой график) небольшого объема (25-30 событий) в терминах работ (стрелки) и событий (кружки) с детерминированной структурой и смешанной оценкой длительности работ (детерминированной и вероятностной).
Сетевым графиком называется графическое изображение комплекса работ в виде ориентированного графа без контуров с дугами (работами), имеющими одну или несколько числовых характеристик, отображающими взаимосвязь между событиями.
Слайд 3Построение сетевого графика
Основные элементы сетевого графика: работы и события.
Работа –
это процесс, происходящий во времени, поэтому можно говорить об объеме
работы, выполненным к моменту времени.
В системе PERT существует несколько значений термина «работа»:
1. действительная работа – или просто работа, т.е. производственный или творческий процесс, требующий затрат труда, времени и материальных ресурсов.
2. ожидание – процесс, требующий только затрат времени (без привлечения каких-либо ресурсов).
3. зависимость (фиктивная работа) – работа, не требующая затрат труда, времени и ресурсов.
Действительную работу и ожидание на сетевом графике принято обозначать сплошной стрелкой, а зависимость – пунктирной.
Слайд 4Построение сетевого графика
Событие означает определенное состояние в процессе выполнения работ,
т.е. событие – это определенный результат предшествующих работ, дающий возможность
начать другие работы. Событие обычно обозначается кружком.
Предшествующее событие – это событие, которое определяет начало работы.
Последующее событие – это событие, которое определяет завершение работы.
Исходным (или начальным) называется событие, которое не имеет непосредственно предшествующих ему работ.
Конечным (или завершающим) называется событие, которое не имеет непосредственно следующих за ним работ.
Слайд 5Построение сетевого графика
Любая последовательность работ в сетевом графике, в которой
конечное событие каждой работы совпадает с начальным событием следующей за
ней работы, называется путем.
Путь сетевого графика, имеющий начало в исходном событии, а конец в завершающем, называется полным путем.
Путь, обладающий максимальной длительностью из всех имеющихся полных путей, называется критическим. Критический путь показывает время необходимое для выполнения всего комплекса работ.
Слайд 6
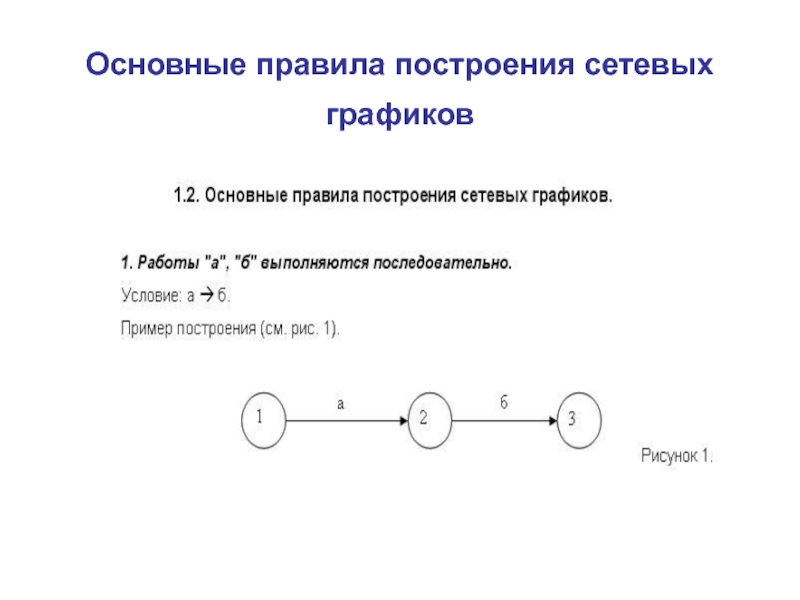
Основные правила построения сетевых графиков
Слайд 7Основные правила построения сетевых графиков
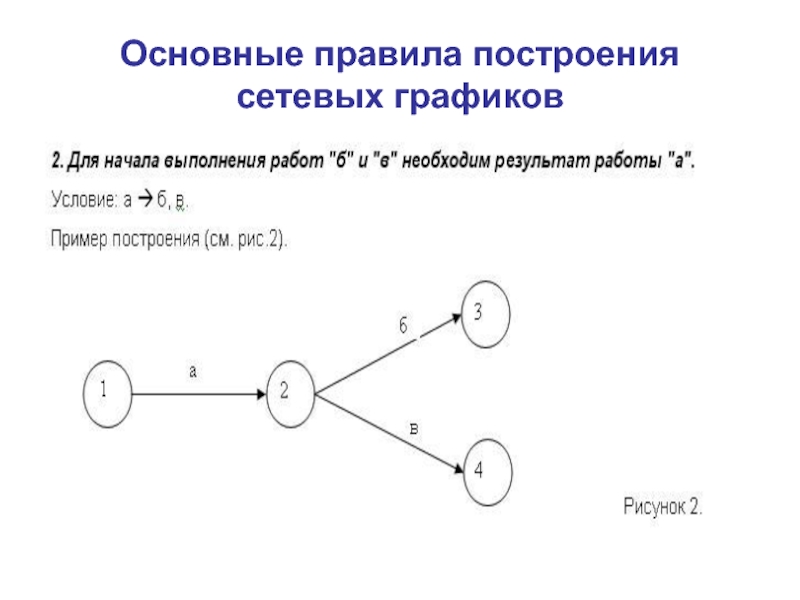
Слайд 8Основные правила построения сетевых графиков
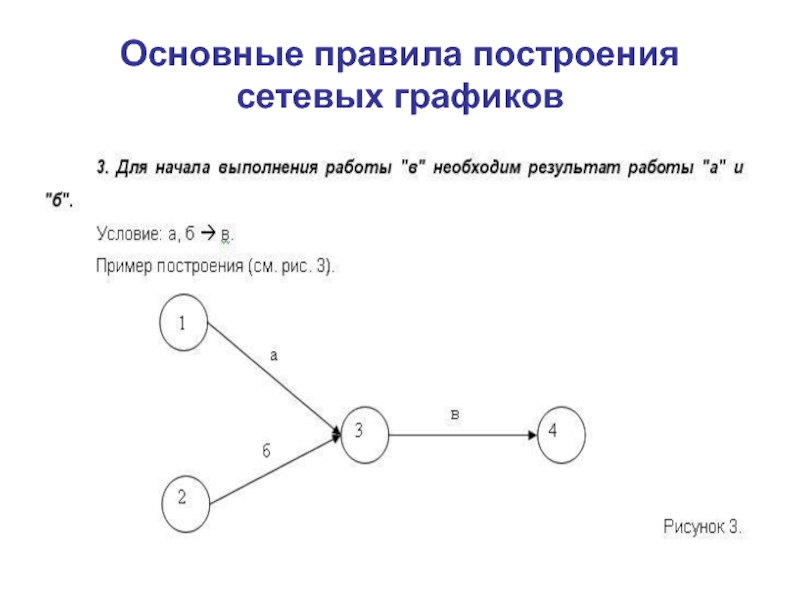
Слайд 9Основные правила построения сетевых графиков
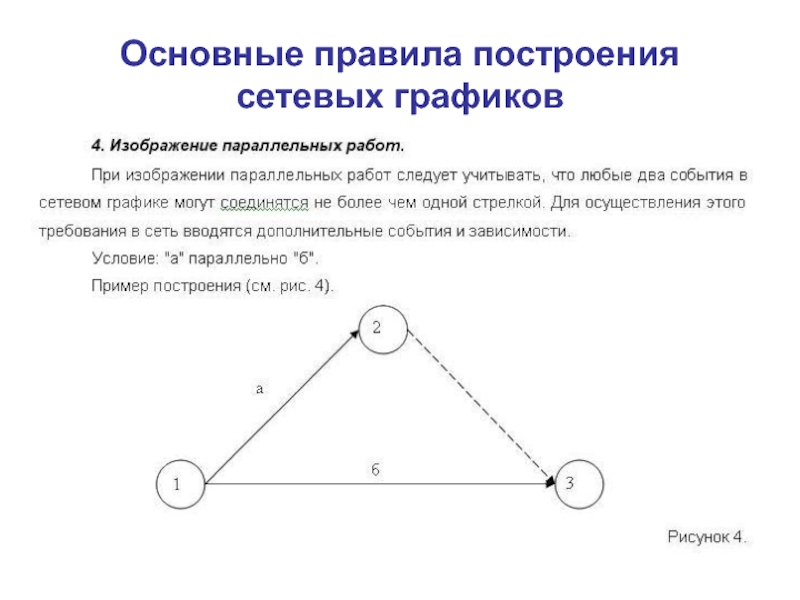
Слайд 10Основные правила построения сетевых графиков
В сетевом графике не должно быть
замкнутых контуров, ни один путь не должен дважды проходить через
одно и тоже событие.
В сетевом графике нельзя допускать тупиковых событий (кроме начального и конечного).
Слайд 11Нумерация событий методом вычеркивания дуг
Нумерация событий сетевого графика методом вычеркивания
дуг состоит в следующем:
1. Находится событие, которое не имеет ни
одной входящей дуги, ему присваивается ранг "0";
2. Затем на графике вычеркиваются все дуги, выходящие из события с рангом "0";
3. В результате одно или несколько событий могут оказаться без входящих дуг. Всем им присваивается ранг "1". Для любого из этих событий максимальное число дуг пути, соединяющего их с событием нулевого ранга, равно 1.
4. После вычеркивания всех дуг, выходящих из события первого ранга, получают вновь некоторое количество событий без входящих дуг. Их называют событиями второго ранга. (Далее аналогично).
5. После распределения всех событий по рангам нумерация осуществляется следующим образом: единственное событие нулевого ранга получает номер "0", события первого ранга в произвольном порядке получают номера 1,2,3 ... n1, где n1 – число событий первого ранга.
События второго ранга получают номера – n1+1, n1+2, ... n1+n2, где n2 – число событий второго ранга. (Далее аналогично).
Слайд 12Определение продолжительности работ
В связи с тем, что при построении
сетевого графика наряду с детерминированными работами (т.е. теми, для которых
можно точно определить длительность) имеется некоторое количество работ, которые никогда не выполнялись и точно определить продолжительность их выполнения не всегда представляется возможным.
При использовании PERT-сетей эта трудность преодолевается введением трех оценок продолжительности выполнения работ:
минимальная (оптимистическая) продолжительность (tmin) – это продолжительность работы при самых благоприятных условиях их выполнения;
максимальная (пессимистическая) продолжительность (tmax) – это продолжительность работ при самых неблагоприятных условиях ее выполнения;
наиболее вероятная продолжительность (tнв) – это продолжительность выполнения работы при наиболее часто встречающихся условиях ее выполнения.
Слайд 13Ожидаемая продолжительность работы (tож)
При использовании трех оценок ожидаемая
продолжительность и дисперсия определяются по следующим формулам:
Слайд 14Ожидаемая продолжительность работы (tож)
При использовании двух оценок ожидаемая продолжительность и
дисперсия определяются по следующим формулам:
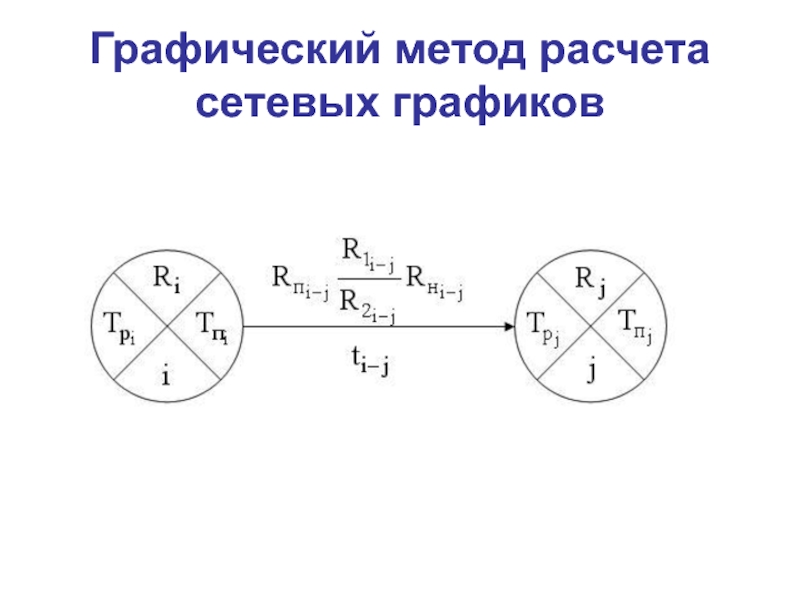
Слайд 15Графический метод расчета сетевых графиков
Слайд 16Графический метод расчета сетевых графиков
1. Определяем ранние и поздние сроки
свершения событий, резерв времени события.
Tpi - ранний срок свершения i-го
события.
Это самый ранний из возможных сроков свершения событий равен продолжительности максимального из предшествующих этому событию путей.
Tp1 = 0
Tpj = (Rpi + ti-j) max
Расчет проводится от начального события к конечному.
Слайд 17Графический метод расчета сетевых графиков
Tпi - поздний срок свершения i-го
события.
Это самый поздний из допустимых сроков свершения события равен разности
между длиной критического пути и продолжительностью следующего за этим событием пути.
Tпc = Tpc
Tпi = (Tпj - ti-j) min
Расчет проводится от конечного события к начальному.
Слайд 18Графический метод расчета сетевых графиков
Резерв времени события (Ri) определяется как
разность между поздними ранними сроками свершения данного события:
Ri = Tпi
– Tpi
Слайд 19Графический метод расчета сетевых графиков
Полный резерв времени работы определяется по
следующей формуле:
Rп(i-j) = Tпj - Tpi -ti-j,
где Rп(i-j) - полный резерв времени работы i-j.
где - полный резерв времени работы i-j
Полный резерв времени работы - это предельное время, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительности критического пути. Он определяется разницей между продолжительностью критического пути и продолжительностью максимального из путей, проходящих через данную работу.
Слайд 20Графический метод расчета сетевых графиков
Частный резерв первого вида определяется по
следующей формуле:
R1(i-j) = Tпj - Tпi - ti-j,
где R1(i-j) -
частный резерв первого вида работы (i-j).
Частный резерв первого вида возникает у работ (двух и более) с общим начальным событием за счет разности максимального пути, проходящего через данное событие и максимального пути, проходящего через данную работу. Он показывает на сколько (дней, недель, часов) можно увеличить работы, выходящие из данного события.
Слайд 21Графический метод расчета сетевых графиков
Частный резерв второго вида определяется по
следующей формуле:
R2(i-j) = Tpj - Tpi - ti-j,
где R2(i-j) - частный резерв второго вида работы (i-j).
Частный резерв второго вида образуется во всех случаях, когда в одно событие входят две или более работы с различной продолжительностью максимальных путей, проходящих через эти работы. Он образуется у работ, выполнение которых может быть закончено в более близкий срок по сравнению с ранним сроком наступления их общего конечного события.
Слайд 22Графический метод расчета сетевых графиков
Независимый (или свободный) резерв времени работы
определяется по следующей формуле:
Rн(i-j) = Tpj - Tпi -ti-j,
где Rн(i-j) - независимый резерв времени работы i-j;
Независимый (или свободный) резерв времени работы принадлежит только данной работе. Он образуется только в тех случаях, когда сама работа не принадлежит максимальным путям, проходящим через ее начальное и конечное событие и при условии, что Tpj - Tпi > t(i-j).
В общем виде независимый резерв может быть положительным, равным нулю и отрицательным. Отрицательный независимый резерв показывает время, которого не хватает у данной работы для выполнения ее к самому раннему сроку свершения ее конечного события при условии, что она была начата в самый поздний срок. В этом случае необходимо уделить больше внимания выполнению этой работы.
Слайд 23Критический путь
Условием, что данная работа принадлежит критическому пути, является равенство
всех ее резервов нулю. При этом необходимо учитывать, что равенство
нулю резерва времени события является необходимым условием критического пути, а равенство нулю полного резерва времени работы является достаточным условием критического пути.
Слайд 24Условия проверки
Для проверки правильности проведенных расчетов можно использовать следующие соотношения:
Rн(i-j)
= R1(i-j) + R2(i-j) -Rп(i-j)
Rн(i-j) = R1(i-j) – Rj
Rн(i-j) =
R2(i-j) –Ri
Rн(i-j) + Rп(i-j)= R1(i-j) + R2(i-j)
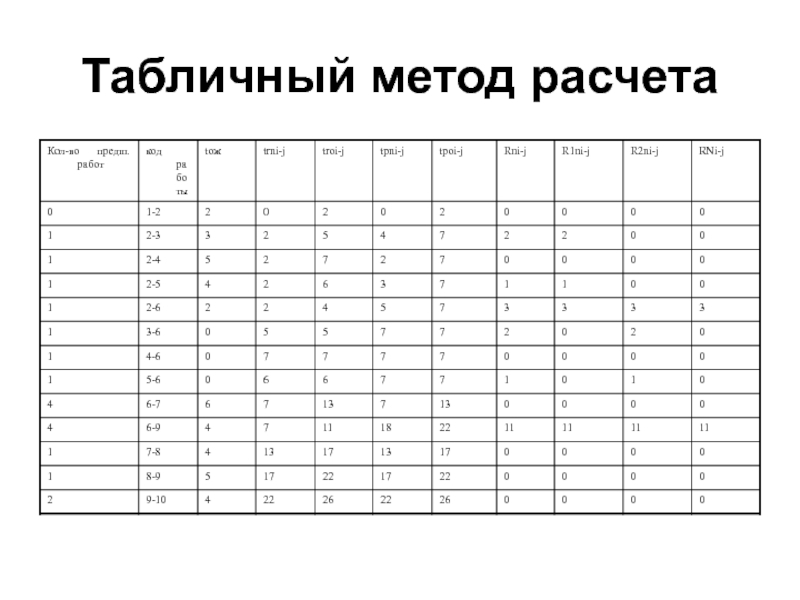
Слайд 25Табличный метод расчета
Пусть i - предшествующее событие, j -
последующее событие для работы i-j, 1 - начальное событие, с
- конечное событие.
Расчет проводится в следующей последовательности.
Определение раннего начала (trni-j) и раннего окончания (troi-j) работы (i-j).
Расчет начинаем с начального события.
trn1-j=0;
trni-j=(troпредшествующих работ)max;
troi-j=trni-j+ti-j.
Слайд 26Табличный метод расчета
Определение позднего начала (tpni-j) и позднего окончания (tpoi-j)
работы (i-j).
Расчет начинаем с конечного события:
tpoi-c=(tro(i-c))max;
tpni-c=tpo(i-c)-t(i-c)
Для остальных работ:
Tpo(i-j)=(tpnпоследующих работ)min;
tpni-j=tpo(i-j)-t(i-j).
Слайд 27Табличный метод расчета
Определение полного резерва работы (i-j).
Rni-j=tpo(i-j)-tro(i-j)=tpn(i-j)-trn(i-j)
Полный резерв времени работы
(i-j) - это предельное время, на которое можно увеличить продолжительность
данной работы, не изменяя при этом продолжительности критического пути. Полный резерв времени работы (i-j) определяется разницей между продолжительностью критического пути и продолжительностью максимального из путей, проходящих через работу (i-j).
Слайд 28Табличный метод расчета
Определение частного резерва первого вида
R1n(i-j) работы (i-j).
Определяются
группы работ, которые имеют общее начальное событие (одинаковое i). Для
выделенной группы работ частный резерв первого вида определяется, используя столбец таблицы, соответствующий позднему началу, по следующей формуле:
R1ni-j=tpn(i-j)-tpn(min) - (для этой группы работ)
Для остальных работ он равен нулю .
Частный резерв времени первого вида возникает у работ (двух и более) с общим начальным событием (i) за счет разности максимального пути, проходящего через событие (i) и максимального пути, проходящего через работу (i-j). Этот резерв показывает на сколько можно увеличить работы, выходящие из события (i) .
Слайд 29Табличный метод расчета
Определение частного резерва времени второго вида R2n(i-j) работы
(i-j).
Выделяются группы работ, которые имеют общее конечное событие (одинаковое j).
Для выделенной группы работ частный резерв второго вида определяется, используя столбец таблицы, соответствующий раннему окончанию, по формуле:
R2ni-j = (tro)max - troi-j - (для этой группы работ i-j).
Для остальных работ он равен нулю.
Частный резерв второго вида образуется в тех случаях, когда в одно событие входят две и более работы с различной продолжительностью максимальных путей.
Он образуется у работ, выполнение которых может быть закончено в более близкий срок по сравнению с ранним сроком наступления их общего конечного события (j).
Слайд 30Табличный метод расчета
Определение независимого или свободного резерва времени работы (i-j):
RNi-j=R1ni-j+R2ni-j-Rni-j
Независимый
(или свободный) резерв времени работы принадлежит только данной работе, образуется
только в тех случаях, когда сама работа не принадлежит максимальным путям, проходящим через ее начальное и конечное событие. Отрицательное значение независимого резерва времени показывает время, которого не хватит у данной работы для ее выполнения к самому раннему сроку свершения ее конечного события при условии, что она была начата в самый поздний срок. Выполнение работ с отрицательным значением независимого резерва времени нужно контролировать более тщательно.
Слайд 31Табличный метод расчета
Достаточным условием критического пути
является
равенство нулю полного
резерва работы:
Rn(i-j)=0
Слайд 32Определение вероятности выполнения проекта в срок
Вероятность свершения завершающего события
сетевого графика (Рк) в установленный (директивный) срок определяется по формуле:
где
z - аргумент нормальной функции распределения вероятностей;
Тдир - заданный (директивный) срок завершения комплекса работ;
Ткрит - ожидаемый (вычисленный) ранний срок свершения завершающего события комплекса работ;
sкрит - среднеквадратичное отклонение общей ожидаемой продолжительности
Слайд 33Определение вероятности выполнения проекта в срок (Рк)
Определение вероятности выполнения проекта
в срок (Рк) производится следующим образом:
1. вычисляется аргумент нормальной
функции распределения вероятностей (z);
2. по таблице значений нормальной функции распределения вероятностей находится Ф(z).
Из опыта сетевого планирования и управления рекомендуется интервал значений вероятностей 0,35 < Рк <0,65 (или по другим источникам 0,25 < Рк < 0,5).
При этом, если:
Рк < 0,35, то вероятность срыва запланированного срока выполнения комплекса работ велика, поэтому необходима оптимизация сетевого графика. Если оптимизация не дает желаемого результата, то необходимо ставить вопрос о переносе директивного срока или о дополнительном выделении ресурсов;
Рк > 0,65, то комплекс работ будет выполнен в запланированный срок, но при этом в план заложено избыточное количество ресурсов;
0,35 < Рк < 0,65, то сетевой график может быть принят без изменений.
Слайд 34Построение масштабного сетевого графика комплекса работ
Построение масштабного сетевого графика
производится в следующей последовательности:
На координатной плоскости, где по оси абсцисс
отложены сроки выполнения работ в рабочих днях, ориентируясь на топологию безмасштабного сетевого графика, располагают события по ранним срокам их свершения.
Под осью абсцисс располагается вторая шкала в календарных днях.
События в соответствии с работами безмасштабного сетевого графика соединяются тонкими линиями.
На этих тонких линиях откладываются в масштабе продолжительности соответствующие работы, которые затем прорисовываются более толстыми линиями и заканчиваются стрелками.
Критический путь выделяется двойной стрелкой или цветом.
Слайд 35Основы оптимизации сетевого графика
Оптимизация сетевого графика представляет собой процесс
улучшения организации выполнения комплекса работ с учетом установленного срока и
использования ресурсов.
Оптимизация сетевого графика осуществляется в основном за счет:
перераспределения временных, материальных, энергетических и трудовых ресурсов;
интенсификации выполнения работ критического пути в результате привлечения дополнительного количества работников и оборудования, а также материального стимулирования работников.
В зависимости от полноты решаемых задач оптимизация может быть разделена на частную и комплексную.
К частной оптимизации относится:
минимизация времени выполнения проекта при заданной стоимости;
минимизация потребляемых ресурсов (в качестве ресурсов выступают: трудовые ресурсы, оборудование, материалы, энергетические ресурсы и т.д.);
минимизация стоимости при заданном времени выполнения.
Под комплексной оптимизацией понимается нахождение оптимального соотношения величин затрат и сроков выполнения работы в зависимости от конкретных целей.
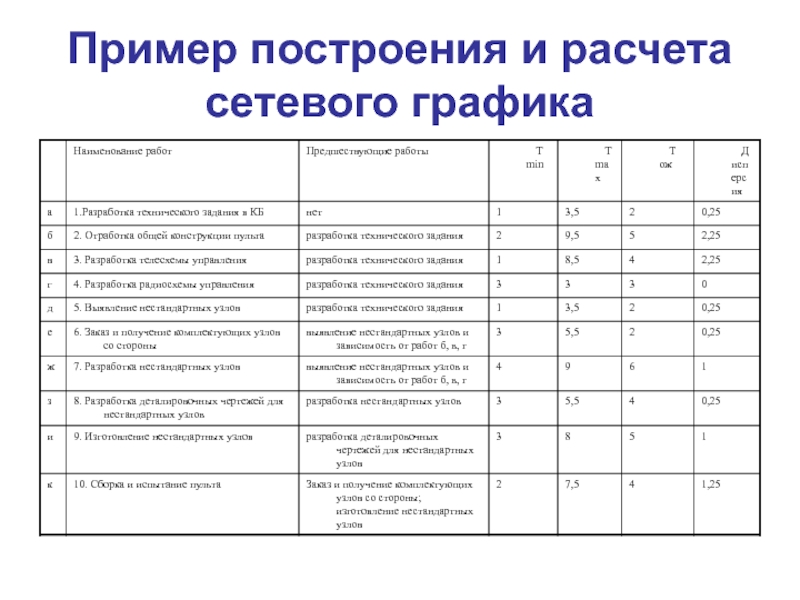
Слайд 36Пример построения и расчета сетевого графика
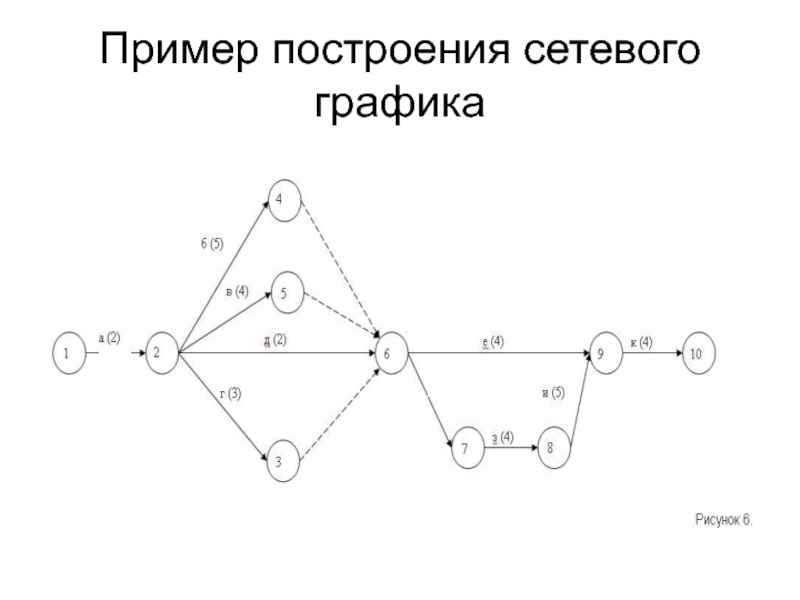
Слайд 38Пример построения сетевого графика