Слайд 1Дополнительные главы математики
Лекция № 1 на тему:
«Основные статистические
методы анализа экспериментальных данных. Применение информационных технологий для обработки результатов
эксперимента»
Лектор: кандидат технических наук
доцент кафедры высшей математики
Гордеева Елена Львовна
2020 г.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Российский химико-технологический университет имени Д. И. Менделеева
______________________________________
Слайд 2Предмет, цель и задачи дисциплины «Дополнительные главы математики»
Предмет: изучение и
практическая реализация основных методов статистической обработки экспериментальных данных.
Цель дисциплины: знакомство
с современными методами статистической обработки экспериментальных данных с использованием средств информационных технологий на основе углублённого изучения курса математической статистики.
Основные задачи дисциплины : получение представлений об актуальных проблемах использования статистических методов в химии, химической технологии, биотехнологии и экологии, а также практическая реализация основных подходов к анализу данных с использованием вероятностно-статистических и логико-алгебраических методов.
Результат: освоение приёмов и методов обработки статистической информации, регрессионного и корреляционного анализа, дисперсионного анализа, знание основных методов анализа многомерных данных, а также овладение практическими навыками обработки экспериментальных данных с использованием информационных технологий.
Слайд 3Разделы лекции
Основные направления статистической обработки данных
Информационные технологии для статситческой обработки
данных
Моделирование законов распределения случайных величин
Предварительная обработка экспериментальных данных
Слайд 41.Основные направления статистической обработки данных
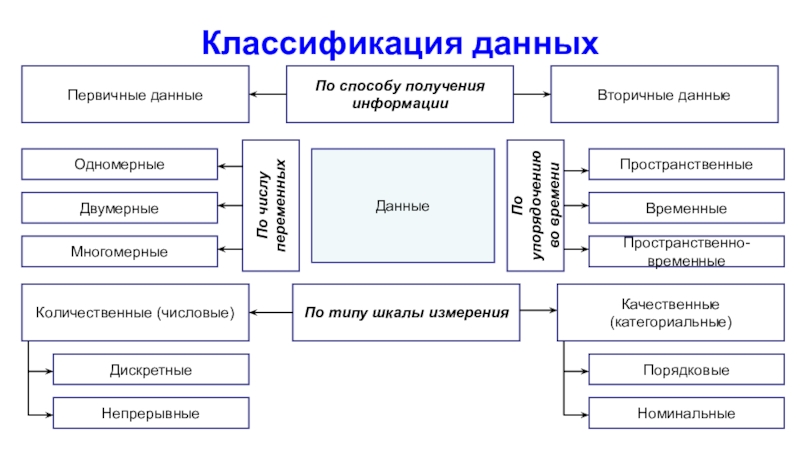
Слайд 5Статистические данные и их анализ
Данные – совокупность сведений, зафиксированных на
определённом носителе в форме, пригодной для их постоянного хранения, передачи
и обработки.
Цель анализа данных:
анализ и отображение конкретной собранной информации – статистическое описание, описательная (дескриптивная) статистика
описание всего класса явлений по имеющимся выборочным данным, характеризующим только часть этого класса – аналитическая статистика.
Наука о данных (англ. Data Science) – раздел информатики, изучающий проблемы анализа, обработки и представления данных в цифровой форме.
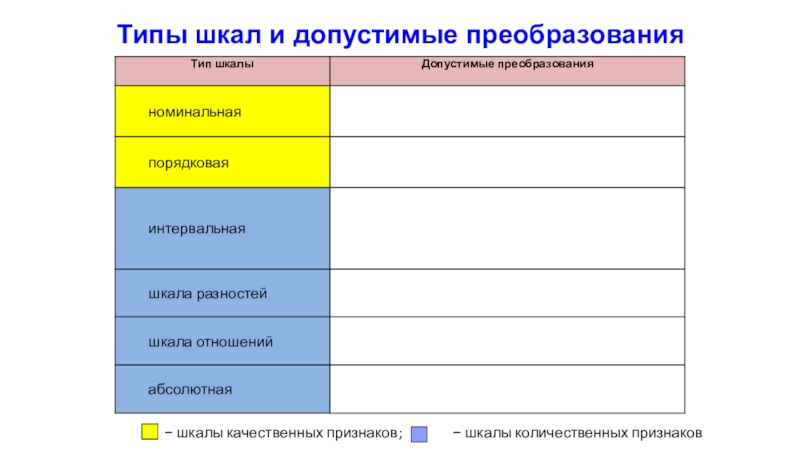
Слайд 7Типы шкал и допустимые преобразования
− шкалы качественных признаков;
− шкалы количественных признаков
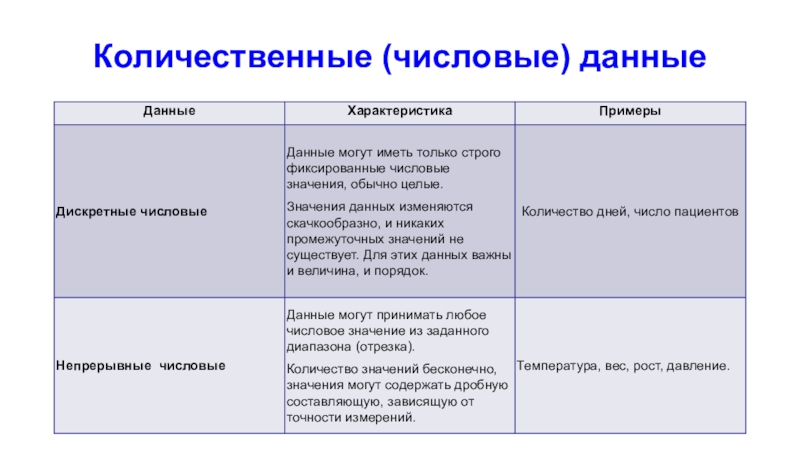
Слайд 9Количественные (числовые) данные
Слайд 102. Информационные технологии для статистической обработки данных
Статистические пакеты:
универсальные (R, SPSS,STADIA,
Statistica);
специальные («Эвриста», «Мезозавр»);
профессиональные (SAS, BMDP, IMSL);
Статистические функции, включенные
в математические пакеты общего назначения Mathcad, Mathlab, Maple, Mathematica;
Табличные процессоры − пакеты прикладных программ для автоматизации расчётов (MS Excel, OpenOffice).
Слайд 11Возможности MS Excel для статистической обработки данных
Вычисления в таблицах и
визуализация данных и расчётов
Статистические и математические функции (СРЗНАЧ, ДИСП, ЛИНЕЙН,
ЧАСТОТА, МАКС, МИН, МОПРЕД и др.) в категориях Статистические и Математические
Инструменты Пакета анализа (Данные→Анализ →Анализ данных)
Программирование в VBA (Visual Basic for Applications)
Слайд 123.Моделирование законов распределения случайных величин
Соотношение, устанавливающее связь между возможными значениями
случайной величины и их вероятностями, называется законом распределения случайной величины.
Универсальным
способом задания закона распределения вероятностей является функция распределения F(x).
Функцией распределения случайной величины Х называется функция F(x), которая для любого числа x R равна вероятности события (X < x):
F(x) = P(X < x).
Плотностью распределения вероятностей непрерывной случайной величины Х называется производная её функции распределения:
f(x) = F’(x).
Слайд 13Моделирование нормального закона распределения
Слайд 14Функции нормального распределения в MS Excel
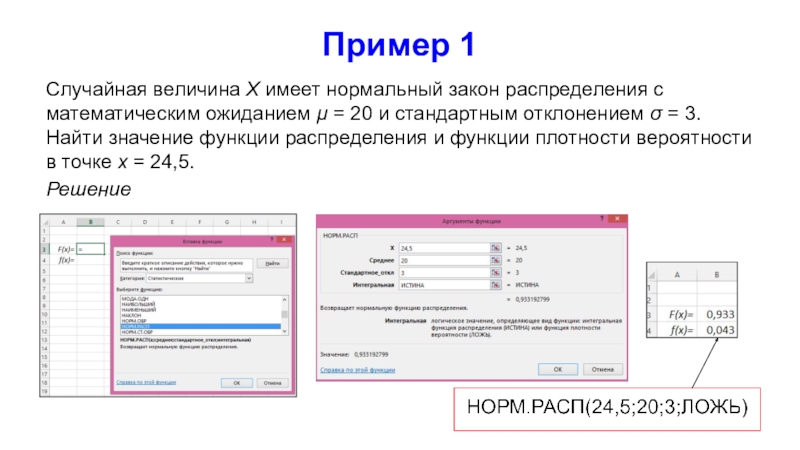
Слайд 15Пример 1
Случайная величина Х имеет нормальный закон распределения с математическим
ожиданием μ = 20 и стандартным отклонением = 3.
Найти значение функции распределения и функции плотности вероятности в точке х = 24,5.
Решение
Слайд 162) НОРМ.СТ.РАСП(z; интегральная) определяет значение функции распределения или функции плотности
вероятности стандартного нормального распределения, z − значение аргумента, для которого
вычисляется функция. Эта функция используется вместо таблицы для стандартного распределения вероятностей.
Пример 2. Случайная величина Х имеет нормальный закон распределения с математическим ожиданием μ = 3 и стандартным отклонением = 2. Найти вероятность попадания случайной величины в интервал (1; 2,5).
Решение
1 способ. Ввести формулу:
=НОРМ.РАСП(2,5;3;2;ИСТИНА)-НОРМ.РАСП(1;3;2;ИСТИНА)
Результат: 0,242638.
2 способ. Ввести формулу:
=НОРМ.СТ.РАСП((2,5-3)/2;ИСТИНА)-НОРМ.СТ.РАСП((1-3)/2;ИСТИНА)
Результат: 0,242638.
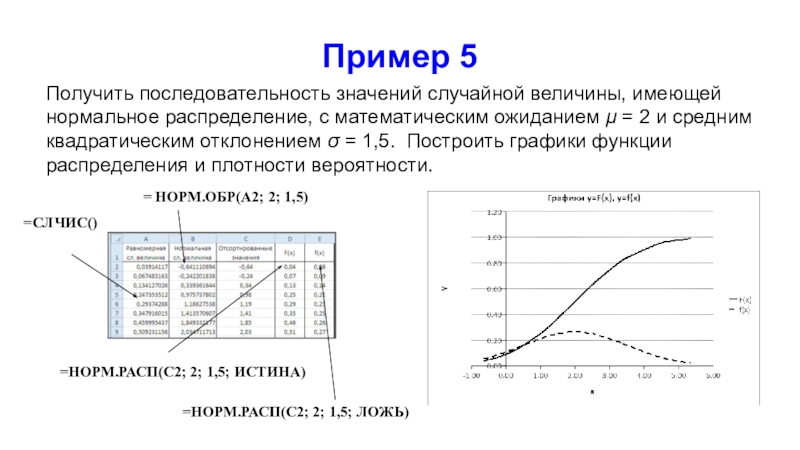
Слайд 18Пример 5
Получить последовательность значений случайной величины, имеющей нормальное распределение, с
математическим ожиданием μ = 2 и средним квадратическим отклонением σ
= 1,5. Построить графики функции распределения и плотности вероятности.
=СЛЧИС()
= НОРМ.ОБР(A2; 2; 1,5)
=НОРМ.РАСП(С2; 2; 1,5; ИСТИНА)
=НОРМ.РАСП(С2; 2; 1,5; ЛОЖЬ)
Слайд 19Биномиальный закон распределения
Слайд 20Моделирование биномиального распределения
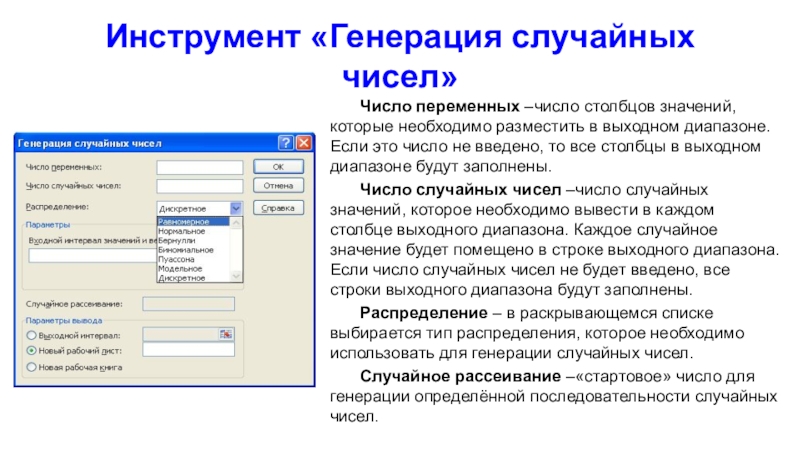
Слайд 22Инструмент «Генерация случайных чисел»
Число переменных –число столбцов значений, которые необходимо
разместить в выходном диапазоне. Если это число не введено, то
все столбцы в выходном диапазоне будут заполнены.
Число случайных чисел –число случайных значений, которое необходимо вывести в каждом столбце выходного диапазона. Каждое случайное значение будет помещено в строке выходного диапазона. Если число случайных чисел не будет введено, все строки выходного диапазона будут заполнены.
Распределение – в раскрывающемся списке выбирается тип распределения, которое необходимо использовать для генерации случайных чисел.
Случайное рассеивание –«стартовое» число для генерации определённой последовательности случайных чисел.
Слайд 23Генеральная совокупность и выборка
Генеральная совокупность - множество возможных значений случайной
величины Х. Под законом распределения (распределением) генеральной совокупности Х понимают
закон распределения вероятностей случайной величины Х.
В результате эксперимента получают реализацию случайной выборки – совокупность значений
x1, x2, …, xn
которые называются выборкой из генеральной совокупности Х. Число n характеризует объём выборки, а числа xi представляют собой элементы выборки.
Для получения выборки в Пакете анализа используется инструмент «Выборка».
Слайд 24Методы анализа данных
Предварительный анализ данных. Описательная статистика
Статистическое оценивание параметров генеральной
совокупности
Проверка статистических гипотез
Дисперсионный анализ
Корреляционный анализ
Регрессионный анализ
Классификация многомерных наблюдений
Анализ временных рядов
Слайд 254.Предварительная обработка результатов эксперимента
Цель: представить наблюдаемые данные в возможно более
компактной и простой форме, позволяющий выявить в них закономерности и
связи.
Этапы предварительной обработки:
представление данных в виде таблиц и графиков;
получение статистических оценок.
Слайд 26Графическое представление данных
Применяется для:
Распознавания структуры и характерных особенностей данных;
Обнаружения ошибок
в данных;
Исследования взаимосвязи между случайными величинами;
Оценки соответствия данных выбранным
моделям;
Обнаружения новых явлений;
Выявления необходимости в корректировке данных, а также определения способа ее осуществления (преобразование данных, сбор дополнительных данных или изменение условий эксперимента).
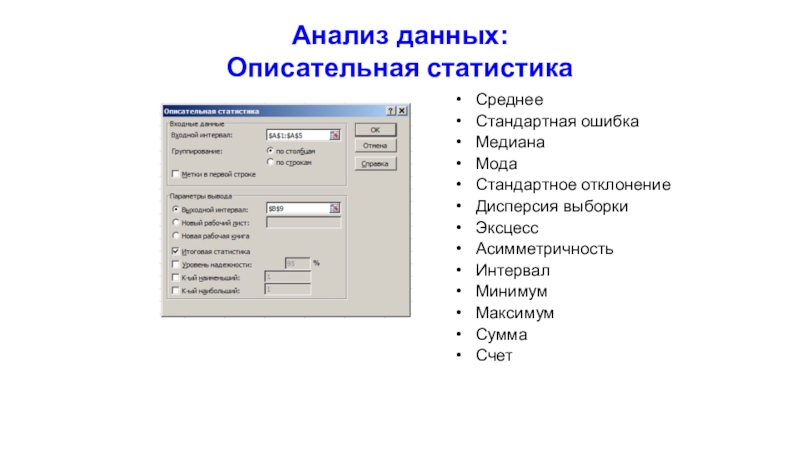
Слайд 27Анализ данных:
Описательная статистика
Среднее
Стандартная ошибка
Медиана
Мода
Стандартное отклонение
Дисперсия выборки
Эксцесс
Асимметричность
Интервал
Минимум
Максимум
Сумма
Счет
Слайд 28Для представление качественных данных используют:
Таблицы
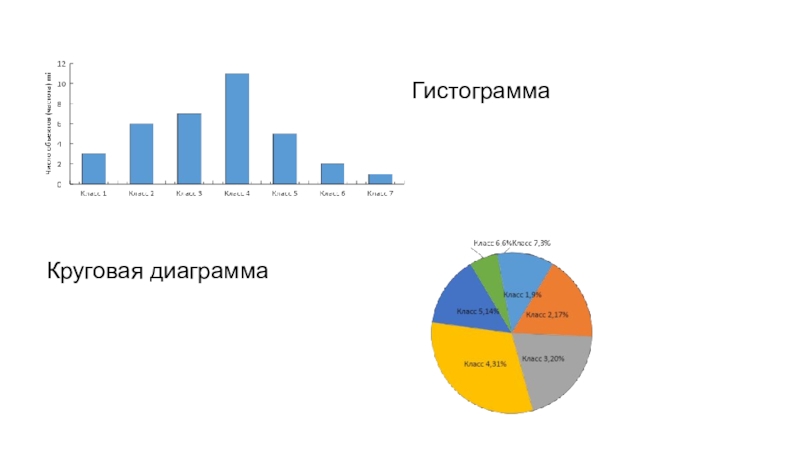
Столбиковые диаграммы (гистограммы)
Круговые диаграммы
Точечные графики и
т.д.
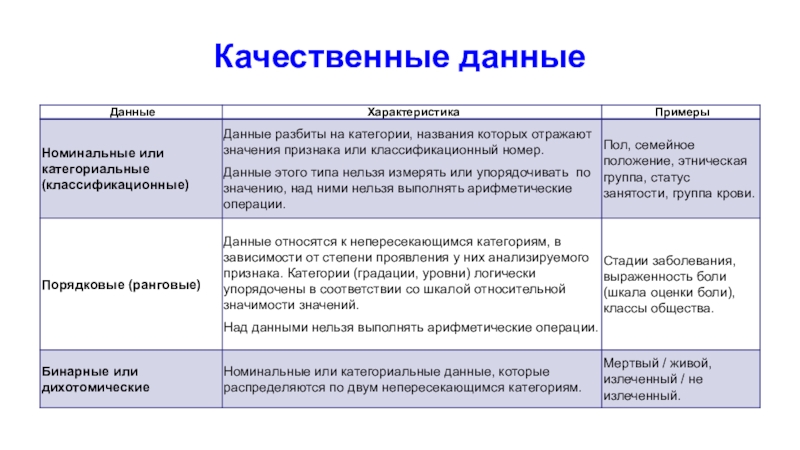
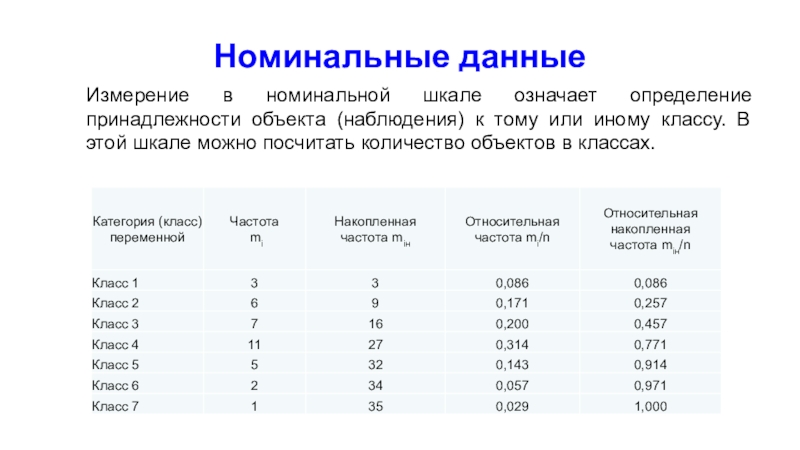
Слайд 29Номинальные данные
Измерение в номинальной шкале означает определение принадлежности объекта (наблюдения)
к тому или иному классу. В этой шкале можно посчитать
количество объектов в классах.
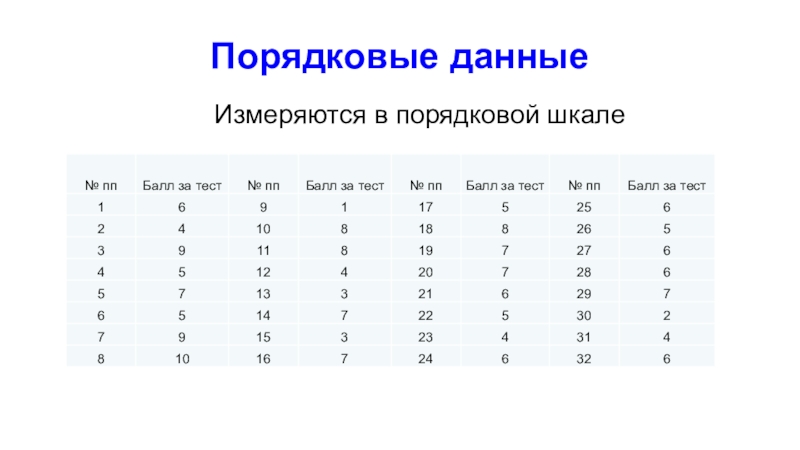
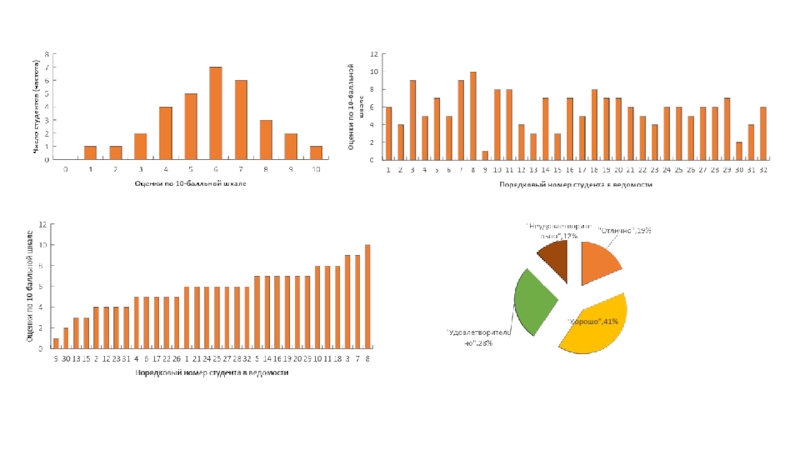
Слайд 31Порядковые данные
Измеряются в порядковой шкале
Слайд 33Для представления количественных данных используют
Вариационный дискретный и интервальный вариациаонный ряд
Полигон
Гистограмма
Кумулята
и и т.д.
Слайд 35Группировка дискретных количественных данных
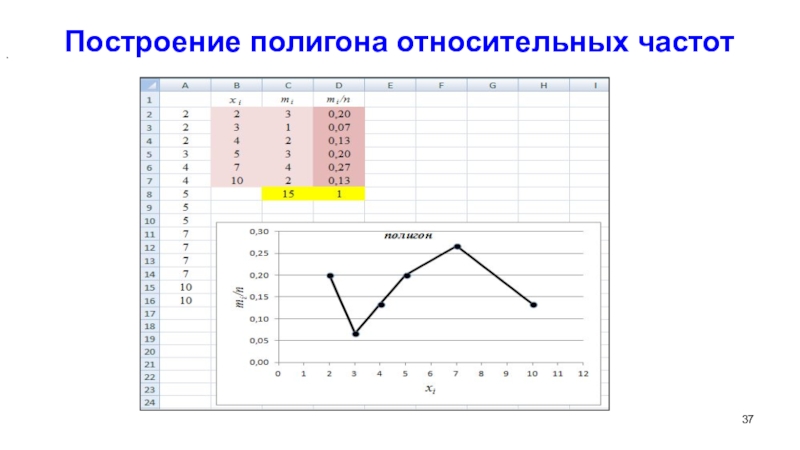
Слайд 37Построение полигона относительных частот
.
,
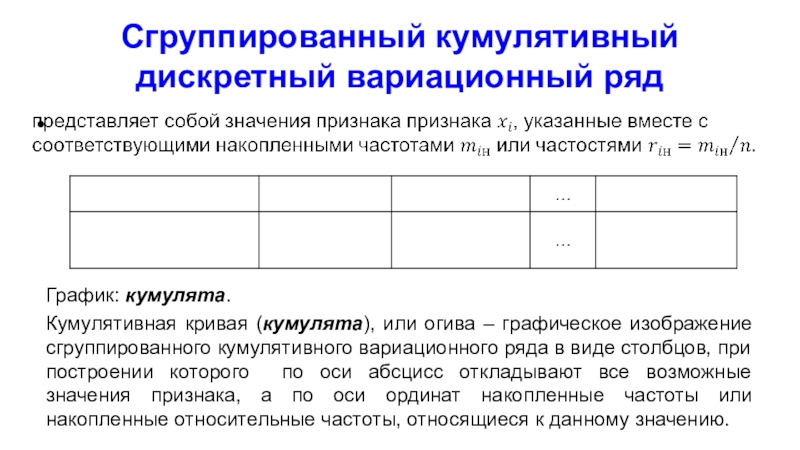
Слайд 38Сгруппированный кумулятивный дискретный вариационный ряд
График: кумулята.
Кумулятивная кривая (кумулята), или огива
– графическое изображение сгруппированного кумулятивного вариационного ряда в виде столбцов,
при построении которого по оси абсцисс откладывают все возможные значения признака, а по оси ординат накопленные частоты или накопленные относительные частоты, относящиеся к данному значению.
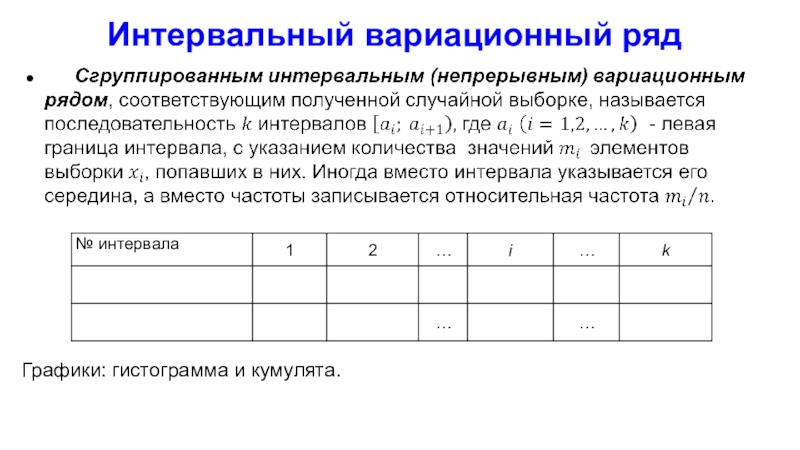
Слайд 39Интервальный вариационный ряд
Графики: гистограмма и кумулята.
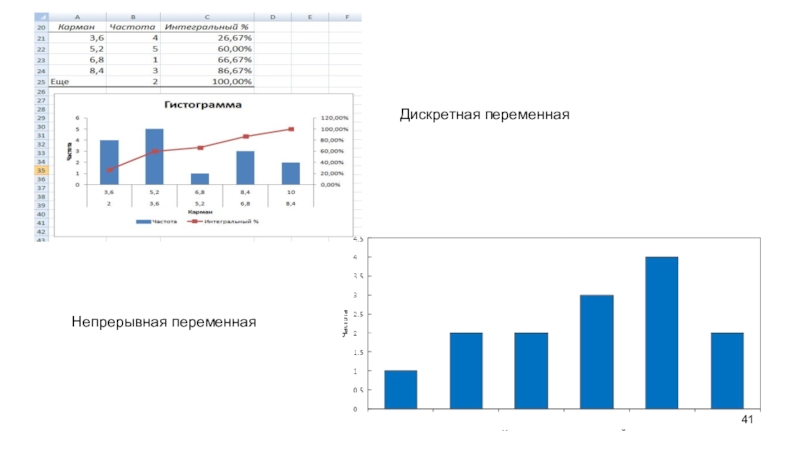
Слайд 40Столбцы на гистограмме и кумуляте должны соприкасаться, не иметь участков,
куда не попадают значения признака.
Для построения гистограммы и кумуляты в
MS Excel можно использовать инструмент Пакета анализа «Гистограмма».
Слайд 41Непрерывная переменная
Дискретная переменная
Слайд 42Алгоритм построения гистограммы интервального ряда
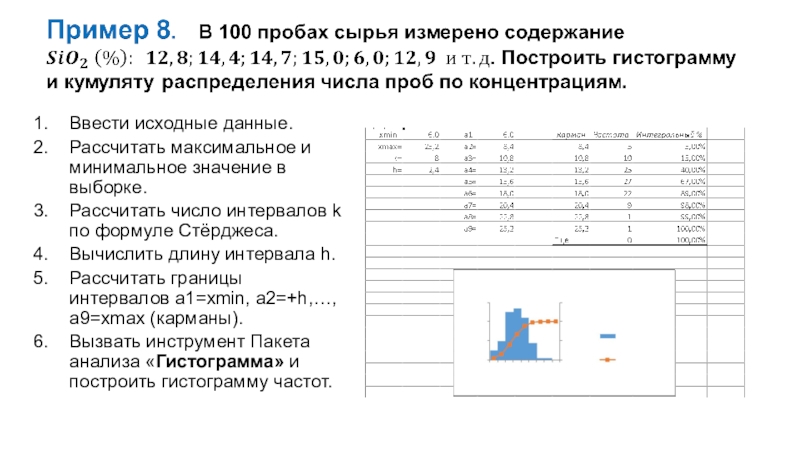
Слайд 43Ввести исходные данные.
Рассчитать максимальное и минимальное значение в выборке.
Рассчитать число
интервалов k по формуле Стёрджеса.
Вычислить длину интервала h.
Рассчитать границы интервалов
a1=xmin, a2=+h,…, a9=xmax (карманы).
Вызвать инструмент Пакета анализа «Гистограмма» и построить гистограмму частот.
Слайд 44Заключение
Рассмотрены основные направления статистической обработки данных и средства информационных технологий
для практической реализации этой задачи.
Приведены примеры моделирования распределений случайных
величин с использованием статистических функций табличного процессора MS Excel и инструментов надстройки Анализ данных.
Рассмотрены основные способы представления качественных данных: таблицы, гистограммы, круговые диаграммы.
Рассмотрены основные способы представления количественных данных (дискретных и непрерывных) в виде дискретного вариационого ряда, интервального вариационного ряда, а также построение графиков: полигона, гистограммы и кумуляты.
Слайд 45Литература
Анализ данных: учебник для академического бакалавриата / под. ред. В.С.Мхитаряна.
– М. : Издательство Юрайт, 2016 г. – 490 с.
Вадзинский
Р. Статистические вычисления в среде Excel. Библиотека пользователя. – СПб. : Питер, 2008. – 608 с.