Слайд 1Дополнительные главы математики
Лекция № 3 на тему:
«Проверка статистических
гипотез»
Лектор: кандидат технических наук
доцент кафедры высшей математики
Гордеева Елена Львовна
2020 г.
Министерство
науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Российский химико-технологический университет имени Д. И. Менделеева
______________________________________
Слайд 2Разделы лекции
Статистические гипотезы и их виды
Основной принципы проверки гипотез
3.
Сравнение двух дисперсий нормально распределённых генеральных совокупностей
4. Проверка гипотезы о
равенстве средних
5. Проверка гипотезы о виде закона распределения
6. Ранговые критерии
6.1. U - критерий Манна-Уитни
6.2. T - критерий Вилкоксона
Слайд 31. Статистические гипотезы и их виды
Под статистической гипотезой понимают всякое
высказывание о генеральной совокупности, проверяемое по выборке (по результатам наблюдений).
Статистическими
методами гипотезу можно только опровергнуть или не опровергнуть, но не доказать.
Гипотезы делятся на:
Параметрические;
Непараметрические.
Параметрическими называются гипотезы о параметрах распределения известного вида. Например: дисперсии двух нормальных совокупностей равны между собой.
Непараметрическими называются гипотезы о виде неизвестного распределения. Например: генеральная совокупность распределена по нормальному закону.
Слайд 4Нулевая и альтернативная гипотезы
Выдвинутая гипотеза называется нулевой (или основной) и
обозначается H0. Гипотеза, которая противоречит нулевой, называется конкурирующей гипотезой (или
альтернативной) и обозначается H1.
Это означает, что являются противоположными следующие два события:
по выборке будет принято решение о справедливости для генеральной совокупности гипотезы H0;
по выборке будет принято решение о справедливости для генеральной совокупности гипотезы H1.
Сущность нулевой гипотезы: разница между генеральными параметрами сравниваемых групп равна нулю и различия, наблюдаемые между выборочными характеристиками носят исключительно случайный характер.
Пример:Из нормально распределённых совокупностей X и Y извлечены выборки с параметрами: M(X) и σx (из выборки X);M(Y) и σy (из выборки Y).
Нулевая гипотеза Н0: M(X)=M(Y) и σx= σy, т.е. M(X)-M(Y)=0 и σx- σy=0.
Альтернативная гипотеза Н1: M(X)-M(Y)≠0 и σx- σy≠0.
Слайд 62. Основные принципы проверки гипотез
Проверка гипотезы - сопоставление выдвинутой гипотезы
с выборочными данными.
Для проверки нулевой гипотезы используют специально подобранную случайную
величину, распределение которой известно. Эту величину называют критерием. Наблюдаемым значением Zнабл называют значения критерия, вычисленное по выборкам. Множество всех возможных значений критерия разбивают на два непересекающихся подмножества: одно из них содержит значения, при которых нулевая гипотеза отвергается, а другая – при которых она принимается.
Критическая область - совокупность значений критерия, при которых нулевую гипотезу отвергают.
Область допустимых значений (область принятия гипотезы) - совокупность значений критерия, при которых гипотезу принимают.
Слайд 7Точки, отделяющие критическую область от области принятия гипотезы, называют критическими
точками или границами.
Если наблюдаемое значение критерия принадлежит критической области, то
основная гипотеза H0 отклоняется и принимается альтернативная гипотеза H1, если же наблюдаемое значение критерия Zнабл принадлежит области принятия гипотезы, то принимается H0, отвергается H1.
Возможные решения при проверке гипотез:
Слайд 8При проверке гипотез возможны ошибочные заключения двух типов:
Ошибка первого рода
– решение отвергнуть нулевую гипотезу H0 и принять конкурирующую гипотезу
H1 , если на самом деле H0 верна.
Ошибка второго рода – решение принять нулевую гипотезу H0 и отвергнуть конкурирующую гипотезу, если на самом деле гипотеза H1 верна.
Уровень значимости - это вероятность ошибки первого рода (вероятность попадания в критическую область).
Стандартные уровни статистической значимости:
0,05; 0,01; 0,001.
Вероятность ошибки второго рода обозначается β. 1- β называется мощностью критерия.
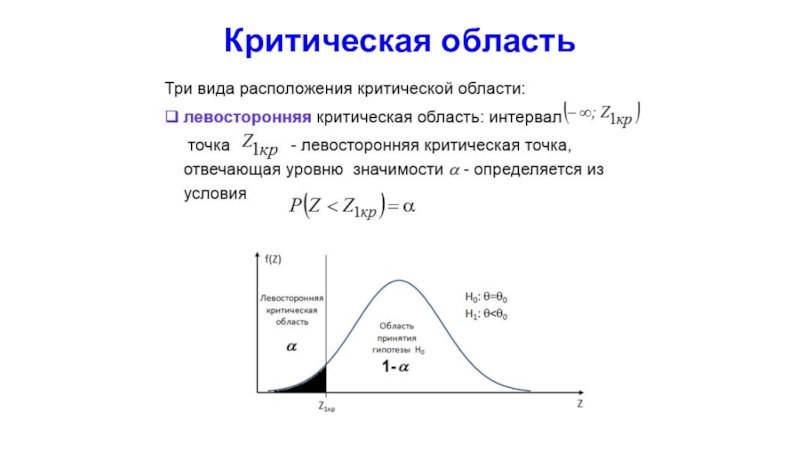
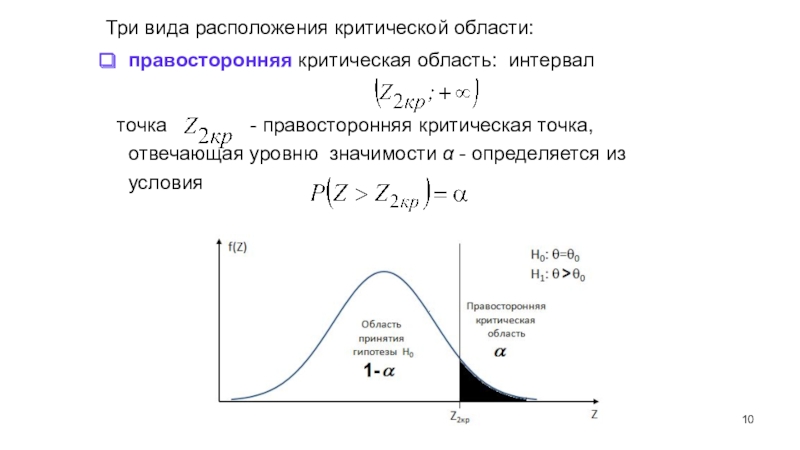
Слайд 10Три вида расположения критической области:
правосторонняя критическая область: интервал
точка -
правосторонняя критическая точка, отвечающая уровню значимости - определяется из условия
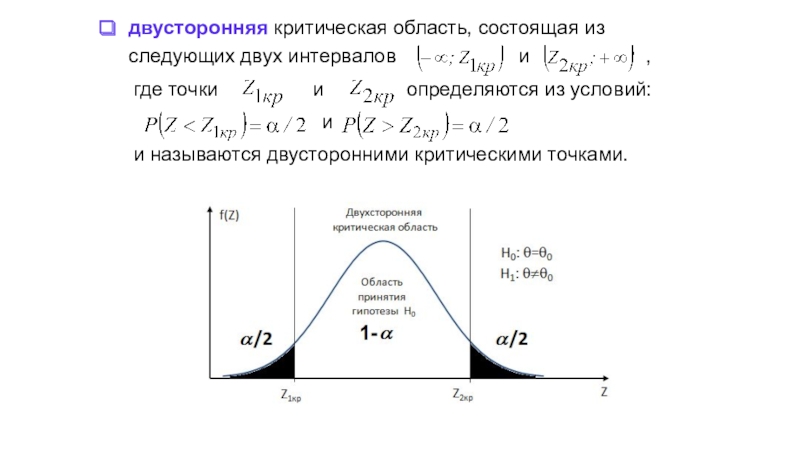
Слайд 11двусторонняя критическая область, состоящая из следующих двух интервалов
и
,
где точки и определяются из условий:
и
и называются двусторонними критическими точками.
Слайд 12Схема проверки гипотезы
Формирование нулевой гипотезы H0, основываясь на выборочных данных
и конкретных условиях задачи, и конкурирующей гипотезы H1.
Выбор вероятности ,
которую называют уровнем значимости нулевой гипотезы H0.
Подбор по выборочным данным случайной величины Z, распределение которой называется критерием для проверки нулевой гипотезы.
Определение границы Zкр критической области для проверки нулевой гипотезы с уровнем значимости .
Если вычисленное по выборке значение критерия Zнабл попадает в критическую область, то нулевая гипотеза отвергается и принимается конкурирующая гипотеза . Если же нет, то нет оснований отвергать нулевую гипотезу.
Слайд 13Виды статистических критериев
Статистические критерии делятся на параметрические и непараметрические.
Параметрические
критерии - статистические критерии, которые используют в процессе расчетов параметры
распределения: средние значения и дисперсии (среднеквадратические отклонения). Помимо этого, должно выполняться требование соответствия эмпирического распределения нормальному распределению.
Непараметрическими называются критерии, не включающие в формулу расчета параметры распределения, и не предполагающие знания функции распределения. Эти критерии оперируют частотами или рангами.
Критерии используют при сравнении выборок с номинальными и порядковыми признаками, а также для выборок, измеренных в количественных шкалах, для которых закон распределения неизвестен или отличается от нормального.
Слайд 143. Сравнение двух дисперсий нормальных генеральных совокупностей
Требуется сравнить D(X) и
D(Y) генеральных совокупностей.
Слайд 16Пример 1.
Для изучения воспроизводимости работы pH-метра в кислой и щелочной
среде проведены измерения pH в семи аликвотах буферного раствора I
и восьми аликвотах буферного раствора II. Можно ли считать воспроизводимость измерений неизменной в диапазоне pH от 4 до 9?
Так как Fнабл
Слайд 174. Проверка гипотезы о равенстве средних
Пусть в результате наблюдений
получены независимые выборки из нормально распределённых генеральных совокупностей X и
Y: (x1, x2, …, xn) объёма n и (y1, y2, …, ym) объёма m.
Требуется проверить гипотезу о том, что математические ожидания случайных величин X и Y равны, то есть нулевая гипотеза H0: M(X) = M(Y).
Пусть дисперсии случайных величин D(X) и D(Y) известны.
В качестве критерия используется статистика
Слайд 18Сравнение двух средних нормальных генеральных совокупностей
Слайд 19Пример 2. Проверка гипотезы о равенстве средних
Считая, что вес кроликов
подчиняется нормальному закону распределения, выяснить, показал ли эксперимент существенное различие
в средних привесах. Проверить гипотезу на уровне значимости =0,01.
Изучали влияние кобальта на массу тела кроликов. Опыт проводили на двух группах животных: опытной (О) и контрольной (К). Кролики из опытной группы ежедневно получали добавку к рациону в виде водного раствора по 0,06 г вещества на 1 кг живой массы тела. Результаты измерения веса в граммах приведены в таблице:
Контрольная группа
M(Y)
Опытная группа
M(X)
M(X)>M(Y)?
Слайд 20Проверка гипотезы о равенстве средних
Нулевая гипотеза H0: M(X)=M(Y)
Конкурирующая гипотеза H1:
M(X)>M(Y)
Уровень значимости =0,01
1. Оценки математических ожиданий:
2. Исправленные выборочные дисперсии:
Слайд 21Проверка гипотезы о равенстве средних
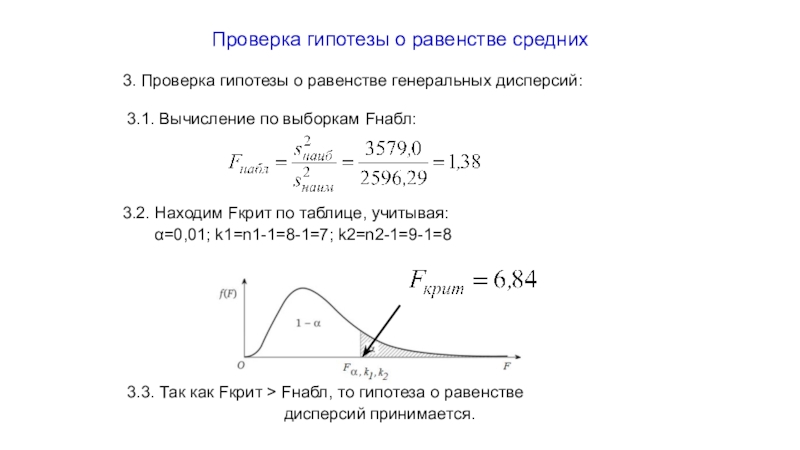
3. Проверка гипотезы о равенстве генеральных
дисперсий:
3.1. Вычисление по выборкам Fнабл:
3.2. Находим
Fкрит по таблице, учитывая:
=0,01; k1=n1-1=8-1=7; k2=n2-1=9-1=8
3.3. Так как Fкрит > Fнабл, то гипотеза о равенстве
дисперсий принимается.
Слайд 22Проверка гипотезы о равенстве средних
4. Проверка гипотезы о равенстве средних:
4.1. Вычисление по выборкам Tнабл:
4.2. Находим Tкрит
по таблице, учитывая:
=0,01; k=n1+n2-2=15
4.3. Так как Tнабл > Tкрит, то гипотеза о равенстве
средних отвергается, т.е. M(X)>M(Y).
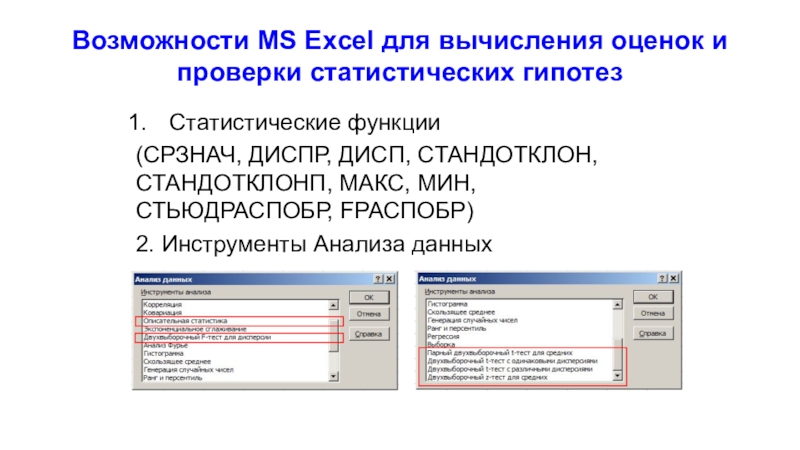
Слайд 23Возможности MS Excel для вычисления оценок и проверки статистических гипотез
Статистические функции
(СРЗНАЧ, ДИСПР, ДИСП, СТАНДОТКЛОН, СТАНДОТКЛОНП, МАКС, МИН, СТЬЮДРАСПОБР, FРАСПОБР)
2.
Инструменты Анализа данных
Слайд 245. Проверка гипотезы о законе распределения
Знание закона распределения позволяет правильно
выбрать методы статистической обработки результатов эксперимента, а также определить вид
модели, описывающей зависимость между анализируемыми признаками.
Для нахождения закона распределения генеральной совокупности при отсутствии предварительных данных по выборке строят статистический ряд, гистограмму или полигон частот. Сравнивая полученный график с графиками плотности вероятностей известных законов распределения, выдвигают гипотезу H0 о виде закона распределения.
Далее проверяют гипотезу H0 с помощью критериев согласия.
Слайд 25Проверка гипотез о законе распределения генеральной совокупности
Слайд 27Схема проверки гипотезы о законе распределения по критерию Пирсона
Слайд 28Схема проверки гипотезы о законе распределения по критерию Пирсона
5. Находится
выборочное значение критерия К.Пирсона по формуле:
Слайд 30Проверка гипотезы о нормальном законе распределения
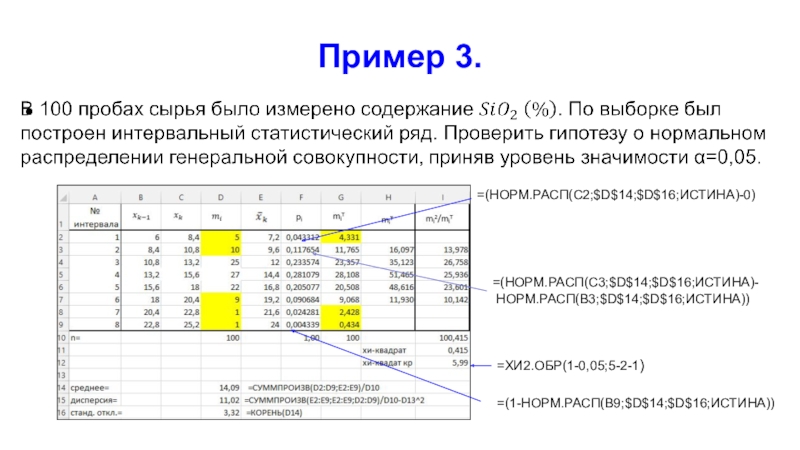
Слайд 31Пример 3.
=ХИ2.ОБР(1-0,05;5-2-1)
=(НОРМ.РАСП(C3;$D$14;$D$16;ИСТИНА)-
НОРМ.РАСП(B3;$D$14;$D$16;ИСТИНА))
=(НОРМ.РАСП(C2;$D$14;$D$16;ИСТИНА)-0)
=(1-НОРМ.РАСП(B9;$D$14;$D$16;ИСТИНА))
Слайд 326. Ранговые критерии
6.1. U - критерий Манна-Уитни
Критерий предназначен для проверки
гипотезы о статистической однородности двух независимых выборок, т.е. для оценки
различий между двумя выборками по уровню какого-либо признака, количественно измеренного.
Он позволяет выявлять различия между малыми выборками, когда n1, n2 3 или n1 = 2, n2 5 (n1 и n2 – объёмы выборок). В каждой выборке должно быть не более 60 наблюдений: n1, n2 60.
Слайд 33U - критерий Манна-Уитни
Рассматриваются две выборки x1,…, xn (выборка
Х) и y1,…, ym (выборка Y).Обозначим закон распределения первой выборки
через F, а второй – через G.
Нулевая гипотеза: F = G.
Альтернативная гипотеза: F G.
Возможные варианты соотношений рядов значений в двух выборках; штриховкой обозначены зоны наложения
Слайд 34Схема применения критерия Манна-Уитни
Объединить вместе значения для обеих групп по
степени нарастания признака.
Проранжировать значения, приписывая меньшему значению меньший ранг. Всего
рангов (n1 + n2).
Подсчитать сумму рангов значений первой выборки и сумму рангов значений второй выборки. Определить большую из двух ранговых сумм.
Слайд 36На двух группах лабораторных мышей – опытной (n1=9) и контрольной
(n2=11) – изучали воздействие на организм нового препарата. После месячных
испытаний масса тела животных, выраженная в граммах, варьировала следующим образом:
Используя критерий Манна-Уитни необходимо выяснить, показал ли эксперимент достоверные различия в массе тела животных 0,05.
Пример 4
Слайд 37Ранжированная выборка
Сумма рангов первой и второй выборки
Наблюдаемое значение критерия
Uкрит=23 для
=0,05, n1=9 и n2=11
Так как Uнабл > Uкрит , то
H0 принимается. Таким образом, разница между массой тела между опытной и контрольной группой мышей статистически недостоверна
Слайд 386.2. Т-критерий Вилкоксона
Критерий применяется для сопоставления показателей, измеренных в двух
разных условиях на одной и той же выборке. Он позволяет
установить не только направленность изменений, но и их выраженность. С его помощью можно определить, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом.
Критерий применим в тех случаях, когда признаки измерены, по крайней мере, в порядковой шкале, и сдвиги между вторым и первым замерами тоже могут быть упорядочены. Минимальный объем выборки равен 5.
Слайд 39T-критерий Вилкоксона
Суть метода: сопоставляется выраженность сдвигов в том или ином
направлениях по абсолютной величине.
Для этого нужно ранжировать все абсолютные
величины сдвигов, а потом суммировать отдельно ранги сдвигов в положительную и отрицательную стороны.
Если сдвиги происходят случайно, то суммы рангов их абсолютных значений будут примерно равны.
Если же интенсивность сдвига в одном из направлений перевешивает, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.
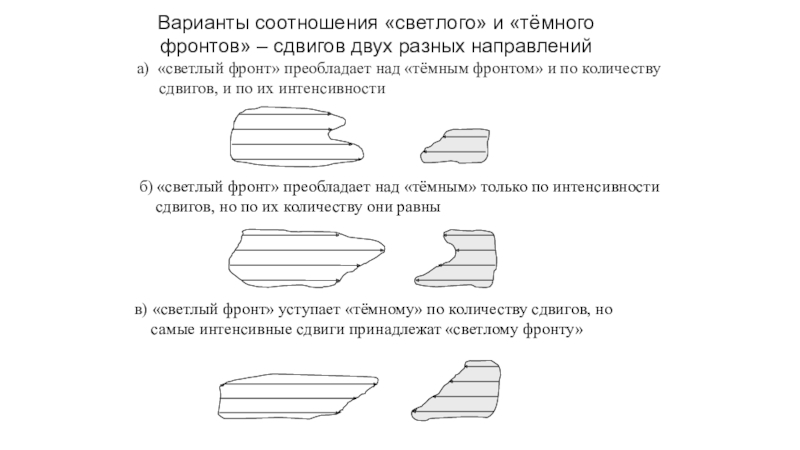
Слайд 40Варианты соотношения «светлого» и «тёмного фронтов» – сдвигов двух разных
направлений
а) «светлый фронт» преобладает над «тёмным фронтом» и по количеству
сдвигов, и по их интенсивности
б) «светлый фронт» преобладает над «тёмным» только по интенсивности сдвигов, но по их количеству они равны
в) «светлый фронт» уступает «тёмному» по количеству сдвигов, но самые интенсивные сдвиги принадлежат «светлому фронту»
Слайд 41T-критерий Вилкоксона
Формулируются гипотезы:
H0: преобладание сдвигов между начальными и конечными показателями
в одном из направлений недостоверно (значимо не отличается от нуля).
Альтернативные
гипотезы:
Ненаправленная:
H11: преобладание сдвигов между начальными и конечными показателями в одном из направлений достоверно (значимо отличается от нуля).
Направленная:
H12: интенсивность сдвигов в типичном направлении превышает интенсивность сдвигов в нетипичном направлении (значимо отличается от нуля).
Слайд 42Составить список пар в любом порядке.
Вычислить разность между индивидуальными значениями
во втором и первом замерах (после и до). Определить, что
будет считаться «типичным» сдвигом и сформулировать соответствующие гипотезы.
Перевести разности в абсолютные величины.
Проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг.
Отметить ранги, соответствующие сдвигам в «нетипичном» направлении.
Схема применения Т-критерия Вилкоксона
Слайд 44Ограничения T-критерия Вилкоксона
Минимальный объем выборки равен 5.
Нулевые сдвиги из рассмотрения
исключаются, и количество наблюдений уменьшается на количество этих нулевых сдвигов.
Можно обойти это ограничение, сформулировав гипотезы, включающие отсутствие изменений: «Сдвиг в сторону увеличения значений превышает сдвиг в сторону уменьшения значений и тенденцию сохранения их на прежнем уровне».
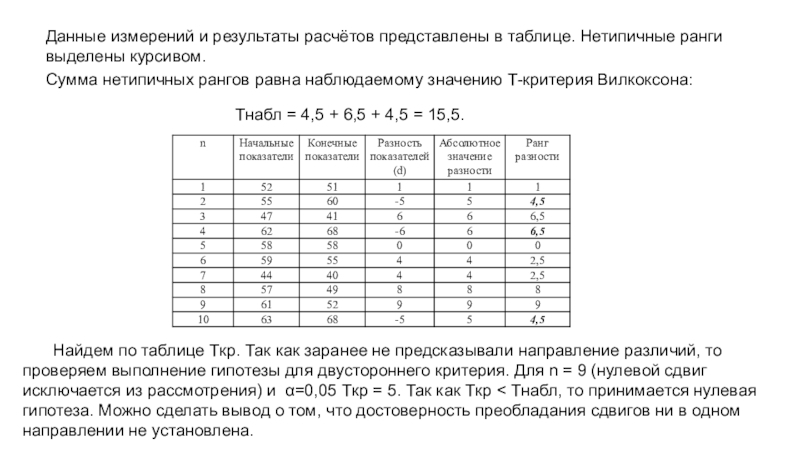
Слайд 46Данные измерений и результаты расчётов представлены в таблице. Нетипичные ранги
выделены курсивом.
Сумма нетипичных рангов равна наблюдаемому значению Т-критерия Вилкоксона:
Tнабл
= 4,5 + 6,5 + 4,5 = 15,5.
Найдем по таблице Tкр. Так как заранее не предсказывали направление различий, то проверяем выполнение гипотезы для двустороннего критерия. Для n = 9 (нулевой сдвиг исключается из рассмотрения) и α=0,05 Tкр = 5. Так как Tкр < Tнабл, то принимается нулевая гипотеза. Можно сделать вывод о том, что достоверность преобладания сдвигов ни в одном направлении не установлена.
Слайд 47Заключение
Рассмотрены основные принципы проверки статистических гипотез.
Приведены примеры проверки статистических гипотез
о параметрах генеральных совокупностей, а также о виде закона расределения.
Рассмотрены непараметрические критерии проверки гипотез: критерий Манна-Уитни и критерий Вилкоксона.
Слайд 48Литература
Анализ данных: учебник для академического бакалавриата / под. ред. В.С.Мхитаряна.
– М. : Издательство Юрайт, 2016 г. – 490 с.
Вадзинский
Р. Статистические вычисления в среде Excel. Библиотека пользователя. – СПб. : Питер, 2008. – 608 с.