Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двойной интеграл Основные понятия Геометрический смысл двойного интеграла Основные свойства двойного интеграла
Содержание
- 1. Двойной интеграл Основные понятия Геометрический смысл двойного интеграла Основные свойства двойного интеграла
- 2. Основные понятия Разобьем область D на
- 3. Основные понятияЭта сумма называется интегральной суммой функции
- 4. Основные понятияТаким образом, двойной интеграл определяется равенством:
- 5. Геометрический смысл двойного интегралаРассмотрим тело, ограниченное сверху
- 6. Геометрический смысл двойного интегралаРазобьем область D на
- 7. Объем этого цилиндра приближенно равен объему ΔVi
- 8. Свойства двойного интеграла123Если область D разбить на
- 9. Свойства двойного интеграла56Если в области D имеет
- 10. Свойства двойного интеграла8 Если функция f(x; y)
- 11. Вычисление двойного интеграла в декартовых координатахОбласть D
- 12. Пусть область D ограничена прямыми x =
- 13. Вычисление двойного интеграла в декартовых координатахФормула (1)
- 14. Пусть область D ограничена прямыми y =
- 15. Вычисление двойного интеграла в декартовых координатахВычислить D:Dy
- 16. Вычисление двойного интеграла в декартовых координатах16/17
- 17. Вычисление двойного интеграла в декартовых координатахИзменить порядок
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Двойной интеграл
Основные понятия
Геометрический смысл двойного интеграла
Основные свойства двойного интеграла
Вычисление двойного
интеграла в декартовых координатах
Слайд 2Основные понятия
Разобьем область D на n «элементарных областей»
Di,
Пусть в замкнутой области D плоскости XOY задана непрерывная
функция z = f(x, y). D
В каждой области Di выберем произвольную точку Mi(xi; yi).
Di
Mi(xi; yi).
Составим сумму вида:
площади которых обозначим через ΔSi, а диаметры (наибольшее расстояние между точками области) через di.
2/17
Слайд 3
Основные понятия
Эта сумма называется интегральной суммой функции f(x, y) в
области D.
Рассмотрим предел интегральной суммы, когда n стремится к
бесконечности, таким образом, что Если этот предел существует и не зависит от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x; y) по области D и обозначается:
3/17
Слайд 4
Основные понятия
Таким образом, двойной интеграл определяется равенством:
Функция f(x; y)
называется интегрируемой в области D,
Для всякой ли функции существует
двойной интеграл? На этот вопрос дает ответ теорема: Теорема
Если функция z = f(x; y) непрерывна в замкнутой области D, то она интегрируема в этой области (достаточное условие интегрируемости функций).
D – область интегрирования,
dxdy (или dS) – элемент площади.
x; y – переменные интегрирования,
4/17
Слайд 5Геометрический смысл двойного интеграла
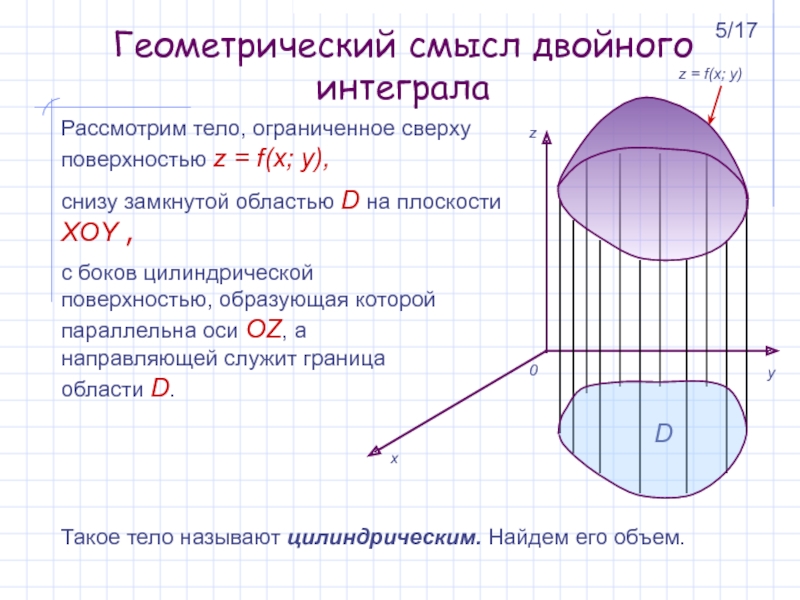
Рассмотрим тело, ограниченное сверху поверхностью z =
f(x; y),
z = f(x; y)
снизу замкнутой областью D на
плоскости XOY ,D
с боков цилиндрической поверхностью, образующая которой параллельна оси OZ, а направляющей служит граница области D.
Такое тело называют цилиндрическим. Найдем его объем.
5/17
Слайд 6
Геометрический смысл двойного интеграла
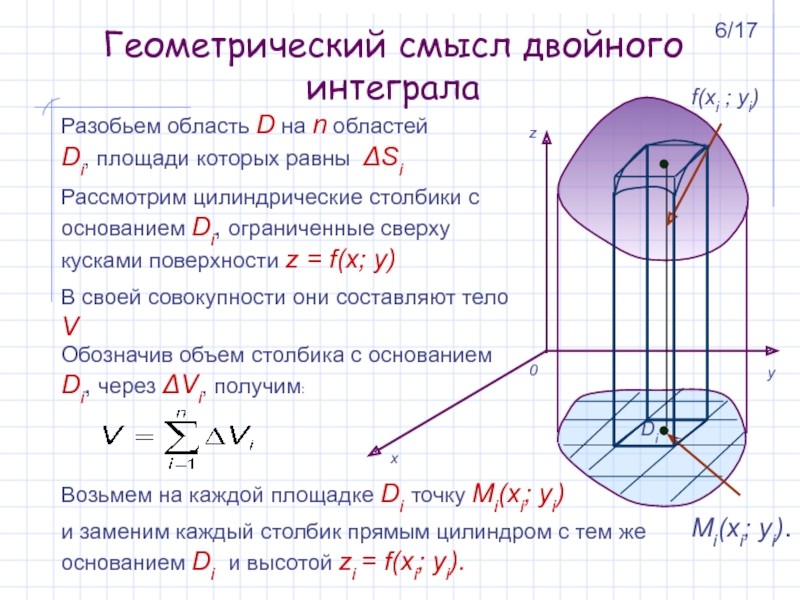
Разобьем область D на n областей Di,
площади которых равны ΔSi
Di
Рассмотрим цилиндрические столбики с основанием Di, ограниченные
сверху кусками поверхности z = f(x; y) В своей совокупности они составляют тело V
Обозначив объем столбика с основанием Di, через ΔVi, получим:
Возьмем на каждой площадке Di точку Mi(xi; yi)
Mi(xi; yi).
и заменим каждый столбик прямым цилиндром с тем же основанием Di и высотой zi = f(xi; yi).
f(xi ; yi)
6/17
Слайд 7Объем этого цилиндра приближенно равен объему ΔVi цилиндрического столбика
Тогда
получаем:
Это равенство тем точнее, чем больше число n и
чем меньше размеры элементарных областей, поэтому:Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Геометрический смысл двойного интеграла
7/17
Слайд 8Свойства двойного интеграла
1
2
3
Если область D разбить на две области D1
и D2 не имеющих общих точек, то
4
8/17
Слайд 9Свойства двойного интеграла
5
6
Если в области D имеет место неравенство:
Если
в области D функции f(x; y) и g(x; y) удовлетворяют
неравенству:7
Если функция f(x; y) непрерывна в замкнутой области D, площадь которой S то:
где m и M соответственно наименьшее и наибольшее значение подынтегральной функции в области D.
9/17
Слайд 10Свойства двойного интеграла
8
Если функция f(x; y) непрерывна в замкнутой
области D, площадь которой S, то в этой области существует
такая точка (x0 ; y0), чтоВеличину
называют средним значением функции f(x ; y) в области D.
10/17
Слайд 11
Вычисление двойного интеграла в декартовых координатах
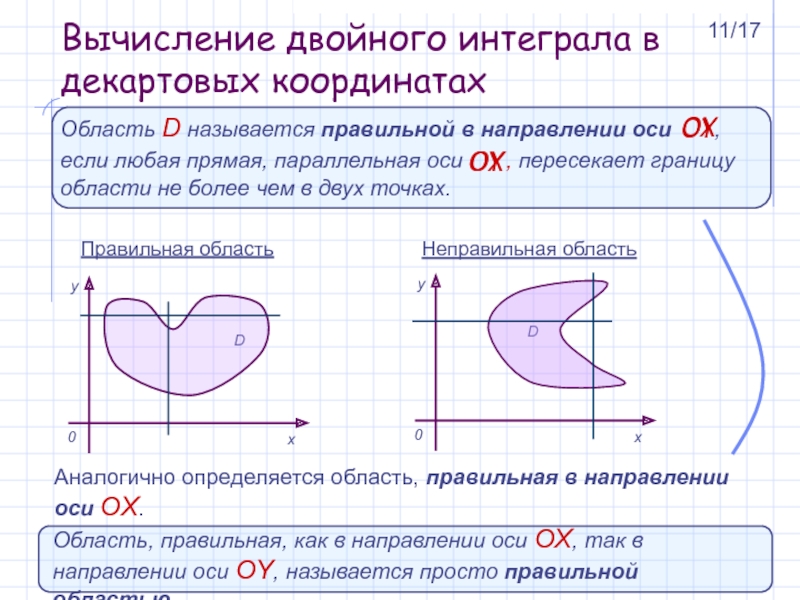
Область D называется правильной в
направлении оси , если любая прямая, параллельная оси
, пересекает границу области не более чем в двух точках.Правильная область
Неправильная область
Аналогично определяется область, правильная в направлении оси OX.
Область, правильная, как в направлении оси OX, так в направлении оси OY, называется просто правильной областью.
ОY
ОX
ОY
ОX
11/17
Слайд 12
Пусть область D ограничена прямыми x = a, x =
b (a < b) и кривыми y = φ1(x), y
= φ2(x), причем функции φ1(x) и φ2(x) непрерывны и таковы, чтоТаким образом задается область, правильная в направлении оси OY.
D
y =
b
a
y =
(1)
Вычисление двойного интеграла в декартовых координатах
a
b
φ2(x)
φ1(x)
φ1(x)
φ2(x)
12/17
Слайд 13
Вычисление двойного интеграла в декартовых координатах
Формула (1) представляет собой способ
вычисления двойного интеграла в декартовых координатах.
Правую часть формулы (1)
называют двукратным (или повторным) интегралом от функции f(x, y) по области D. (1)
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая x постоянным,
затем берем внешний интеграл, то есть результат первого интегрирования интегрируем по x в пределах от a до b.
13/17
Слайд 14
Пусть область D ограничена прямыми y = c, y =
d (c < d) и кривыми x = ψ1(y), x
= ψ2(y), причем функции ψ1(y) и ψ2(y) непрерывны и таковы, чтоТаким образом задается область, правильная в направлении оси OX.
D
x =
d
c
x =
(2)
Вычисление двойного интеграла в декартовых координатах
c
d
ψ2(x)
ψ1(x)
ψ1(x)
ψ2(x)
14/17
Слайд 15
Вычисление двойного интеграла в декартовых координатах
Вычислить
D:
D
y = x2
y =
2 - x
Воспользуемся формулой (2)
15/17
0
1
x = 2 - y
2
- yСлайд 17
Вычисление двойного интеграла в декартовых координатах
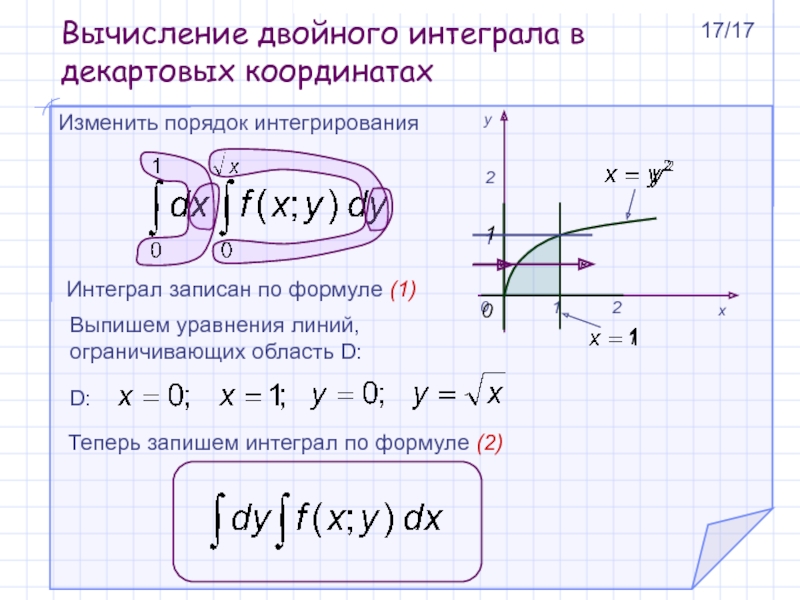
Изменить порядок интегрирования
D:
Интеграл записан по
формуле (1)
17/17
Выпишем уравнения линий, ограничивающих область D:
Теперь запишем
интеграл по формуле (2) 0
1
1