Слайд 1Методы оптимизации
6.ДВОЙСТВЕННОСТЬ И АНАЛИЗЧУВСТВИТЕЛЬНОСТИ
Слайд 26.1. ОПРЕДЕЛЕНИЕ ДВОЙСТВЕННОЙ ЗАДАЧИ
Исходную задачу линейного программирования
будем называть прямой. Двойственная задача — это задача, формулируемая с
помощью определенных правил непосредственно из прямой задачи. В этом разделе рассмотрены правила построения двойственных задач.
Часто рассматривают формулировки двойственной задачи в зависимости от различных видов прямой задачи, которые определяются типами ограничений, знаками переменных (неотрицательные или свободные, т.е. без ограничения в знаке) и типом оптимизации (максимизация или минимизация целевой функции), что не всегда оправдано. Приведем единую формулировку двойственной задачи, применимую ко всем видам прямой задачи. В основу такой формулировки положена стандартная форма прямой задачи. Напомним, что задача ЛП в стандартной форме записывается следующим образом.
Максимизировать или минимизировать целевую функцию
при ограничениях
Слайд 3 В состав n переменных xj, входят
также дополнительные переменные. Стандартная форма задачи ЛП предполагает выполнение следующих
условий.
1. Все ограничения записаны в виде равенств (с неотрицательной правой частью).
2. Все переменные неотрицательны.
3. Оптимизация определяется как максимизация или минимизация целевой функции.
Стандартная форма задачи ЛП порождает стандартную таблицу симплекс-метода. Поэтому, как будет показано в разделе 4.3, решение двойственной задачи можно получить непосредственно из симплекс-таблицы, соответствующей оптимальному решению прямой задачи. Таким образом, определив двойственную задачу на основе стандартной формы прямой задачи, после вычислений симплекс-метода мы автоматически получаем решение двойственной задачи.
Переменные и ограничения двойственной задачи формируются путем симметричных структурных преобразований прямой задачи по следующим правилам.
1. Каждому из m ограничений прямой задачи соответствует переменная двойственной задачи.
2. Каждой из n переменных прямой задачи соответствует ограничение двойственной задачи.
3. Коэффициенты при какой-либо переменной в ограничениях прямой задачи становятся коэффициентами ограничения двойственной задачи, соответствующей этой переменной, а правая часть формируемого ограничения равна коэффициенту при этой переменной в выражении целевой функции.
4. Коэффициенты целевой функции двойственной задачи равны правым частям ограничений прямой задачи.

Слайд 4
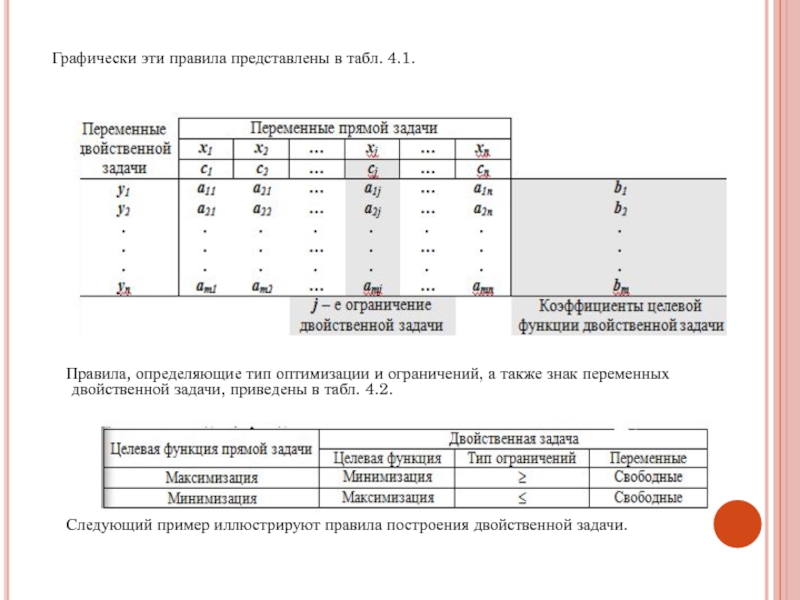
Графически эти правила представлены в табл. 4.1.
Правила,
определяющие тип оптимизации и ограничений, а также знак переменных двойственной
задачи, приведены в табл. 4.2.
Следующий пример иллюстрируют правила построения двойственной задачи.
Слайд 5 Пример 4.2-3
Двойственная задача
Минимизировать w =
5y1 + 3y2 + 8у3
при ограничениях
y1 – y2 + 4y3 = 5,
2у1 + 5y2 + 7у3 ≥ 6,
-y2 ≥ 0 → y2 ≤ 0,
y3 ≥ 0,
у1 — свободная переменная,
y2, y3 — свободные переменные (избыточное условие).
Первое и второе ограничения двойственной задачи заменены одним ограничением в виде равенства. Здесь действует следующее правило: свободной переменной прямой задачи соответствует ограничение в виде равенства двойственной задачи и, наоборот, ограничению в виде равенства прямой задачи соответствует свободная переменная двойственной задачи.
Слайд 66.2. СООТНОШЕНИЯ МЕЖДУ ОПТИМАЛЬНЫМИ РЕШЕНИЯМИ ПРЯМОЙ И ДВОЙСТВЕННОЙ ЗАДАЧ
Прямая и двойственная задачи так тесно взаимосвязаны, что оптимальное
решение одной задачи можно получить непосредственно (без дополнительных вычислений) из симплекс-таблицы, представляющей оптимальное решение другой. Это утверждение основывается на следующем соотношении.
Соотношение 1. Для любой симплекс - итерации прямой или двойственной задачи.
Это соотношение симметрично относительно прямой и двойственной задач. Его можно использовать для определения оптимального решения одной задачи непосредственно из симплекс-таблицы, содержащей оптимальное решение другой. Данное обстоятельство обуславливает возможность проведения вычислений именно по той задаче (прямой или двойственной), которая требует меньших вычислительных ресурсов. Например, если прямая задача имеет 100 переменных и 500 ограничений, то предпочтительнее нахождение оптимального решения двойственной задачи, так как она будет содержать только 100 ограничений
Слайд 7Пример 4.3-1
Рассмотрим прямую и двойственную задачи из примера 4.2-1
В следующей
таблице представлены симплекс-итерации решения прямой задачи
Применяя на третьей симплекс -
итерации соотношение 1 для переменных x4 и R из начального базисного решения, получим следующие данные
Слайд 8 Решениями полученных уравнений будут у1 = 29/5
и у2 = -2/5. Если бы решения двойственной задачи искались
независимо от решения прямой задачи, то было бы получено такое же решение. Аналогично, вследствие симметричности соотношения 1, из данного решения двойственной задачи и ее начальной симплекс-таблицы получаем оптимальное решение прямой задачи: x1 = 26/5, x2 = 12/5 и x3 = 0. (Решите двойственную задачу и убедитесь, что ее решение действительно совпадает с приведенным выше.)
Применение соотношения 1 к переменным начального решения всегда приводит к легко решаемым уравнениям, так как каждое такое уравнение содержит только одну переменную. Конечно же, ничего не мешает использовать другие переменные (такие, как x1, х2 и х3 в рассматриваемой задаче) при построении уравнений, необходимых для определения значений переменных двойственной задачи. Например, соотношение 1 порождает следующие уравнения, ассоциируемые с переменными x1 и x3:
y1 + 2у2 - 5 = 0,
y1 + 3у2 - 4 = 3/5.
Решение этой системы уравнений также приводит к оптимальным значениям двойственной задачи у1 = 29/5 и у2 = -2/5. Однако аналогичные уравнения, ассоциируемые с переменными х4 и R, будут уже не так просты. (Убедитесь самостоятельно, что уравнения, ассоциированные с любыми двумя переменными из множества x1, x2, x3, x4, R, дают одни и те же значения переменных двойственной задачи.)
Представим еще одно соотношение между прямой и двойственной задачами, которое совместно с соотношением 1 предлагает интересную экономическую интерпретацию задачи линейного программирования.
Соотношение 2. Для любой пары допустимых решений прямой и двойственной задачи
В точке оптимума это соотношение принимает вид строгого равенства.

Слайд 9 Пример 4.3-2
В примере
4.3-1 нетрудно показать (путем подстановки в ограничения), что прямая и
двойственная задачи имеют допустимые решения х1 = 0, х2 = 0, х3 = 8/3 и y1 = 6, y2 = 0. Для этих решений значения целевых функций соответственно равны z = 32/3 и w = 60. Для оптимальных решений х1 = 26/5, х2 = 12/5, х3 = 0 и у1 = 29/5, у2 = -2/5 имеем z = w = 54,8. Таким образом, приведенные значения целевых функций подтверждают соотношение 2.
Из соотношения 2 следует, что для всех допустимых решений прямой и двойственной задач значения целевой функции задачи минимизации всегда будут верхним пределом значений целевой функции задачи максимизации. Таким образом, итерационное решение задачи максимизации ведет к возрастанию значений целевой функции, а итерационное решение задачи минимизации — к ее убыванию. В итоге, при успешном завершении процессов вычисления прямой и двойственной задач приходим к точке "равновесия", где значения целевых функций задач максимизации и минимизации становятся равными.
Слайд 106.3. ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД
В двойственном симплекс-методе решение задачи
ЛП начинается с недопустимого, но лучшего, чем оптимальное решение. Последовательные
итерации этого метода приближают решение к области допустимости без нарушения оптимальности (точнее, "супероптимальности") промежуточных решений. Когда будет достигнута область допустимых решений, процесс вычислений заканчивается, так как последнее решение будет оптимальным. Очевидно, что он значительно отличается от обычного (прямого) симплекс-метода, рассмотренного в главе 3, где начальное решение всегда допустимое, но не оптимальное, и промежуточные решения никогда не выходят из пространства допустимых решений.
В двойственном симплекс-методе начальная симплекс-таблица обязательно должна иметь в базисном решении недопустимую (т.е. отрицательную) переменную. Для реализации двойственного симплекс-метода разработаны следующие два условия, выполнение которых гарантирует оптимальность последовательных промежуточных решений и приближение их к области допустимых решений.
Двойственное условие допустимости. В качестве исключаемой переменной хr выбирается базисная переменная, имеющая наибольшее по абсолютной величине отрицательное значение. Если таких переменных несколько, то выбор произволен. Если все базисные переменные неотрицательные, процесс вычислений заканчивается.

Слайд 11 Двойственное условие оптимальности. Вводимая в базис переменная определяется
как переменная, на которой достигается следующий минимум:
,
где αrj — коэффициент из симплекс-таблицы, расположенный на пересечении ведущей строки (соответствующей исключаемой переменной хr) и столбца, соответствующего переменной xj. При наличии нескольких альтернативных переменных, выбор делается произвольно.
Двойственное условие оптимальности основывается на той же основной идее, что и условие оптимальности прямого симплекс-метода из главы 3.
Пример 4.5-1
Дана следующая задача ЛП.
Минимизировать z = 3x1 + 2х2
при ограничениях
3x1 + x2 ≥ 3,
4х1 + 3x2 ≥ 6,
xl +x2 ≤ 3,
x1, x2 ≥ 0.
Начальная симплекс-таблица этой задачи имеет следующий вид
Слайд 12 Среди дополнительных переменных этой задачи, x3
и x4 являются избыточными, а x5 — остаточной. Мы умножили
каждое равенство, соответствующее избыточным дополнительным переменным, на -1; в результате правые части этих равенств непосредственно указывают на базисные переменные, которые являются недопустимыми (x3 = -3, х4 = -6, х5 = 3). Этот подход всегда используется при реализации двойственного симплекс-метода. Поскольку zj – сj ≤ 0 для всех j = 1, …, 5, начальное базисное решение является оптимальным (но не допустимым). Таким образом, приведенная таблица удовлетворяет требованиям начальной таблицы двойственного симплекс-метода, а именно — оптимальности и недопустимости.
Двойственное условие допустимости указывает на переменную х4 (= -6) как на вводимую в базис. Теперь применим двойственное условие оптимальности для определения исключаемой переменной. Для этого используем следующую таблицу
Приведенные отношения показывают, что исключаемой переменной будет х2. Отметим, что переменные хj будут кандидатами на исключение из базисного решения только тогда, когда коэффициент α4j будет строго отрицательным. По этому критерию переменные x3, х4 и х5 не рассматриваются как кандидаты на исключение из базиса.
Следующая таблица получена с помощью известных операций над строками, применяемых в прямом симплекс-методе

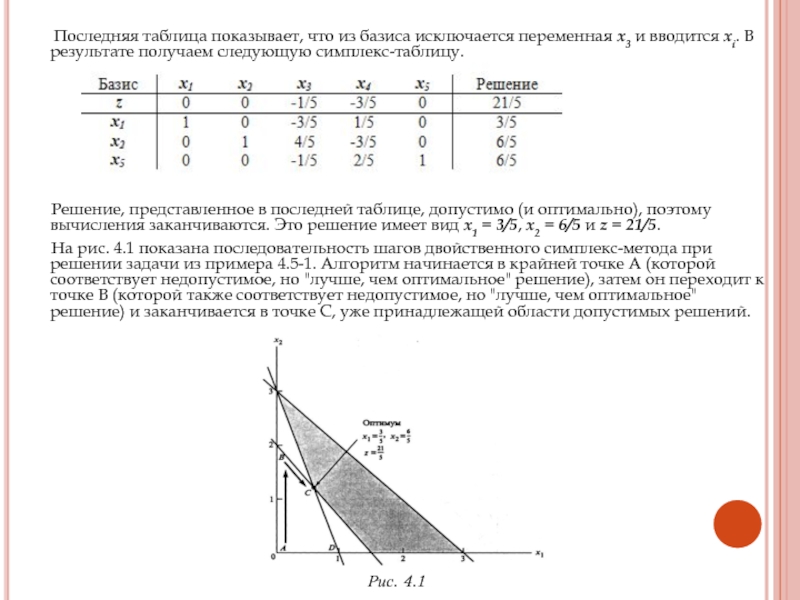
Слайд 13 Последняя таблица показывает, что из базиса исключается
переменная х3 и вводится xi. В результате получаем следующую симплекс-таблицу.
Решение, представленное в последней таблице, допустимо (и оптимально), поэтому вычисления заканчиваются. Это решение имеет вид x1 = 3/5, х2 = 6/5 и z = 21/5.
На рис. 4.1 показана последовательность шагов двойственного симплекс-метода при решении задачи из примера 4.5-1. Алгоритм начинается в крайней точке А (которой соответствует недопустимое, но "лучше, чем оптимальное" решение), затем он переходит к точке В (которой также соответствует недопустимое, но "лучше, чем оптимальное" решение) и заканчивается в точке С, уже принадлежащей области допустимых решений.
Рис. 4.1