Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двугранный угол
Содержание
- 1. Двугранный угол
- 2. ПланиметрияСтереометрияУглом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.Двугранный угол
- 3. Двугранным углом называется фигура, образованная прямой a
- 4. Угол РDEK Двугранный угол АВNМ, где ВN
- 5. Угол РОК – линейный угол двугранного угла
- 6. Все линейные углы двугранного угла равны друг
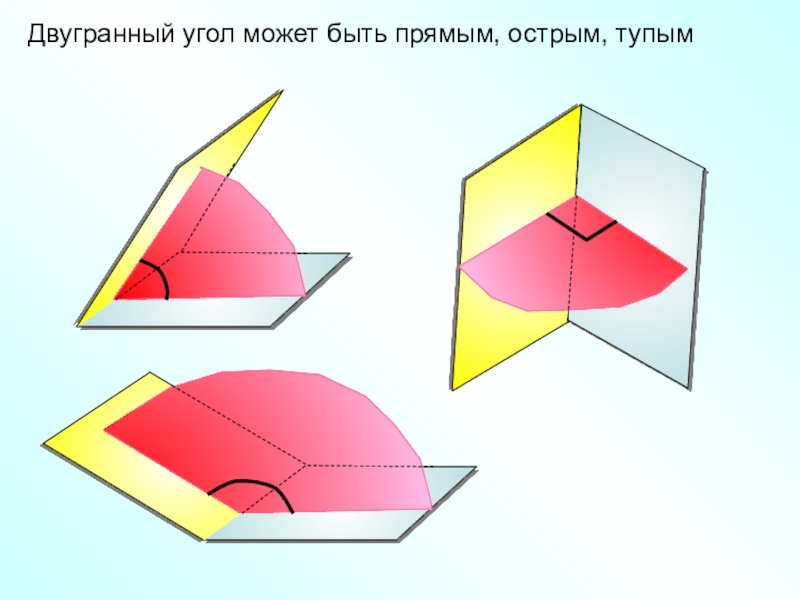
- 7. Двугранный угол может быть прямым, острым, тупым
- 8. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – равнобедренный.АСВП-рН-яП-яУгол ВMN – линейный угол двугранного угла ВАСКК
- 9. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – прямоугольный.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВАСККС
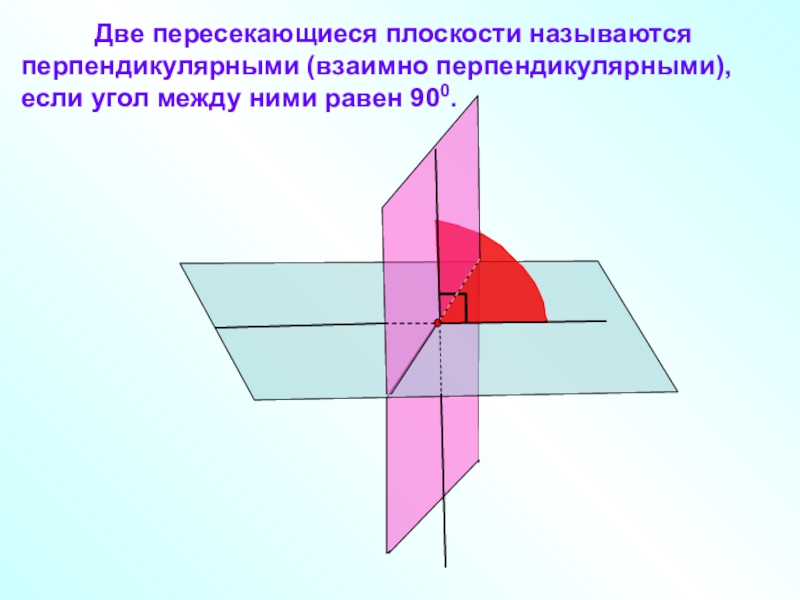
- 10. Две пересекающиеся
- 11. Примером
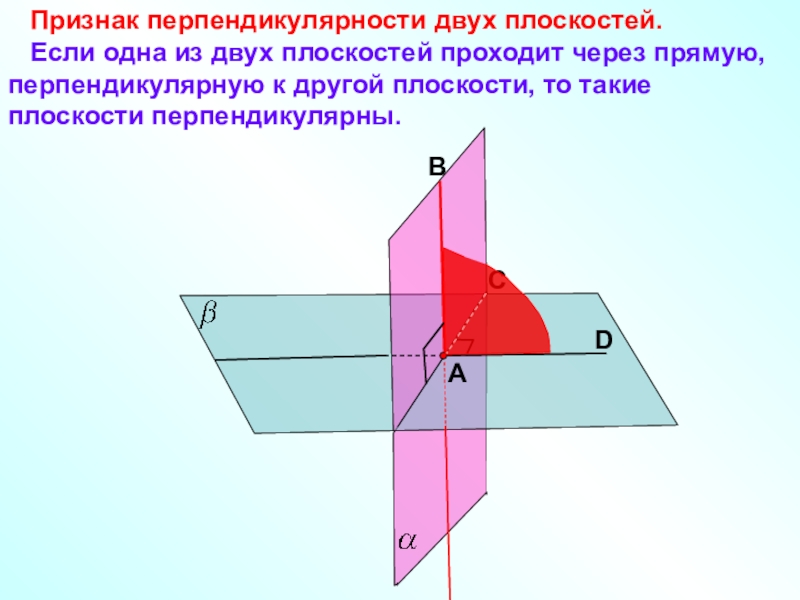
- 12. Признак перпендикулярности двух плоскостей.
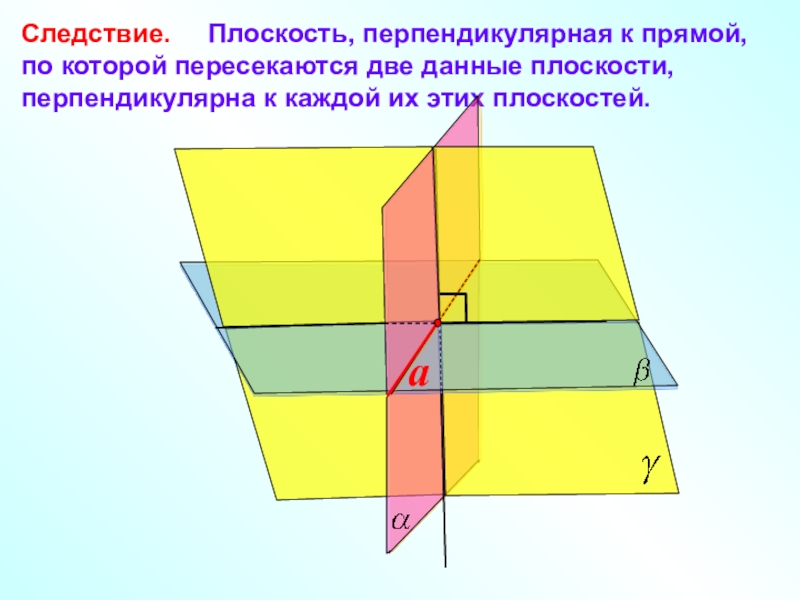
- 13. Следствие. Плоскость, перпендикулярная к прямой,
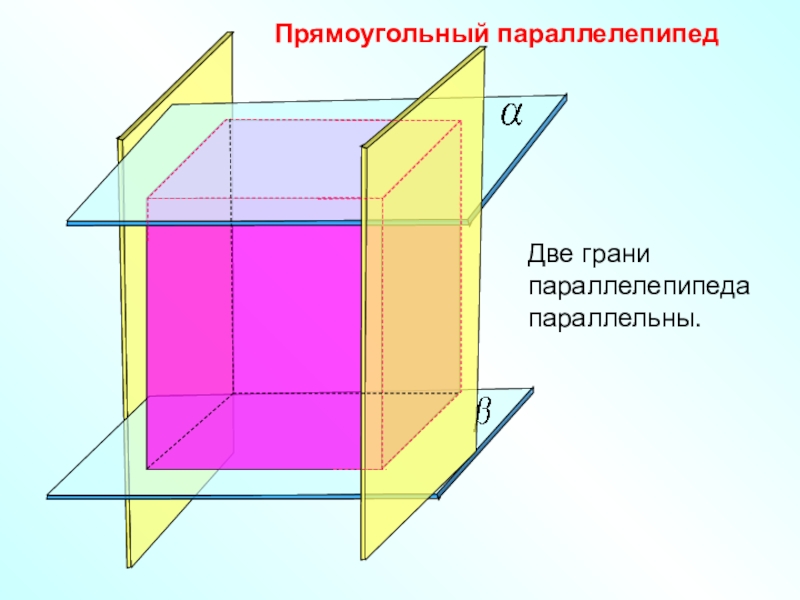
- 14. Прямоугольный параллелепипедДве грани параллелепипеда параллельны.
- 15. 10. В прямоугольном параллелепипеде все
- 16. ПланиметрияСтереометрияВ прямоугольнике квадрат диагонали равен сумме квадратов
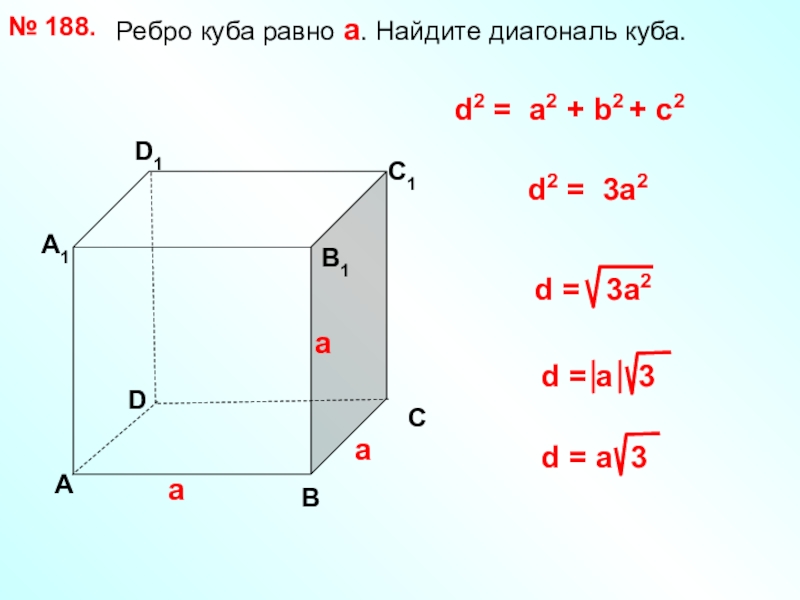
- 17. Ребро
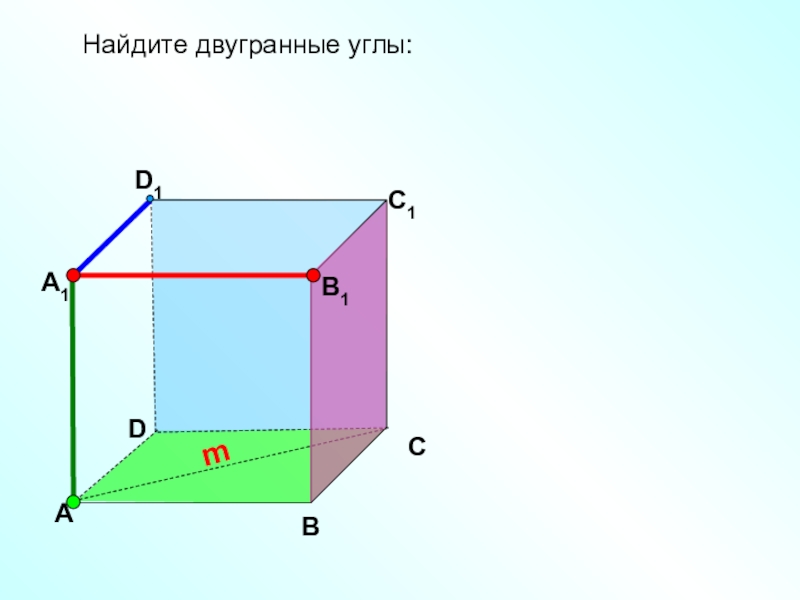
- 18. Найдите двугранные углы:DАВСD1С1mВ1А1
- 19. Дан
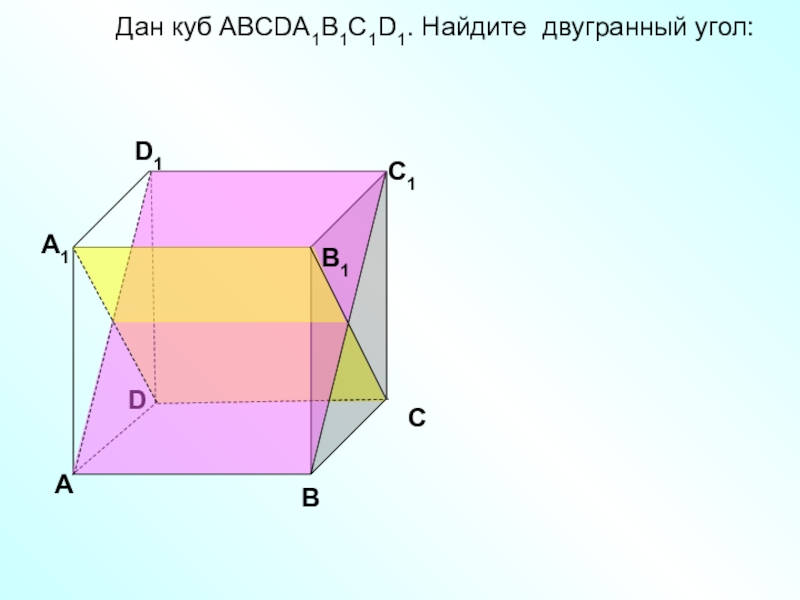
- 20. Дан куб АВСDА1В1С1D1. Найдите двугранный угол: DАВСА1D1С1В1
- 21. Найдите
- 22. DАВСА1D1С1В11. Найдите угол А1ВС12. Доказать, что MN
- 23. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – тупоугольный.АВП-рН-яП-яУгол ВSN – линейный угол двугранного угла ВАСККС
- 24. Построить линейный угол двугранного угла ВDСК.АВСD – прямоугольник.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВDСККСD
- 25. Построить линейный угол двугранного угла ВDСК.АВСD –
- 26. Построить линейный угол двугранного угла ВDСК.АВСD –
- 27. Построить линейный угол двугранного угла ВDСК.АВСD –
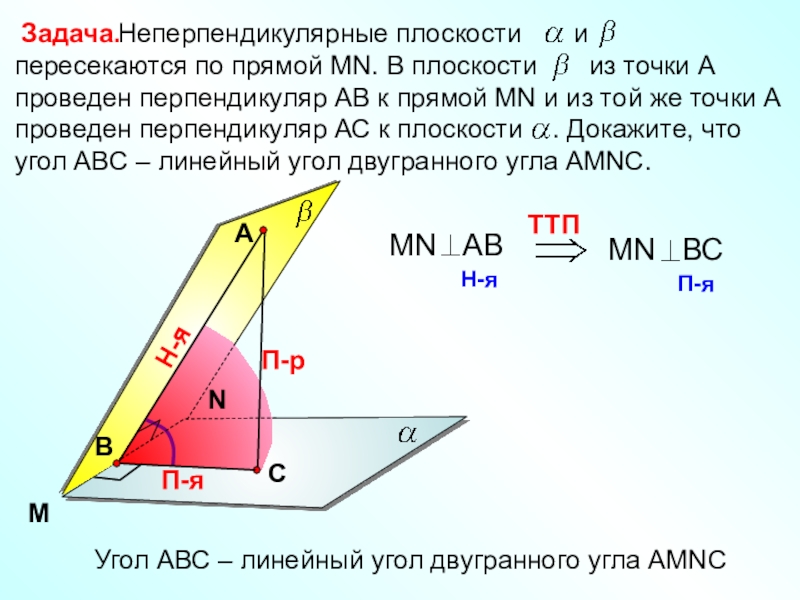
- 28. Задача.MNАП-рН-яП-яУгол АВС – линейный угол двугранного угла АМNC
- 29. САВDM
- 30. Слайд 30
- 31. Слайд 31
- 32. Домашнее заданиеГлава 3 п. 4 с 138-144Задача 5, 6 с. 146 (419, 420 электронный учебник)
- 33. Скачать презентанцию
ПланиметрияСтереометрияУглом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.Двугранный угол
Слайды и текст этой презентации
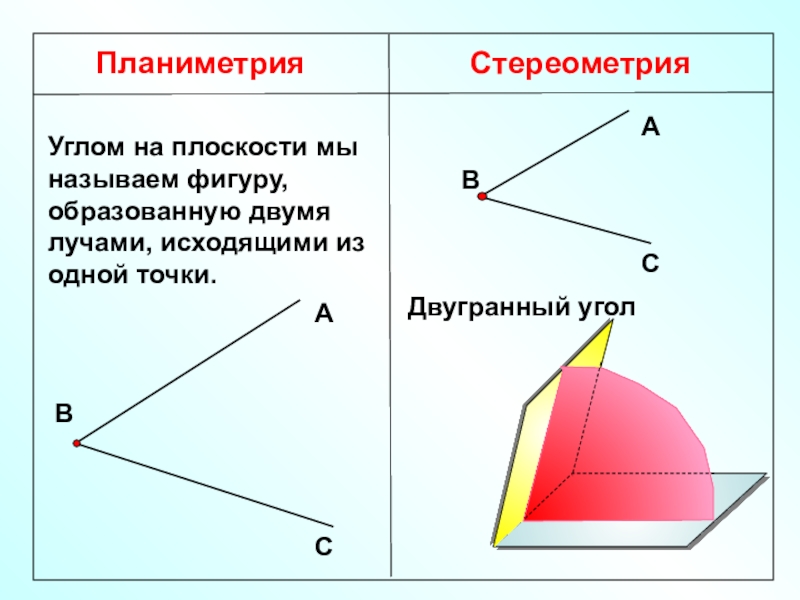
Слайд 2Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими
из одной точки.
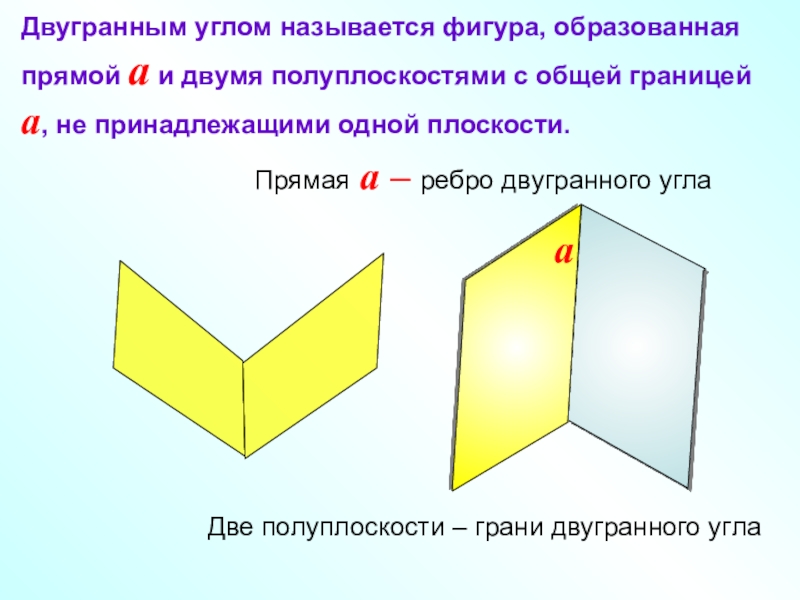
Слайд 3Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями
с общей границей a, не принадлежащими одной плоскости.
Две полуплоскости –
грани двугранного углаПрямая a – ребро двугранного угла
a
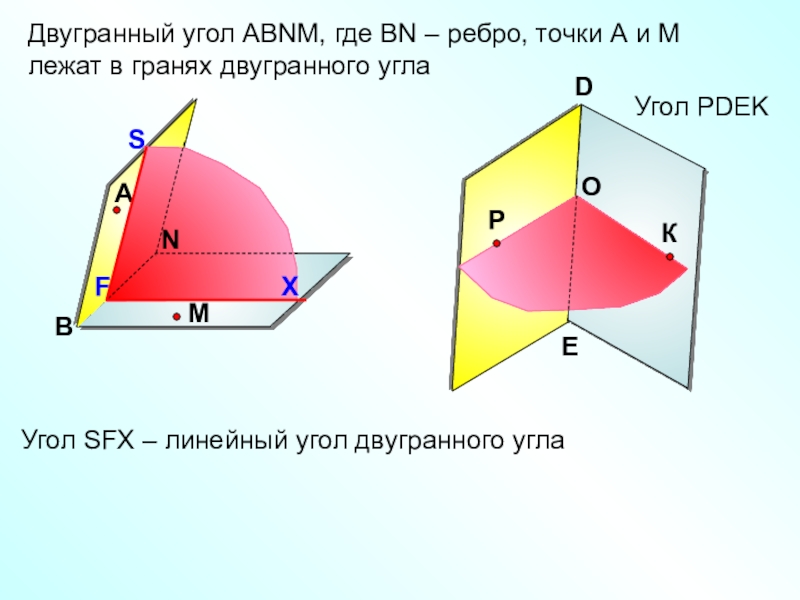
Слайд 4Угол РDEK
Двугранный угол АВNМ, где ВN – ребро, точки
А и М лежат в гранях двугранного угла
А
В
N
Р
M
К
D
E
Угол SFX –
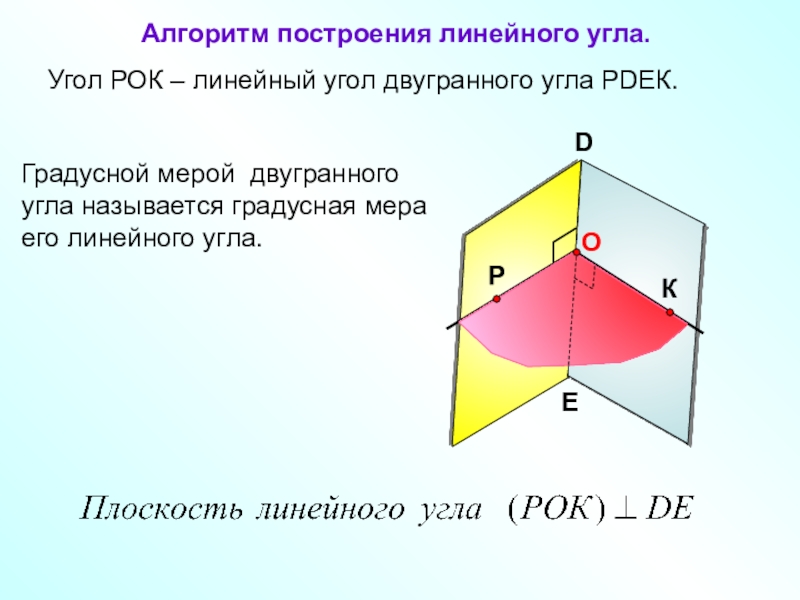
линейный угол двугранного угла
Слайд 5Угол РОК – линейный угол двугранного угла РDEК.
D
E
Градусной мерой двугранного
угла называется градусная мера его линейного угла.
Алгоритм построения линейного угла.
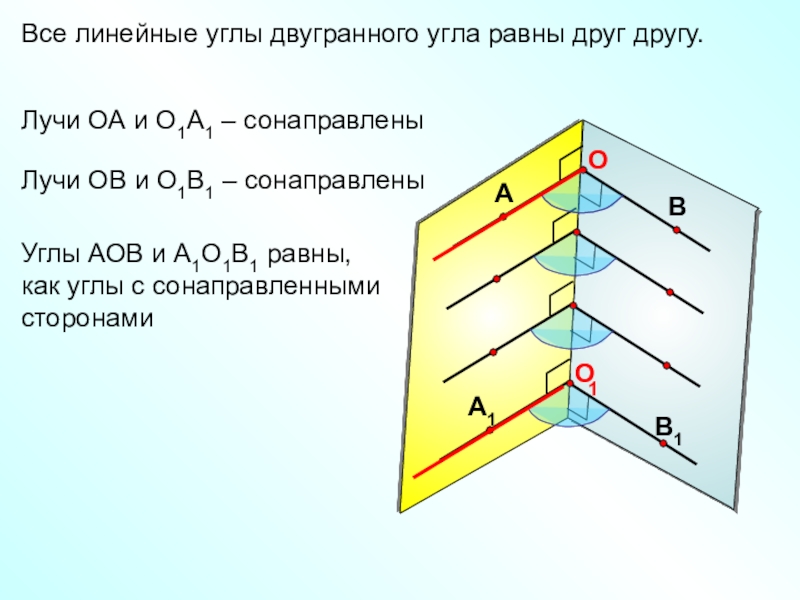
Слайд 6Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и
О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы
АОВ и А1О1В1 равны, как углы с сонаправленными сторонами
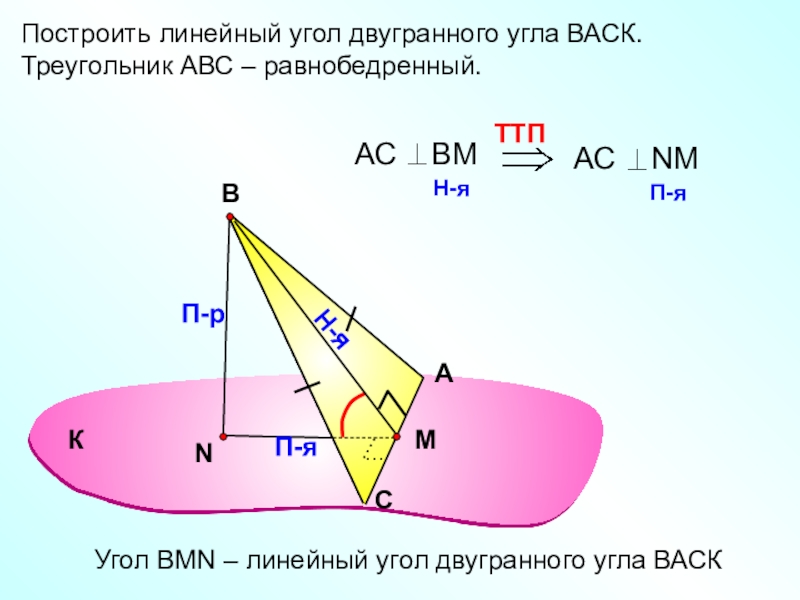
Слайд 8Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN
– линейный угол двугранного угла ВАСК
К
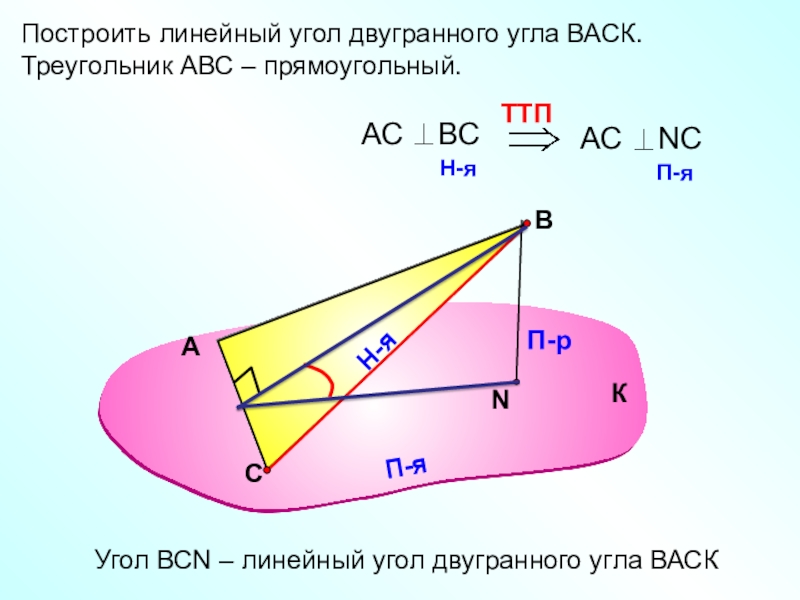
Слайд 9Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN
– линейный угол двугранного угла ВАСК
К
С
Слайд 10 Две пересекающиеся плоскости называются перпендикулярными
(взаимно перпендикулярными), если угол между ними равен 900.
Слайд 11 Примером взаимно перпендикулярных плоскостей
служат плоскости стены и пола комнаты,
плоскости стены и потолка.
Слайд 12 Признак перпендикулярности двух плоскостей.
Если одна из двух плоскостей проходит через прямую,
перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.А
С
Слайд 13Следствие. Плоскость, перпендикулярная к прямой,
по которой пересекаются
две данные плоскости, перпендикулярна к каждой их этих плоскостей.
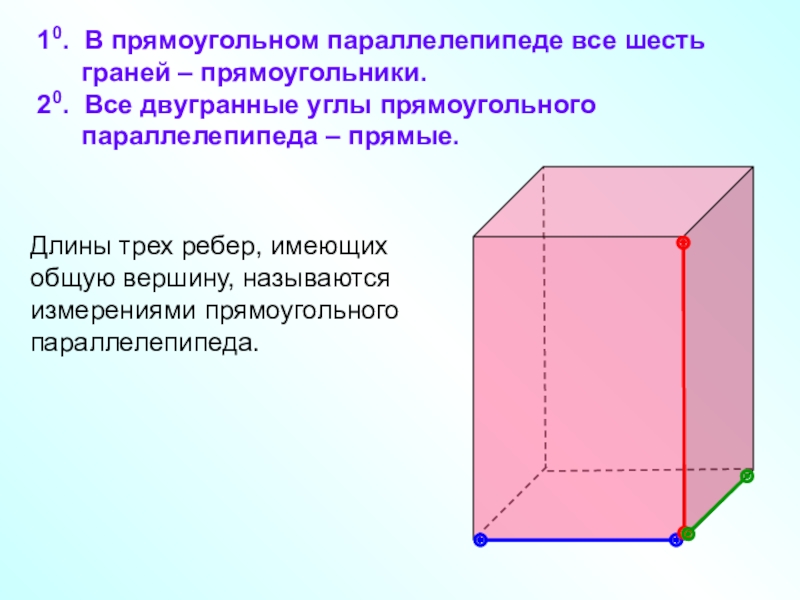
Слайд 15 10. В прямоугольном параллелепипеде все шесть
граней – прямоугольники.
20. Все
двугранные углы прямоугольного параллелепипеда – прямые.
Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.
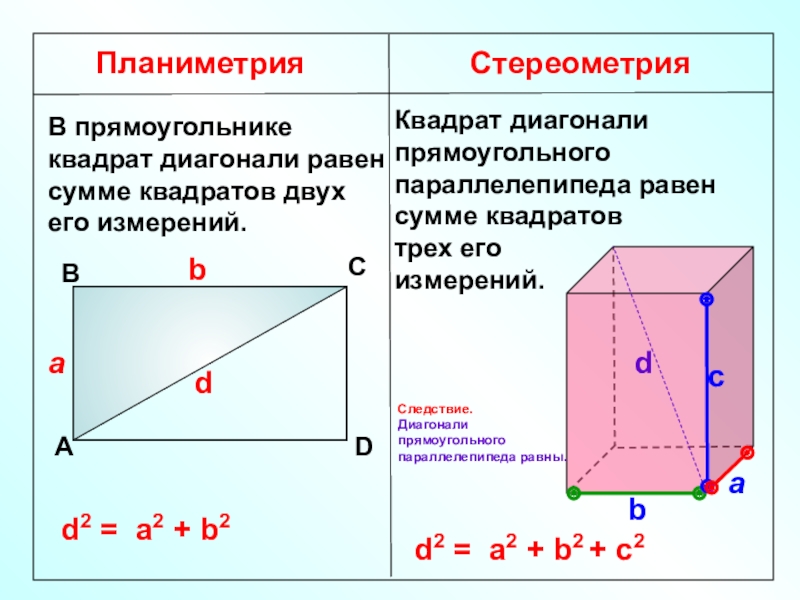
Слайд 16Планиметрия
Стереометрия
В прямоугольнике квадрат диагонали равен сумме квадратов двух его измерений.
А
В
С
D
d
a
b
d2
= a2 + b2
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов
трех его
измерений.
d2 = a2 + b2 + с2
Следствие.
Диагонали прямоугольного
параллелепипеда равны.
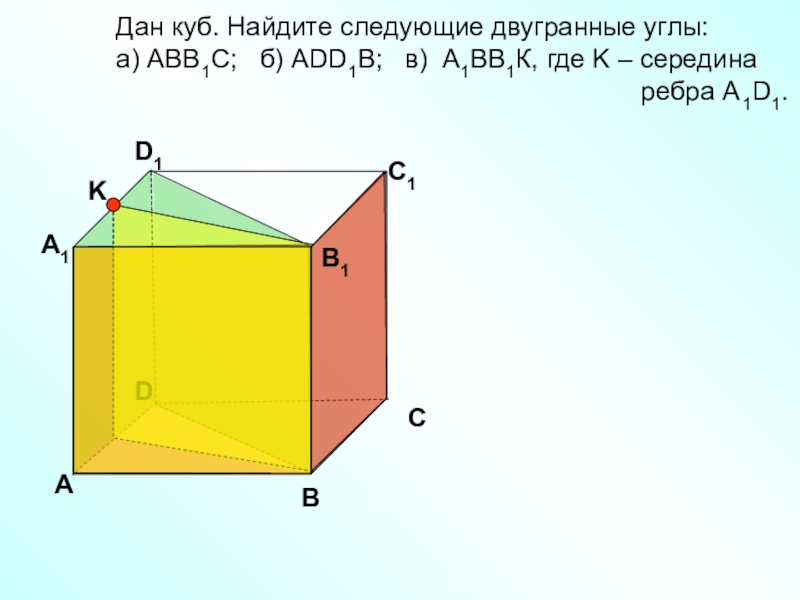
Слайд 19 Дан куб. Найдите следующие
двугранные углы:
a) АВВ1С;
б) АDD1B; в) А1ВВ1К, где K – серединаребра А1D1.
D
А
В
С
А1
D1
С1
В1
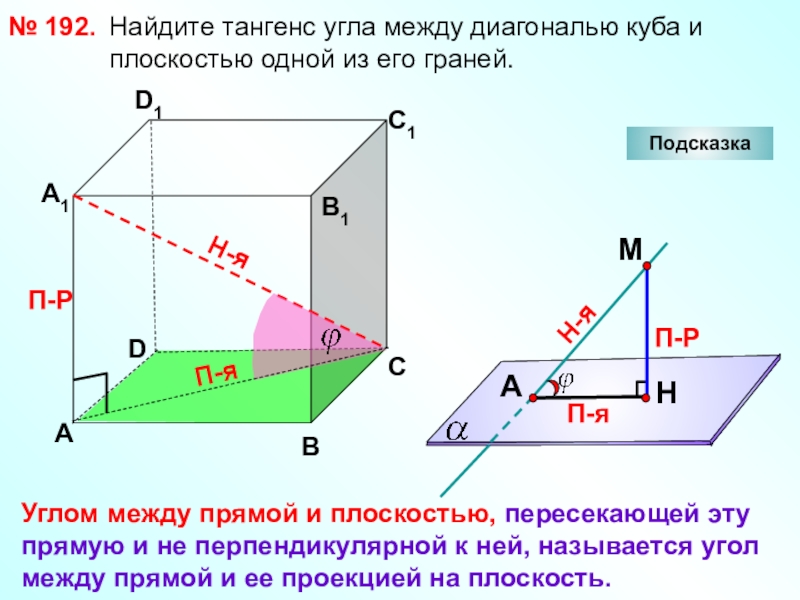
Слайд 21 Найдите тангенс угла между
диагональю куба и
плоскостью одной
из его граней.№ 192.
D
А
В
С
А1
D1
С1
В1
Подсказка
П-Р
Н-я
Слайд 22D
А
В
С
А1
D1
С1
В1
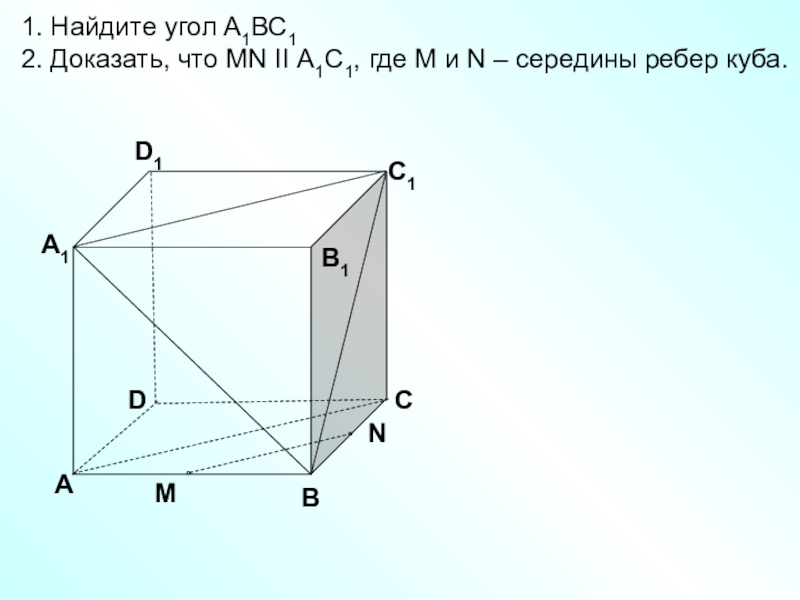
1. Найдите угол А1ВС1
2. Доказать, что MN II А1С1, где
M и N – середины ребер куба.
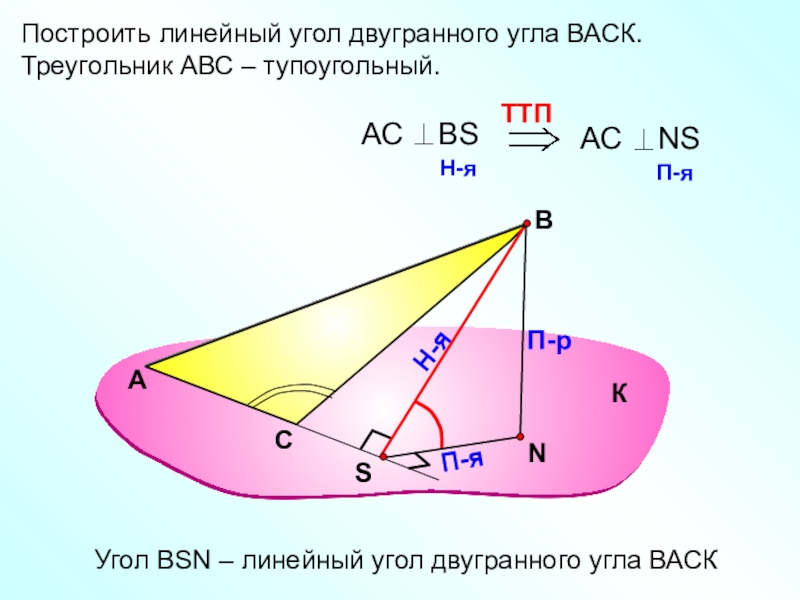
Слайд 23Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN
– линейный угол двугранного угла ВАСК
К
С
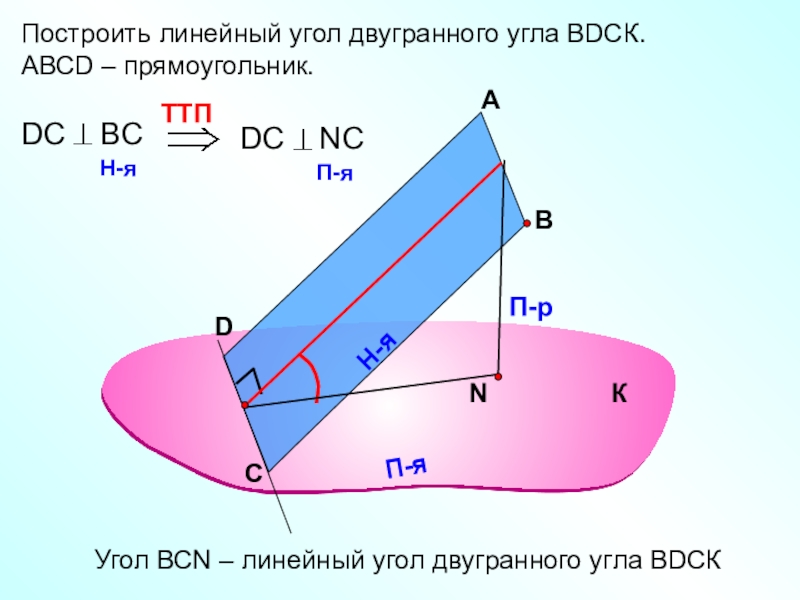
Слайд 24Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
П-р
Н-я
П-я
Угол ВСN –
линейный угол двугранного угла ВDСК
К
С
D
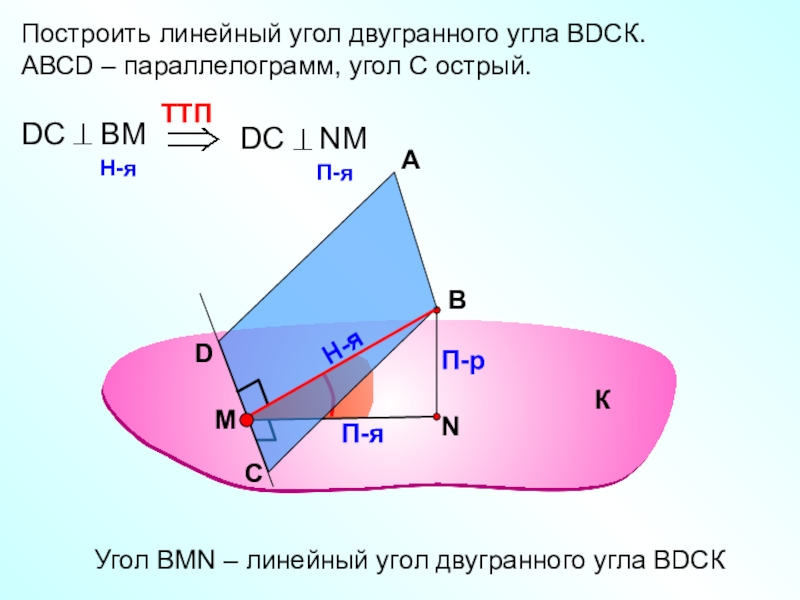
Слайд 25Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С
острый.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
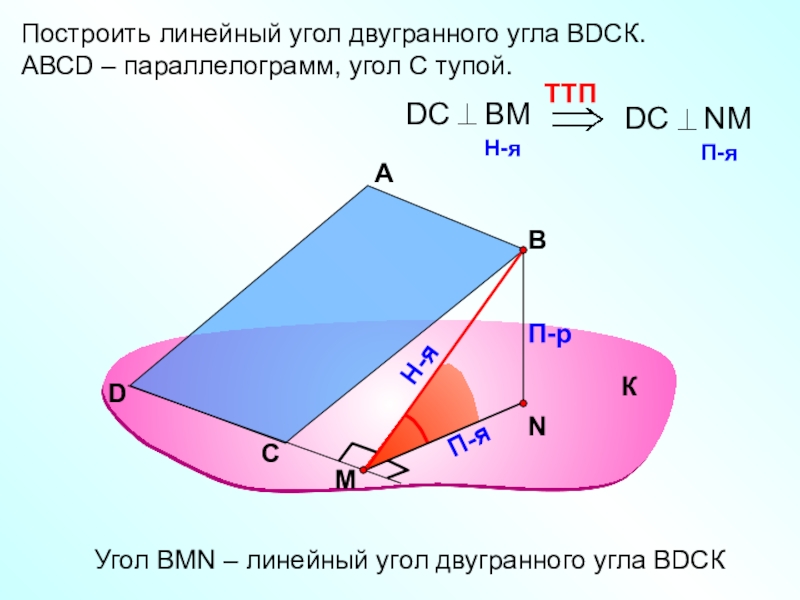
Слайд 26Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С
тупой.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
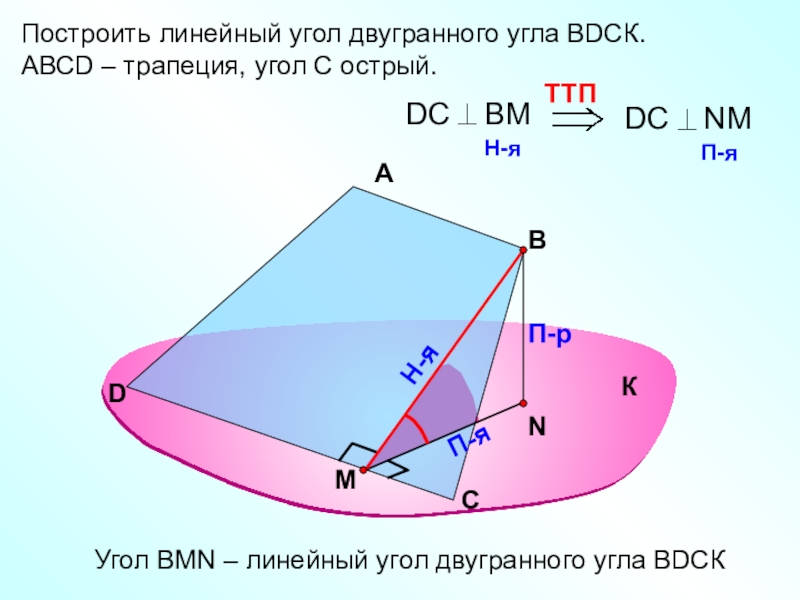
Слайд 27Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С
острый.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 29С
А
В
D
M
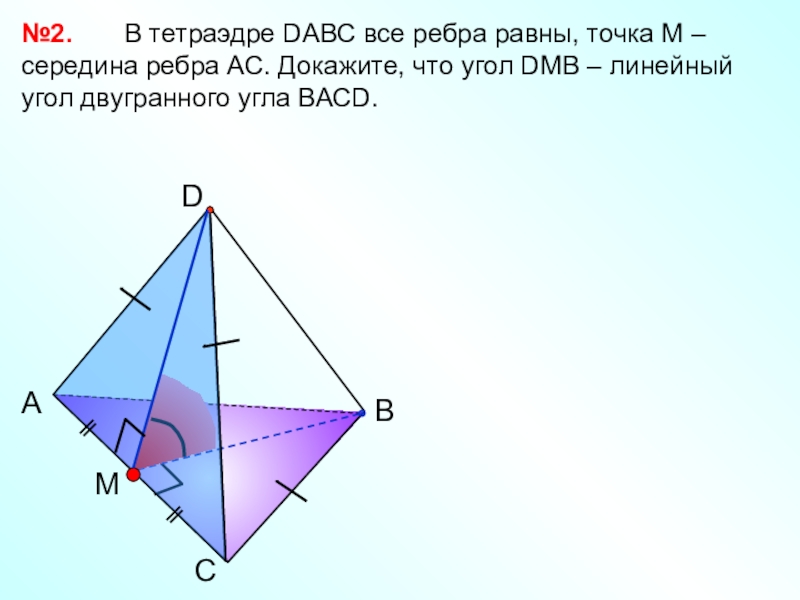
В тетраэдре DАВС
все ребра равны, точка М – середина ребра АС. Докажите,
что угол DМВ – линейный угол двугранного угла ВАСD.№2.
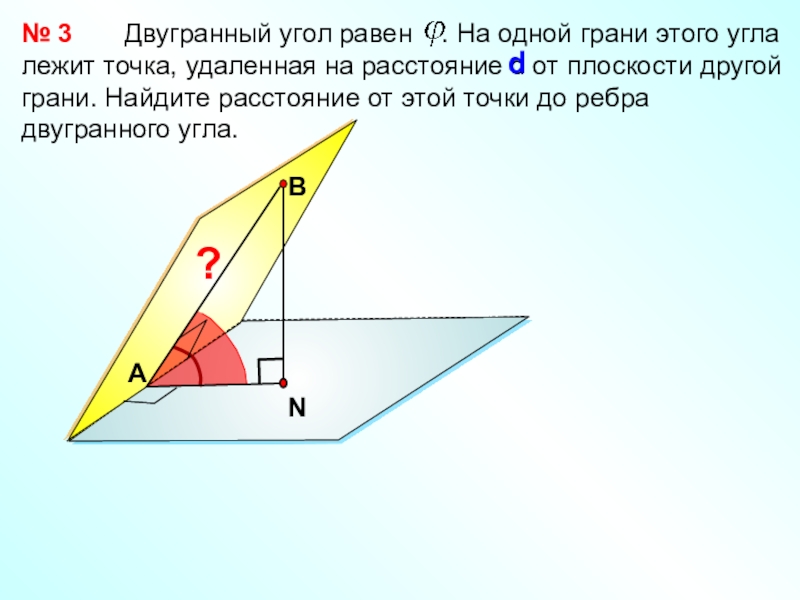
Слайд 30 Двугранный угол равен
. На одной грани этого угла лежит точка, удаленная
на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла.№ 3
В
d
А
?
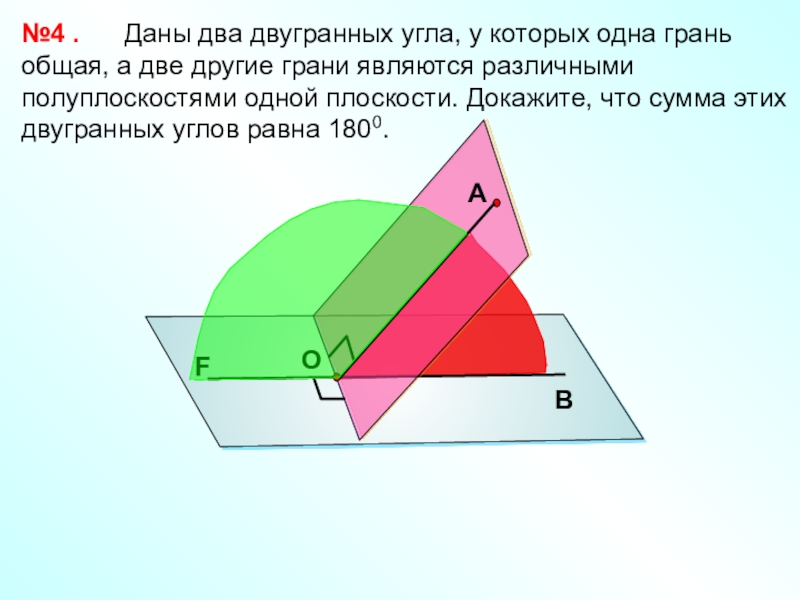
Слайд 31 Даны два двугранных
угла, у которых одна грань общая, а две другие грани
являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 1800.№4 .
А
