Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Экспертные системы в медицине. Моделирование в медицине
Содержание
- 1. Экспертные системы в медицине. Моделирование в медицине
- 2. Интеллектуальные системы поддержки принятия врачебных решений:выполняют задачи
- 3. Экспертные системы (ЭС) как пример интеллектуализации программных
- 4. Структура экспертной системыИнтерфейс пользователяРешательБаза знанийБлок объясненийИнтеллектуаль-ный редактор базы знанийИнженер по знаниям и ЭкспертПользователь (база данных)
- 5. Этапы построения экспертных систем1. Идентификация (определение людских
- 6. Классификация экспертных системЭкспертные системыПо задачеПо связи с реальным временемПо типу ЭВМПо степени интеграции
- 7. Классификация ЭС по задачеПо задачеИнтерпретация данных (обнаружение
- 8. Классификация ЭС по задачеПо задачеПрогнозирование (предсказание погоды
- 9. Классификация ЭС по связи с реальным временемПо связи с реальным временемСтатические КвазидинамическиеДинамические
- 10. Классификация ЭС по типу ЭВМПо типу ЭВМНа
- 11. Классификация ЭС по степени интеграцииПо степени интеграцииАвтономныеГибридные (интегрированные)
- 12. Медицинские экспертные системы MYCIN – промышленная ЭС
- 13. Фрагмент диалога пользователя с MYCIN
- 14. Продолжение диалога пользователя с MYCIN
- 15. Основные понятия моделирования Моделирование – это метод
- 16. Построение моделей включает этапы:1. получение знаний об
- 17. Классификация моделей по области использованияУчебные модели используются
- 18. Классификация моделей по отрасли знанийБиологическиеМедицинские, Химические, Физические и т.д.
- 19. Типы моделей в зависимости от целей использованияОптимизационные
- 20. Классификация моделей по способу представленияПредметные модели -
- 21. Классификация информационных моделей в зависимости от временного
- 22. Типы моделей в медицинеВещественные – имеют внешнее
- 23. Типы математических моделей в медицинеДетерминированные – формула
- 24. Цели математического моделирования в медицинеАдекватно в короткий
- 25. Модель гемодинамики Схематическое изображение кровотока
- 26. Этапы составления математической модели гемодинамикиСкорость изменения объема
- 27. Применяя закон Пуазейля для стационарного течения крови
- 28. Закон изменения давления в крупных сосудах с
- 29. Преимущества использования моделей в медицине 1. с помощью
- 30. Требования к математическому моделированию в медицинеНеобходимость отражения
- 31. Имитационное моделирование в медицинеИмитационное моделирование — это
- 32. Молекулярное моделирование Молекулярное моделирование – это область
- 33. Примеры моделей Расчётные сетки, поля скоростей и
- 34. Расчёт давления в глазу человека при проведении лазерной операции по разрушению хрусталика и расчётная сетка
- 35. Динамика залечивания кожной раны: трёхмерные картины распределения плотности коллагена в начальный и конечный моменты лечения
- 36. Моделирование максимальных сжимающих и растягивающих напряжений при
- 37. Фармакокинетические модели расчет индивидуальных режимов дозирования лекарственных
- 38. Математическая модель внутримышечного введения лекарственного вещества При
- 39. 40 лет 55 лет60 лет 65
- 40. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Интеллектуальные системы поддержки принятия врачебных решений:
выполняют задачи анализа, моделирования и
Слайд 3Экспертные системы (ЭС) как пример интеллектуализации программных средств:
ЭС –
это комплекс программ, аккумулирующий знания специалистов в конкретной предметной области,
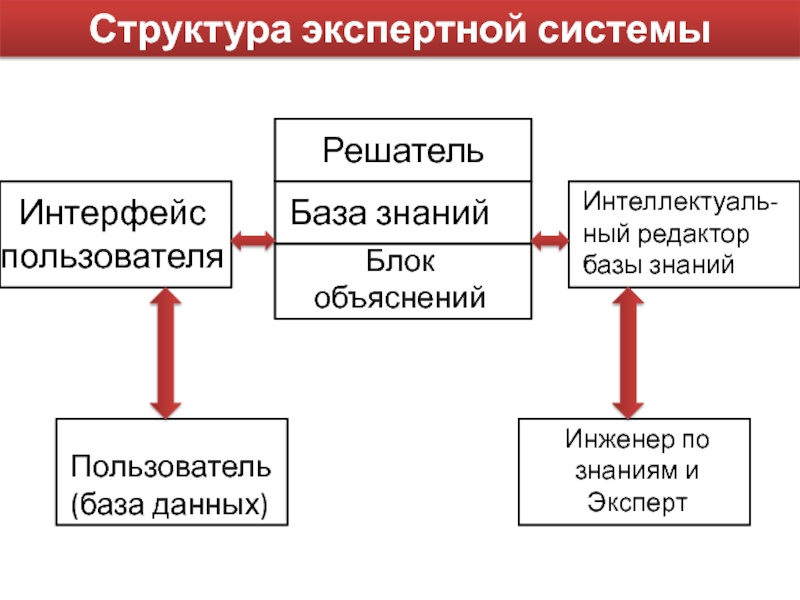
предназначенный для тиражирования знаний и консультаций менее квалифицированных пользователей.Слайд 4Структура экспертной системы
Интерфейс пользователя
Решатель
База знаний
Блок объяснений
Интеллектуаль-ный редактор базы знаний
Инженер по
знаниям и Эксперт
Пользователь (база данных)
Слайд 5Этапы построения экспертных систем
1. Идентификация (определение людских и материальных ресурсов,
класса задач, целей и т.д.);
2. Концептуализация (определяются основные понятия, терминология,
стратегия принятия решений и т.д.);3. Формализация (выбор языка представления знаний, продукционные модели, семантические сети и т.д.);
4. Разработка прототипа (создание усеченной версии для проверки работы программы);
5. Тестирование (выявление ошибок, адекватности интерфейса и т.д.);
6. Опытная эксплуатация.
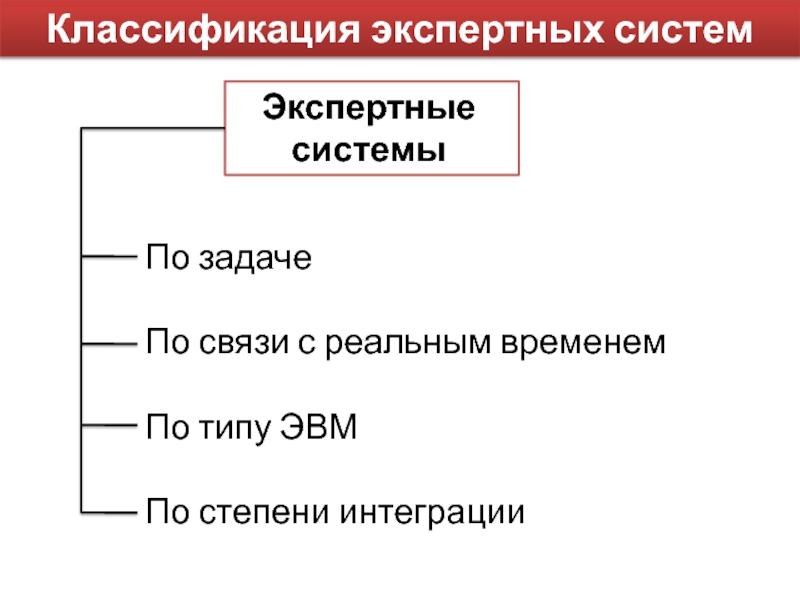
Слайд 6Классификация экспертных систем
Экспертные системы
По задаче
По связи с реальным временем
По типу
ЭВМ
По степени интеграции
Слайд 7Классификация ЭС по задаче
По задаче
Интерпретация данных (обнаружение и идентификация различных
типов океанских судов – SIAP, определение свойств личности – АВТАНТЕСТ
и др.)Диагностика (медицинская, аппаратуры, математического обеспечение и др.)
Мониторинг (помощь диспетчерам атомного реактора – REACTOR, контроль за работой электростанций, аварийных датчиков)
Проектирование (конфигураций ЭВМ, синтез электрических цепей – SYN и др.)
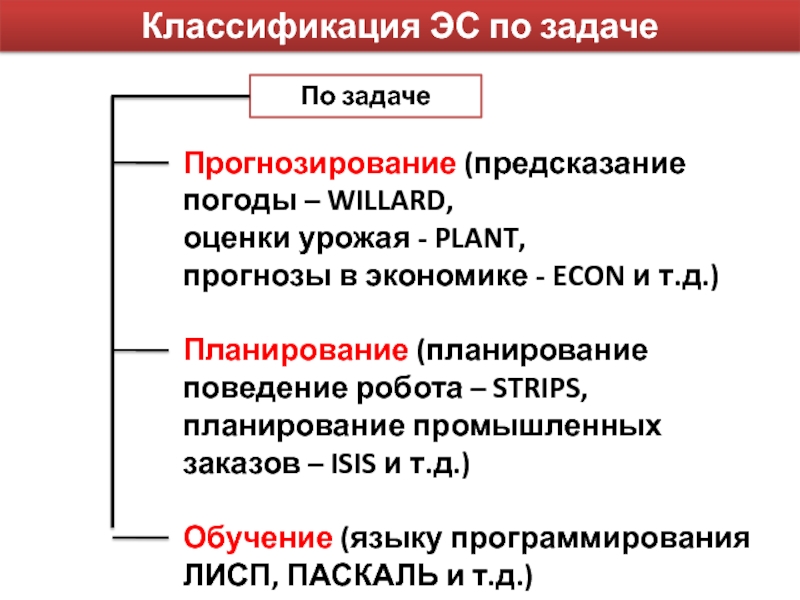
Слайд 8Классификация ЭС по задаче
По задаче
Прогнозирование (предсказание погоды – WILLARD,
оценки
урожая - PLANT,
прогнозы в экономике - ECON и т.д.)
Планирование
(планирование поведение робота – STRIPS, планирование промышленных заказов – ISIS и т.д.)Обучение (языку программирования ЛИСП, ПАСКАЛЬ и т.д.)
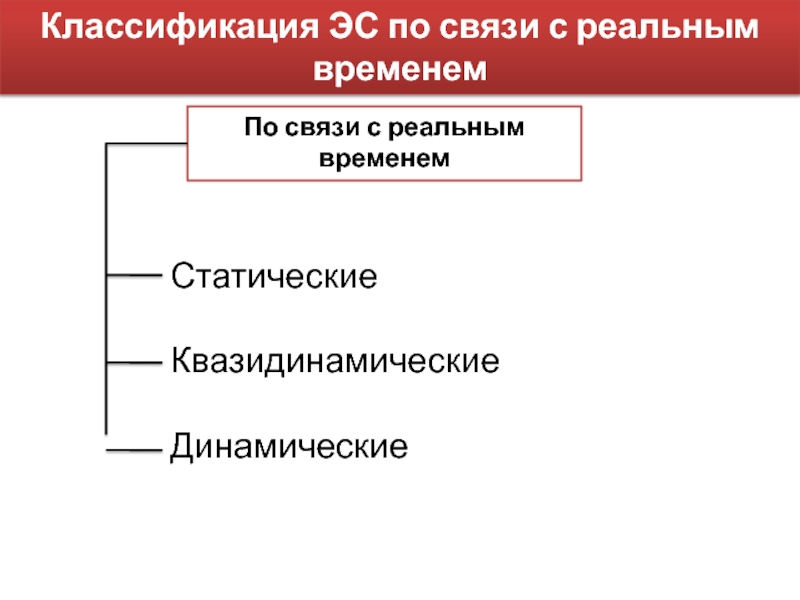
Слайд 9Классификация ЭС по связи с реальным временем
По связи с реальным
временем
Статические
Квазидинамические
Динамические
Слайд 10Классификация ЭС по типу ЭВМ
По типу ЭВМ
На суперЭВМ
На ЭВМ средней
производительности
На символьных процессорах
На мини- и супермини- ЭВМ
На ПЭВМ
Слайд 11Классификация ЭС по степени интеграции
По степени интеграции
Автономные
Гибридные (интегрированные)
Слайд 12Медицинские экспертные системы
MYCIN – промышленная ЭС для диагностики и
лечения инфекционных заболеваний крови.
EMYCIN – Empty MYCIN (пустой МИЦИН), диагностическая
ЭС с незаполненной базой данных. Возможно использование для диагностики и лечения заболеваний разного профиля.ANGY – диагностика и терапия сужения коронарных сосудов.
ДИАГЕН – диагностика наследственных болезней.
ДИН – диагностика неотложных состояний, используется при стёртой клинической картине заболеваний.
ВЕСТ-СИНДРОМ – диагностика судорожных состояний (эпилепсии).
Другие.
Слайд 15Основные понятия моделирования
Моделирование – это метод познания, состоящий в
создании и исследовании моделей.
Модель – это новый объект, который
отражает существенные особенности изучаемого объекта, явления или процесса.Процесс моделирования включает три элемента: субъект (исследователь), объект исследования, модель, опосредствующую отношения познающего субъекта и познаваемого объекта.
Слайд 16Построение моделей включает этапы:
1. получение знаний об объекте-оригинале
2. проведение экспериментов
с моделью - исследование «поведения» модели
3. перенос знаний с
модели на оригинал 4. практическая проверка получаемых с помощью моделей знаний
и их использование для построения обобщающей теории объекта, его преобразования или управления им.
Слайд 17Классификация моделей по области использования
Учебные модели используются при обучении. Например,
наглядные пособия, различные тренажеры, обучающие программы.
Опытные модели используются для
исследования объекта и прогнозирования его будущих характеристик. Например, искусственные протезы клапанов сердца. Научно-технические модели создаются для исследования процессов и явлений. К таким моделям можно отнести модель движения планет Солнечной системы, модель камер сердца и его клапанов.
Игровые модели — это различного рода игры: деловые, экономические, лечебные. С помощью таких моделей можно разрешать конфликтные ситуации, оказывать психологическую помощь, проигрывать поведение объекта в различных ситуациях.
Имитационные модели имитируют реальность с той или иной степенью точности.
Слайд 18Классификация моделей по отрасли знаний
Биологические
Медицинские,
Химические,
Физические и т.д.
Слайд 19Типы моделей в зависимости от целей использования
Оптимизационные – предназначены для
определения новых свойств моделируемого объекта. Например, расчет вероятности развития осложнения
после операции.Описательные - описывают поведение некоторой системы и не предназначены для целей управления. Например, формулы, описывающие изменение концентрации лекарственного вещества в крови после его введения .
Слайд 20Классификация моделей по способу представления
Предметные модели - воспроизводят геометрические, физические
и другие свойства объектов в материальном мире. Например, искусственный хрусталик,
искусственный тазобедренный сустав, скелет человекаИнформационные модели – отражают свойства объектов, предметов или процессов с помощью ассоциативных знаков (слова, рисунки, схемы, чертежи, формулы и т.д.). Например, схема кровоснабжения сердца.
Типы информационных моделей: словесные, графические, математические.
В зависимости от структуры информационные модели делятся на табличные, иерархические и сетевые.
Слайд 21Классификация информационных моделей в зависимости от временного фактора
Статические –
модель описывает систему в определенный момент времени. Например, классификации заболеваний,
методов исследования.Динамические – описывает процессы изменения и развития систем. Например, схематическое описание развития физиологических систем в процессе развития ребенка
Слайд 22Типы моделей в медицине
Вещественные – имеют внешнее сходством с объектом
моделирования. Например, протез нижней конечности.
Энергетические – моделируют функцию организма при
отсутствии внешнего сходства. Например, искусственная почка.Смешанные – моделируют и внешнее сходство объекта и его функцию. Например, дистанционно управляемый протез.
Информационные – описывают объект с помощью ассоциативных знаков.
Биологические – заболевания модулируют на животных. Например, крысы с эпилепсией, тугоухостью, артериальной гипертензией.
Слайд 23Типы математических моделей в медицине
Детерминированные – формула описывает функциональную связь
между показателями. Например, минутный объем крови – это произведение фракции
выброса крови левым желудочком сердца на частоту сокращений сердца.Вероятностные – результат оценивается с помощью вероятностных характеристик. Например, расчет анестезиологического и операционного риска по возрасту, исходным показателям функционирования систем организма, типа операции.
Слайд 24Цели математического моделирования в медицине
Адекватно в короткий срок обобщить сложную
сущность явлений и процессов в медицине
Описать и понять факты, выявить
взаимосвязи между элементамиНайти рациональное решение с наибольшей полнотой и надежностью.
Быстро и эффективно проверять гипотезы без обращения к эксперименту.
Предсказывать поведение реальной системы.
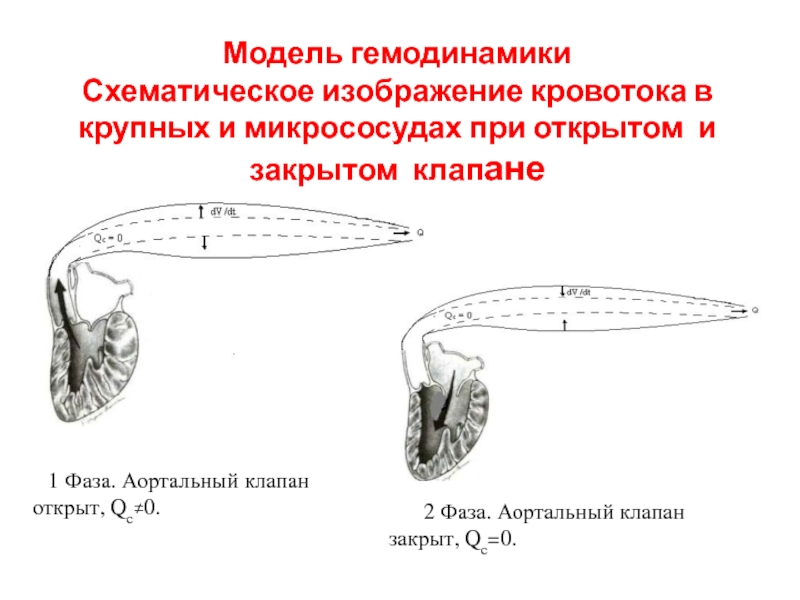
Слайд 25 Модель гемодинамики Схематическое изображение кровотока в крупных и микрососудах при открытом
и закрытом клапане
1 Фаза. Аортальный клапан открыт, Qс≠0.
2 Фаза. Аортальный
клапан закрыт, Qс=0.Слайд 26Этапы составления математической модели гемодинамики
Скорость изменения объема резервуара dV/dt равняется
разности скоростей притока в него крови из сердца Qc и
оттока в систему микрососудов Q:dV=Qc(t) - Q(t) (1)
где Qc(t) - объемная скорость поступления крови из сердца, Q(t) - объемная скорость кровотока в начале мелких сосудов, dV- изменение объема крупных сосудов.
Изменение объема резервуара линейно зависит от изменения давления крови в нем dP:
dV= CdP (2)
где С (эластичность стенок аорты) коэффициент
пропорциональности между давлением и объемом.
С ~ 1/Е, Е- модуль упругости стенок крупных сосудов.
Слайд 27Применяя закон Пуазейля для стационарного течения крови по жесткой трубке
получим, что:
Q(t) = (3)где P(t) - давление в крупных сосудах (в том числе на входе в мелкие), Ркон - давление на выходе из жесткой трубки, Х- гидравлическое сопротивление мелких сосудов. Во всех уравнениях под Р(t) понимается избыточное давление (разность между реальным давлением и атмосферным).
Систему уравнений (1, 2, 3) решаем относительно P(t), Q(t) или V(t). Решим систему относительно P(t).
С учетом 1, 2, 3 получим уравнение :
(4)
Это неоднородное линейное дифференциальное уравнение, решение которого определяется видом функции Qc(t).
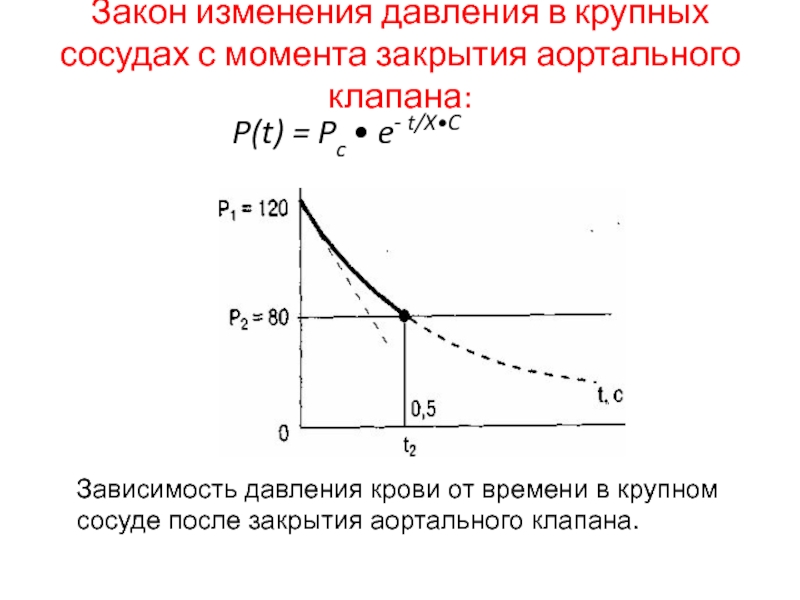
Слайд 28Закон изменения давления в крупных сосудах с момента закрытия аортального
клапана:
P(t) =
Pc • e- t/X•CЗависимость давления крови от времени в крупном сосуде после закрытия аортального клапана.
Слайд 29Преимущества использования моделей в медицине
1. с помощью метода моделиpования на
одном комплексе данных можно pазpаботать целый pяд pазличных моделей, по
pазному интеpпpетиpовать исследуемое явление, и выбpать наиболее плодотвоpную из них для теоpетического истолкования.2. в пpоцессе постpоения модели можно сделать pазличные дополнения к исследуемой гипотезе и получить ее упpощение.
3. в случае сложных математических моделей можно пpименять компьютер и повысить аналитические возможности.
4. откpывается возможность пpоведения модельных экспеpиментов.
Слайд 30Требования к математическому моделированию в медицине
Необходимость отражения патологических процессов и
компенсаторных сдвигов, лечебных воздействий (медикаментозных, изменения режима вентиляции, жидкостного баланса
и пр.),Необходимость представления клинического контроля,
Оценка модели в реальном времени
Наличие интерактивного (диалогового) управления исследовательских процессов в терминах, принятых в клинике.
Слайд 31Имитационное моделирование
в медицине
Имитационное моделирование — это метод исследования, при котором
изучаемая система заменяется моделью, с достаточной точностью описывающей реальную систему
и с ней проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте).Современная технология имитационного моделирования решает задачи в сфере здравоохранения и фармацевтической отрасли. Например, анализ бизнес-процессов при проектировании больниц, оптимизация количества персонала и медицинского оборудования, планирование выхода на рынок новых лекарственных препаратов.
Слайд 32Молекулярное моделирование
Молекулярное моделирование – это область исследований, которая привлекает
теоретические и вычислительные методы для моделирования или имитации поведения молекул,
состоящих от нескольких атомов и до «гигантских» биологических цепочек. Общей чертой методов молекулярного моделирования является атомистический уровень описания молекулярных систем.Слайд 33Примеры моделей
Расчётные сетки, поля скоростей и области возможных
поражений
глаза (отмечены черным цветом) при лазерном разрушении хрусталика
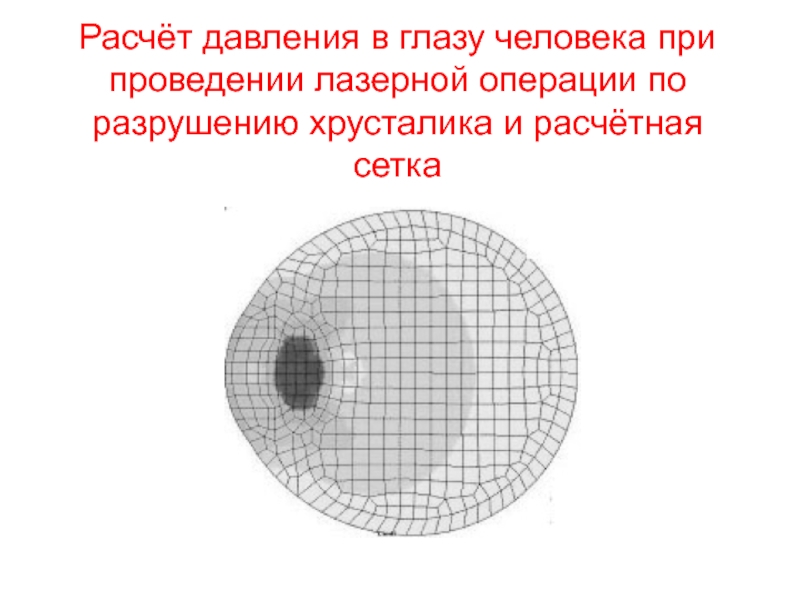
Слайд 34Расчёт давления в глазу человека при проведении лазерной операции по
разрушению хрусталика и расчётная сетка
Слайд 35Динамика залечивания кожной раны: трёхмерные картины распределения плотности коллагена в
начальный и конечный моменты лечения
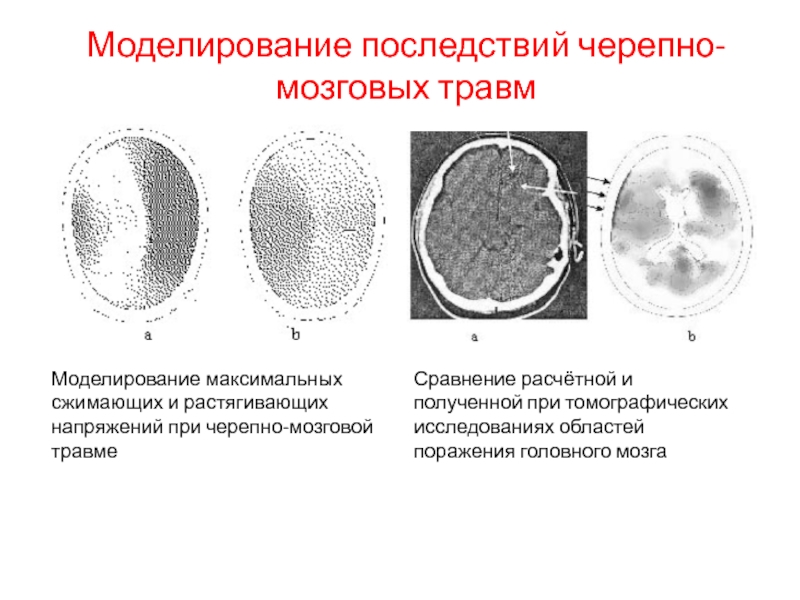
Слайд 36Моделирование максимальных сжимающих и растягивающих напряжений при черепно-мозговой травме
Сравнение расчётной
и полученной при томографических исследованиях областей поражения головного мозга
Моделирование
последствий черепно-мозговых травм Слайд 37Фармакокинетические модели
расчет индивидуальных режимов дозирования лекарственных препаратов с помощью
реализации математических моделей фармакокинетики
подбор индивидуальных режимов дозирования конкретного препарата с
помощью компьютерной модели (подбор скорости длительной инфузии препарата; подбор нагрузочной дозы, кратности введения, поддерживающей дозы при дробном введении препарата)Слайд 38Математическая модель внутримышечного введения лекарственного вещества
При внутримышечном введении лекарственное
вещество сначала попадает в мышцу, а затем диффундирует из мышцы
в кровь, причем скорость этого процесса тем выше, чем больше масса лекарственного вещества в мышце в данный момент времени - m(t) .Применяя закон сохранения массы к количеству лекарственного вещества, содержащегося в мышце, и к количеству лекарственного вещества в кажущемся объеме получим 2 уравнения:
m(t+h) = m(t) - λ*m(t)*h (3)
c(t+h) = c(t) +[λ*m(t) – Cl*c(t)]*h/V (4)
При t=0
m(0) = D, c(0) = Co (5)
где λ – коэффициент скорости диффузии препарата из мышцы в кровь, D – доза препарата.
Слайд 39
40 лет
55 лет
60 лет
65 лет
Систолическое
АД (мм рт. ст.)
180
160
140 120
180
180
160
140
120
140
120
160
120
140
160
180
120
180
140
160
Общий холестерин
10 - 14%
Женщины
Мужчины
50 лет
ммоль/л
мг
/
дл
4
5
6
7
8
4
5
6
7
8
4
5
6
7
8
4
5
6
7
8
150
200
250
300
150
200
250
300
150
200
250
300
150
200
250
300
НЕКУРЯЩИЕ
КУРЯЩИЕ
НЕКУРЯЩИЕ
КУРЯЩИЕ
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
1
3
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
1
3
3
3
2
2
3
3
3
3
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
6
6
6
6
8
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
7
8
9
7
8
9
7
8
9
7
7
8
9
7
7
8
9
9
8
9
7
9
9
9
7
9
7
9
7
8
8
7
8
7
8
6
9
8
9
8
7
7
8
7
8
7
10
10
12
14
11
11
13
12
13
10
12
14
10
12
12
14
10
12
12
10
11
13
10
12
14
13
11
13
11
13
14
10
11
13
11
10
12
13
13
10
12
15
15
15
15
16
16
17
19
22
16
19
22
26
18
26
30
35
41
47
18
21
25
29
34
17
20
24
17
16
19
22
16
18
21
24
28
33
17
20
24
17
15%
6 - 9%
4 - 5%
<1%
1%
2%
3%
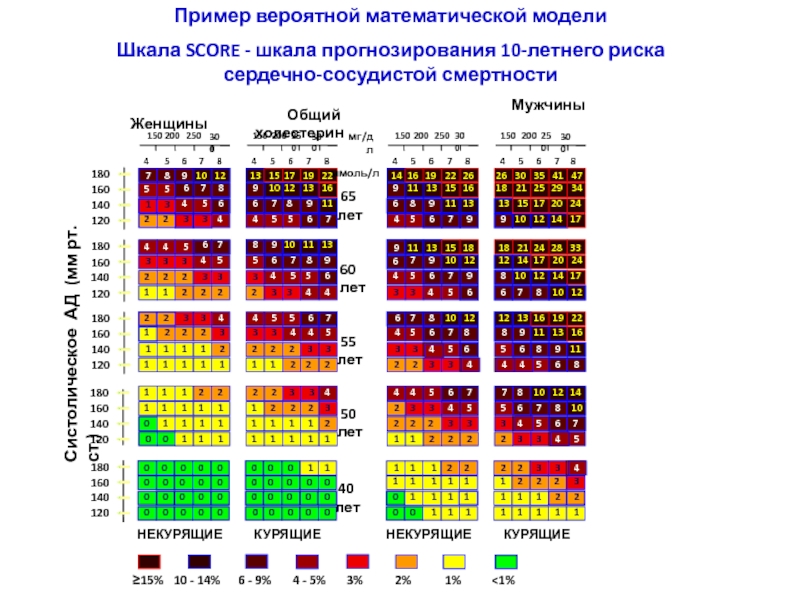
Пример вероятной математической модели
Шкала SCORE - шкала прогнозирования 10-летнего риска сердечно-сосудистой смертности