Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электрические цепи при несинусоидальных воздействиях
Содержание
- 1. Электрические цепи при несинусоидальных воздействиях
- 2. Литература:1. Зевеке Г.В., Ионкин А.В., Страков С.В.
- 3. 1. Основные определения и примеры несинусоидальных колебаний
- 4. При рассмотрении периодических несинусоидальных колебаний обычно пользуются
- 5. Аналитическое выражение несинусоидальной периодической функции (например -
- 6. Несинусоидальные периодические колебания, которые встречаются на практике,
- 7. Периодические колебания симметричные относительно оси абсцисс
- 8. Аппроксимирующее выражение ряда Фурье для колебания типа
- 9. Таким образом, амплитудно-частотный спектр колебания типа «меандр»U0=0Амплитудно-частотный
- 10. Периодические колебания симметричные относительно оси ординат
- 11. Воспользоваться формулой преобразования произведения тригонометрических функций в сумму Аналитическая запись ряда Фурье такого несинусоидального колебания
- 12. «Выпрямленное» гармоническое колебание:Такое несинусоидальное колебание формируется
- 13. Периодическая последовательность прямоугольных импульсов:Формы аналитической запись
- 14. Коэффициенты разложения ряда ФурьеПри этом амплитуды гармоник
- 15. Вид спектра импульсной последовательности существенно зависит от
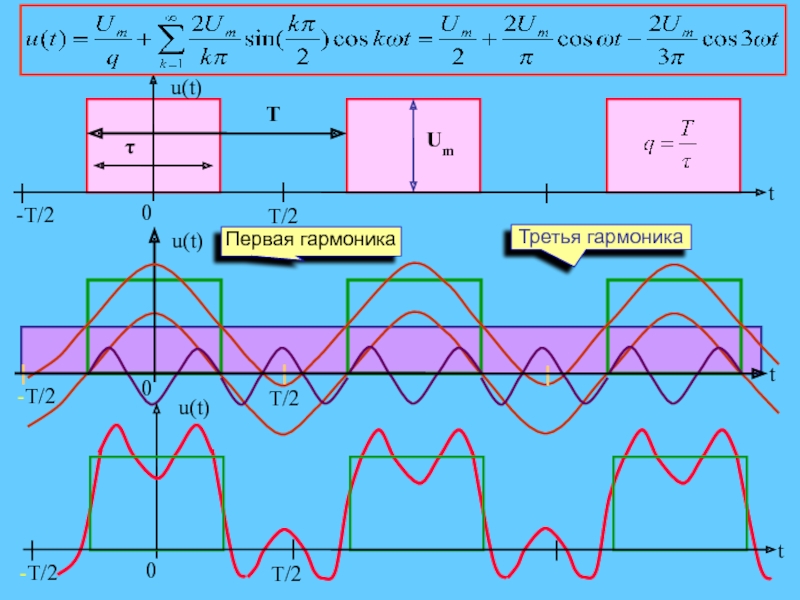
- 16. T/2-T/2u(t)Первая гармоникаТретья гармоника
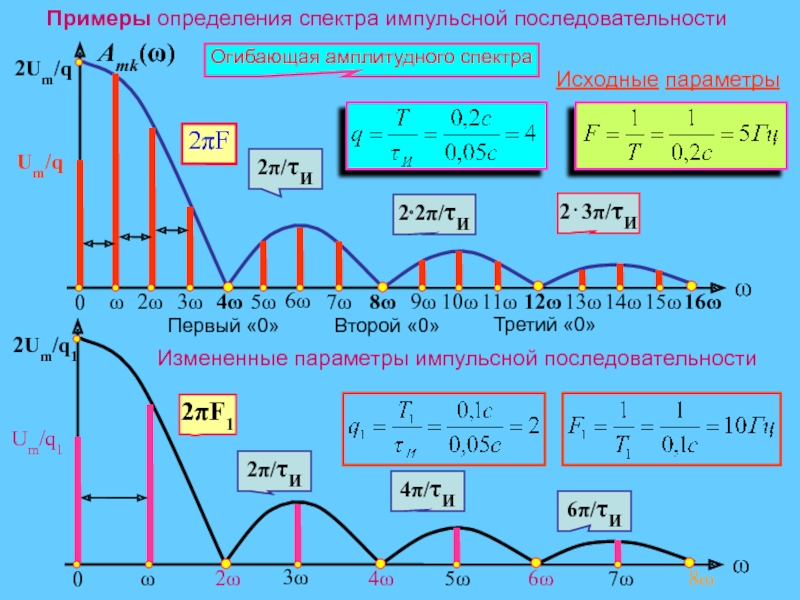
- 17. Примеры определения спектра импульсной последовательности
- 18. Слайд 18
- 19. Слайд 19
- 20. Особенности спектрального состава импульсной последовательности Ширина
- 21. 3. Определение действующих значений несинусоидальных энергетических величинОпределение:
- 22. Для оценки несинусоидальности периодических величин (тока, напряжения,
- 23. Мощность в электрических цепях несинусоидального
- 24. Требуется записать мгновенное значение тока i(t) в
- 25. 3. Полные (модули) сопротивления цепи для первой
- 26. 7. Вольтметр V1, подключенный ко входу цепи
- 27. 9. На участке АВ падение напряжения для
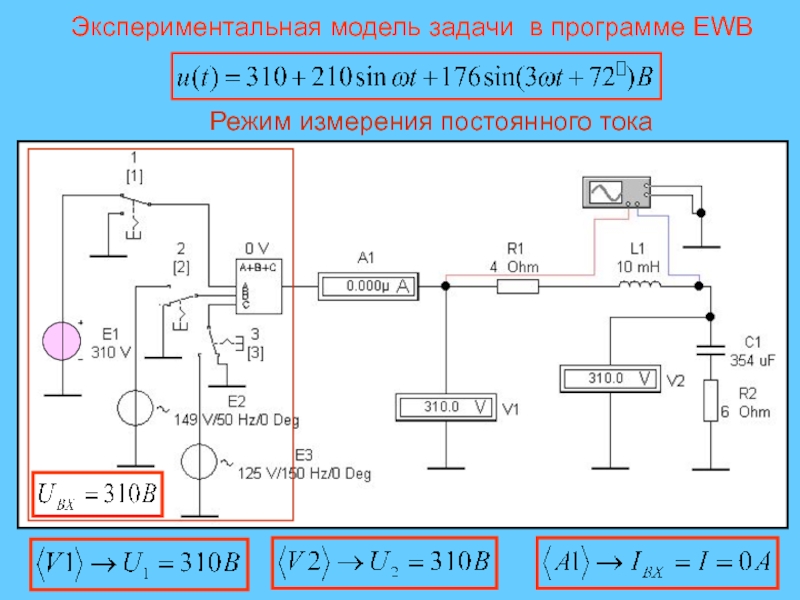
- 28. Экспериментальная модель задачи в программе EWBРежим измерения постоянного тока
- 29. Режим измерения переменного токаИзмерительные приборы показывают действующие значения I и U 1-й гармоники
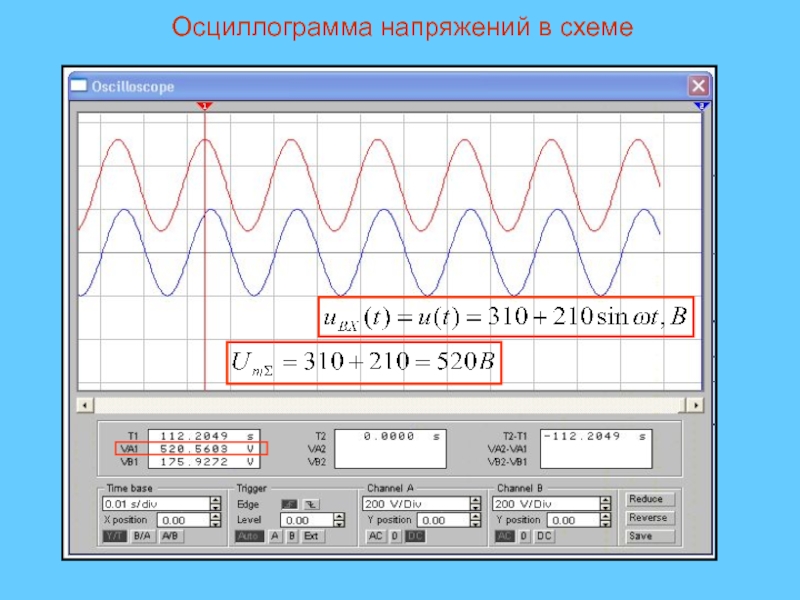
- 30. Осциллограмма напряжений в схеме
- 31. Режим измерения переменного токаПриборы показывают действующие значения I и U 1-й и 3-й гармоник
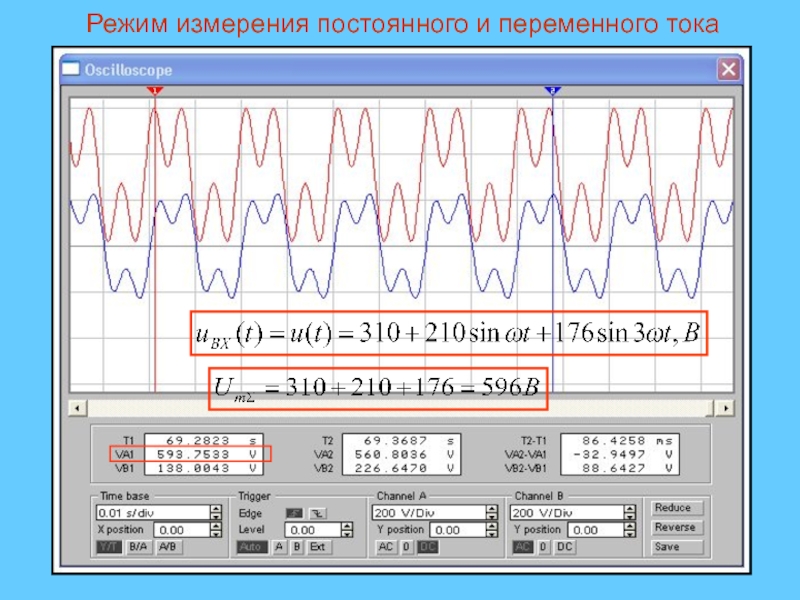
- 32. Режим измерения постоянного и переменного тока
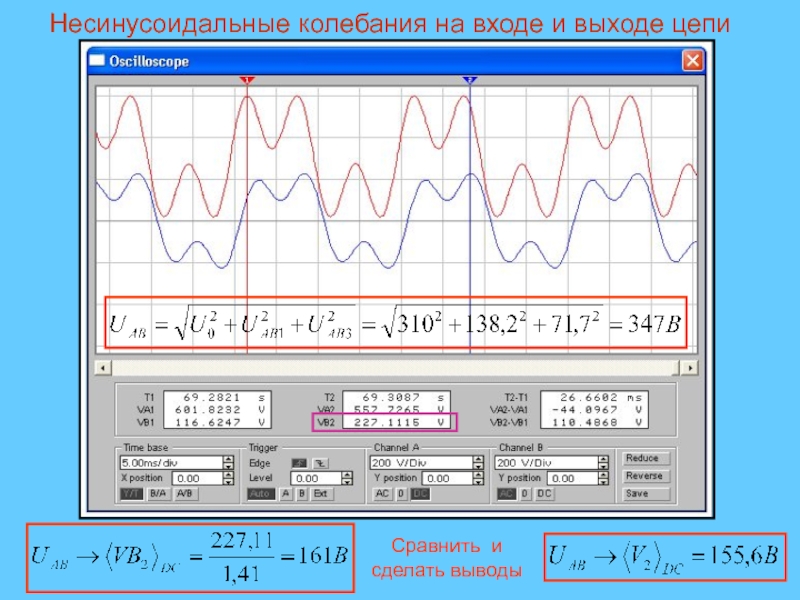
- 33. Несинусоидальные колебания на входе и выходе цепиСравнить и сделать выводы
- 34. Задание на самостоятельную работуЛитература:1. Зевеке Г.В., Ионкин
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 Кубанский государственный технологический университет
Кафедра компьютерных технологий и информационной безопасности
Институт
информационных технологий и безопасности
и расчет электрических цепей при несинусоидальных воздействияхСлайд 2Литература:
1. Зевеке Г.В., Ионкин А.В., Страков С.В. Основы теории цепей:
Учебник для вузов, - М.: Энергоатомиздат, 2004 г, с. 19
– 71.2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 7 –79.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.: Высшая школа, 2003 г, с. 22 – 81.
Учебные вопросы:
1. Основные определения и примеры несинусоидальных колебаний в электрических цепях
3. Определение действующих значений несинусоидальных энергетических величин
2. Временной и спектральный анализ несинусоидальных колебаний в цепях переменного тока
Слайд 31. Основные определения и примеры несинусоидальных колебаний в электрических цепях
Периодическими
несинусоидальными колебаниями называются токи (напряжения), изменяющиеся по времени по периодическому
несинусоидальному законуРежимы работы электрических цепей при которых возникают несинусоидальные токи или напряжения
4 режима работы
1.
Источник электрической энергии вырабатывает несинусоидальную ЭДС или ток, а все элементы ЭЦ являются линейными (линейные ЭЦ)
2.
Источник электрической энергии вырабатывает синусоидальную ЭДС или ток, но хотя бы один из элементов ЭЦ является нелинейным (нелинейные ЭЦ – катушка со стальным сердечником, выпрямители)
3.
Источник электрической энергии вырабатывает несинусоидальную ЭДС или ток, а в ЭЦ входят нелинейные сопротивления (НЭЦ)
4.
Источник электрической энергии вырабатывает постоянную или синусоидальную ЭДС или ток, а один или несколько элементов ЭЦ изменяют свои параметры в процессе работы (параметрические ЭЦ)
Причина несинусоидальности
Источник энергии
Нагрузка ЭЦ
Слайд 4При рассмотрении периодических несинусоидальных колебаний обычно пользуются математическим аппаратом -
рядом Фурье.
Любая периодически изменяющаяся величина может быть представлена в виде
суммы постоянной составляющей и ряда синусоидальных составляющих с кратными частотамиПостоянная составляющая
Амплитуда k – й гармоники
Угловая частота k – й гармоники
Гармоника - синусоидальная составляющая несинусоидального колебания
Угловая частота первой (основной) гармоники
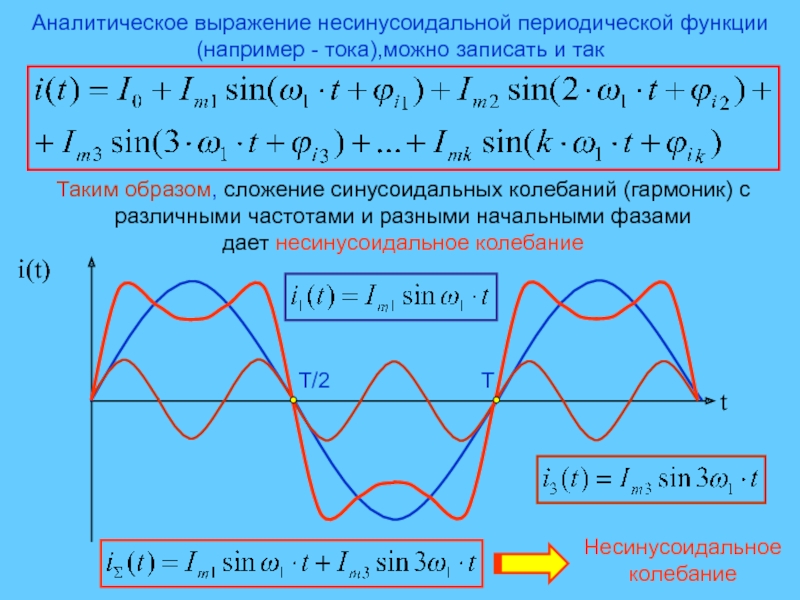
Слайд 5Аналитическое выражение несинусоидальной периодической функции (например - тока),можно записать и
так
Таким образом, сложение синусоидальных колебаний (гармоник) с различными частотами и
разными начальными фазами дает несинусоидальное колебаниеНесинусоидальное колебание
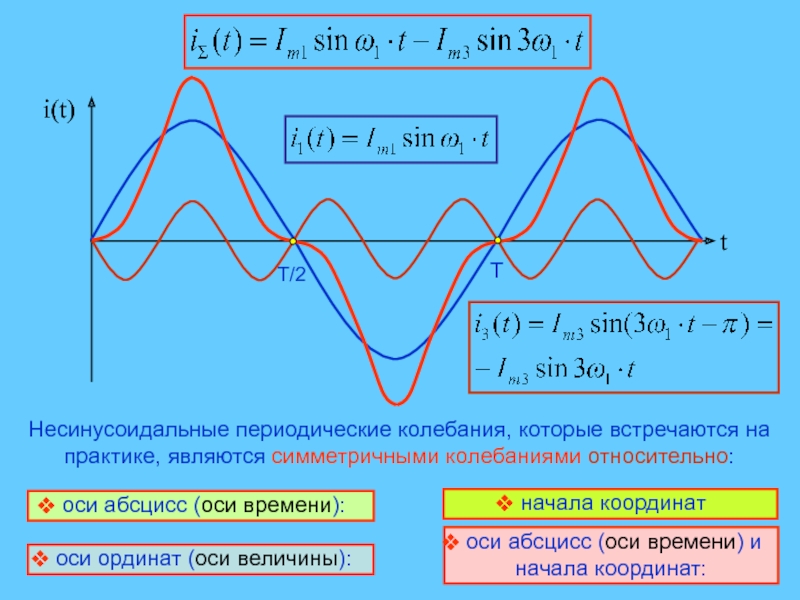
Слайд 6Несинусоидальные периодические колебания, которые встречаются на практике, являются симметричными колебаниями
относительно:
оси абсцисс (оси времени):
оси ординат (оси величины):
начала
координат оси абсцисс (оси времени) и начала координат:
Слайд 7 Периодические колебания симметричные относительно оси абсцисс (оси времени) и
начала координат:
Колебание типа «меандр»
Постоянная составляющая колебания равна «0»
При аппроксимации
u(t) системой ортогональных функции {sinkt} =sint,sin2t,sin3t,…Колебание типа «меандр» при разложении в ряд Фурье содержит только четные sin гармоники
Слайд 8Аппроксимирующее выражение ряда Фурье для колебания типа «меандр»
Обобщенное выражение
ряда Фурье для колебания типа «меандр»
где амплитуды гармоник
расчетные
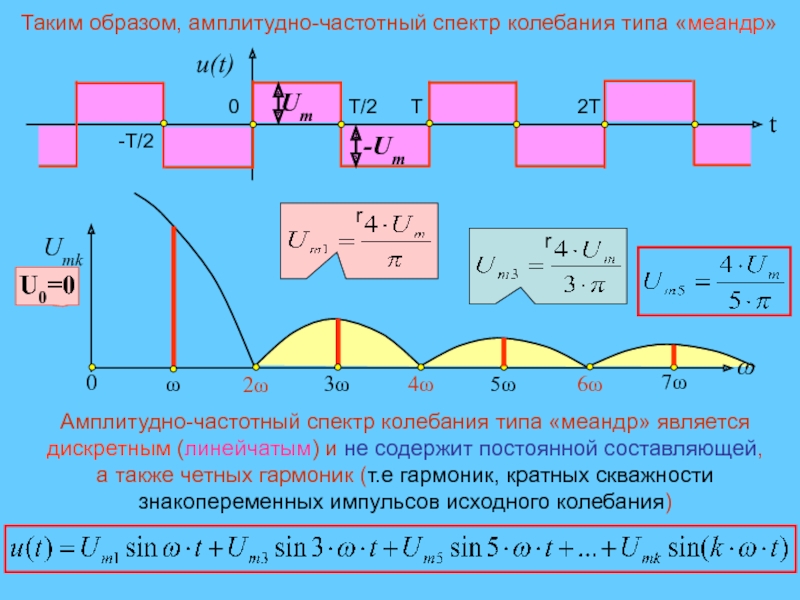
выражения для вычисления коэффициентов ряда ФурьеСлайд 9Таким образом, амплитудно-частотный спектр колебания типа «меандр»
U0=0
Амплитудно-частотный спектр колебания типа
«меандр» является дискретным (линейчатым) и не содержит постоянной составляющей, а
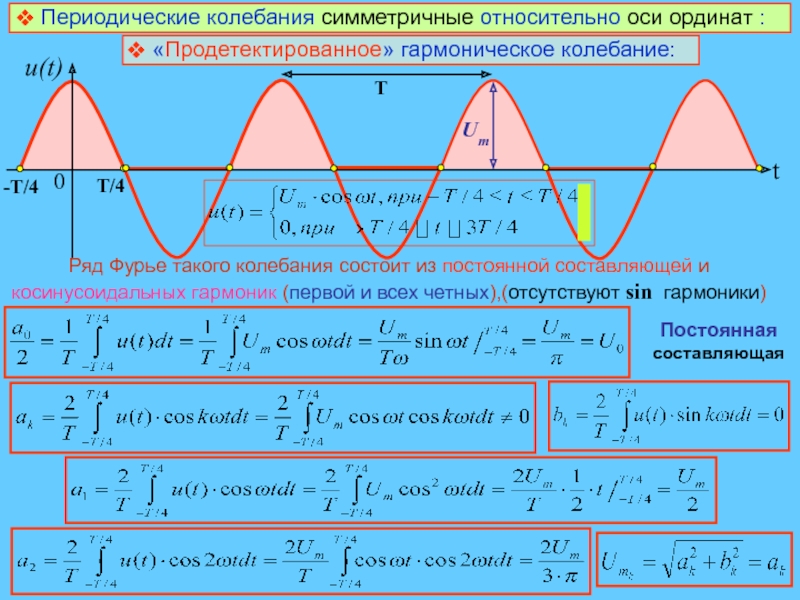
также четных гармоник (т.е гармоник, кратных скважности знакопеременных импульсов исходного колебания)Слайд 10 Периодические колебания симметричные относительно оси ординат :
«Продетектированное» гармоническое
колебание:
Ряд Фурье такого колебания состоит из постоянной составляющей и косинусоидальных
гармоник (первой и всех четных),(отсутствуют sin гармоники)Постоянная составляющая
Слайд 11Воспользоваться формулой преобразования произведения тригонометрических функций в сумму
Аналитическая запись
ряда Фурье такого несинусоидального колебания
Слайд 12 «Выпрямленное» гармоническое колебание:
Такое несинусоидальное колебание формируется на выходе двухполупериодного
однофазного выпрямителя (мостового выпрямителя)
Аналитическая запись ряда Фурье такого несинусоидального колебания
(отсутствует нечетные гармоникиАмплитуды остальных слагаемых удваиваются по сравнению с «продетектированным» колебанием)
Слайд 13 Периодическая последовательность прямоугольных импульсов:
Формы аналитической запись такого несинусоидального колебания
Основные
параметры импульсной последовательности
Период следования импульсов - Т
Длительность импульсов – t И Скважность импульсной последовательности – q
Постоянная составляющая периодической импульсной последовательности
Слайд 14Коэффициенты разложения ряда Фурье
При этом амплитуды гармоник ряда Фурье и
их фазы выражаются как:
Таким образом, на интервале от –Т/2 до
T/2 ряд Фурье выражаетсяСлайд 15
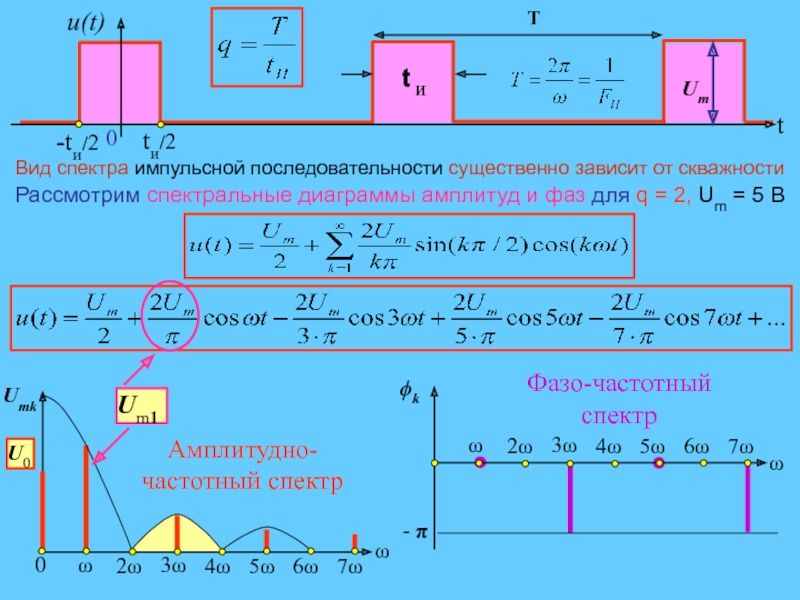
Вид спектра импульсной последовательности существенно зависит от скважности
Рассмотрим спектральные диаграммы
амплитуд и фаз для q = 2, Um = 5
BU0
Амплитудно-частотный спектр
Фазо-частотный спектр
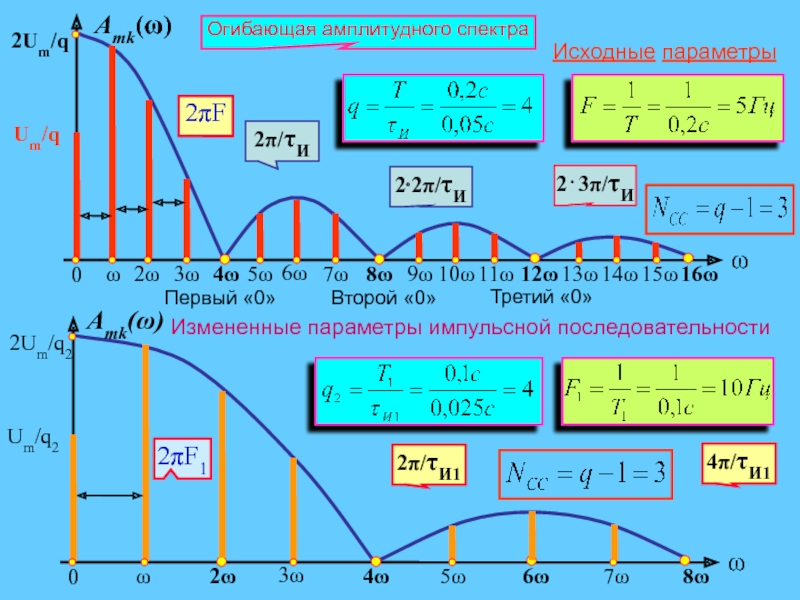
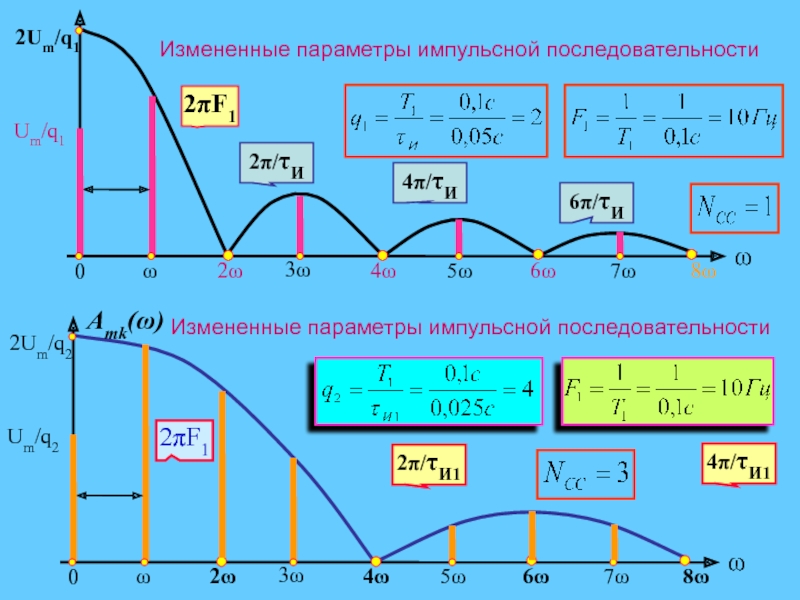
Слайд 20Особенности спектрального состава импульсной последовательности
Ширина каждого лепестка равна
(2π⁄τИ) и определяется только длительностью импульса. Расстояние между спектральными линиями
равно 2πF, F = 1/Т – частота повторения импульсов, т.е. определяется периодом импульсной последовательности. Узлы (нули) амплитудного спектра – значения частот k·ω, в которых Amk(ω) = 0 и происходит смена знака сомножителей спектра, т.е. фаза скачком изменяется на 180°.
Вывод: Амплитудно-частотный спектр периодической последовательности прямоугольных импульсов является дискретным и полностью определяется параметрами импульсной последовательности.
Слайд 213. Определение действующих значений несинусоидальных энергетических величин
Определение: Действующим называют значение
несинусоидального тока, эквивалентное постоянному току по тепловому воздействию
или
Действующее значение
несинусоидального тока является средней квадратичной величиной постоянной составляющей и действующих (или амплитудных) значений токов гармоникили
Действующее значение несинусоидального напряжения является средней квадратичной величиной постоянной составляющей и действующих (или амплитудных) значений напряжений гармоник
Действующие значения несинусоидальных токов и напряжений измеряются амперметрами и вольтметрами электромагнитной, электродинамической и тепловой систем
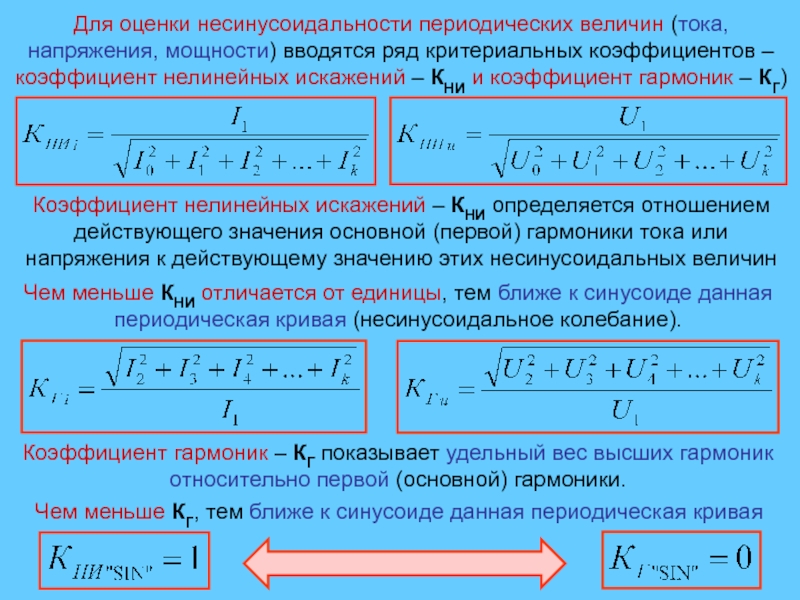
Слайд 22Для оценки несинусоидальности периодических величин (тока, напряжения, мощности) вводятся ряд
критериальных коэффициентов – коэффициент нелинейных искажений – КНИ и коэффициент
гармоник – КГ)Коэффициент нелинейных искажений – КНИ определяется отношением действующего значения основной (первой) гармоники тока или напряжения к действующему значению этих несинусоидальных величин
Чем меньше КНИ отличается от единицы, тем ближе к синусоиде данная периодическая кривая (несинусоидальное колебание).
Коэффициент гармоник – КГ показывает удельный вес высших гармоник относительно первой (основной) гармоники.
Чем меньше КГ, тем ближе к синусоиде данная периодическая кривая
Слайд 23 Мощность в электрических цепях несинусоидального тока
Под активной мощностью
Р несинусоидального тока понимают среднее значение мгновенной мощности за период
Выполнив
интегрирование, получимПотребляемая, т.е. активная мощность в цепи несинусоидального тока определяется суммой постоянной мощности и активных мощностей гармоник
Реактивная мощность в цепи несинусоидального тока определяется суммой реактивных мощностей гармоник
При изучении некоторых свойств цепей несинусоидального тока несинусоидальные токи и напряжения заменяют синусоидальными по критерию эквивалентности действующих значений тока и напряжения.
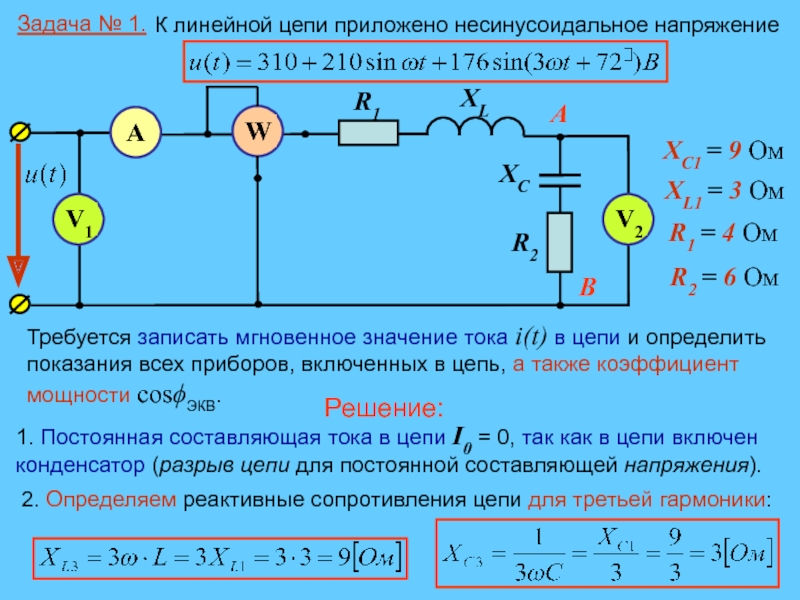
Слайд 24Требуется записать мгновенное значение тока i(t) в цепи и определить
показания всех приборов, включенных в цепь, а также коэффициент мощности
cosϕЭКВ.Решение:
1. Постоянная составляющая тока в цепи I0 = 0, так как в цепи включен конденсатор (разрыв цепи для постоянной составляющей напряжения).
2. Определяем реактивные сопротивления цепи для третьей гармоники:
Слайд 253. Полные (модули) сопротивления цепи для первой и третьей гармоник:
4.
Амплитуды токов первой и третьей гармоник:
5. Углы сдвига фаз для
первой и третьей гармоник тока:6. Мгновенное значение несинусоидального тока в цепи будет иметь вид:
Слайд 267. Вольтметр V1, подключенный ко входу цепи будет показывать действующее
значение приложенного к цепи входного напряжения
так как действующее значение напряжений
первой и третьей гармоник:8. Амперметр A, подключенный на входе цепи будет показывать действующее значение протекающего в цепи тока
так как действующее значение токов первой и третьей гармоник:
9. Для определения показаний второго вольтметра V2, необходимо вычислить полные сопротивления участка АВ для 1-й и 3-й гармоник
Слайд 279. На участке АВ падение напряжения для 1-й и 3-й
гармоник составит
10. Так как постоянная составляющая входного напряжения приложена к
конденсатору, то следовательно, действующее значение напряжения на участке АВ цепи будет равно:11. Ваттметр W измеряет активную мощность цепи,
Следовательно,
12. Для определения эквивалентного коэффициента мощности цепи необходимо вычислить полную мощность цепи,
13. Тогда эквивалентный коэффициент мощности цепи
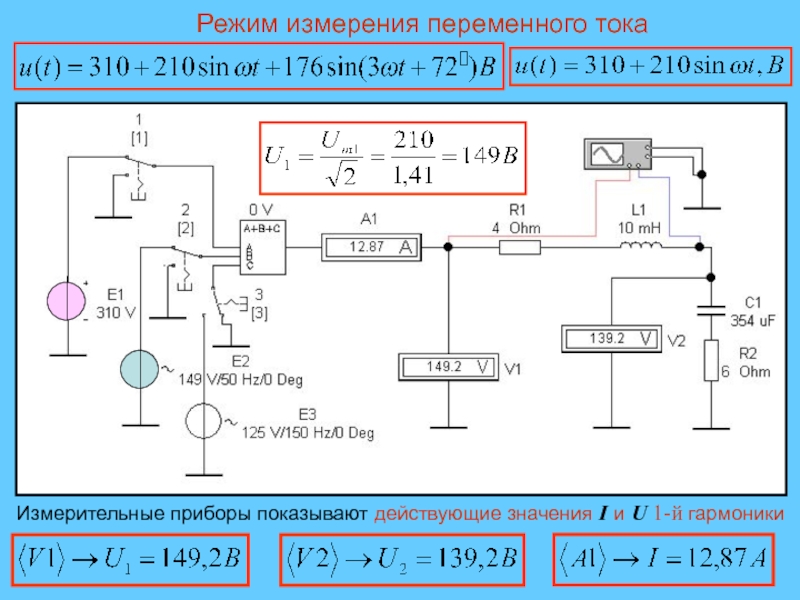
Слайд 29Режим измерения переменного тока
Измерительные приборы показывают действующие значения I и
U 1-й гармоники
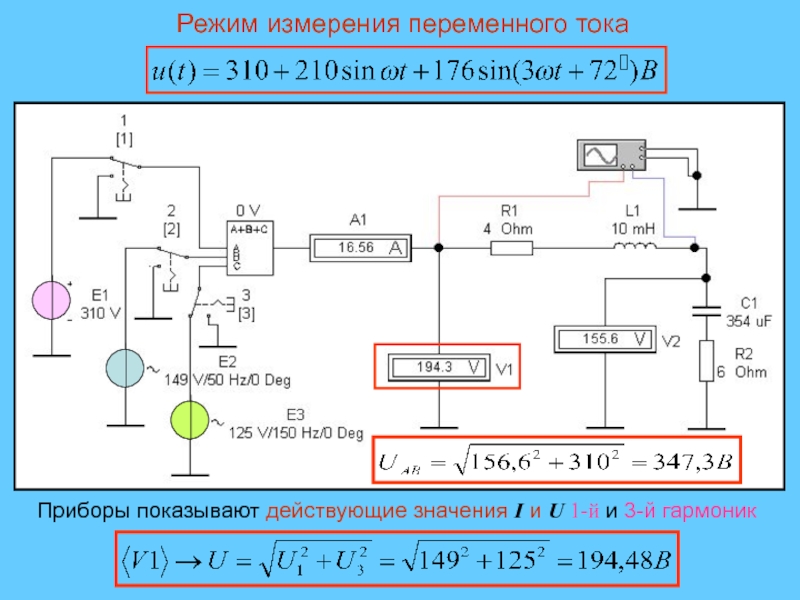
Слайд 31Режим измерения переменного тока
Приборы показывают действующие значения I и U
1-й и 3-й гармоник
Слайд 34Задание на самостоятельную работу
Литература:
1. Зевеке Г.В., Ионкин А.В., Страков С.В.
Основы теории цепей: Учебник для вузов, - М.: Энергоатомиздат, 2004
г, с. 19 – 71.2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 7 –79.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.: Высшая школа, 2003 г, с. 22 – 81.
Изучить и освоить методы анализа и расчета линейных электрических цепей переменного тока при несинусоидальных воздействиях