ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗЕ

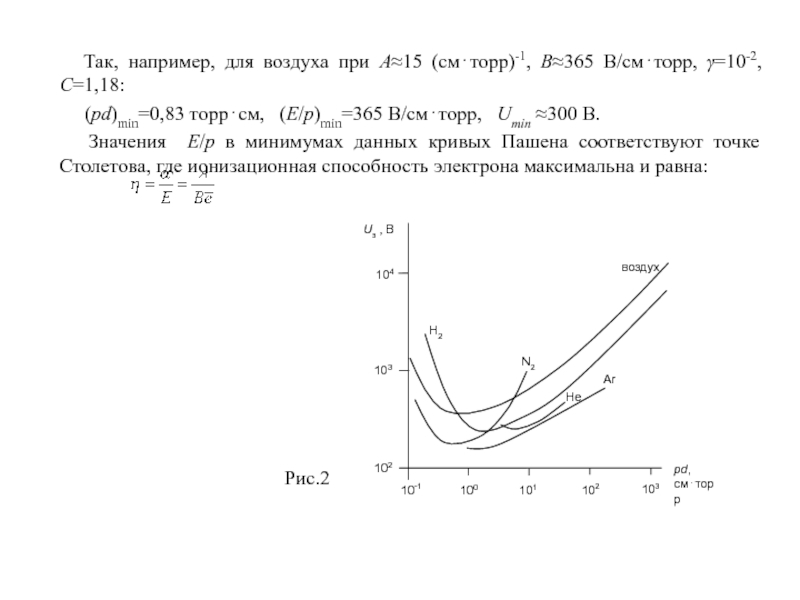
Одной из первых теорий газовых разрядов явилась теория

Таунсенда. Данный вид разряда, названный его именем – таунсендовский имеет очень слабый ток I=10-10-10-5 А и практически не имеет видимого свечения (темновой разряд). При увеличении силы тока до 10-4 А разряд постепенно переходит в тлеющий, который обладает достаточно интенсивным свечением. Наиболее известным применением таунсендовского разряда явился созданный в начале XX века счетчик Гейгера (радиактивных излучений).
Для описания таунсендовского разряда требуется понимание процессов, происходящих в электронных лавинах в газе. Первоначальные наблюдения электронных лавин в газе были выполнены с помощью камеры Вильсона. Для электронной концентрации в лавине можно записать следующие уравнения.


ν (с-1) - частота ионизации – число ионизаций атомов электронами (в среднем) в 1 с.

Для связи длины свободного пробега λi, частоты ионизации νi

и скорости дрейфа uд справедлива следующая формула:


Пространственная зависимость для концентрации в одномерном случае представляется следующим уравнением:


В данное уравнение входит так называемый первый ионизационный коэффициент Таунсенда (см-1) -число ионизаций на расстоянии в 1 см.
Интегрирование уравнения дает следующую экспоненциальную зависимость:

и дрейфовой скоростью электронов с помощью следующего уравнения:

При создании теории Таунсендом (1910 г.) были сделаны следующие исходные предположения относительно характерных особенностей данного разряда:
1) Сила тока считается малой и искажением электрического поля ввиду наличия пространственных зарядов можно пренебречь.
2) Имеют место ионизация газа соударениями электронов и развитие электронных лавин.
3) Разряд может быть несамостоятельным и самостоятельным.
4) Таунсендовский разряд переходит в тлеющий, а затем в дуговой (при увеличении тока).

коэффициенты:
α (см-1) – первый ионизационный коэффициент

Таунсенда, т.е. число электрон-ионных пар, образованных одним электроном на пути в 1 см в направлении от катода к аноду вследствие неупругих столкновений электронов с нейтральными частицами газа;
β (см-1) – аналогичный коэффициент для ионов, т.е. число свободных электронов, образованных положительным ионом на пути в 1 см при движении от анода к катоду;
γ - количество электронов (в среднем) выделяющихся с катода при попадании на него одного иона вследствие ион -электронной эмиссии.
При построении теории предполагалось наличие внешнего ионизатора (источника ультрафиолетового излучения), с помощью которого происходило облучение поверхности катода (рис.1)


Рис.1

(част/см2⋅с) - число электронов, выделяющихся с

1 см2 поверхности катода в 1 с,
(А/см2) - плотность электронного тока с катода.
В простейшем варианте теории ионизация ионами не учитывается, т.е. полагается β<<α.

при x = 0, n = n0 и α = const при E = const
Интегрирование данного уравнения дает экспоненциальную зависимость для концентрации электронов и плотности тока:


Для числа электронов, достигших анода записывается выражение:

вид:


Для рассмотрения стационарного режима разряда все пространство

от катода до анода образно разбивается на участки длиной равной длине ионизации электронами - λi. Предполагается, что имеет место образование электронных лавин на расстоянии равном λi . В стационарном режиме считается, что число электронов в последующей лавине равно числу электронов, участвующих в развитии предыдущей лавины.
Вводятся следующие обозначения:
- общее число электронов, вылетевших с катода в 1 с при стационарном режиме. Выражение для n1 в стационарном режиме разряда может быть записано в виде:

- число образовавшихся ионов
- число выбитых электронов с катода ионами

следующее выражение:

, где

В результате концентрация электронов и плотность тока на аноде записываются в виде:




Предполагается, что эмиссия ионов с поверхности анода под действием электронов пренебрежимо мала. В данной теории изначально предполагалось действие внешнего ионизатора (источника УФ-излучения), создающего вблизи катода исходную концентрацию заряженных частиц n0. В данном случае разряд считается несамостоятельным.

несамостоятельного в самостоятельный требуется выполнение, согласно Таунсенду, условия равенства нулю

знаменателя в формуле для плотности тока:


Эта выражение обычно считается условием зажигания таунсендовского разряда.
В качестве одной из характеристик разряда вводится также величина:
(В-1) - ионизационная способность – число пар ионов, которое в среднем рождает электрон, проходя в однородном поле разность потенциалов в 1 В.
Также можно построить величину, обратную к ионизационной способности:
- количество эВ, которое в среднем затрачивается на образование пары ионов,
(эВ) - константа Столетова, т.е. максимальное значение величины η-1.

газов:
воздух: ≈66

эВ (E/p ≈ 365 В/см⋅торр)
гелий: ≈83 эВ (E/p ≈ 50 В/см⋅торр),
водород: ≈70 эВ (E/p ≈ 140 В/см⋅торр)

Рассмотрим вопрос, связанный с потенциалом зажигания таунсендовского разряда. Для первого коэффициента ионизации Таунсендом была выведена полуэмпирическая формула, учитывающая зависимость данной величины от давления газа и напряжения электрического поля в виде:


Где А и В являются постоянными коэффициентами, определенными для каждого конкретного газа в диапазоне значений E/p. Приведем примеры для значений данных коэффициентов: воздух А≈15 (см⋅торр)-1, В≈365 (В/см⋅торр), при E/p≈100-800 (В/см⋅торр); гелий А≈3 (см⋅торр)-1, В≈34 (В/см⋅торр), при E/p≈20-150 (В/см⋅торр).

стационарности таунсендовского разряда:

В результате потенциал зажигания разряда

выражается в виде:



Экспериментальные кривые для потенциала зажигания таунсендовского разряда впервые были измерены Пашеном. Представим зависимости, полученные для различных газов (рис.2).
Данные кривые хорошо согласуются с формулой, выведенной для Uз. Для значений в минимуме получаются следующие выражения:

В≈365 В/см⋅торр, γ=10-2, С=1,18:
(pd)min=0,83

торр⋅см, (E/p)min=365 В/см⋅торр, Umin ≈300 В.
Значения E/p в минимумах данных кривых Пашена соответствуют точке Столетова, где ионизационная способность электрона максимальна и равна:










Рис.2