Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ СИСТЕМАХ
Содержание
- 1. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ СИСТЕМАХ
- 2. Литература 1. Веников В.А. Переходные электромеханические процессы
- 3. Электромеханические переходные процессыПереходные процессы возникают при переходе
- 4. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ СЛОЖНЫХ СИСТЕМУравнение движения ротора генератора
- 5. Уравнение движения ротора генератораНезначительное возмущение в цепи
- 6. Уравнение движения ротора генератораЗдесь принимается, что при
- 7. Уравнение движения ротора генератораУчитывая, что ускорение представляет
- 8. Уравнение движения ротора генератораТаким образом, при небольших
- 9. Уравнение движения ротора генератораУравнение (12.4) называется уравнением
- 10. Уравнение движения ротора генератораДля учёта влияния активного
- 11. Характеристика мощности при сложной связи генератора с
- 12. Характеристика мощности при сложной связи генератора с
- 13. Характеристика мощности при сложной связи генератора с системой
- 14. Характеристика мощности при сложной связи генератора с
- 15. Характеристика мощности при сложной связи генератора с системой
- 16. Характеристика мощности при сложной связи генератора с
- 17. Характеристика мощности при сложной связи генератора с
- 18. Характеристика мощности при сложной связи генератора с
- 19. Характеристика мощности при сложной связи генератора с системой
- 20. Характеристика мощности при сложной связи генератора с
- 21. Характеристика мощности при сложной связи генератора с системойПереходя к комплексной форме записи комплексных величин, получим
- 22. Характеристика мощности при сложной связи генератора с
- 23. Характеристика мощности при сложной связи генератора с
- 24. Характеристика мощности при сложной связи генератора с
- 25. Характеристика мощности при сложной связи генератора с
- 26. Характеристика мощности при сложной связи генератора с
- 27. Характеристика мощности при сложной связи генератора с
- 28. Статическая устойчивость сложных систем Сложная электрическая система
- 29. Статическая устойчивость сложных системВ отличие от рассмотренных
- 30. Метод малых колебаний Рассмотрим применение метода малых
- 31. Метод малых колебанийПравая часть этого уравнения нелинейна,
- 32. Метод малых колебанийПри малых значениях
- 33. Метод малых колебанийПоскольку
- 34. Метод малых колебанийПодставив (12.8) и (12.9) в
- 35. Метод малых колебанийРешение системы (12.10) можно представить в виде
- 36. Метод малых колебанийРешением этого уравнения является изменение
- 37. Метод малых колебанийПри
- 38. Метод малых колебанийИзменение угла в соответствии с
- 39. Метод малых колебаний
- 40. Анализ статической устойчивости сложных систем методом малых
- 41. Анализ статической устойчивости сложных систем методом малых
- 42. Анализ статической устойчивости сложных систем методом малых
- 43. Анализ статической устойчивости сложных систем методом малых колебаний
- 44. Анализ статической устойчивости сложных систем методом малых
- 45. Анализ статической устойчивости сложных систем методом малых
- 46. Анализ статической устойчивости сложных систем методом малых
- 47. Анализ статической устойчивости сложных систем методом малых
- 48. Анализ статической устойчивости сложных систем методом малых
- 49. Анализ статической устойчивости сложных систем методом малых
- 50. Анализ статической устойчивости сложных систем методом малых
- 51. Анализ статической устойчивости сложных систем методом малых
- 52. Анализ статической устойчивости сложных систем методом малых
- 53. Анализ статической устойчивости сложных систем методом малых
- 54. Критерии устойчивостиВ аналитических расчётах статической устойчивости используется
- 55. Критерии устойчивостиСогласно известным теоремам А.М. Ляпунова, для
- 56. Критерий устойчивости ГурвицаСогласно критерию Гурвица алгебраическое уравнение
- 57. Критерий устойчивости Гурвицат
- 58. В этих определителях элементы, индекс которых превышает
- 59. Критерий устойчивости РауссаПри анализе статической устойчивости системы
- 60. Таблица Раусса
- 61. Критерий устойчивости РауссаДля того чтобы действительная часть
- 62. Критерий устойчивости МихайловаКритерий А.В. Михайлова позволяет выразить
- 63. Критерий устойчивости Михайловапричём
- 64. Критерий устойчивости МихайловаЗадавая значения
- 65. Критерий устойчивости Михайлова
- 66. Критерий устойчивости Михайлова
- 67. Критерий устойчивости МихайловаКритерий Михайлова формулируется следующим образом:
- 68. Метод D – разбиенияМетод D – разбиения
- 69. Метод D – разбиенияМетод D – разбиения
- 70. Метод D – разбиенияЕсли в (12.19) принять
- 71. Метод D – разбиенияТаким образом, D –
- 72. Метод D – разбиенияЕсли параметр ,
- 73. Метод D – разбиенияПеремещаясь из этой области
- 74. Влияние промежуточных подключений на статическую устойчивость генератора При
- 75. Влияние промежуточных подключений на статическую устойчивость генератораЭти
- 76. Влияние промежуточных подключений на статическую устойчивость генератораВзаимные
- 77. Влияние промежуточных подключений на статическую устойчивость генератораВыражения
- 78. Влияние промежуточных подключений на статическую устойчивость генератораКак
- 79. Влияние активного сопротивления на характеристику мощностиПостроим угловые
- 80. Влияние активного сопротивления на характеристику мощностиТогда выражения (12.20) и (12.21) запишем в виде: ;(12.22) .(12.23)
- 81. Влияние активного сопротивления на характеристику мощностиПредел по
- 82. Влияние активного сопротивления на характеристику мощностиРазность
- 83. Влияние активного сопротивления на характеристику мощностиУгловые характеристики мощности Схема замещения простейшей энергосистемы с учётом активногосопротивления
- 84. Влияние активной нагрузкиПоложим, что промежуточная нагрузка Н
- 85. Влияние активной нагрузки
- 86. Влияние активной нагрузки
- 87. Влияние активной нагрузкиДля активно–индуктивной цепи аргументы собственных
- 88. Влияние активной нагрузкиНа рис. 12.7 показаны угловые
- 89. Влияние активной нагрузкиХарактеристики мощности, при наличии поперечного активного сопротивления
- 90. Влияние активной нагрузкиПри подключении активной нагрузки в
- 91. Влияние активной нагрузкиПри подключении активной нагрузки происходит
- 92. Влияние шунтирующего реактораШунтирующие реакторы (ШР) используются в
- 93. Влияние шунтирующего реактораПодключение ШР в промежуточной точке
- 94. Влияние шунтирующего реактора
- 95. Влияние шунтирующего реактораПри пренебрежении активными сопротивлениями элементов
- 96. Влияние шунтирующего реактораПоэтому дополняющие углы
- 97. Влияние шунтирующего реактораПервоначально рассмотрим случай, когда ШР
- 98. Влияние шунтирующего реактораВо втором случае на аналогичные
- 99. Влияние шунтирующего реактораОчевидно, что , а
- 100. Влияние конденсаторной батареиКонденсаторные батареи (КБ) иногда устанавливаются
- 101. Влияние конденсаторной батареи
- 102. Влияние конденсаторной батареиПодключённая КБ в схеме замещения
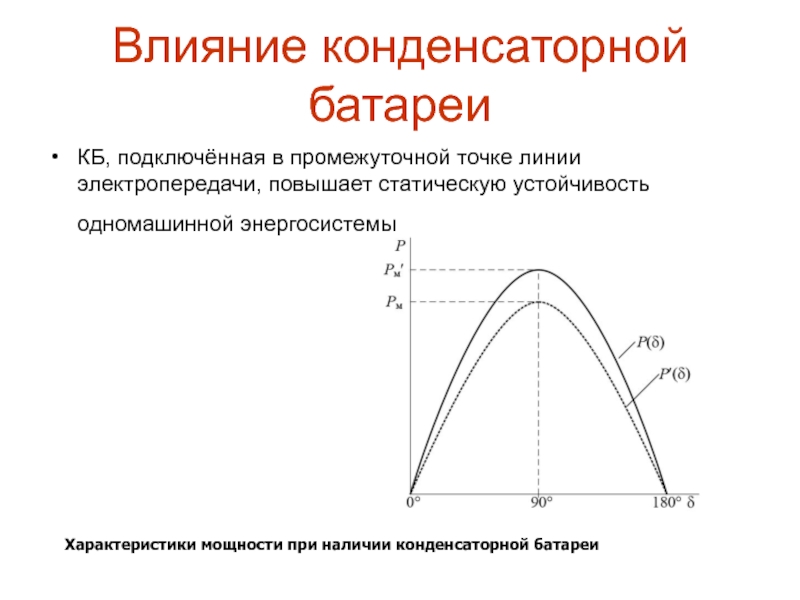
- 103. Влияние конденсаторной батареиКБ, подключённая в промежуточной точке
- 104. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ СИСТЕМАХ
ЧАСТЬ 2
Кафедра Энергетика, автоматика и
системы коммуникаций
Слайд 2Литература
1. Веников В.А. Переходные электромеханические процессы в электрических системах. М.:
Высш. шк., 1985. 536 с.
2. Куликов Ю.А. Переходные процессы в
электрических системах: Учебное пособие. - Новосибирск: Изд-во НГТУ, 2002. – 283 с.3. Устойчивость нагрузки в электрических системах / Ю.И. Гуревич, Л.Е. Лебова, Э.А. Хачатрян. М.: Энергоиздат 1981. – 208 с.
4. Переходные процессы в системах электроснабжения: Учебник / В.Н. Винославский, Г.Г. Пивняк, Л.И. Несен и др.: под ред. В.Н. Винославского. К.: Высш. шк. Головное изд-во, 1989. – 422 с.
5. Петрухин А.Н., Чесноков И.П. Переходные процессы в системах электроснабжения: Учебное пособие. – Киров: Изд-во ВГТУ.- 1999. – 38 с.
6. Жданов П.С. Вопросы устойчивости электрических систем. М.: Энергия, 1979. - 456 с.
7. Павлов Г.М., Меркурьев Г.В. Автоматизация энергосистем. С.Пб.: РАО «ЕЭС России», 2001. – 387 с.
Кафедра Энергетика, автоматика и системы коммуникаций
Факультет Энергетики и систем коммуникаций
Донского государственного технического
университета
Слайд 3Электромеханические переходные процессы
Переходные процессы возникают при переходе электрической системы (ЭС)
от одного режима к другому.
Под режимом системы понимают совокупность процессов,
характеризующих работу электрической системы и ее состояние в любой момент времени.Параметры режима — это напряжения, токи, мощности и т. п. Параметры режима связаны между собой параметрами системы.
Кафедра Энергетика, автоматика и системы коммуникаций
Факультет Энергетики и систем коммуникаций
Донского государственного технического
университета
Слайд 4СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ СЛОЖНЫХ СИСТЕМ
Уравнение движения ротора генератора
Изучение электромеханических переходных
процессов целесообразно начинать с одного из основных уравнений – уравнения
движения ротора генератора. Ротором генератора называют совокупность: ротор турбины, вал и собственно ротор генератора. Движение вращающейся части энергоагрегата – ротора генератора, описывается вторым законом Ньютона.Слайд 5Уравнение движения ротора генератора
Незначительное возмущение в цепи статора генератора вызывает
движение ротора в сторону увеличения или уменьшения угла (это
зависит от знака избыточного момента). Возмущение сообщает ротору некоторое ускорение , которое в относительных единицах пропорционально избыточному моменту и обратно пропорционально постоянной инерции :12.1
Слайд 6Уравнение движения ротора генератора
Здесь принимается, что при небольших изменениях скорости
– постоянная инерции – время, в
течение которого скорость ротора изменяется от нуля до номинальной под действием номинального вращающего момента и при постоянном моменте сопротивления. Постоянная инерции определяется из выражениягде – маховый момент, тм2; – скорость вращения ротора, об/мин;
– номинальная мощность, кВА.
Слайд 7Уравнение движения ротора генератора
Учитывая, что ускорение представляет собой вторую производную
от угла по времени
выражение (12.1) запишем в виде
Слайд 8Уравнение движения ротора генератора
Таким образом, при небольших возмущениях движение ротора
описывается уравнением
, (11.4)где – мощность турбины, – максимальное значение мощности аварийного режима. Момент сопротивления, составляющий около 3 % от номинального момента, как правило, не учитывают.
Слайд 9Уравнение движения ротора генератора
Уравнение (12.4) называется уравнением движения ротора генератора.
Уравнение является нелинейным и не имеет аналитического решения, поэтому при
анализе электромеханических переходных процессов его решают численными методами. Его численное решение в форме описывает изменение угла во времени и позволяет судить об устойчивости генератора. Уравнение (12.4) может иметь различные формы записи в зависимости от того в каких единицах выражены , , и . При незначительных возмущениях в энергосистемах уравнение (12.4) можно линеаризовать и выполнить аналитический анализ.Слайд 10Уравнение движения ротора генератора
Для учёта влияния активного сопротивления в статорной
цепи на электромеханические переходные процессы используется уточнённое уравнение (12.4):
,в котором вторым членом в левой части приближённо учитывается влияние демпферных контуров и внешней электрической сети на движение его ротора. Коэффициент D в этом уравнении, называемый демпферным коэффициентом, обобщённо отражает совокупное влияние всех демпфирующих факторов, а его значение зависит от интенсивности воздействия этих факторов.
Слайд 11Характеристика мощности при сложной связи генератора с системой
В энергосистемах
с электростанциями соизмеримой мощности, представление их одномашинной моделью не позволяет
получить достоверные результаты анализа статической устойчивости энергосистемы. Поэтому в качестве модели для изучения электромеханических переходных процессов используют двух – и трёхмашинные модели.Слайд 12Характеристика мощности при сложной связи генератора с системой
В сложной электрической
системе (содержащей несколько электрических станций) мощность каждой станции, отдаваемая в
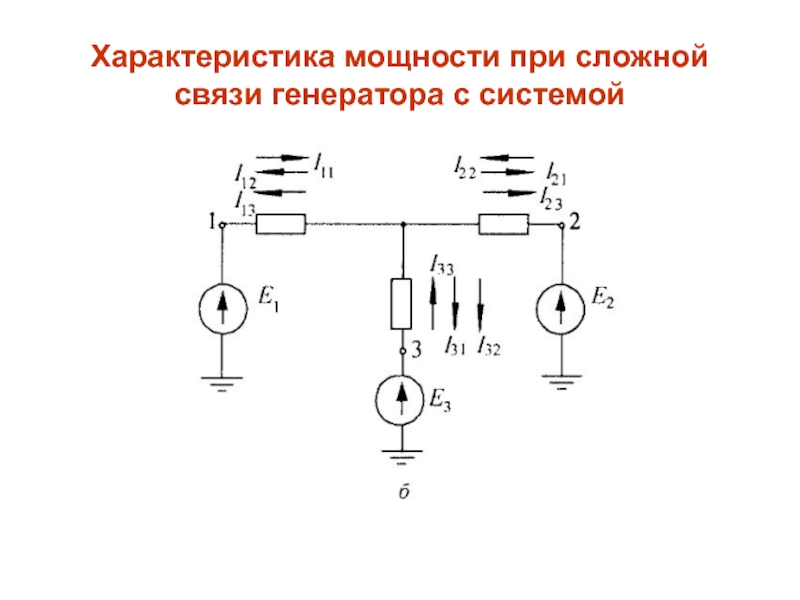
систему, зависит от модулей и сдвигов фаз ЭДС всех генераторов системы. Систему любой сложности можно представить П – образной или Т – образной схемой замещения. Для электрической системы, схема которой приведена на рис. 12.1, а выразим мощность, выдаваемую первой станцией в систему.Слайд 14Характеристика мощности при сложной связи генератора с системой
Для этого воспользуемся
принципом наложения, согласно которому ток, протекающий в обмотке генератора, можно
рассматривать как результат наложения трёх токов. Ток (схема замещения на рис.12.1, б) представляет собой ток, который протекал бы по обмотке этого генератора в том случае, если бы ЭДС остальных генераторов были бы равны нулю. Второй ток вызывается ЭДС генератора 2, если ЭДС генераторов 1 и 3 закорочены. Ток вызывается ЭДС генератора 3 при закороченных ЭДС генераторов 1 и 2.Слайд 16Характеристика мощности при сложной связи генератора с системой
Полный ток в
цепи первого генератора получим путём наложения трёх рассмотренных режимов (рис.12.1,
б).
Составляющие полного тока пропорциональны соответствующим ЭДС. Коэффициенты пропорциональности между ЭДС и током зависят от конфигурации сети и сопротивлений, отдельных её элементов и называются собственными и взаимными проводимостями цепи.
Слайд 17Характеристика мощности при сложной связи генератора с системой
Выражения для составляющих
токов можно представить в виде:
(12.5)где – собственная проводимость; – взаимные проводимости сети.
Учитывая (12.5), выражение для тока первого генератора представим в виде
.
Слайд 18Характеристика мощности при сложной связи генератора с системой
Комплексное значение мощности
определяется умножением сопряжённого комплекса тока на комплекс соответствующей ЭДС
. (12.6)Обозначим фазовые углы векторов ЭДС , и , отсчитываемые относительно произвольной оси (рис. 12.1, в), через , и , а аргументы комплексных собственных и взаимных сопротивлений ветвей
– через
Слайд 20Характеристика мощности при сложной связи генератора с системой
Тогда выражение (12.6)
запишем в виде
где , представляют собой относительные углы ЭДС генераторов 1,2 и 2,3.
Слайд 21Характеристика мощности при сложной связи генератора с системой
Переходя к комплексной
форме записи комплексных величин, получим
Слайд 22Характеристика мощности при сложной связи генератора с системой
Действительная часть этого
выражения характеризует активную мощность, отдаваемую генератором
Слайд 23Характеристика мощности при сложной связи генератора с системой
Если в последнем
выражении вместо аргументов ввести дополняющие их до 90о аргументы
то оно примет вид:(12.7)
Слайд 24Характеристика мощности при сложной связи генератора с системой
Выражение (12.7) позволяет
рассчитать мощность генератора в зависимости от векторов ЭДС, углов расхождения
векторов ЭДС, а также собственных и взаимных проводимостей схемы. Это выражение может быть обобщено на любое количество генераторов:Слайд 25Характеристика мощности при сложной связи генератора с системой
Аналогичным образом можно
записать выражение для мощности любого генератора системы. Так для n–го
генератораСлайд 26Характеристика мощности при сложной связи генератора с системой
Из полученных формул
следует, что для расчёта мощности, отдаваемой генератором в систему, необходимо
знать величины ЭДС всех генераторов системы (модули и аргументы) и комплексные значения собственных и взаимных проводимостей. Модули и аргументы ЭДС вычисляются как параметры нормального режима, предшествующего рассматриваемому переходному режиму. Для определения собственных и взаимных проводимостей выполняют соответствующие расчётыСлайд 27Характеристика мощности при сложной связи генератора с системой
В уравнении (12.7)
свободной существенной переменной, от которой зависят изменяющиеся параметры режима, является
угол . Поэтому в двухмашинных системах можно использовать в качестве практического критерия статической устойчивости:Слайд 28Статическая устойчивость сложных систем
Сложная электрическая система содержит несколько электростанций.
Статическая устойчивость параллельной работы генераторов сложной энергосистемы оценивается по характеру
изменения относительного угла векторов ЭДС генераторов. Для анализа статической устойчивости часто используется метод малых колебаний. Малые колебания в энергосистеме возникают после небольшого возмущения исходного режима.Слайд 29Статическая устойчивость сложных систем
В отличие от рассмотренных ранее методов расчёта
статической устойчивости суть этого метода заключается в исследовании уравнений движения,
записанных в виде уравнений малых отклонений. При установлении простейших условий статической устойчивости (практических критериев) ответ получается только в форме «да – нет», «уйдёт – не уйдёт». При установлении критериев устойчивости, основанных на исследовании уравнений движения – уравнений малых колебаний (малых отклонений), физическая природа происходящих явлений выясняется более полно: устанавливается в любом случае (устойчивость, неустойчивость) характер движения (апериодическое, колебательное – затухающее или нарастающее).Слайд 30Метод малых колебаний
Рассмотрим применение метода малых колебаний для анализа
статической устойчивости системы генератор – шины бесконечной мощности (ШБМ), схема
которой приведена на рис. 12.1, а.При небольших возмущениях движение ротора описывается уравнением (12.4)
.
Слайд 31Метод малых колебаний
Правая часть этого уравнения нелинейна, поэтому уравнение не
имеет аналитического решения. Но при малых отклонениях от положения равновесия
оказывается возможным линеаризовать это уравнение, приведя его к виду дифференциального уравнения с постоянными коэффициентами. Разлагая функцию в ряд Тейлора в области , получим:,
где – малое отклонение угла от исходного значения.
Слайд 32Метод малых колебаний
При малых значениях
можно пренебречь его степенями выше первой. Учитывая, что
, получаем.(12.8)
Слайд 34Метод малых колебаний
Подставив (12.8) и (12.9) в уравнение (12.1), получим
линейное дифференциальное уравнение
.(12.10)
Слайд 36Метод малых колебаний
Решением этого уравнения является изменение во времени
в соответствии с выражением
,где и – корни характеристического уравнения
,
которые равны
.
Слайд 37Метод малых колебаний
При
корни являются чисто мнимыми, при
– чисто вещественными. В случае мнимых корней , где , решение характеристического уравнения будет иметь вид.
Слайд 38Метод малых колебаний
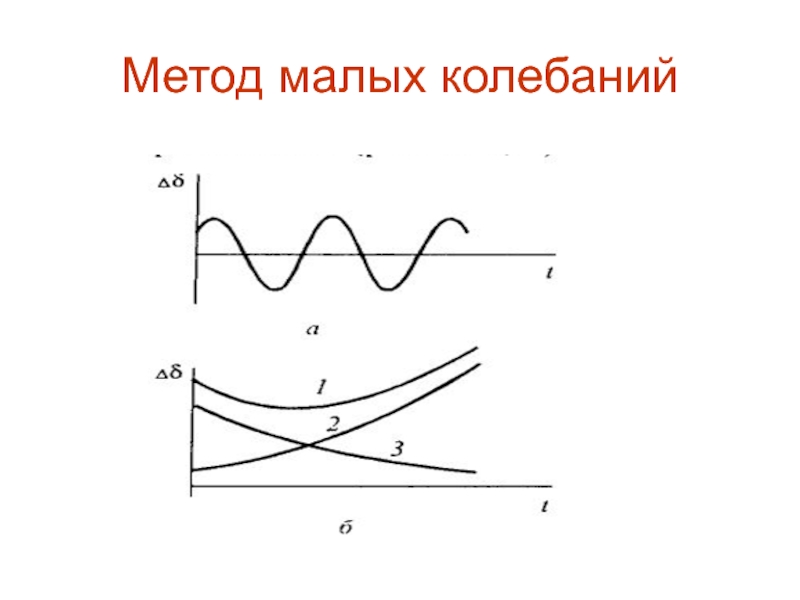
Изменение угла в соответствии с этим выражением происходит
по закону незатухающих гармонических колебаний в окрестности (рис.
12.2, а). Через некоторое время после нарушения исходного состояния установится первоначальный режим. Система в этом случае устойчива.Если корни характеристического уравнения вещественные , то изменение угла носит апериодический характер (9.2, б). Наличие положительного вещественного корня приводит к нарастанию , угол постоянно увеличивается и система оказывается неустойчивой.
Следовательно, необходимым и достаточным условием устойчивости является .
Слайд 40Анализ статической устойчивости сложных систем методом малых колебаний
Сложная электрическая система
содержит несколько электростанций и нагрузок. Предположим, что все нагрузки представлены
постоянными сопротивлениями. В этом случае мощности генераторов выражаются через собственные и взаимные проводимости расчётной схемы:Слайд 41Анализ статической устойчивости сложных систем методом малых колебаний
.(12.10)
Здесь ; и т.д.
Слайд 42Анализ статической устойчивости сложных систем методом малых колебаний
Относительные углы определяются
как разность абсолютных углов, отсчитываемых от произвольно выбранной синхронно вращающейся
оси (рис. 12.3). Если число генераторов в системе равно , то независимыми в (12.10) являются относительных углов . Мощности, выдаваемые генераторами в систему, являются функциями независимых переменных и в общем виде могут быть представлены следующим образомСлайд 44Анализ статической устойчивости сложных систем методом малых колебаний
В системе (12.11)
функции определяются из (12.10) после замены в каждом уравнении всех
относительных углов значениями.
Слайд 45Анализ статической устойчивости сложных систем методом малых колебаний
При возникновении переходного
процесса начинается относительное движение роторов генераторов, описываемое системой уравнений
(12.12)
Слайд 46Анализ статической устойчивости сложных систем методом малых колебаний
Правые части уравнений
могут быть разложены в ряд Тейлора так же, как и
для простейшей системы:. (12.13)
Слайд 47Анализ статической устойчивости сложных систем методом малых колебаний
Знак + и
многоточие в конце каждого уравнения в (12.13) указывают на наличие
членов разложения высших порядков. Отбрасывая эти члены и преобразуя левые части уравнений (12.12) к виду.
Слайд 48Анализ статической устойчивости сложных систем методом малых колебаний
Получаем систему уравнения
малых колебаний системы:
. (12.14)
Слайд 49Анализ статической устойчивости сложных систем методом малых колебаний
Разделив каждое из
уравнений (12.12) на соответствующее значение и вычтя из первого уравнения
поочерёдно все остальные, запишем уравнения малых колебаний в окончательном виде. (12.15)
Слайд 50Анализ статической устойчивости сложных систем методом малых колебаний
Здесь
– относительные ускорения станций, взятых попарно. Запишем систему уравнений (12.15) в операторной форме, обозначая и принимая как алгебраическую величину:
(12.16)
Слайд 51Анализ статической устойчивости сложных систем методом малых колебаний
Признаком неустойчивости системы
является бесконечное увеличение относительных углов . Изменение
абсолютных углов не определяет устойчивости системы, они могут увеличиваться и в устойчивой системе. Система линейных уравнений (12.16) имеет решениеСлайд 52Анализ статической устойчивости сложных систем методом малых колебаний
Поскольку система (12.16)
однородна, ,
следовательно, нетривиальное решение может быть получено только при . Определитель записывается в виде.
Слайд 53Анализ статической устойчивости сложных систем методом малых колебаний
Раскрыв этот определитель,
получим характеристическое уравнение
,корни которого определяют характер изменения относительных углов и, следовательно, определить факт устойчивости или неустойчивости системы.
Слайд 54Критерии устойчивости
В аналитических расчётах статической устойчивости используется другая форма характеристического
уравнения, которая более удобна при использовании известных критериев устойчивости Раусса,
Михайлова и др.:.(12.17)
Слайд 55Критерии устойчивости
Согласно известным теоремам А.М. Ляпунова, для того чтобы система
была устойчива, необходимо и достаточно, чтобы корни характеристического (12.17) имели
отрицательные вещественные части. Определение корней осуществляется прямым решением этого уравнения. При больших степенях уравнения (12.17) используются методы, позволяющие судить по определённым признакам об устойчивости системы без решения характеристического уравнения. Соответствующие признаки называются критериями устойчивости.Слайд 56Критерий устойчивости Гурвица
Согласно критерию Гурвица алгебраическое уравнение n – й
степени с постоянными коэффициентами имеет корни с отрицательными вещественными частями,
если выполняются следующие условия:все коэффициенты уравнения (12.17) положительны;
все определители Гурвица положительны и имеют вид
,
Слайд 58В этих определителях элементы, индекс которых превышает n, заменятся нулями.
Так как в определителе (12.18) последний столбец состоит из одного
коэффициента, отличного от нуля, . При этом условие распадается на два: и . Первое определяет границу апериодической устойчивости, второе – колебательной. Условия п. 1 и 2 зависимы. Если коэффициенты положительны, то все определители Гурвица будут положительны, когда положительны все нечётные определители , , и т.д. Такой критерий называется критерием Льенара-Шипара.Слайд 59Критерий устойчивости Раусса
При анализе статической устойчивости системы первоначально составляется таблица
Раусса, в которой используются коэффициенты характеристического уравнения (12.17).
Слайд 61Критерий устойчивости Раусса
Для того чтобы действительная часть всех корней характеристического
уравнения была отрицательной, необходимо и достаточно, чтобы все элементы первого
столбца таблицы Раусса были отличны от нуля и имели один и тот же знак.Слайд 62Критерий устойчивости Михайлова
Критерий А.В. Михайлова позволяет выразить условия устойчивости электрической
системы в геометрической форме. Приняв
, характеристическое уравнение (12.17) запишем в виде:,
Слайд 64Критерий устойчивости Михайлова
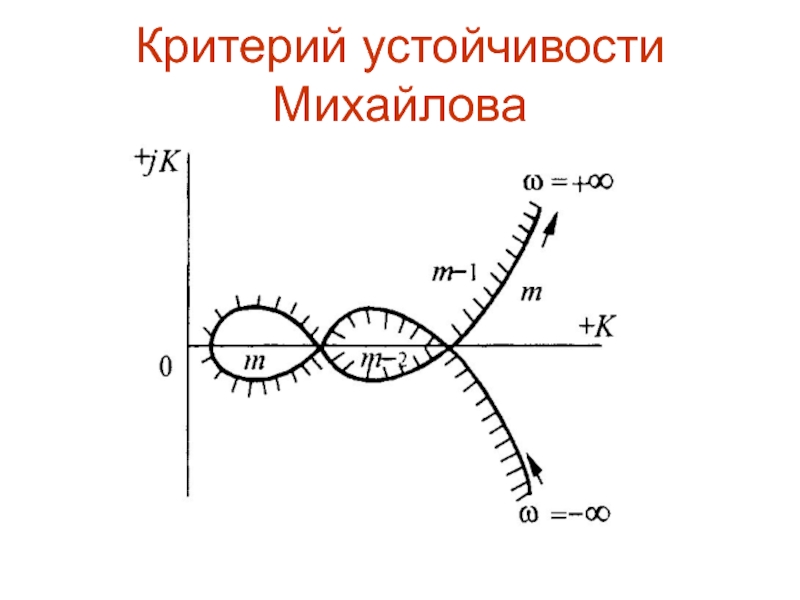
Задавая значения от 0
до , получим для каждого
значения точку на комплексной плоскости. Совокупность точек образует кривую, которая называется годографом характеристического многочлена или годографом Михайлова. Вектор, конец которого при изменении скользит по годографу, называют характеристическим (рис. 12.3).Слайд 67Критерий устойчивости Михайлова
Критерий Михайлова формулируется следующим образом: для того чтобы
характеристическое уравнение имело только корни с отрицательной вещественной частью, необходимо
и достаточно, чтобы характеристический вектор при изменении от 0 до монотонно поворачивался против часовой стрелки на угол , где – степень характеристического уравнения. Модуль характеристического вектора при всех значениях должен быть отличным от нуля.Слайд 68Метод D – разбиения
Метод D – разбиения применяется в том
случае, когда необходимо выявить влияние на устойчивость каких-либо параметров системы
(например, коэффициентов усиления регулятора возбуждения). С помощью метода D – разбиения решается задача определения значений выбираемых коэффициентов усиления, при которых характеристическое уравнение автоматически регулируемой системы имеет только корни с отрицательной вещественной частью. При этом в зависимости от количества параметров различают методы D – разбиения – по одному, двум и более параметрам.Слайд 69Метод D – разбиения
Метод D – разбиения по одному параметру.
Если некоторые коэффициенты характеристического уравнения (9.17) линейно зависят от параметра
системы автоматического регулирования, то это уравнение можно представить в виде,(12.19)
где – совокупность членов, не зависящих от .
Слайд 70Метод D – разбиения
Если в (12.19) принять
, то
.Придавая значения в пределах от до с определённым интервалом , вычисляют значения . Кривую, построенную по этим значениям в комплексной плоскости параметра , называют границей D – разбиения плоскости рассматриваемого параметра или D – кривой. На рис 12.4 показана граница D – разбиения. При всех значениях параметра , находящегося на D – кривой, характеристическое уравнение имеет один мнимый корень.
Слайд 71Метод D – разбиения
Таким образом, D – кривая это отображение
мнимой оси комплексной плоскости корней на плоскость параметра
. Граница D – разбиения делит плоскость параметра на области с одинаковым числом корней, имеющих положительные вещественные части. Для выделения областей, имеющих одно и то же число таких корней, граница D – разбиения штрихуется. Штриховка наносится слева при движении по кривой от до .Слайд 72Метод D – разбиения
Если параметр , изменяясь, пересекает D
– кривую с заштрихованной стороны, то характеристическое уравнение теряет один
корень, расположенный в левой полуплоскости, и приобретает один корень, расположенный в правой. Пересечение D – кривой с незаштрихованной стороны, наоборот, означает появление одного корня, расположенного в левой полуплоскости, и потерю корня в правой. После штриховки проводят разметку D – разбиения. Для этого выбирают любую область и помечают её буквой m, считая, что m есть число корней в правой полуплоскости для данной области.Слайд 73Метод D – разбиения
Перемещаясь из этой области в соседнюю, пересекая
при этом D – кривую, соседнюю область помечают как m
+1, если пересечение произошло с заштрихованной стороны, или m -1, если пересечение произошло с незаштрихованной стороны на заштрихованную. Затем выбирают такую область, которой соответствует наименьшее число корней характеристического уравнения в правой полуплоскости. Эта область считается претендентом на область устойчивости. Чтобы окончательно это проверить является ли данная область значений параметра областью устойчивости, необходимо задаться значением в этой области, подставить его в характеристическое уравнение и проверить характер корней этого уравнения по какому-либо рассмотренному ранее критерию. Физический смысл имеют лишь действительные значения . Поэтому окончательный вывод об устойчивости даётся для значений , лежащих на оси абсцисс.Слайд 74Влияние промежуточных подключений на статическую
устойчивость генератора
При средней и большой дальности
передачи электрической энергии (200 км и более) в промежуточных точках
линий, как правило, подключаются различные элементы и части энергосистемы. Это могут быть шунтирующие реакторы, ёмкостные поперечные компенсирующие устройства (конденсаторные батареи), управляемые источники реактивной мощности, подстанции с промежуточной электрической нагрузкой либо с местными энергосистемами малой мощности.Слайд 75Влияние промежуточных подключений на статическую
устойчивость генератора
Эти подключения оказывают влияние на
статическую устойчивость электропередач, что выражается в увеличении или уменьшении пределов
статической устойчивости.Оценим такое влияние наиболее распространённых подключений, полагая, что они представляются пассивными элементами в схеме замещения одномашинной энергосистемы.
Слайд 76Влияние промежуточных подключений на статическую
устойчивость генератора
Взаимные сопротивления
и определяются как отношения ЭДС в одной ветви к
току в другой и поэтому в физическом смысле не являются сопротивлениями. Их следует рассматривать как комплексные коэффициенты пропорциональности между токами и ЭДС, у которых в зависимости от структуры и параметров пассивной части схемы замещения могут быть получены соотношения:, , .
Слайд 77Влияние промежуточных подключений на статическую
устойчивость генератора
Выражения (12.10), (12.11) для одномашинной
системы запишем в компактной форме:
;(12.20), (12.21)
где , – собственные мощности со стороны генератора и приёмной системы; – максимум взаимных мощностей генератора и приёмной системы.
Слайд 78Влияние промежуточных подключений на статическую
устойчивость генератора
Как видно из (12.20) и
(12.21), синусоидальные зависимости взаимных мощностей от угла на входе и
выходе пассивной части схемы замещения одинаковы по амплитуде и имеют равные по абсолютной величине, но различные по знаку фазовые сдвиги относительно оси ординат.Напомним, что каждое из собственных и
сопротивлений и определяется как отношение ЭДС к току, которые действуют в одной и той же ветви. По этому признаку собственные сопротивления являются, в физическом смысле, активно–реактивными сопротивлениями, у которых:
, , , , , .
Слайд 79Влияние активного сопротивления на характеристику мощности
Построим угловые характеристики мощности генератора
c неизменной ЭДС, от которого передаётся мощность через электрическую сеть,
представленную в виде активного и индуктивного сопротивлений (рис. 12.4). В этом случае все собственные и взаимные проводимости равны между собой, и для их составляющих введём единые обозначения:;
.
Слайд 80Влияние активного сопротивления на характеристику мощности
Тогда выражения (12.20) и (12.21)
запишем в виде:
;(12.22)
.(12.23)
Слайд 81Влияние активного сопротивления на характеристику мощности
Предел по статической устойчивости генератора,
определяемый по условию
, обозначен точкой на характеристике мощности . Максимум соответствует углу и вычисляется как.
Слайд 82Влияние активного сопротивления на характеристику мощности
Разность
представляет собой зависимость потерь активной мощности на
сопротивлении от угла. Если принять , то будет получено: , . При этом характеристики мощности и будут определяться выражением.
Слайд 83Влияние активного сопротивления на характеристику мощности
Угловые характеристики мощности
Схема замещения
простейшей
энергосистемы с учётом активного
сопротивления
Слайд 84Влияние активной нагрузки
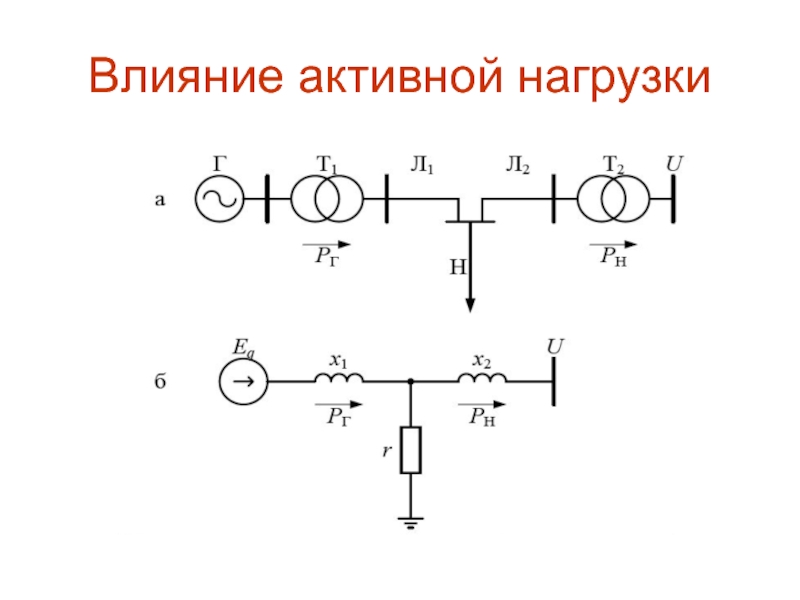
Положим, что промежуточная нагрузка Н (рис. 12.6, а),
работающая с коэффициентом мощности равным единице, представлена в схеме замещения
активным сопротивлением (рис. 12.6, б). Поскольку эта схема имеет Т–образный вид с элементами , , , то для её обобщённые параметры найдём с помощью приведенных в п. 12.2 выражений:(12.24)
Слайд 87Влияние активной нагрузки
Для активно–индуктивной цепи аргументы собственных сопротивлений составляют
, .
Поэтому соответствующие дополняющие углы положительны: , . Аргумент взаимных сопротивлений , в данном случае находится в интервале углов от до , так как вещественная составляющая этих сопротивлений . Соответственно, дополняющий угол .Слайд 88Влияние активной нагрузки
На рис. 12.7 показаны угловые характеристики мощности
, , построенные
по выражениям:;
.
Здесь же для сравнения приведена характеристика
для случая, когда промежуточная нагрузка отключена, то есть когда .
Слайд 89Влияние активной нагрузки
Характеристики мощности, при наличии поперечного активного сопротивления
Слайд 90Влияние активной нагрузки
При подключении активной нагрузки в промежуточной точке линии
электропередачи максимум характеристики мощности генератора
смещается относительно угла влево на угол , а максимум характеристики смещается на такой же угол вправо. При последовательном включении активного сопротивления наблюдалась обратная картина.Слайд 91Влияние активной нагрузки
При подключении активной нагрузки происходит промежуточный отбор мощности.
Его можно определить как разность
,зависящую от угла . Наличие этого отбора приводит к увеличению предельной статической устойчивости мощности генератора. Однако при этом уменьшаются возможности передачи мощности в приёмную систему. Поэтому можно говорить о неоднозначном влиянии промежуточной активной нагрузки на статическую устойчивость генератора одномашинной энергосистемы.
Слайд 92Влияние шунтирующего реактора
Шунтирующие реакторы (ШР) используются в высоковольтных электрических сетях
для компенсации избыточной реактивной мощности, генерируемой линиями электропередачи. Реакторы подключаются
наглухо или через выключатели в концевых точках линий электропередачи длиной свыше 300 км для предотвращения появления перенапряжений при коммутационных переключениях. В некоторых случаях реакторы подключаются к шинам высшего напряжения станционных и сетевых подстанций.Слайд 93Влияние шунтирующего реактора
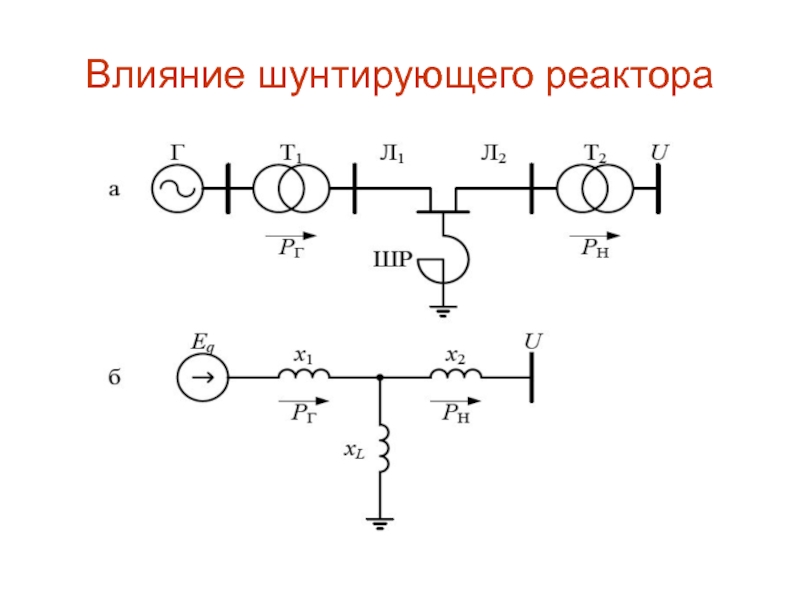
Подключение ШР в промежуточной точке электрической связи одномашинной
энергосистемы (рис. 12.8, а) вносит дополнительное индуктивное сопротивление в схему
замещения (рис. 12.8, б), что отражается на обобщённых параметрах , и .Слайд 95Влияние шунтирующего реактора
При пренебрежении активными сопротивлениями элементов энергосистемы, сопротивления элементов
схем замещения элементов и обобщённые параметры не содержат вещественных частей:
; ; ;
; ; .
Слайд 96Влияние шунтирующего реактора
Поэтому дополняющие углы ,
и равны нулю, а зависимости
, совпадают и выражаются одной формулой.
Слайд 97Влияние шунтирующего реактора
Первоначально рассмотрим случай, когда ШР отключён.
В этом случае
взаимное сопротивление
и соответствующий предел мощности
определяется как:,
.
Слайд 98Влияние шунтирующего реактора
Во втором случае на аналогичные параметры
, оказывает влияние индуктивное сопротивление реактора
, что выражается в виде:;
,
где .
Слайд 99Влияние шунтирующего реактора
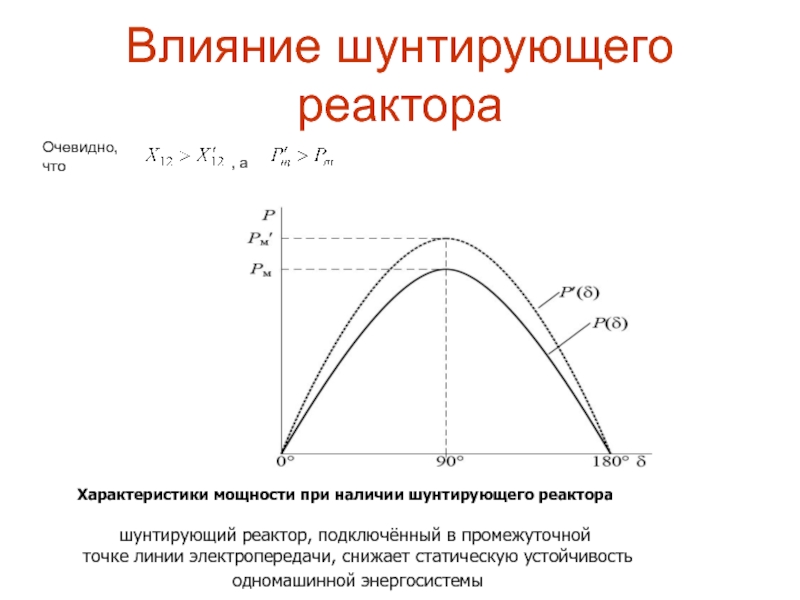
Очевидно, что
, а
Характеристики мощности при
наличии шунтирующего реактора
шунтирующий реактор, подключённый в промежуточной
точке линии
электропередачи, снижает статическую устойчивостьодномашинной энергосистемы
Слайд 100Влияние конденсаторной батареи
Конденсаторные батареи (КБ) иногда устанавливаются и подключаются в
промежуточных точках линий электропередачи с целью поддержания нормальных уровней напряжения
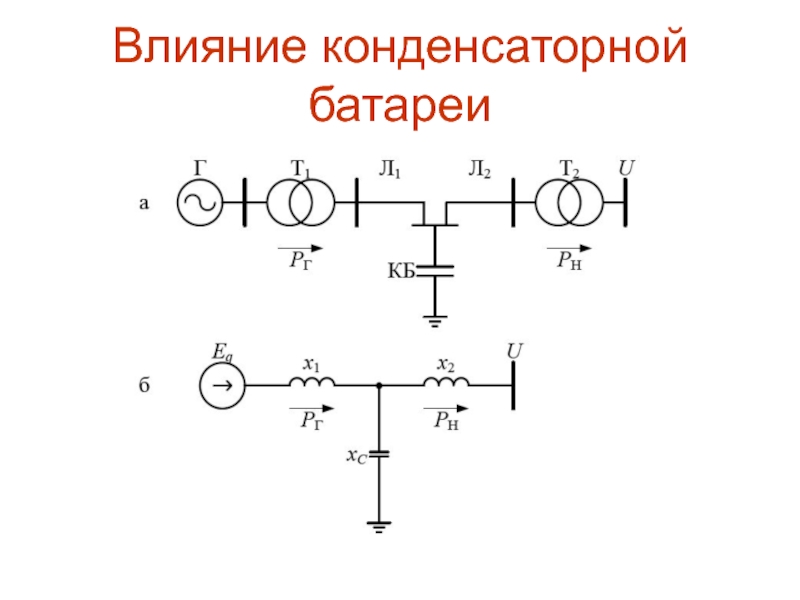
при передаче больших потоков мощности. Оценим влияние КБ на статическую устойчивость одномашинной энергосистемы при таких же расчётных условиях, что и в предыдущих случаях (рис. 12.10, а, б).Слайд 102Влияние конденсаторной батареи
Подключённая КБ в схеме замещения энергосистемы (рис. 12.10,
б) имеет отрицательное реактивное сопротивление
,которое оказывает влияние на взаимное сопротивление и предел мощности определяется по выражениям:
;
,
где .