Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы комбинаторики
Содержание
- 1. Элементы комбинаторики
- 2. Комбинаторика– Комбинаторика — раздел математики, посвящённый решению
- 3. История возникновенияКомбинаторика возникла в XVI веке. В
- 4. Готфрид Вильгельм ЛейбницВсемирно известный немецкий учёный, занимался
- 5. Основные правила комбинаторикиПравило сложения (суммы)Если объект А
- 6. Основные правила комбинаторикиЗадача. В магазине есть 5
- 7. Основные правила комбинаторикиПравило умножения (произведения)Если объект А
- 8. Основные правила комбинаторикиЗадача. Сколько различных обедов П.И. Чичиков
- 9. Основные правила комбинаторики322=12 различных обедов
- 10. Дерево всевозможных вариантовЗадача. Несколько стран в качестве
- 11. Дерево всевозможных вариантовфлаг
- 12. ФакториалОт (англ.) factor – множитель.Произведение первых подряд
- 13. РазмещенияПусть дано множество, состоящее из n элементов.
- 14. ПерестановкиПерестановкой для n-элементного множества называется n-элементное размещение.или:Перестановкой
- 15. СочетанияПусть дано множество, состоящее из n элементов.
- 16. Слайд 16
- 17. Задача. В семье 6 человек, а за
- 18. Слайд 18
- 19. Задача: Имеются пять предметов для подарков. Сколькоможно
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Задача: В группе 20 студентов, из которых
- 24. Скачать презентанцию
Комбинаторика– Комбинаторика — раздел математики, посвящённый решению задач выбора и расположения элементов некоторого множества, подчиненных определённым условиям.Комбинаторные методы применяются в теории кодирования, планировании эксперимента, топологии, математической логике, теории игр, кристаллографии, биологии,
Слайды и текст этой презентации
Слайд 2Комбинаторика
– Комбинаторика — раздел математики, посвящённый решению задач выбора и
расположения элементов некоторого множества, подчиненных определённым условиям.
теории кодирования, планировании эксперимента, топологии, математической логике, теории игр, кристаллографии, биологии, статистической физике, экономике и т.д. Комбинаторика является основой для изучения теории вероятностей и математической статистики.Слайд 3История возникновения
Комбинаторика возникла в XVI веке. В то время в
жизни привилегированных слоев общества большое место занимали азартные игры (карты,
кости). Были широко распространены лотереи. Возникали вопросы: сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей? Эти и другие проблемы оказались движущей силой в развитии комбинаторики.Теоретические исследования вопросов комбинаторики предприняли Паскаль и Ферма, Бернулли, Лейбниц и Эйлер и др.
Слайд 4Готфрид Вильгельм Лейбниц
Всемирно известный немецкий учёный, занимался философией, математикой, физикой,
организовал Берлинскую академию наук и стал её первым президентом.
В
1666 году вводит термин "комбинаторика" в своей диссертации об искусстве комбинаторики, в которой решает основные комбинаторные задачи. 1.07.1646 - 14.11.1716
Слайд 5Основные правила комбинаторики
Правило сложения (суммы)
Если объект А может быть выбран
n способами, а объект В – m способами, то выбор
«или А, или В» может быть осуществлен n+m способами.Задача. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Решение: 5 + 4 = 9
Слайд 6Основные правила комбинаторики
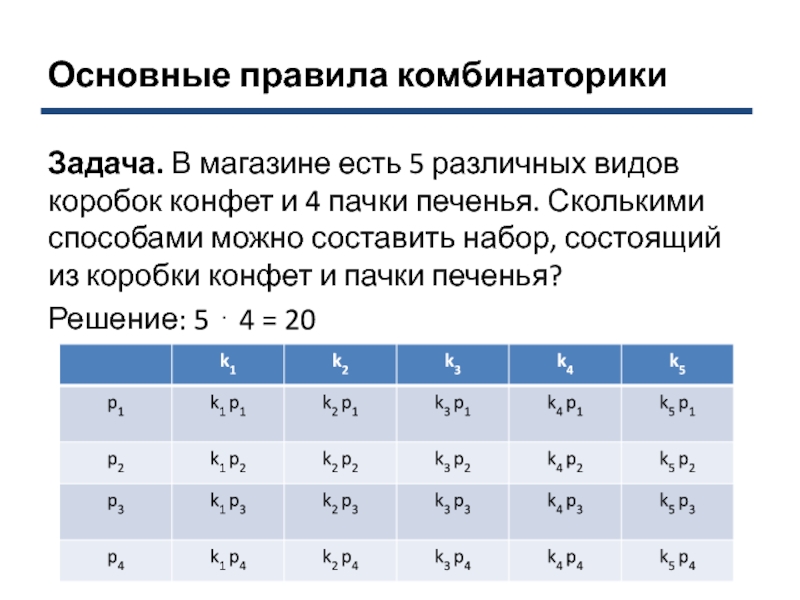
Задача. В магазине есть 5 различных видов коробок
конфет и 4 пачки печенья. Сколькими способами можно составить набор,
состоящий из коробки конфет и пачки печенья?Решение: 5 4 = 20
Слайд 7Основные правила комбинаторики
Правило умножения (произведения)
Если объект А может быть выбран
n способами и после каждого из таких выборов объект В
– m способами, то выбор «А и В» в указанном порядке может быть осуществлен n m способами.Слайд 8Основные правила комбинаторики
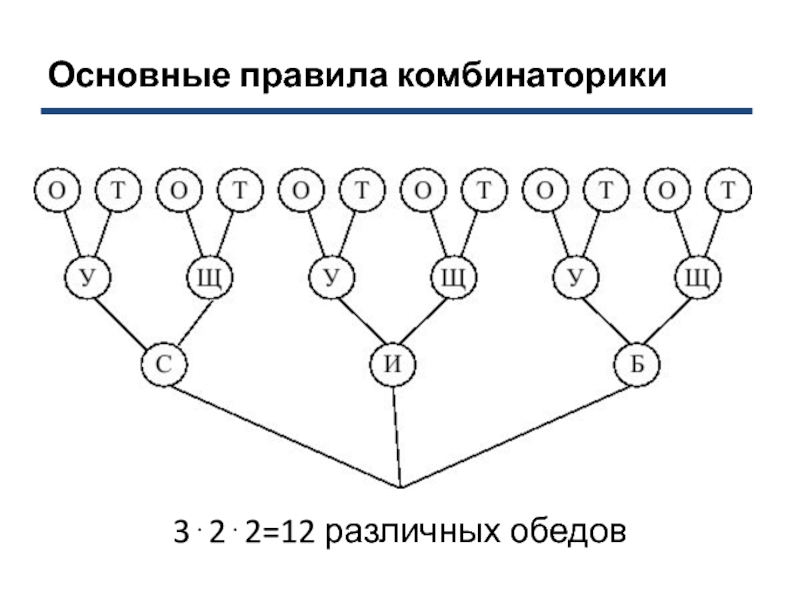
Задача. Сколько различных обедов П.И. Чичиков мог насчитать из
блюд, выставленных на столе у П.П. Петуха, если бы на каждый
обед выбирать только одно холодное блюдо, одно первое блюдо и одно второе блюдо? На столе у П.П. Петуха на этот раз были выставлены из холодных блюд студень с хреном, свежая икра, свежепросоленная белужина; на первое - уха из стерлядей, щи с грибами; на второе - осетрина жареная, теленок, жаренный на вертеле.Слайд 10Дерево всевозможных вариантов
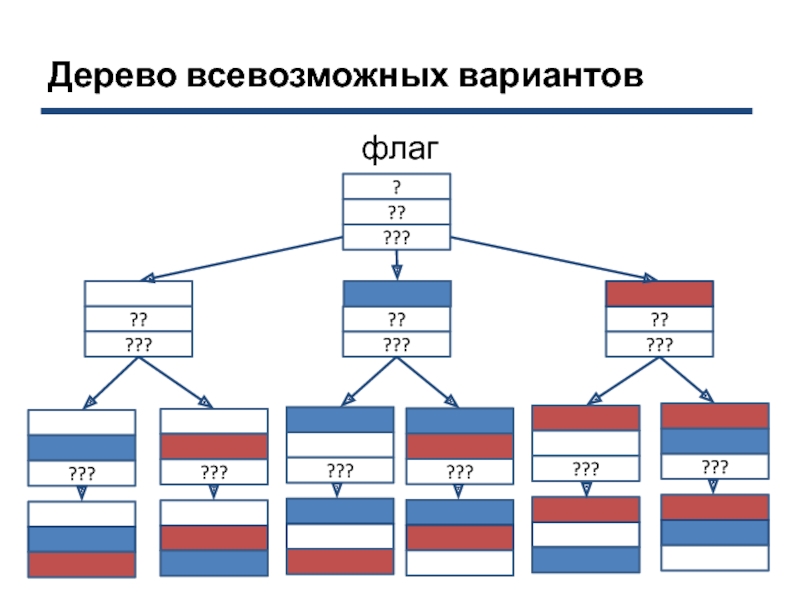
Задача. Несколько стран в качестве символа своего государства
решили использовать флаг в виде горизонтальных полос одинаковых по ширине,
но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других флаг?Чем данная задача отличается от предыдущей?
Слайд 12Факториал
От (англ.) factor – множитель.
Произведение первых подряд идущих n натуральных
чисел называют факториалом и обозначают через n!
n! = 123…(n2)(n1)n
0! =
11! = 1
2! = 12 = 2
3! = 123 = 6
4! = 1234 = 24 и т.д.
Овчинникова Р.П.Элементы дискретной математики
Слайд 13Размещения
Пусть дано множество, состоящее из n элементов.
Размещением из n-элементного
множества по k (0 kn) элементов называется k-элементное подмножество, в
котором важен порядок расположения элементов.Пример. {1,2,3,4,5} – n=5 элементов
Размещения по k=1: 1, 2, 3, 4, 5
Размещения по k=2: 12, 13, 14, 15, 21, 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54
Размещения по k=3: 123, 124, 125, 132, 134, 135, 142, 143, 145, 152, 153, 154, …512, 513, 514, 521, 523, 524, 531, 532, 534, 541, 542, 543
Размещения по k=4: 1234, 1235, 1243, 1245, 1324, 1325, …
Слайд 14Перестановки
Перестановкой для n-элементного множества называется n-элементное размещение.
или:
Перестановкой называют упорядоченную выборку
элементов из некоторого множества.
Пример. {1,2,3,4,5} – n=5 элементов
Перестановки: 12345,
12354, 12435, 12453, 12534, 12543, 13245, 13254, 13425, 13452, 13524, 13542, …Слайд 15Сочетания
Пусть дано множество, состоящее из n элементов.
Сочетанием из n-элементного
множества по k (0 kn) элементов называется k-элементное подмножество, в
котором не важен порядок расположения элементов.Пример. {1,2,3,4,5} – n=5 элементов
Сочетания по k=1: {1}, {2}, {3}, {4}, {5}
Сочетания по k=2: {1,2}, {1,3}, {1,4}, {1,5}, {2,3}, {2,4}, {2,5}, {3,4}, {3,5}, {4,5}
Сочетания по k=3: {1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}
Сочетания по k=4: {1,2,3,4}, {1,2,3,5}, {1,2,4,5}, {1,3,4,5}, {2,3,4,5}
Слайд 17Задача. В семье 6 человек, а за столом в кухне
6 стульев. Было решено каждый вечер перед ужином рассаживаться на
эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?№1
№2
№3
№4
№5
№6
6
5
4
3
2
1
6•5•4•3•2•1=
720дн.
-почти 2 года
Слайд 19Задача: Имеются пять предметов для подарков. Сколько
можно составить различных подарочных
наборов из двух предметов?
С помощью перечисления: ab, ac, ad, af,
bc, bd, bf, cd, cf, df — 10 наборов. По формуле: порядок предметов здесь не важен и элементы повторятся не могут, поэтому число различных наборов равноСлайд 23Задача: В группе 20 студентов, из которых 5 отличников, 11
хорошистов и остальные троечники. Сколькими способами можно выбрать группу для
выполнения лабораторной работы, состоящей из 3 хорошистов, 1 отличника и 1 троечника.Задача: Имеется 4 чашки, 5 блюдец, 6 ложек (все чашки, блюдца, ложки различны). Сколькими способами можно накрыть стол к чаю на 3 человека, если каждый получает 1 чашку, 1 блюдце и 1 ложку.