Слайд 2Определение
Совокупность всех направленных отрезков, для которых введены операции:
- сравнения
- сложения
- умножения на вещественное число
называется множеством векторов.
Конкретный
элемент этого множества будем называть вектором и обозначать символом с верхней стрелкой,
например
Слайд 3Определения
Отрезок прямой, концами которого служат лежащие на ней точки
A и B, называется направленным отрезком, если указано, какая из
этих двух точек является началом и какая - концом отрезка.
Направленный отрезок, начало и конец которого совпадают, называется нулевым направленным отрезком.
Длиной (модулем) вектора называется расстояние между началом и концом вектора.
Слайд 4Действия с направленными отрезками
Определение: Два ненулевых и
направленных отрезка и при
называются равными, если они
- лежат на параллельных
прямых;
- точки B и D лежат по одну сторону от прямой, проходящей через точки A и C;
- имеют равные длины, т.е.
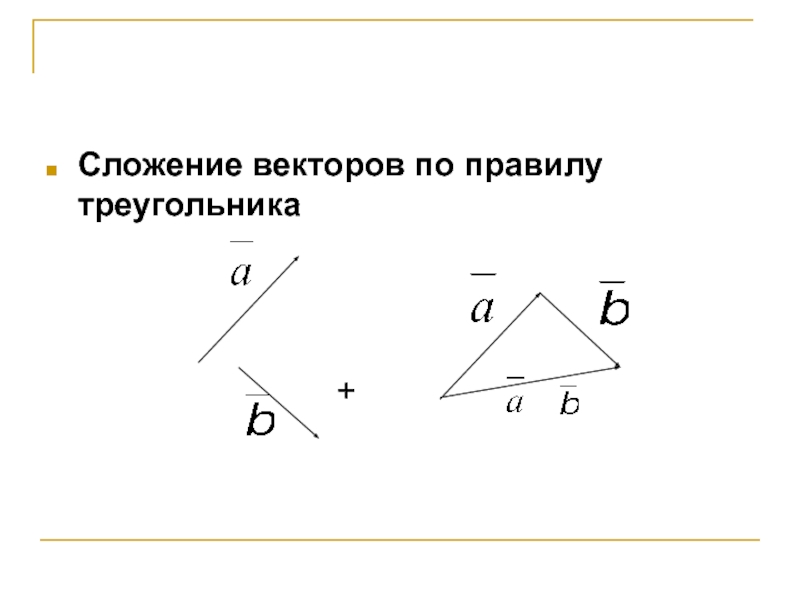
Слайд 5Сложение векторов по правилу треугольника
+
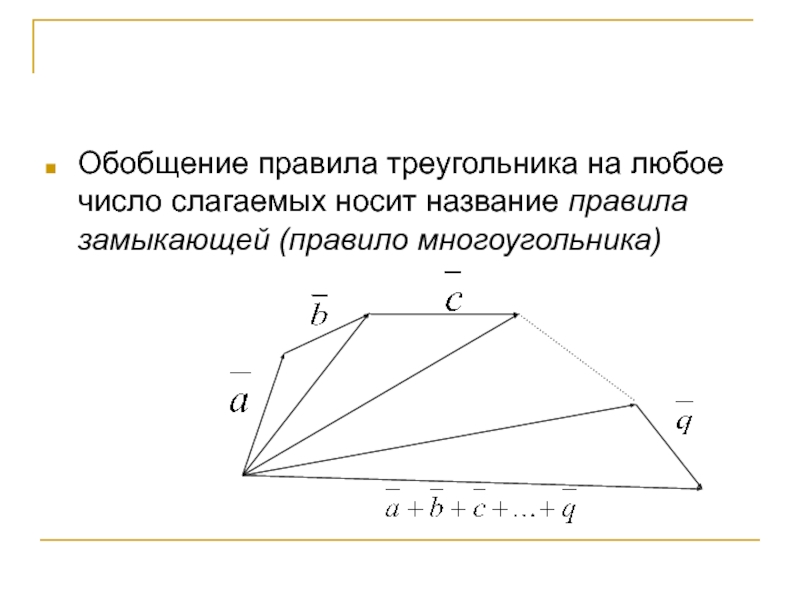
Слайд 6Обобщение правила треугольника на любое число слагаемых носит название правила
замыкающей (правило многоугольника)
Слайд 7Операция сложения направленных отрезков может быть выполнена по правилу параллелограмма
Слайд 8Разностью - направленных отрезков называется направленный отрезок , удовлетворяющий равенству
= + .
Для того, чтобы построить разность векторов можно построить
сумму векторов и (- )
Любой направленный отрезок при сложении с нулевым не изменяется.
Слайд 9При умножении вектора на число λ получается вектор, длина которого
равна
Слайд 10Операции сложения и умножения на вещественное число на множестве векторов
обладают свойствами:
1. Коммутативности
2. Ассоциативности
3. Дистрибутивности
для любых векторов
и
любых вещественных чисел и .
Слайд 11Определение. Два вектора, параллельные одной и той же прямой, называются
коллинеарными.
Три вектора, параллельные одной и той же плоскости, называются компланарными.
Нулевой вектор считается коллинеарным любому другому вектору. Нулевой вектор считается компланарным любой паре векторов.
Слайд 12Линейная зависимость векторов
Определение. Выражение вида
, где некоторые числа,
называется линейной комбинацией векторов
Слайд 13Линейная зависимость векторов
Определение. Векторы
называются линейно зависимыми, если существует
их нетривиальная линейная комбинация
Определение. Векторы
называются линейно независимыми, если из
условия следует тривиальность линейной комбинации
такая, что
Слайд 14Свойства линейно независимых векторов
1. Один вектор линейно независим тогда и
только тогда, когда он ненулевой.
2. Два вектора линейно независимы тогда
и только тогда, когда они неколлинеарны.
3. Три вектора линейно независимы тогда и только тогда, когда они некомпланарны.
Если среди векторов имеется подмножество линейно зависимых, то и все векторы
линейно зависимы.
Если среди векторов имеется хотя бы один нулевой, то векторы линейно зависимы.
Слайд 15Базис в пространстве векторов
Определение:
Базисом в пространстве векторов называется набор линейно
независимых векторов
Слайд 16Определение
Базисом на прямой называется любой ненулевой вектор, принадлежащий этой
прямой.
Базисом на плоскости называется любая упорядоченная пара линейно независимых
векторов, принадлежащих этой плоскости.
Базисом в пространстве называется любая упорядоченная тройка линейно независимых векторов.
Определение Базис называется ортогональным, если образующие его векторы попарно ортогональны (взаимно перпендикулярны).
Определение Ортогональный базис называется ортонормированным, если образующие его векторы имеют единичную длину.
Слайд 17Координаты вектора:
Пусть дан базис тогда любой вектор в пространстве может быть представлен,
и притом единственным образом, в виде
где - некоторые числа (коэффициенты разложения),
которые называют координатами данного вектора в заданном базисе.
Слайд 18Координаты вектора:
Для записи вектора
в координатном представлении используются формы:
Слайд 19Операции с векторами в координатном представлении:
Сравнение векторов: Два вектора и
равны тогда и только тогда, когда равны их соответствующие координаты
Сложение векторов : При сложении двух векторов их соответствующие координаты складываются.
Умножение вектора на число: При умножении вектора на число, на это число умножаются все координаты вектора.
Слайд 20Условия линейной зависимости и независимости векторов в координатном представлении
Для
того чтобы два вектора
на плоскости были линейно зависимы, необходимо
и достаточно, чтобы их координаты в некотором базисе удовлетворяли условию
Слайд 21Условия линейной зависимости и независимости векторов в координатном представлении
Для
того чтобы три вектора
в пространстве были линейно зависимы, необходимо
и достаточно, чтобы их координаты в некотором базисе удовлетворяли условию
Слайд 22Замечание:
Равенства
и
соответственно являются необходимыми и достаточными условиями коллинеарности пары
векторов на плоскости и компланарности тройки векторов в пространстве.
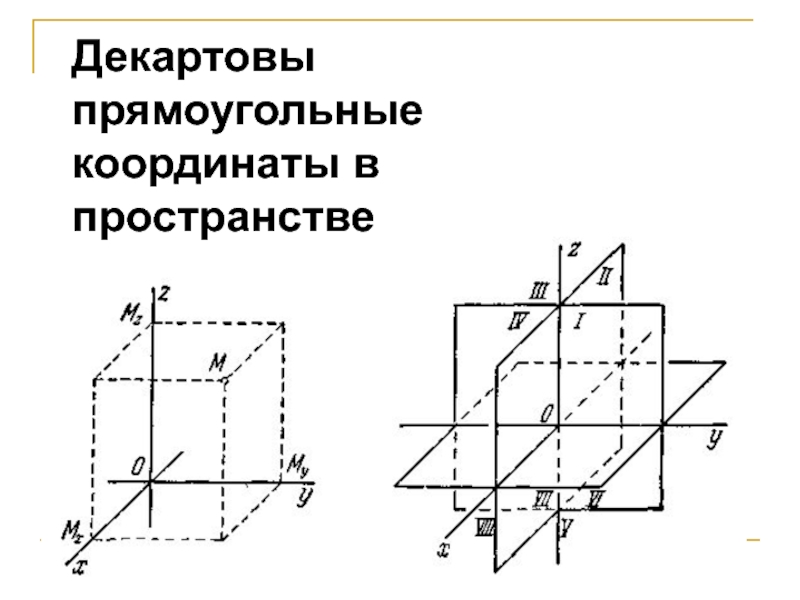
Слайд 23Декартова система координат.
Определение. Декартовой системой координат в пространстве называется
совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие
через начало координат называются осями координат.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат. Будем обозначать векторы базиса .
Слайд 24Декартовы прямоугольные координаты в пространстве
Слайд 25Основные формулы:
Если заданы точки А(x1, y1, z1), B(x2, y2,
z2), то координаты вектора определяются по формуле:
= (x2 – x1,
y2 – y1, z2 – z1).
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве
А(х1, y1, z1), B(x2, y2, z2), то:
Слайд 26Основные формулы:
Если точка М(х, у, z) делит отрезок АВ в
соотношении /, считая от А, то координаты этой точки определяются
как:
В частном случае координаты середины отрезка находятся как:
x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.
Слайд 27Скалярное произведение векторов.
Определение. Скалярным произведением векторов называется число, равное
произведению длин этих сторон на косинус угла между ними.
= cos
Если рассматривать векторы
в декартовой прямоугольной системе координат, то
= xa xb + ya yb + za zb;
Слайд 28Формула для вычисления угла между векторами:
Слайд 29Свойства скалярного произведения векторов
1) =
2;
2)
= 0, если
или = 0 или = 0.
3) = ;
4) ( + ) = + ;
5) (m ) = ( m) = m( ); m=const
Слайд 30Векторное произведение векторов.
Три некомпланарных вектора
взятые в указанном порядке
образуют правую тройку, если с конца третьего вектора кратчайший поворот
от первого вектора ко второму виден совершающимся против часовой стрелки, и левую - если по часовой.
Слайд 32Векторное произведение векторов.
Векторным произведением векторов
и
называется вектор
удовлетворяющий
следующим условиям:
1)
где - угол между векторами
2)
вектор
ортогонален векторам
и
3)
образуют правую тройку векторов.
Слайд 33Векторное произведение векторов:
Обозначается: или
Геометрическим смыслом длины векторного произведения векторов является площадь
параллелограмма, построенного на векторах
Слайд 34Свойства векторного произведения векторов:
1) ;
2) ,
если
или
= 0 или = 0;
3) (m ) = (m ) = m( );
4) ( + ) = + ;
Слайд 35Векторное произведение векторов
Если заданы векторы
(xa, ya, za) и
(xb, yb, zb)
=
в декартовой
прямоугольной системе координат с единичными векторами , то
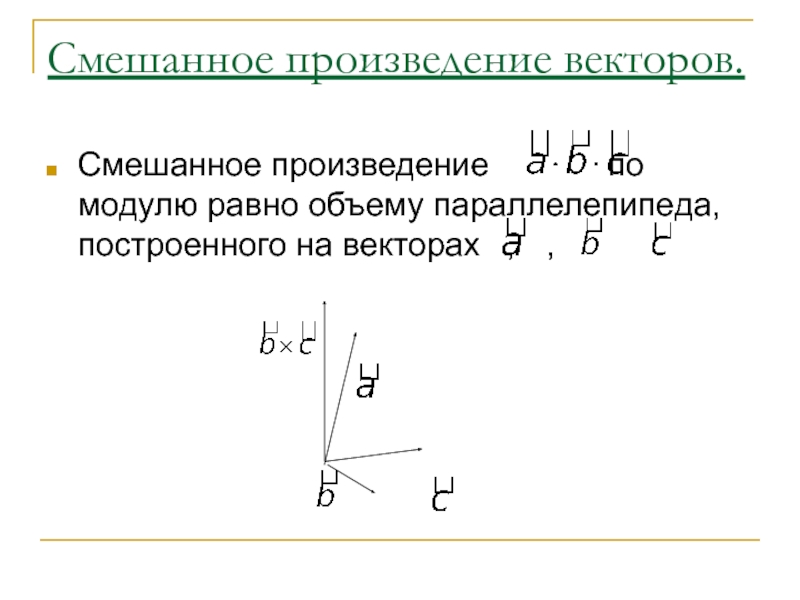
Слайд 36Смешанное произведение векторов.
Определение. Смешанным произведением векторов , и называется
число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов
и
Обозначается или ( , , )
Слайд 37Смешанное произведение векторов.
Смешанное произведение по модулю равно объему параллелепипеда,
построенного на векторах , ,
Слайд 38Свойства смешанного произведения векторов.
1)Смешанное произведение равно нулю, если:
а) хоть
один из векторов равен нулю;
б) два из векторов коллинеарны;
в) векторы
компланарны.
2)
3)
4)
5) Объем треугольной пирамиды, образованной векторами , , равен
Слайд 39Свойства смешанного произведения векторов:
6) Если ,
то