Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: исследование функции с помощью производной
Содержание
- 1. Тема: исследование функции с помощью производной
- 2. Чтобы построить график функции, необходимо исследовать ее
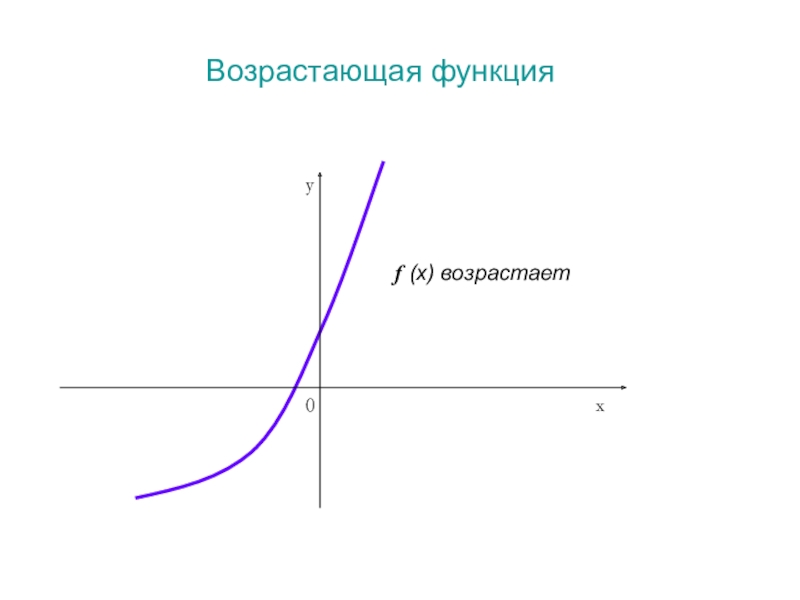
- 3. Возрастающая функцияf (x) возрастает
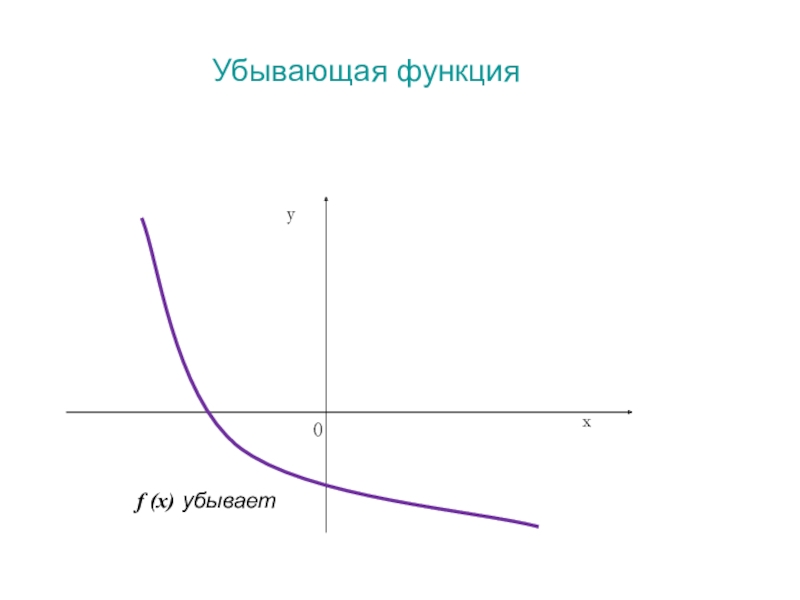
- 4. Убывающая функцияf (x) убывает
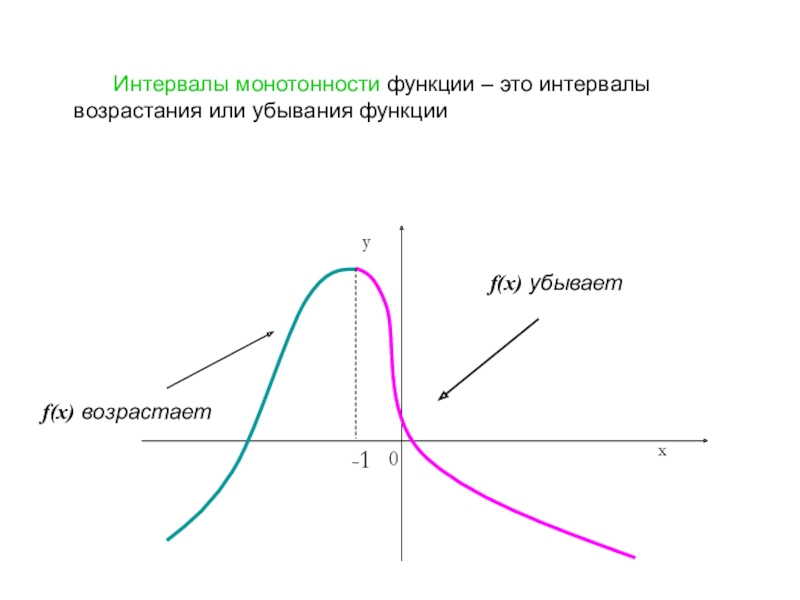
- 5. Интервалы монотонности функции – это интервалы возрастания или убывания функцииf(x) возрастаетf(x) убывает-1
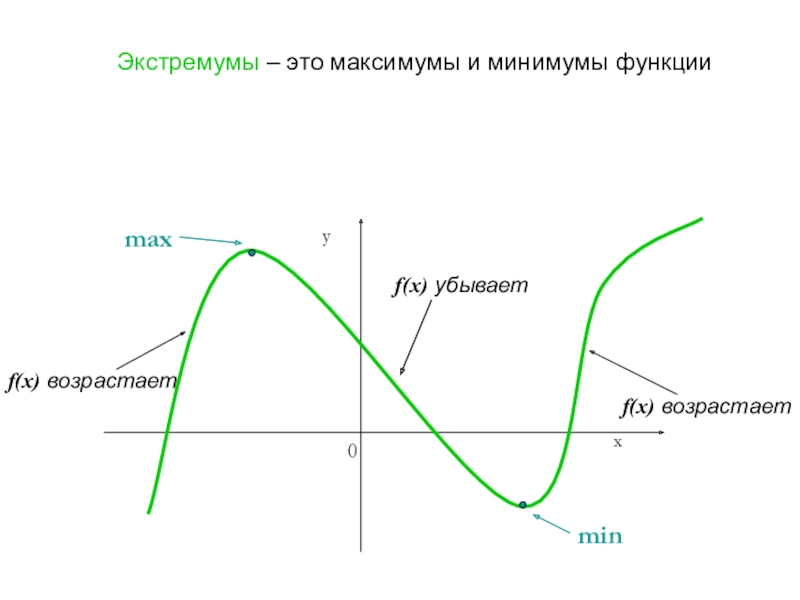
- 6. Экстремумы – это максимумы и минимумы функции maxminf(x) возрастаетf(x) убываетf(x) возрастает
- 7. https://resh.edu.ru/subject/lesson/3987/main/273814/Пройдите по ссылкам, посмотрите 2 фрагмента и вспомните материал первого курса.https://resh.edu.ru/subject/lesson/3966/start/201135/
- 8. Правило для нахождения промежутков монотонности функции:1.Найти первую
- 9. Правило для нахождения экстремумов функции: 1. Найти первую
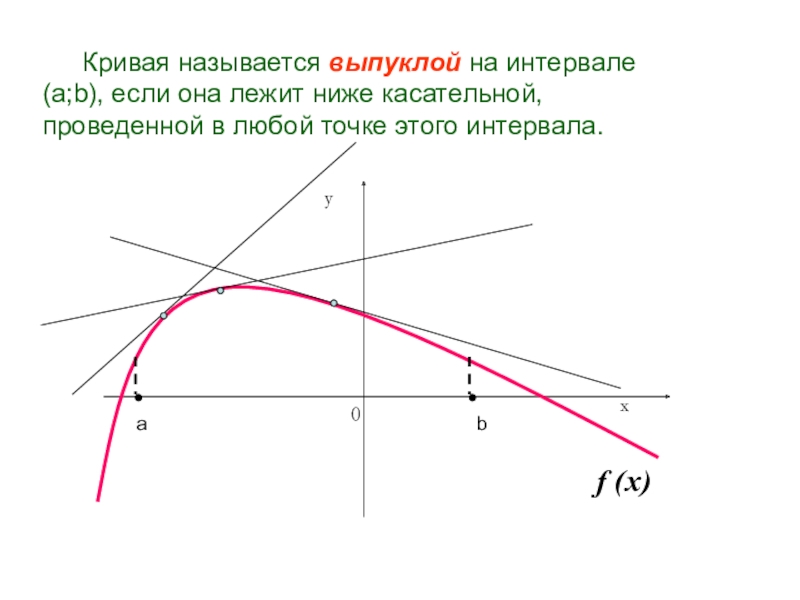
- 10. Кривая называется выпуклой на интервале (a;b), если
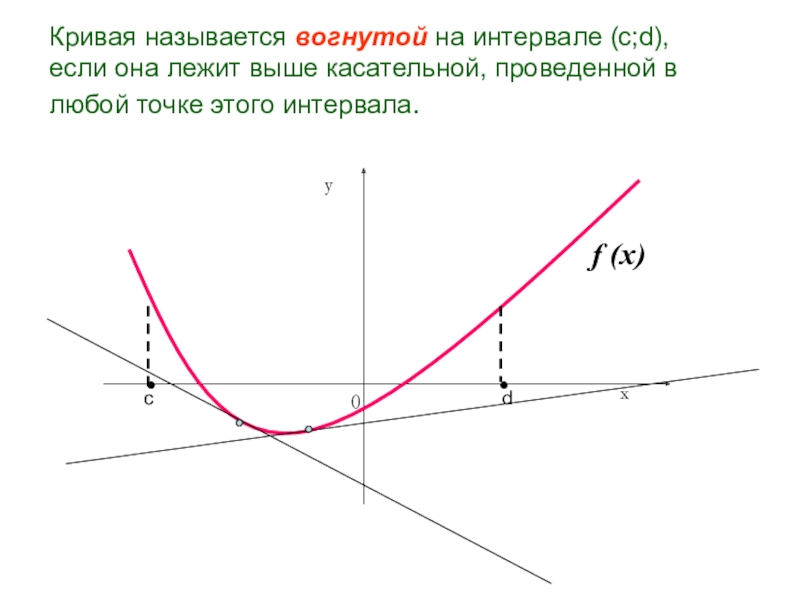
- 11. Кривая называется вогнутой на интервале (c;d), если
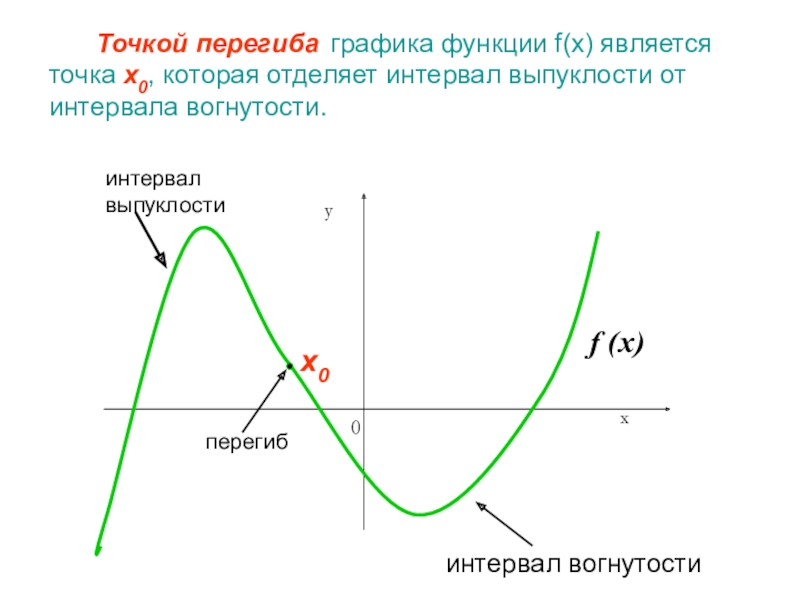
- 12. Точкой перегиба графика функции f(x) является
- 13. Признак выпуклости и вогнутости функцииЕсли
- 14. Правило нахождения интервалов выпуклости(вогнутости) и точек перегибаНайти
- 15. Общая схема исследования функции и построение ее
- 16. Скачать презентанцию
Чтобы построить график функции, необходимо исследовать ее свойства с помощью производной. Вспомним свойства функции, которые изучались на 1 курсе и добавим некоторые другие.
Слайды и текст этой презентации
Слайд 2Чтобы построить график функции, необходимо
исследовать ее свойства с помощью
производной.
добавим некоторые другие.Слайд 5 Интервалы монотонности функции – это интервалы возрастания или убывания функции
f(x)
возрастает
f(x) убывает
-1
Слайд 6Экстремумы – это максимумы и минимумы функции
max
min
f(x) возрастает
f(x) убывает
f(x)
возрастает
Слайд 7https://resh.edu.ru/subject/lesson/3987/main/273814/
Пройдите по ссылкам, посмотрите
2 фрагмента и вспомните
материал первого
курса.
https://resh.edu.ru/subject/lesson/3966/start/201135/
Слайд 8Правило для нахождения
промежутков монотонности функции:
1.Найти первую производную функции .
2.
Найти нули и точки разрыва .
3. На числовой прямой изобразить
нули первой производной.4. Определить знак в промежутках, на которые разбита область
определения точками из п.2
5. На интервале, где >0 – функция возрастает,
На интервале, где <0 – функция убывает.
Слайд 9Правило для нахождения экстремумов
функции:
1. Найти первую производную функции .
Найти
нули и точки разрыва . Это и есть точки,
подозрительные
на экстремум.3. На числовой прямой изобразить эти точки.
4. Определить знак в промежутках, на которые разбита область определения
точками из п.2
5. Если при переходе через точку экстремума знак производной
меняется с «+» на «- », то в данной точке max.
6. Если при переходе через точку экстремума знак производной
меняется с «-» на «+ », то в данной точке min.
Слайд 10 Кривая называется выпуклой на интервале (a;b), если она лежит ниже
касательной, проведенной в любой точке этого интервала.
f (x)
а
b
Слайд 11Кривая называется вогнутой на интервале (c;d), если она лежит выше
касательной, проведенной в любой точке этого интервала.
f (x)
с
d
Слайд 12 Точкой перегиба графика функции f(x) является точка x0, которая
отделяет интервал выпуклости от интервала вогнутости.
f (x)
x0
Слайд 13Признак выпуклости и вогнутости функции
Если
, то на этом интервале
функция выпукла.Если ,то на этом интервале функция вогнута
Признак точки перегиба:
если при переходе через точку x0 вторая производная меняет знак, то x0 является точкой перегиба.
Слайд 14Правило нахождения интервалов выпуклости(вогнутости) и точек перегиба
Найти область определения функции.
Найти
первую производную.
Найти вторую производную.
Найти критические точки - нули второй производной
и точки ее разрыва.Разбить область определения на промежутки. Определить знак f ’’(x) в полученных промежутках.
Записать интервалы выпуклости и вогнутости
Определить точки перегиба и найти значения функции в них.
Слайд 15Общая схема исследования функции и построение ее графика
1. Найти область
определения функции.
2. Периодичность функции
3. Четность/ нечетность функции
Функция является четной, если
выполняется условие: f(x)=f(-x), является нечетной, если выполняется условие f(-x)=-f(x),
4. Найти промежутки знакопостоянства функции.
Для этого найти нули функции . На числовой прямой обозначить полученные точки и найти знаки функции в каждом из полученных интервалов.
5. Найти промежутки монотонности функции (возрастание, убывание) с помощью первой производной.
6. Найти экстремумы функции (максимумы, минимумы)
7. Найти промежутки выпуклости и вогнутости графика функции с помощью второй производной
8. Найти точки перегиба графика.
9. Используя полученные данные, построить график функции.