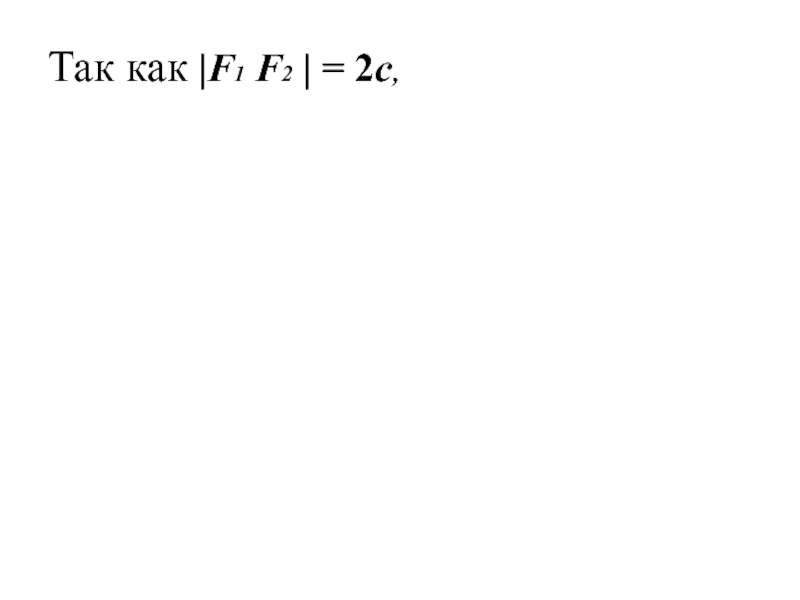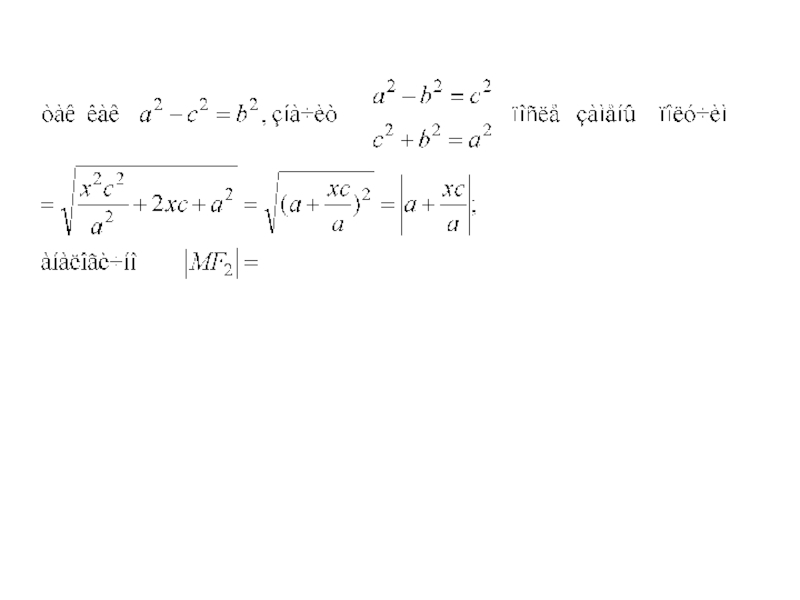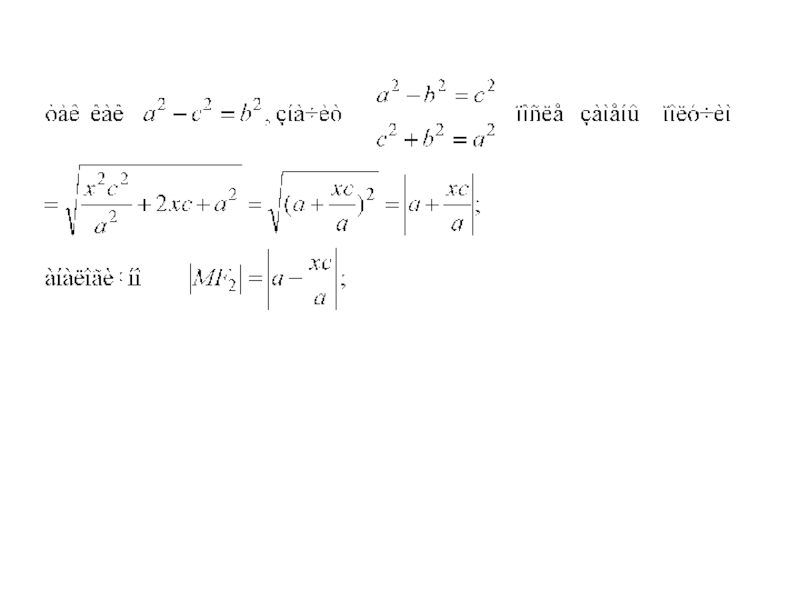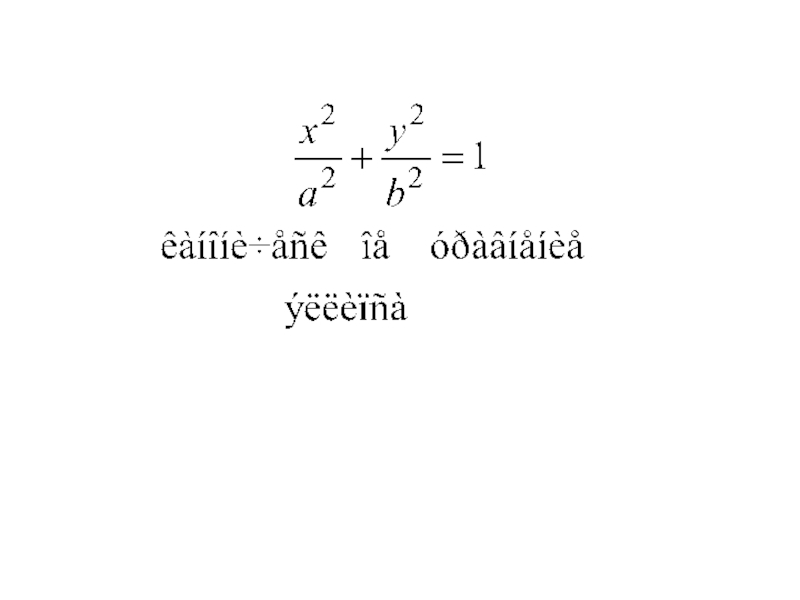Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Эллипс и его каноническое уравнение
Содержание
- 1. Эллипс и его каноническое уравнение
- 2. 1. Эллипс и его каноническое уравнение.
- 3. 1. Эллипс и его каноническое уравнение. Эллипсом
- 4. F1
- 5. F1 F2
- 6. F1 F2 M
- 7. F1 F2 M
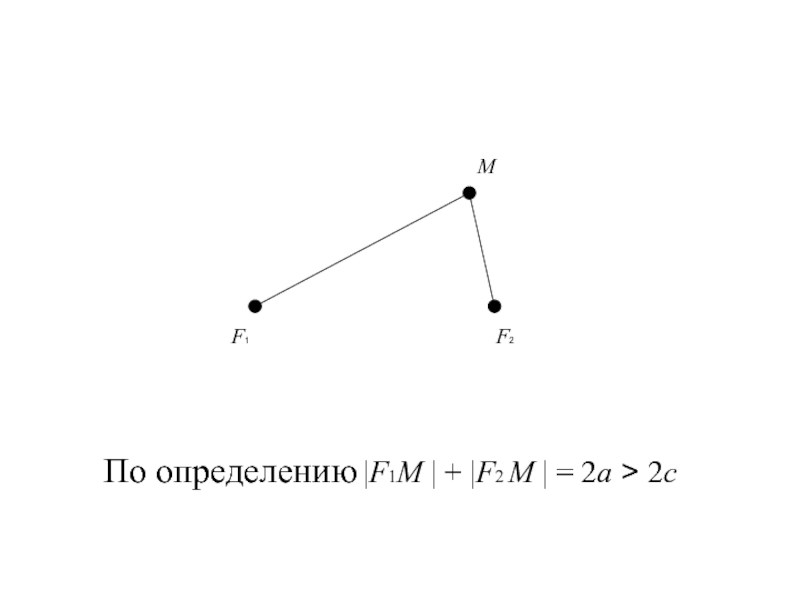
- 8. F1 F2 MПо определению |F1М | + |F2 М | = 2a > 2c
- 9. F1 F2 MПо определению |F1М | +
- 10. F1 F2 MДля вывода канонического уравнения эллипса
- 11. F1 F2 MДля вывода канонического уравнения эллипса
- 12. F1 F2 MДля вывода канонического уравнения эллипса
- 13. F1 F2 MОxДля вывода канонического уравнения эллипса
- 14. F1 F2 MОxyДля вывода канонического уравнения эллипса
- 15. Так как |F1 F2 | = 2c,
- 16. Так как |F1 F2 | = 2c,
- 17. Так как |F1 F2 | = 2c,
- 18. Так как |F1 F2 | = 2c,
- 19. Так как |F1 F2 | = 2c,
- 20. По определению |F1М | + |F2 М | = 2a (1)Получим
- 21. По определению |F1М | + |F2 М | = 2a (1) Получим
- 22. Слайд 22
- 23. Слайд 23
- 24. Таким образом, мы доказали, что координаты любой точки M (x; y) эллипса удовлетворяют уравнению (2).
- 25. Таким образом, мы доказали, что координаты любой
- 26. Если числа x и y удовлетворяют уравнению
- 27. Если числа x и y удовлетворяют уравнению
- 28. Докажем это утверждениеПусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Таким образом, уравнение (2) есть уравнение эллипса,
- 33. Слайд 33
- 34. 2. Исследование формы эллипса. Так как координаты
- 35. Следует, что для координат любой точки имеет
- 36. M(x,y)ОxyF2 F1
- 37. M(x,y)ОxyM1(x,-y)F2 F1
- 38. M(x,y)ОxyM2(-x,y)M1(x,-y)F2 F1
- 39. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)F2 F1
- 40. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=aF2 F1
- 41. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-aF2 F1
- 42. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=bF2 F1
- 43. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bF2 F1
- 44. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1F2 F1
- 45. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1A2F2 F1
- 46. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1B1A2F2 F1
- 47. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1B2B1A2F2 F1
- 48. F2 M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1B2B1A2F1
- 49. F2 MОxyА1B2B1A2F1
- 50. Точки пересечения эллипса с осями координат называются вершинами эллипса
- 51. Точки пересечения эллипса с осями координат называются
- 52. Точки пересечения эллипса с осями координат называются
- 53. Точки пересечения эллипса с осями координат называются
- 54. Отношение половины расстояния между фокусами эллипса (фокальное
- 55. Отношение половины расстояния между фокусами эллипса (фокальное
- 56. Отношение половины расстояния между фокусами эллипса (фокальное
- 57. 3.Директрисы эллипса.Две прямые перпендикулярные оси эллипса, на
- 58. 3.Директрисы эллипса.Две прямые перпендикулярные оси эллипса, на
- 59. F1 F2 MОxy
- 60. F1 F2 MОxyx=a/e
- 61. F1 F2 MОxyx=a/ex=-a/e
- 62. Теорема: Для того, чтобы точка лежала на
- 63. F1 F2 MОxyx=a/e
- 64. F1 F2 MОxyx=a/er2
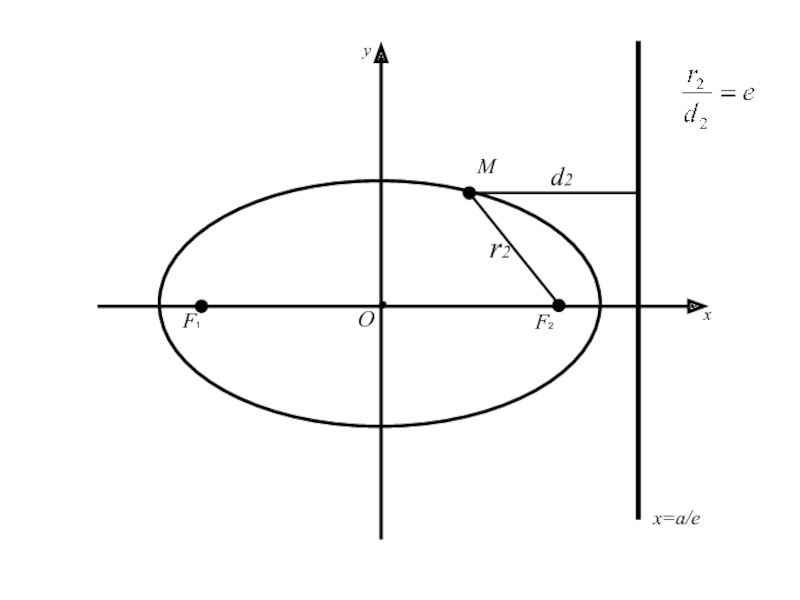
- 65. F1 F2 MОxyx=a/ed2r2
- 66. F1 F2 MОxyx=a/ed2r2
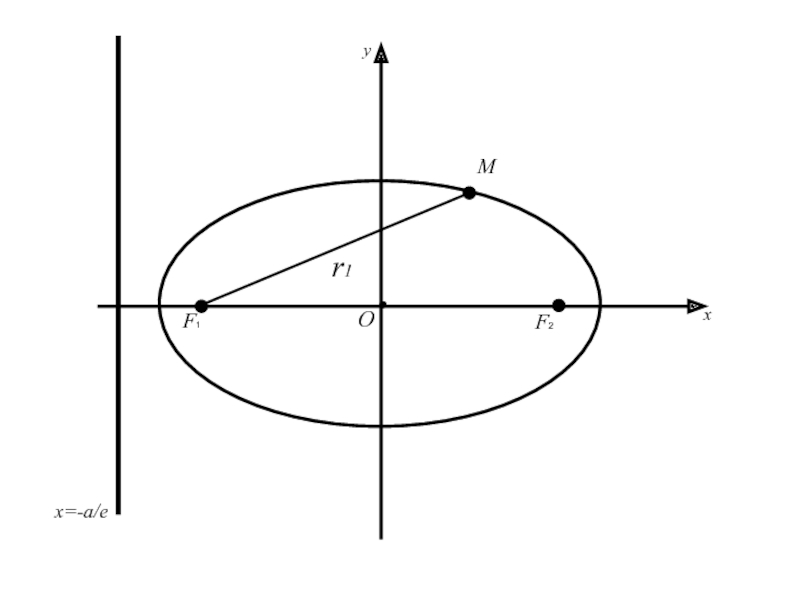
- 67. F1 F2 MОxyx=-a/e
- 68. F1 F2 MОxyx=-a/er1
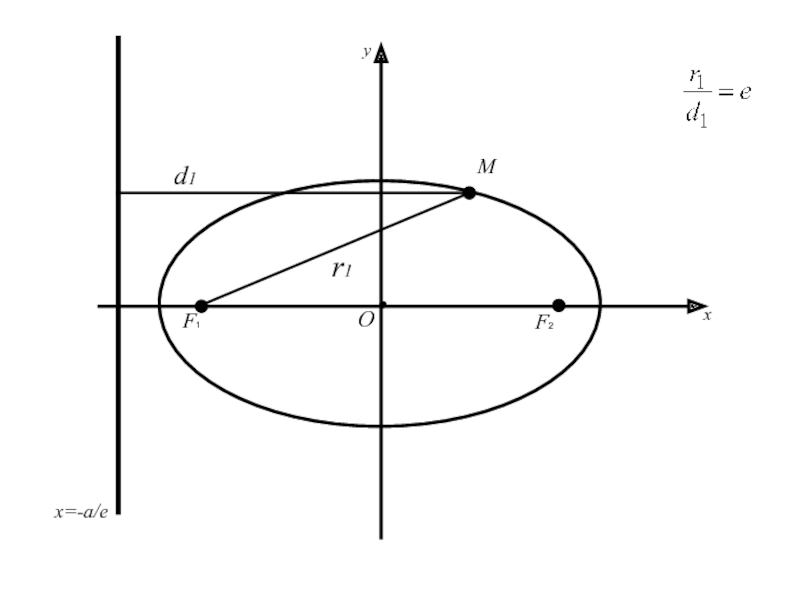
- 69. F1 F2 MОxyx=-a/ed1r1
- 70. F1 F2 MОxyx=-a/ed1r1
- 71. F1 F2 MОxyx=a/ed2r2
- 72. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется
- 73. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется
- 74. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что
- 75. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 76. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 77. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 78. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 79. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 80. Пусть существует точка
- 81. Пусть существует точка
- 82. Пусть существует точка
- 83. Пусть существует точка
- 84. Слайд 84
- 85. Слайд 85
- 86. Слайд 86
- 87. Скачать презентанцию
1. Эллипс и его каноническое уравнение.
Слайды и текст этой презентации
Слайд 10
F1
F2
M
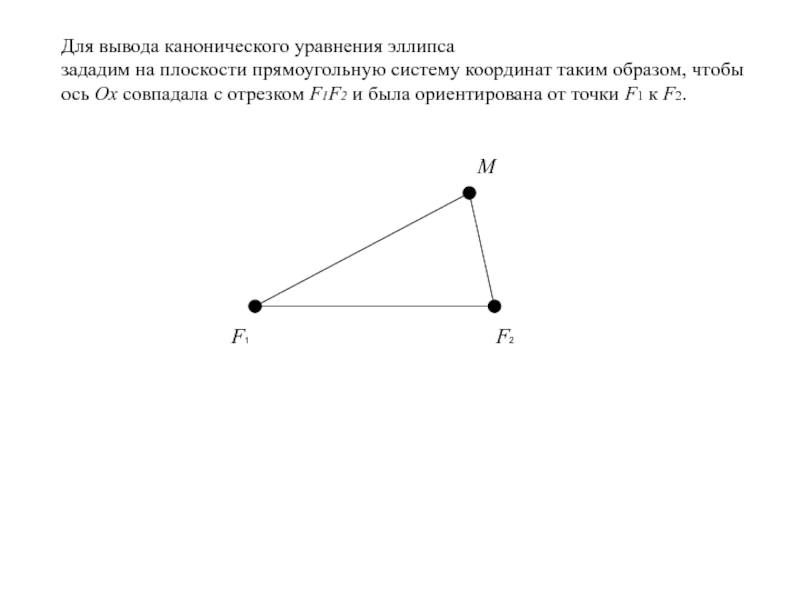
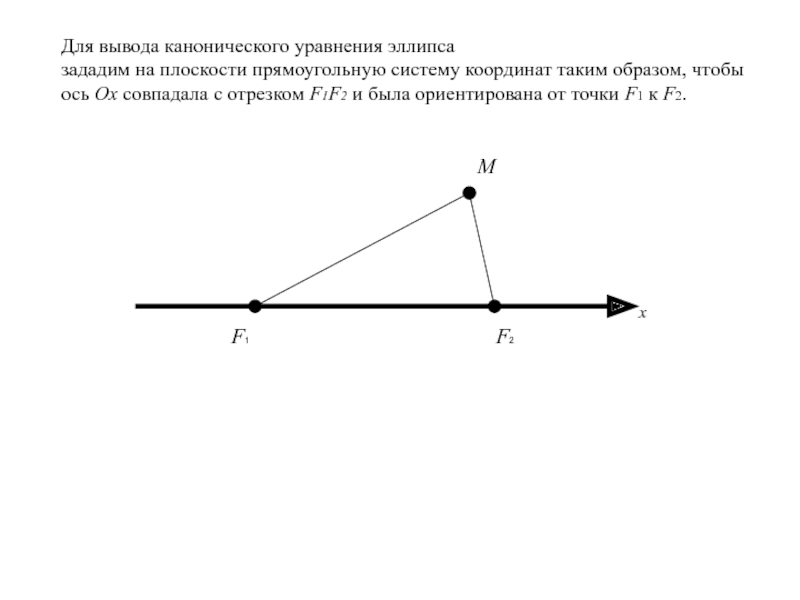
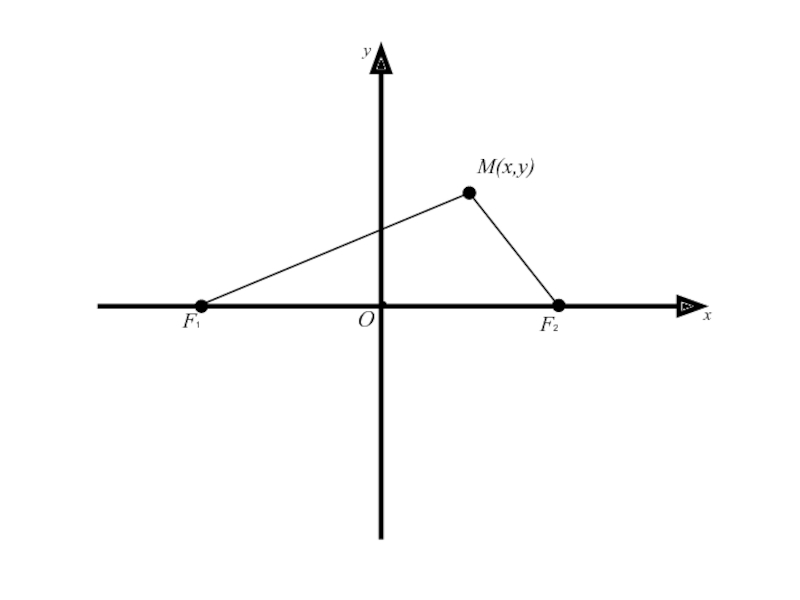
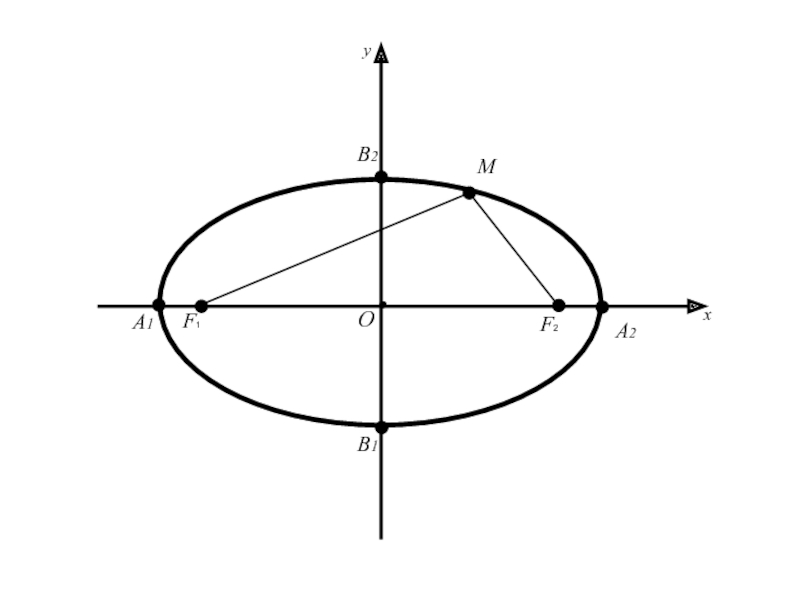
Для вывода канонического уравнения эллипса
зададим на плоскости
прямоугольную систему координат таким образом, чтобы ось Ox совпадала с
отрезком F1F2 и была ориентирована от точки F1 к F2.Слайд 11
F1
F2
M
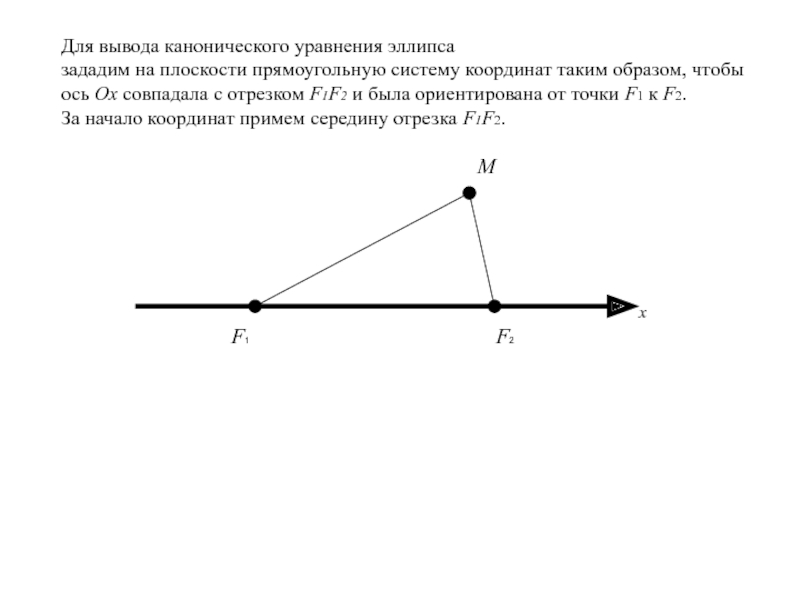
Для вывода канонического уравнения эллипса
зададим на плоскости
прямоугольную систему координат таким образом, чтобы ось Ox совпадала с
отрезком F1F2 и была ориентирована от точки F1 к F2.x
Слайд 12
F1
F2
M
Для вывода канонического уравнения эллипса
зададим на плоскости
прямоугольную систему координат таким образом, чтобы ось Ox совпадала с
отрезком F1F2 и была ориентирована от точки F1 к F2.За начало координат примем середину отрезка F1F2.
x
Слайд 13
F1
F2
M
О
x
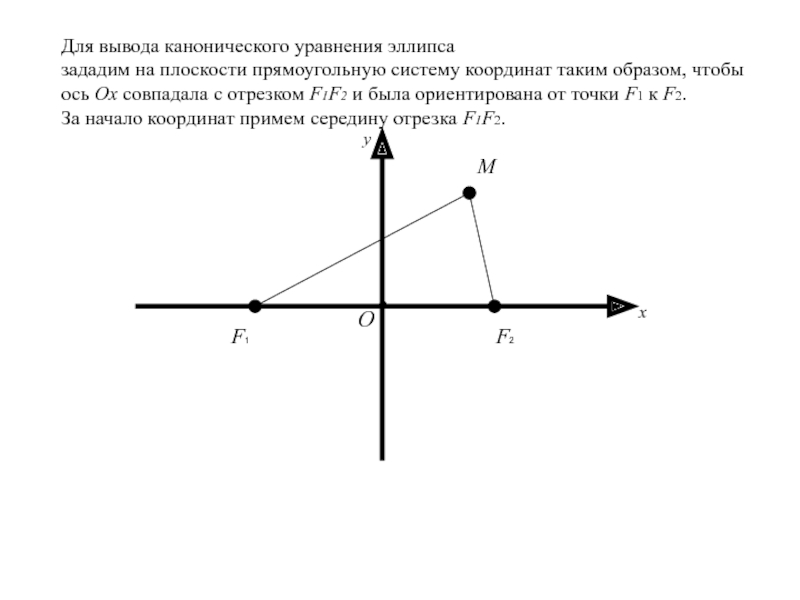
Для вывода канонического уравнения эллипса
зададим на плоскости
прямоугольную систему координат таким образом, чтобы ось Ox совпадала с
отрезком F1F2 и была ориентирована от точки F1 к F2.За начало координат примем середину отрезка F1F2.
Слайд 14
F1
F2
M
О
x
y
Для вывода канонического уравнения эллипса
зададим на плоскости
прямоугольную систему координат таким образом, чтобы ось Ox совпадала с
отрезком F1F2 и была ориентирована от точки F1 к F2.За начало координат примем середину отрезка F1F2.
Слайд 17Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
Слайд 18Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогдаСлайд 19Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогда
Слайд 24
Таким образом, мы доказали, что координаты любой точки M (x;
y) эллипса удовлетворяют уравнению (2).
Слайд 25
Таким образом, мы доказали, что координаты любой точки M (x;
y) эллипса удовлетворяют уравнению (2). Однако это уравнение пока нельзя
назвать уравнением эллипса, т.к. не доказано обратное предположение:Слайд 26Если числа x и y удовлетворяют уравнению (2), то точка
M (x; y) удовлетворяет соотношению (1), т.е. лежит на эллипсе.
Слайд 27Если числа x и y удовлетворяют уравнению (2), то точка
M (x; y) удовлетворяет соотношению (1), т.е. лежит на эллипсе.
Слайд 32Таким образом, уравнение (2) есть уравнение эллипса, т.к. доказано, что
координаты любой точки M (x; y) эллипса, т.е. любой точки,
для которой выполняется выражение (1) удовлетворяет уравнению (2) и обратно, если два числа x и y удовлетворяет уравнению (2), то точка M (x; y) удовлетворяет соотношению (1), т.е. лежит на эллипсе.Слайд 342. Исследование формы эллипса.
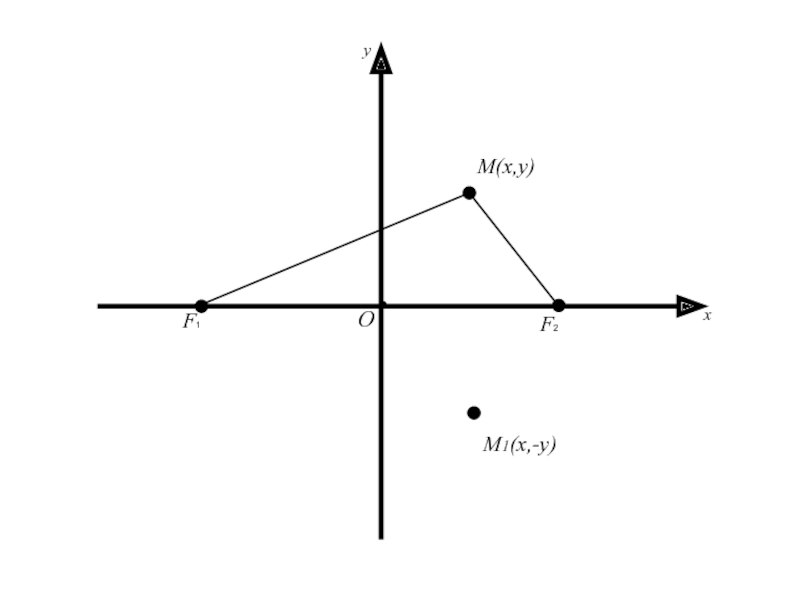
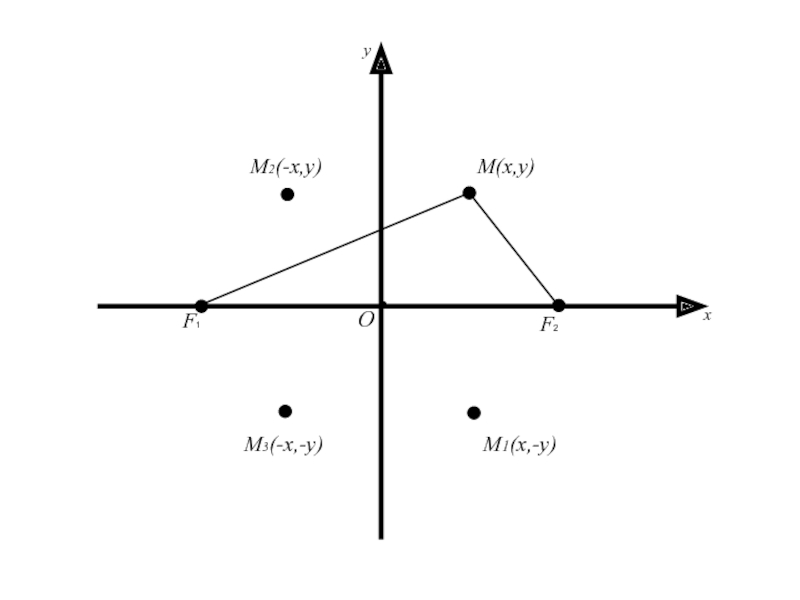
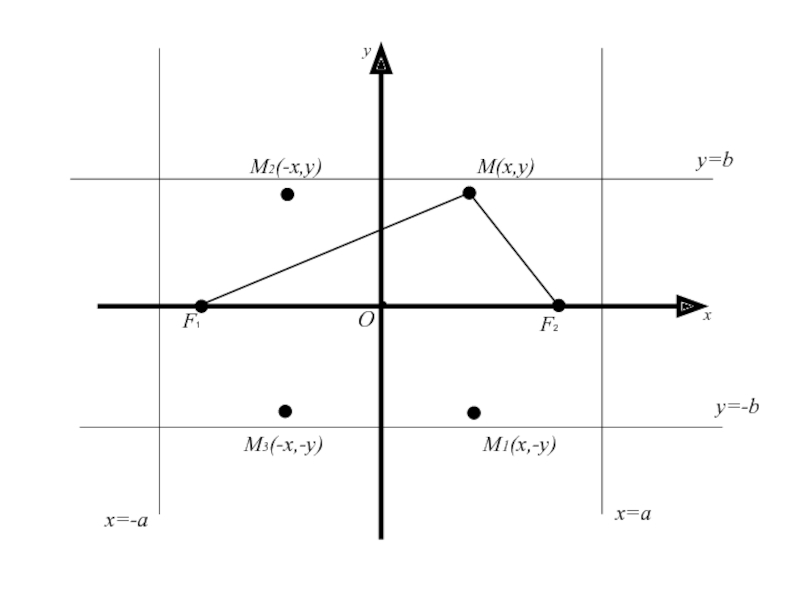
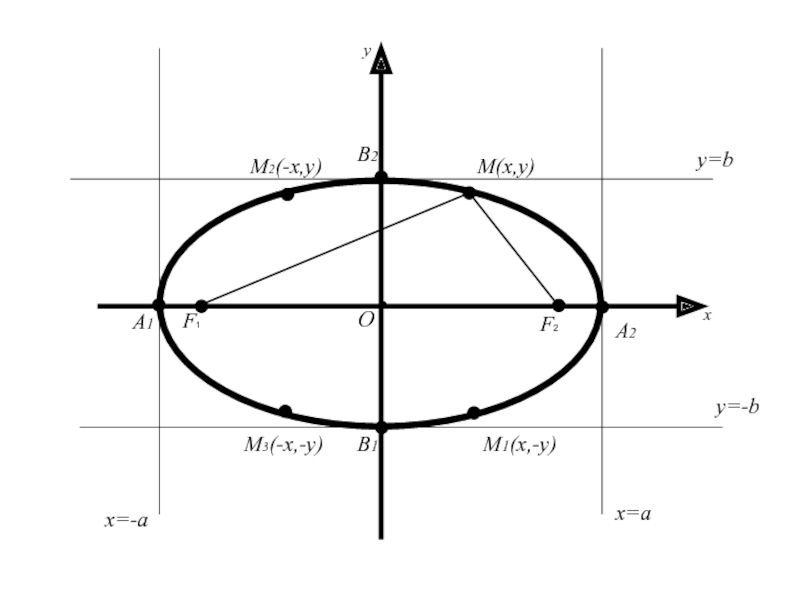
Так как координаты x и y
входят в уравнение в четной степени, то если на эллипсе
лежит любая точка M(x, y) ( т.е. координаты этой точки удовлетворяют уравнению(2)), то на этом эллипсе будут лежать точки M1(-x,y) и M2(x, -y), симметричные с точкой M(x, y) относительно осей Ox и Oy и точка M3(-x;-y), cимметричная относительно начала координат.Следовательно, оси Ox и Oy являются осями симметрии, а начало координат – центром симметрии эллипса.
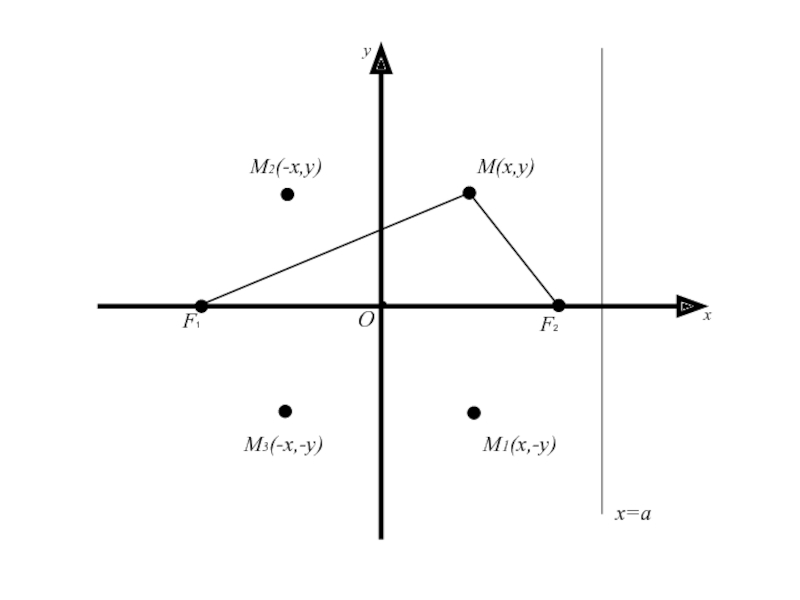
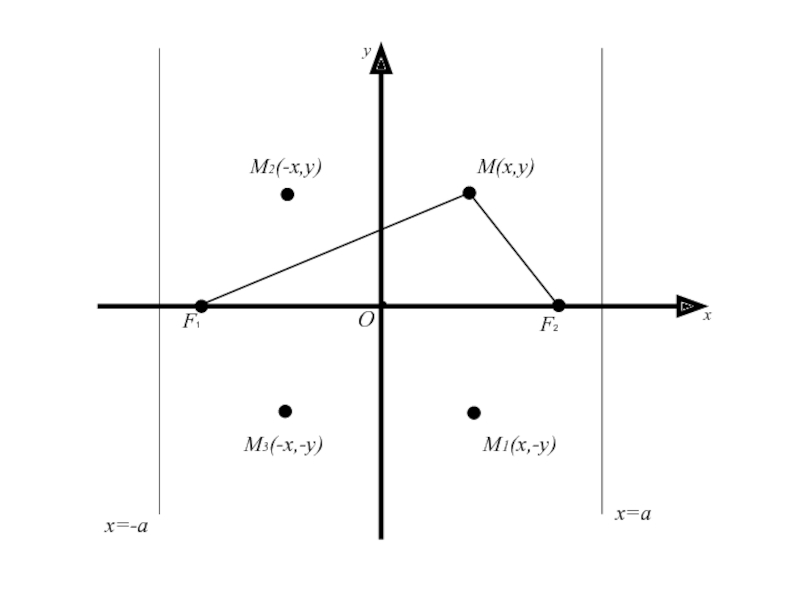
Слайд 35Следует, что для координат любой точки имеет место
Геометрически это
означает, что эллипс расположен внутри прямоугольника, сторонами которого являются прямые
x=a, x=-a, y=b, y=-b
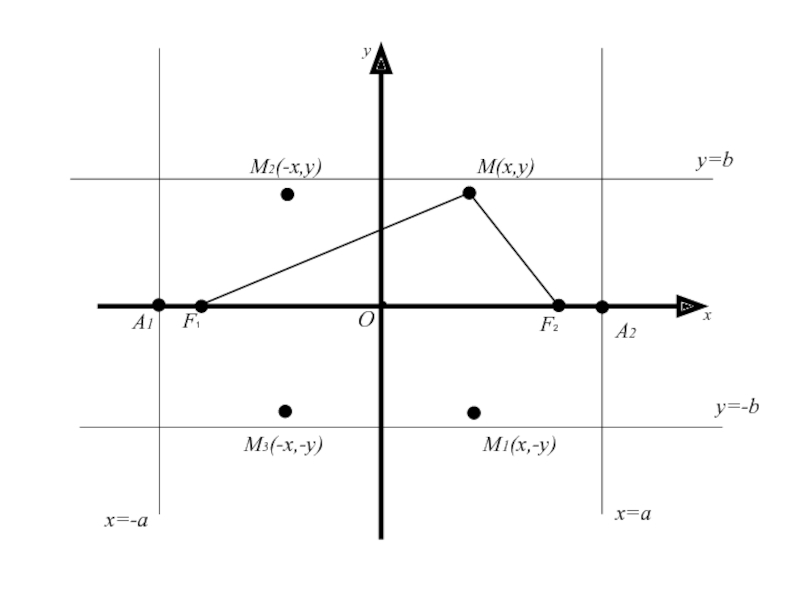
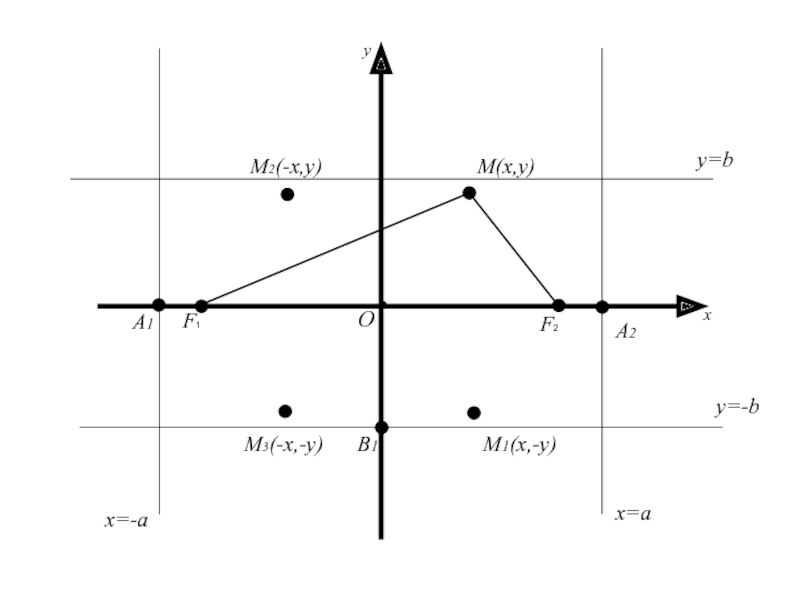
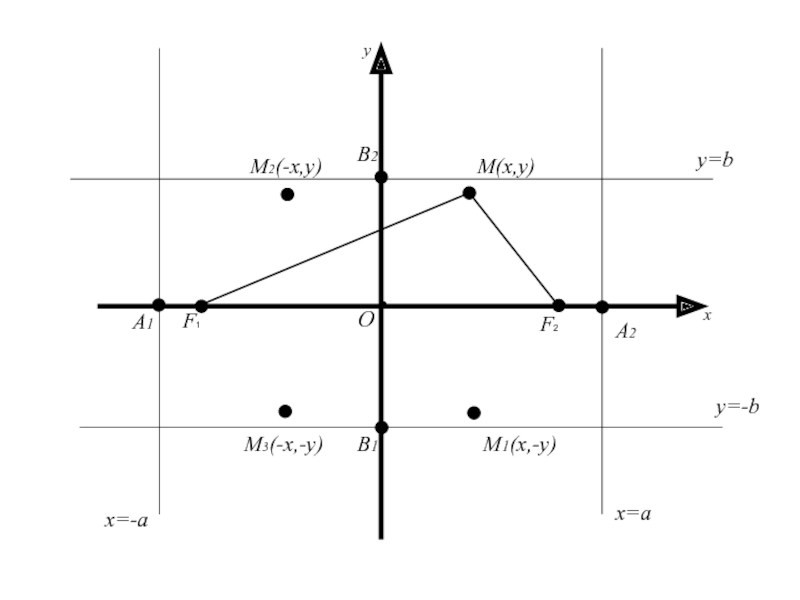
Слайд 51Точки пересечения эллипса с осями координат называются вершинами эллипса
Полуосью
эллипса называется отрезок, одним концом которого является центр симметрии эллипса,
а другим одна из его вершин.Слайд 52Точки пересечения эллипса с осями координат называются вершинами эллипса
Полуосью
эллипса называется отрезок, одним концом которого является центр симметрии эллипса,
а другим одна из его вершин.Будем предполагать, что в каноническом уравнении (2) a>b, тогда
a – большая полуось
b – меньшая полуось
Слайд 53Точки пересечения эллипса с осями координат называются вершинами эллипса
Полуосью
эллипса называется отрезок, одним концом которого является центр симметрии эллипса,
а другим одна из его вершин.Будем предполагать, что в каноническом уравнении (2) a>b, тогда
a – большая полуось
b – меньшая полуось
В случае a=b уравнение (2) примет вид
Слайд 54Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей
полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:
Слайд 55Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей
полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:
Слайд 56Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей
полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:
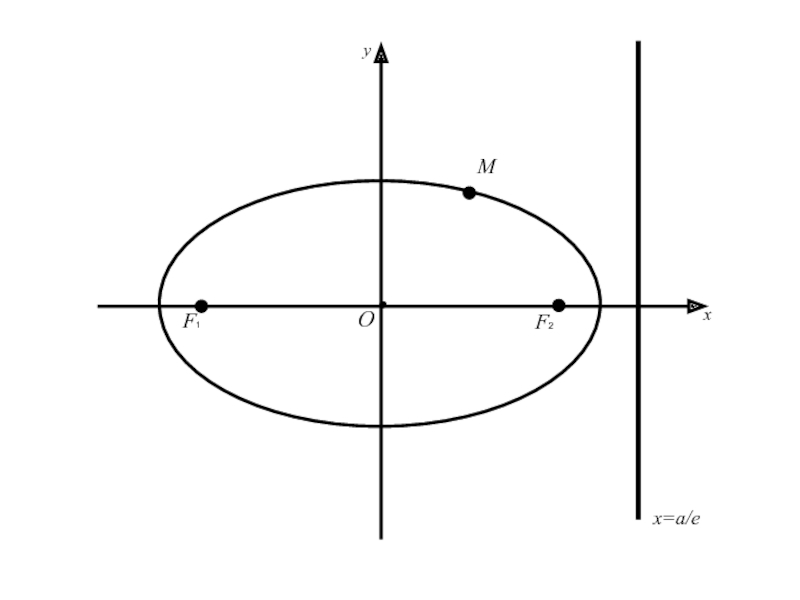
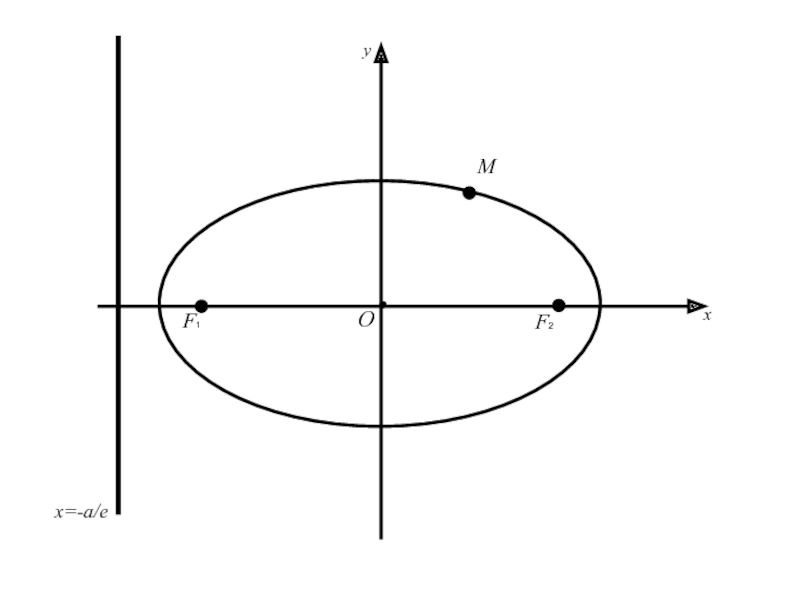
Слайд 573.Директрисы эллипса.
Две прямые перпендикулярные оси эллипса, на которой расположены его
фокусы, и отстоящие от центра эллипса на расстояние a/e, где
a –большая полуось эллипса, e –эксцентриситет называются директрисами эллипса.
Слайд 583.Директрисы эллипса.
Две прямые перпендикулярные оси эллипса, на которой расположены его
фокусы, и отстоящие от центра эллипса на расстояние a/e, где
a –большая полуось эллипса, e –эксцентриситет называются директрисами эллипса.Уравнения директрис имеют вид
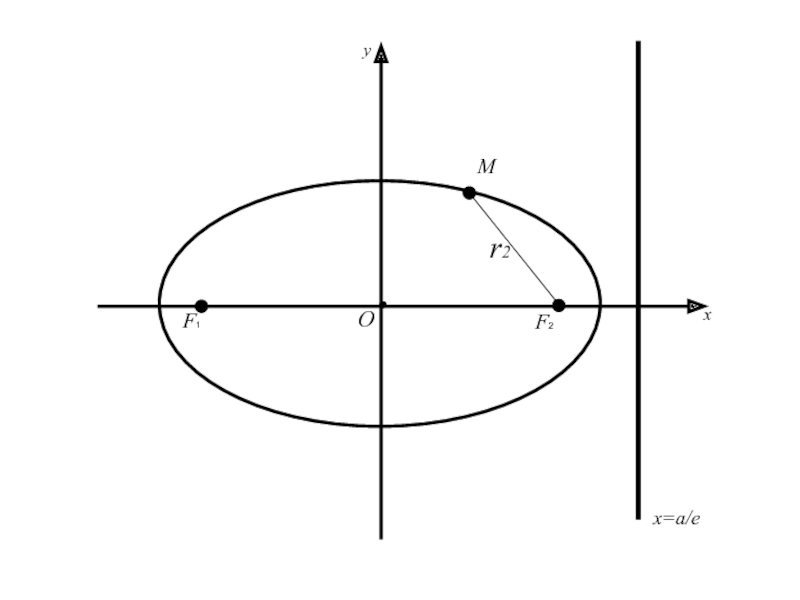
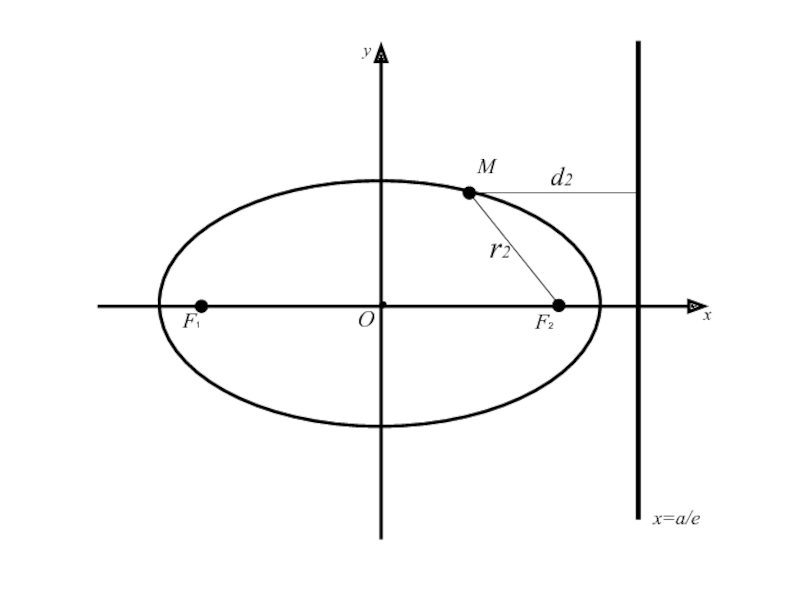
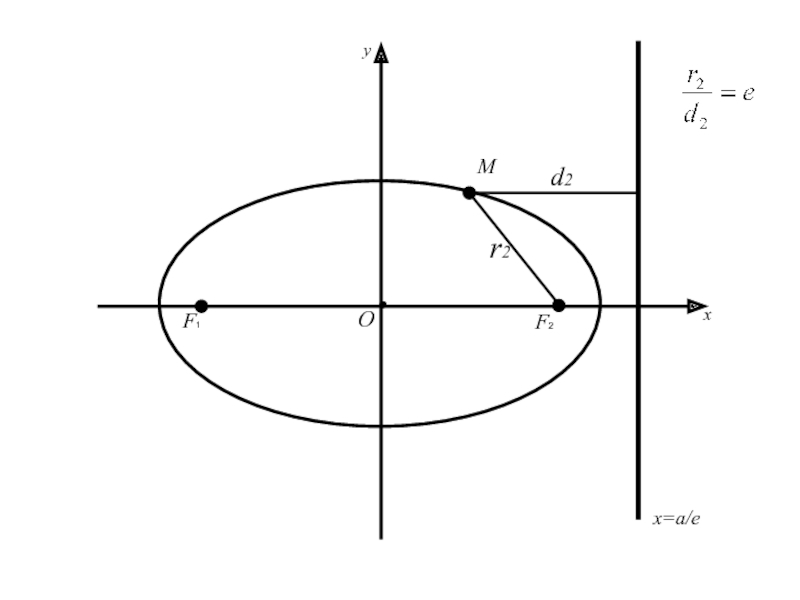
Слайд 62Теорема: Для того, чтобы точка лежала на эллипсе необходимо и достаточно,
чтобы отношение расстояния от этой точки до фокуса эллипса к
расстоянию от той же точки до директрисы, соответствующей рассматриваемому фокусу, было равно эксцентриситету эллипса.Слайд 74 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
Слайд 75 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 76 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 77 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 78 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 79 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 80 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)(<=)
Слайд 81 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
(<=)
Слайд 82 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
(<=)
Слайд 83 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
(<=)