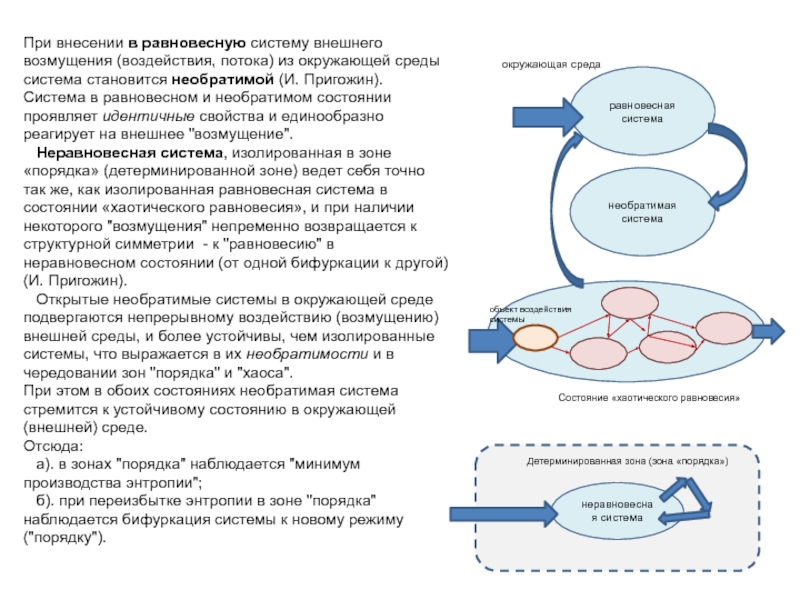
Слайд 2При внесении в равновесную систему внешнего возмущения (воздействия, потока) из
окружающей среды система становится необратимой (И. Пригожин).
Система в равновесном и
необратимом состоянии проявляет идентичные свойства и единообразно реагирует на внешнее "возмущение".
Неравновесная система, изолированная в зоне «порядка» (детерминированной зоне) ведет себя точно так же, как изолированная равновесная система в состоянии «хаотического равновесия», и при наличии некоторого "возмущения" непременно возвращается к структурной симметрии - к "равновесию" в неравновесном состоянии (от одной бифуркации к другой) (И. Пригожин).
Открытые необратимые системы в окружающей среде подвергаются непрерывному воздействию (возмущению) внешней среды, и более устойчивы, чем изолированные системы, что выражается в их необратимости и в чередовании зон "порядка" и "хаоса".
При этом в обоих состояниях необратимая система стремится к устойчивому состоянию в окружающей (внешней) среде.
Отсюда:
а). в зонах "порядка" наблюдается "минимум производства энтропии";
б). при переизбытке энтропии в зоне "порядка" наблюдается бифуркация системы к новому режиму ("порядку").
Слайд 3Энтропия в замкнутой системе непрестанно возрастает до тех пор, пока
не достигает своего максимального значения в состоянии термодинамического равновесия.
Процесс эволюции
равновесной системы
В приращении энтропии dS участвуют две ее составляющие:
deS - перенос энтропии через границы системы (в окружающую среду или в пределы другой системы);
diS – величина энтропии, произведенной в системе.
Согласно второму началу термодинамики, производство энтропии внутри рабочей системы положительно:
dS=deS+diS, при diS>0
Данная формула применяется для расчета энергетических затрат и потерь при работе систем, связанных с тепловыми машинами и показывает: какое количество энергии или вещества в единицу времени надо затрачивать, чтобы поддерживать систему в рабочем состоянии с учетом выполняемой работы - А за вычетом бесполезных потерь - deS, расходуемых на теплообмен системы с внешней средой, и пригодна лишь для работы механических систем: при прекращении подачи энергии система возвращается в первоначальное, термодинамическое равновесие с внешней средой и формула второго начала термодинамики принимает вид:
dS=0 при diS = 0 и deS = 0
т.е. без постоянной "подпитки" энергией извне механические системы прекращают работу.

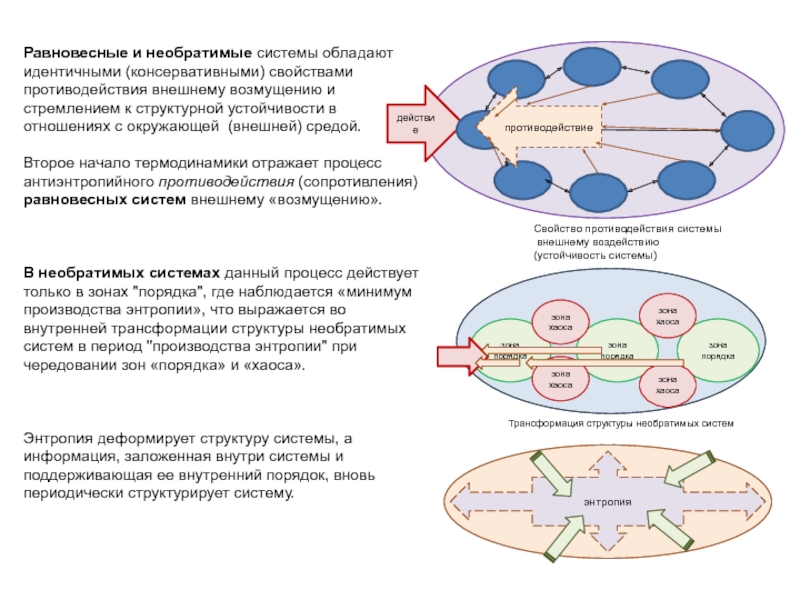
Слайд 4Равновесные и необратимые системы обладают идентичными (консервативными) свойствами противодействия внешнему
возмущению и стремлением к структурной устойчивости в отношениях с окружающей
(внешней) средой.
Второе начало термодинамики отражает процесс антиэнтропийного противодействия (сопротивления) равновесных систем внешнему «возмущению».
В необратимых системах данный процесс действует только в зонах "порядка", где наблюдается «минимум производства энтропии», что выражается во внутренней трансформации структуры необратимых систем в период "производства энтропии" при чередовании зон «порядка» и «хаоса».
Энтропия деформирует структуру системы, а информация, заложенная внутри системы и поддерживающая ее внутренний порядок, вновь периодически структурирует систему.
Слайд 5Внешние воздействия на систему (1) провоцируют активизацию корпоративного поведения частиц в
изолированной механической системе (2), и система после совершения работы (или
после расконсервации) избавляется от избыточной энергии (3) (активности частиц), возвращаясь в первоначальное состояние.
Таким образом происходит процесс противодействия (сопротивления) систем внешнему "возмущению", при котором системы совершают волевой откат в «хаотическое равновесие» (состояние возбужденной структурной симметрии "возмущенной" системы).
В период первичного процесса выполнения работы системой в результате внешнего воздействия определяющими оказываются свойства термодинамической системы, которые отражают:
- поведение изолированной системы, как активного субъекта, совершающего работу;
- конфликтные субъект - объектные отношения между изолированной системой и внешним раздражителем, предварительно "накачавшим" систему.
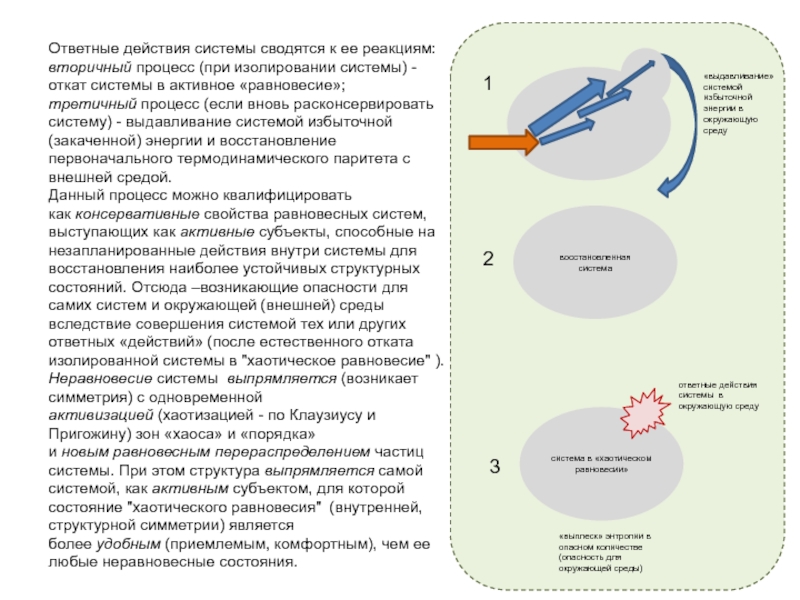
Слайд 6Ответные действия системы сводятся к ее реакциям:
вторичный процесс (при изолировании системы)
- откат системы в активное «равновесие»;
третичный процесс (если вновь расконсервировать систему)
- выдавливание системой избыточной (закаченной) энергии и восстановление первоначального термодинамического паритета с внешней средой.
Данный процесс можно квалифицировать как консервативные свойства равновесных систем, выступающих как активные субъекты, способные на незапланированные действия внутри системы для восстановления наиболее устойчивых структурных состояний. Отсюда –возникающие опасности для самих систем и окружающей (внешней) среды вследствие совершения системой тех или других ответных «действий» (после естественного отката изолированной системы в "хаотическое равновесие" ).
Неравновесие системы выпрямляется (возникает симметрия) с одновременной активизацией (хаотизацией - по Клаузиусу и Пригожину) зон «хаоса» и «порядка» и новым равновесным перераспределением частиц системы. При этом структура выпрямляется самой системой, как активным субъектом, для которой состояние "хаотического равновесия" (внутренней, структурной симметрии) является более удобным (приемлемым, комфортным), чем ее любые неравновесные состояния.
«выдавливание» системой избыточной энергии в окружающую среду
восстановленная система
система в «хаотическом равновесии»
ответные действия системы в окружающую среду
«выплеск» энтропии в опасном количестве (опасность для окружающей среды)
1
2
3
Слайд 7В системе происходят деструктивно - репродуктивные процессы, выражающиеся во внутренних
переходах и взаимодействиях:
- «производство энтропии»;
- «рационализация»
системы (стремление системы самовосстановиться).
В этот период в системе происходят два вида (порядка) процессов:
1. Стремление к внутренней, структурной устойчивости (симметрии) - противодействие (сопротивление) системы деструктивному процессу возрастания энтропии и возникновению деструктивных асимметрий и деформаций:
- в изолированных системах – выражается в возвращении к "хаотическому равновесию" (к структурной симметрии);
- в необратимых системах – в зонах «хаоса» наблюдается рост (производство) энтропии, а в зонах "порядка" процесс стремления к устойчивости отражается в "минимуме производства энтропии", а при перепроизводстве энтропии - в бифуркациях к новым симметричным "порядкам".
2. Сохранение в зонах "порядка" структурной "гибкости" и при необходимости самосохранения - переход к новым начальным условиям равновесия (симметрии), режиму функционирования и типу структуры.
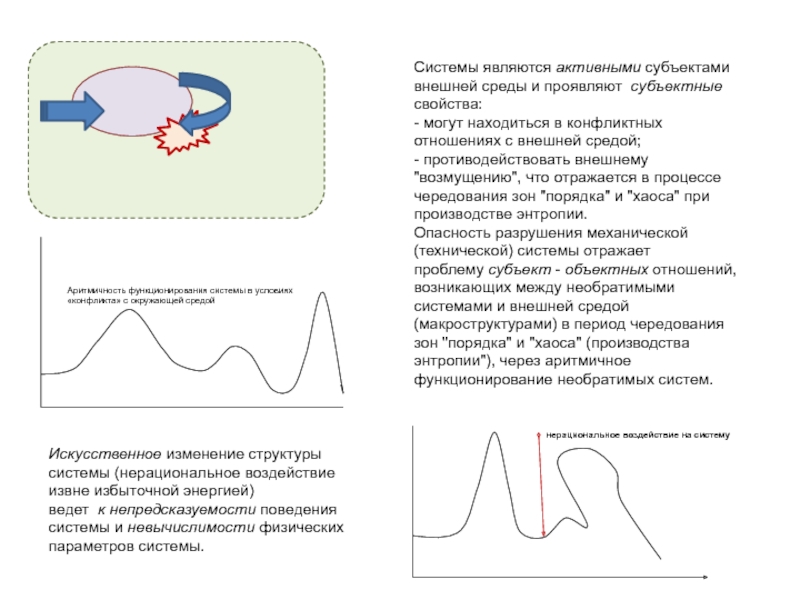
Слайд 8Искусственное изменение структуры системы (нерациональное воздействие извне избыточной энергией) ведет к непредсказуемости поведения
системы и невычислимости физических параметров системы.
Системы являются активными субъектами внешней среды и проявляют
субъектные свойства:
- могут находиться в конфликтных отношениях с внешней средой;
- противодействовать внешнему "возмущению", что отражается в процессе чередования зон "порядка" и "хаоса" при производстве энтропии.
Опасность разрушения механической (технической) системы отражает проблему субъект - объектных отношений, возникающих между необратимыми системами и внешней средой (макроструктурами) в период чередования зон "порядка" и "хаоса" (производства энтропии"), через аритмичное функционирование необратимых систем.
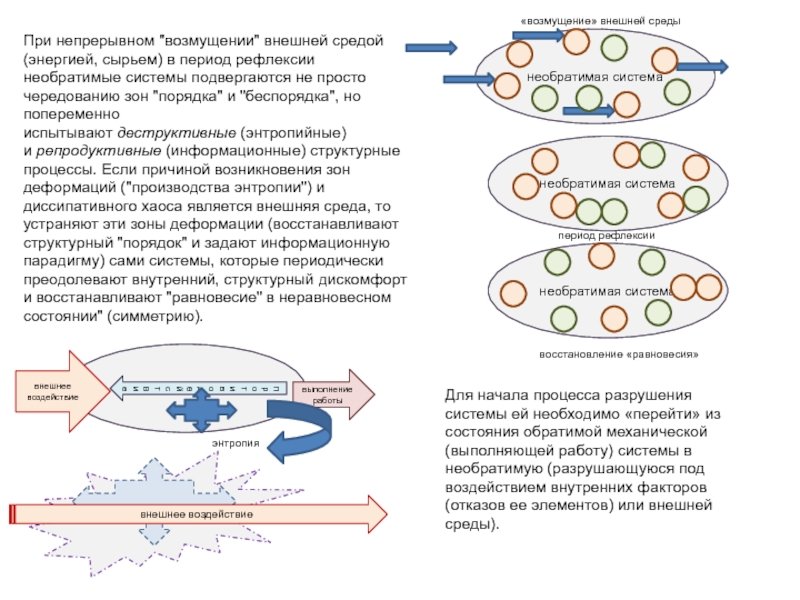
Слайд 9При непрерывном "возмущении" внешней средой (энергией, сырьем) в период рефлексии
необратимые системы подвергаются не просто чередованию зон "порядка" и "беспорядка",
но попеременно испытывают деструктивные (энтропийные) и репродуктивные (информационные) структурные процессы. Если причиной возникновения зон деформаций ("производства энтропии") и диссипативного хаоса является внешняя среда, то устраняют эти зоны деформации (восстанавливают структурный "порядок" и задают информационную парадигму) сами системы, которые периодически преодолевают внутренний, структурный дискомфорт и восстанавливают "равновесие" в неравновесном состоянии" (симметрию).
Для начала процесса разрушения системы ей необходимо «перейти» из состояния обратимой механической (выполняющей работу) системы в необратимую (разрушающуюся под воздействием внутренних факторов (отказов ее элементов) или внешней среды).
Слайд 10Бифуркация - катастрофический скачок, конфликтный срыв, узел взаимодействия между случаем и
внешним ограничением, между колебаниями и необратимостью.
"Бифуркация - это проявление внутренней
дифференциации между частями самой системы и системой и окружающей средой« (И. Пригожин).
Бифурка́ция — термин происходит от лат. bifurcus — «раздвоенный» и употребляется в широком смысле для обозначения всевозможных качественных перестроек или метаморфоз различных объектов при изменении параметров, от которых они зависят.
Точка бифуркации - смена установившегося режима работы системы. (Википедия).
Флуктуация (от лат. fluctuatio — колебание) — термин, характеризующий любое колебание или любое периодическое изменение. В квантовой механике — случайные отклонения от среднего значения физических величин, характеризующих систему из большого числа частиц; вызываются тепловым движением частиц или квантовомеханическими эффектами.
Бифуркация такого типа называется бифуркацией типа вил. Физический смысл этого явления понятен из того, что силу -(а*x+b*x*x*x) можно описать с помощью потенциальной энергии.
Когда а становится отрицательным, потенциал с одной ямой заменяется потенциалом с двумя ямами. При этом происходит качественное изменение динамики системы, и поэтому а=0 является критическим бифуркационным значением.
Бифуркационная диаграмма:
бифуркация типа вил, отвечающая переходу из состояния с одним устойчивым положением равновесия в состояние с двумя устойчивыми равновесными точками, где по мере изменения некоторого управляющего параметра пара комплексно-сопряженных собственных значений s1=i*w+q, s2=-i*w+q переходит из левой части плоскости (q<0, устойчивая спираль) в правую часть (q>0, неустойчивая спираль) и возникает периодическое движение, называемое предельным циклом.

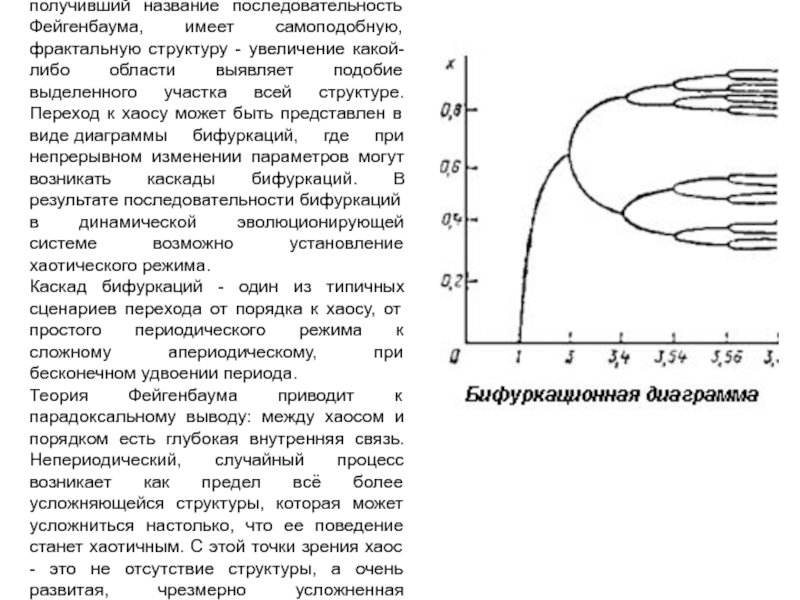
Слайд 11Необычайно простой путь к хаосу, получивший название последовательность Фейгенбаума, имеет
самоподобную, фрактальную структуру - увеличение какой-либо области выявляет подобие выделенного
участка всей структуре. Переход к хаосу может быть представлен в виде диаграммы бифуркаций, где при непрерывном изменении параметров могут возникать каскады бифуркаций. В результате последовательности бифуркаций в динамической эволюционирующей системе возможно установление хаотического режима.
Каскад бифуркаций - один из типичных сценариев перехода от порядка к хаосу, от простого периодического режима к сложному апериодическому, при бесконечном удвоении периода.
Теория Фейгенбаума приводит к парадоксальному выводу: между хаосом и порядком есть глубокая внутренняя связь. Непериодический, случайный процесс возникает как предел всё более усложняющейся структуры, которая может усложниться настолько, что ее поведение станет хаотичным. С этой точки зрения хаос - это не отсутствие структуры, а очень развитая, чрезмерно усложненная структура.
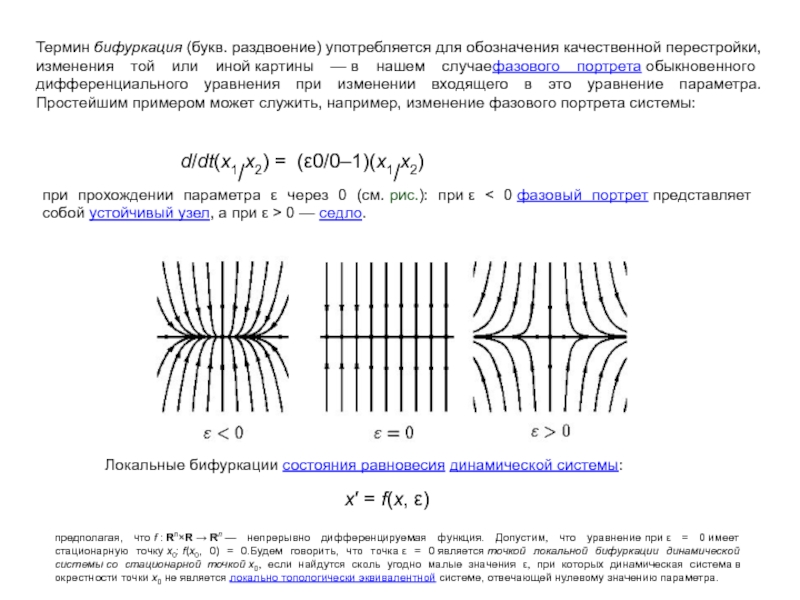
Слайд 12Термин бифуркация (букв. раздвоение) употребляется для обозначения качественной перестройки, изменения той или
иной картины — в нашем случаефазового портрета обыкновенного дифференциального уравнения при изменении входящего
в это уравнение параметра. Простейшим примером может служить, например, изменение фазового портрета системы:
d/dt(x1/x2) = (ε0/0–1)(x1/x2)
при прохождении параметра ε через 0 (см. рис.): при ε < 0 фазовый портрет представляет собой устойчивый узел, а при ε > 0 — седло.
x′ = f(x, ε)
Локальные бифуркации состояния равновесия динамической системы:
предполагая, что f : Rn×R → Rn — непрерывно дифференцируемая функция. Допустим, что уравнение при ε = 0 имеет стационарную точку x0: f(x0, 0) = 0.Будем говорить, что точка ε = 0 является точкой локальной бифуркации динамической системы со стационарной точкой x0, если найдутся сколь угодно малые значения ε, при которых динамическая система в окрестности точки x0 не является локально топологически эквивалентной системе, отвечающей нулевому значению параметра.
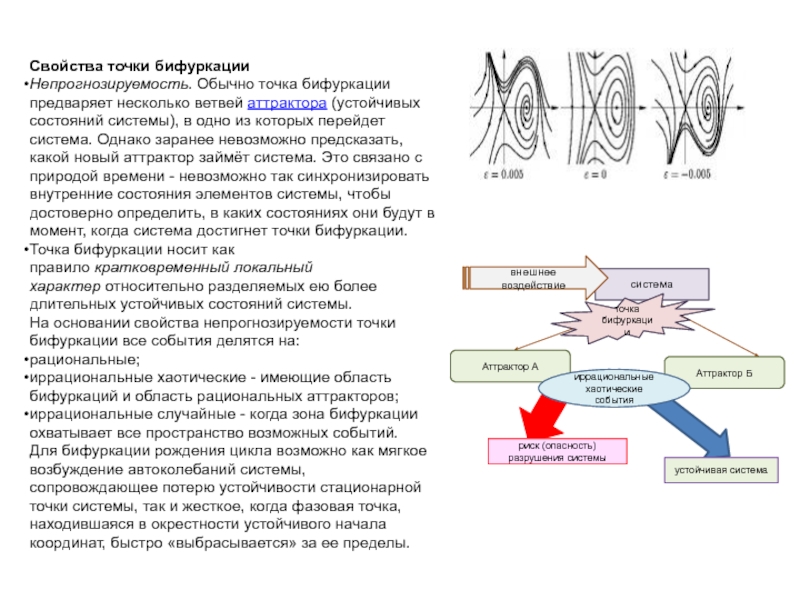
Слайд 13Свойства точки бифуркации
Непрогнозируемость. Обычно точка бифуркации предваряет несколько ветвей аттрактора (устойчивых состояний системы),
в одно из которых перейдет система. Однако заранее невозможно предсказать,
какой новый аттрактор займёт система. Это связано с природой времени - невозможно так синхронизировать внутренние состояния элементов системы, чтобы достоверно определить, в каких состояниях они будут в момент, когда система достигнет точки бифуркации.
Точка бифуркации носит как правило кратковременный локальный характер относительно разделяемых ею более длительных устойчивых состояний системы.
На основании свойства непрогнозируемости точки бифуркации все события делятся на:
рациональные;
иррациональные хаотические - имеющие область бифуркаций и область рациональных аттракторов;
иррациональные случайные - когда зона бифуркации охватывает все пространство возможных событий.
Для бифуркации рождения цикла возможно как мягкое возбуждение автоколебаний системы, сопровождающее потерю устойчивости стационарной точки системы, так и жесткое, когда фазовая точка, находившаяся в окрестности устойчивого начала координат, быстро «выбрасывается» за ее пределы.
Слайд 14«При подходе вплотную к точкам бифуркации флуктуации становятся аномально сильными
и закон больших чисел нарушается. Этого следовало ожидать, так как
в сильно неравновесной области система при прохождении точек бифуркации "выбирает" один из различных, возможных режимов. Амплитуды флуктуаций имеют такой же порядок величины, как и средние макроскопические значения. Следовательно, различие между флуктуациями и средними значениями стирается» (И. Пригожин), реализуется опасность разрушения системы, т.е. «в результате фазового перехода второго рода кооперативное поведение большого числа подсистем приведет к возникновению микросостояния со спонтанно нарушенной симметрией».
«При уходе системы от состояния равновесия она может пройти через несколько зон неустойчивости. В каждой из них поведение системы качественно изменяется, система может перейти в "хаотическое" состояние, в котором ее поведение лучше всего символизирует то новое, что привнесла в концепции порядка и беспорядка сильно неравновесная физика: оба состояния - и порядка, и беспорядка - когерентны, что означает, что для обоих характерны действующие корреляции и оба состояния непредсказуемы» (И. Пригожин).

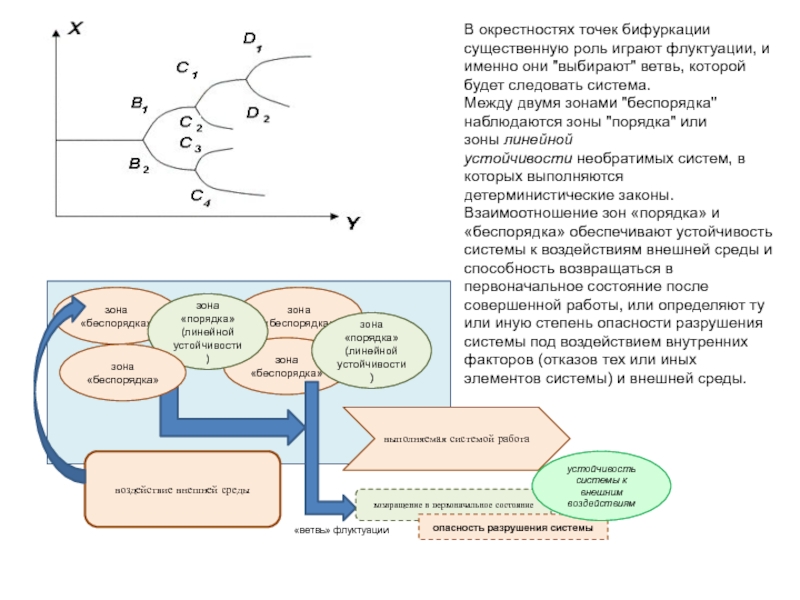
Слайд 15В окрестностях точек бифуркации существенную роль играют флуктуации, и именно
они "выбирают" ветвь, которой будет следовать система.
Между двумя зонами "беспорядка"
наблюдаются зоны "порядка" или зоны линейной устойчивости необратимых систем, в которых выполняются детерминистические законы.
Взаимоотношение зон «порядка» и «беспорядка» обеспечивают устойчивость системы к воздействиям внешней среды и способность возвращаться в первоначальное состояние после совершенной работы, или определяют ту или иную степень опасности разрушения системы под воздействием внутренних факторов (отказов тех или иных элементов системы) и внешней среды.
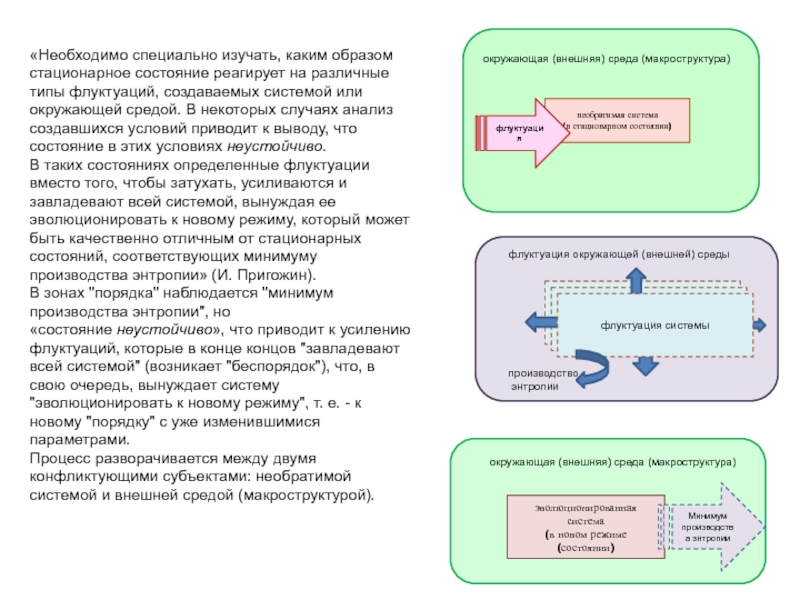
Слайд 16«Необходимо специально изучать, каким образом стационарное состояние реагирует на различные
типы флуктуаций, создаваемых системой или окружающей средой. В некоторых случаях
анализ создавшихся условий приводит к выводу, что состояние в этих условиях неустойчиво.
В таких состояниях определенные флуктуации вместо того, чтобы затухать, усиливаются и завладевают всей системой, вынуждая ее эволюционировать к новому режиму, который может быть качественно отличным от стационарных состояний, соответствующих минимуму производства энтропии» (И. Пригожин).
В зонах "порядка" наблюдается "минимум производства энтропии", но «состояние неустойчиво», что приводит к усилению флуктуаций, которые в конце концов "завладевают всей системой" (возникает "беспорядок"), что, в свою очередь, вынуждает систему "эволюционировать к новому режиму", т. е. - к новому "порядку" с уже изменившимися параметрами.
Процесс разворачивается между двумя конфликтующими субъектами: необратимой системой и внешней средой (макроструктурой).
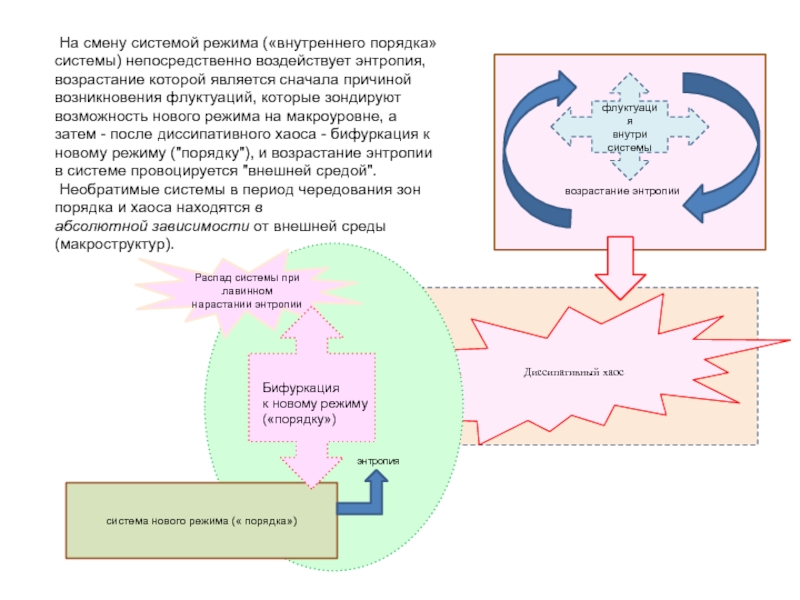
Слайд 17 На смену системой режима («внутреннего порядка» системы) непосредственно воздействует
энтропия, возрастание которой является сначала причиной возникновения флуктуаций, которые зондируют
возможность нового режима на макроуровне, а затем - после диссипативного хаоса - бифуркация к новому режиму ("порядку"), и возрастание энтропии в системе провоцируется "внешней средой".
Необратимые системы в период чередования зон порядка и хаоса находятся в абсолютной зависимости от внешней среды (макроструктур).
Слайд 18Энтропия - функция состояния, поэтому изменение энтропии системы не зависит
от того, как совершался процесс - обратимо или необратимо. Изменение
энтропии газа при необратимом расширении против внешнего давления будет таким же, как и при обратимом расширении. Другое дело - энтропия окружающей среды, которую можно найти, рассчитав с помощью первого закона теплоту, переданную системе:
при этом ∆U = 0 (температура постоянна).
Работа, совершаемая системой против постоянного внешнего давления равна:
A = p(V2-V1),
а теплота, принятая окружающей средой, равна работе, совершенной системой, с обратным знаком.
Общее изменение энтропии газа и окружающей среды больше 0:
как и полагается для необратимого процесса.
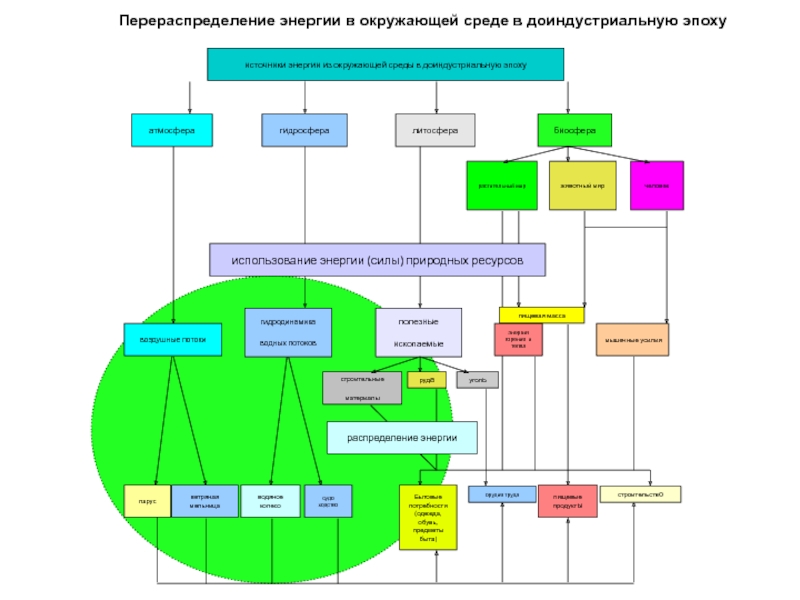
Слайд 19Перераспределение энергии в окружающей среде в доиндустриальную эпоху
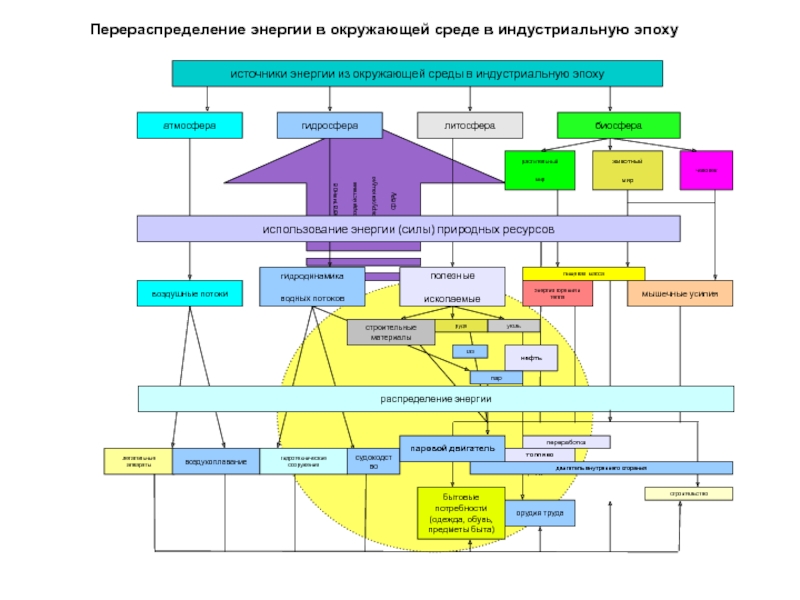
Слайд 20Перераспределение энергии в окружающей среде в индустриальную эпоху
Слайд 21Внутренние влияния на биосферу как замкнутую систему выражаются в факторах
воздействия внутренней энергии Земли и антропогенного воздействия непосредственно или через
техносферу .
Особенно явно это проявилось через потребление источников энергии непосредственно из окружающей среды.
Свободная энергия F для биосферы как замкнутой системы выражается:
F=U-TS
где:
Т – температура (стабилизируется за счет теплообмена с окружающей средой);
S – энтропия;
U – внутренняя энергия биосферы как замкнутой системы;
F – свободная энергия.
Так как свободная энергия должна стремиться к минимуму, то снижению энтропии, как мере беспорядка, соответствует рост температуры окружающей среды, наблюдаемый в последнее время в результате антропогенной деятельности не только в природных средах (атмосфере, верхних слоях литосферы), но особенно высокое содержание энергии и температурных показателей наблюдается в местах скопления людей и продуктов их жизнедеятельности – в населенных пунктах и промышленных зонах, т. е. в техносфере.
Внутренняя энергия биосферы постоянно возрастает за счет используемой в ней и свободной энергии, при этом свободная энергоемкость биосферы как замкнутой системы снижается, а, следовательно, растет энтропия.

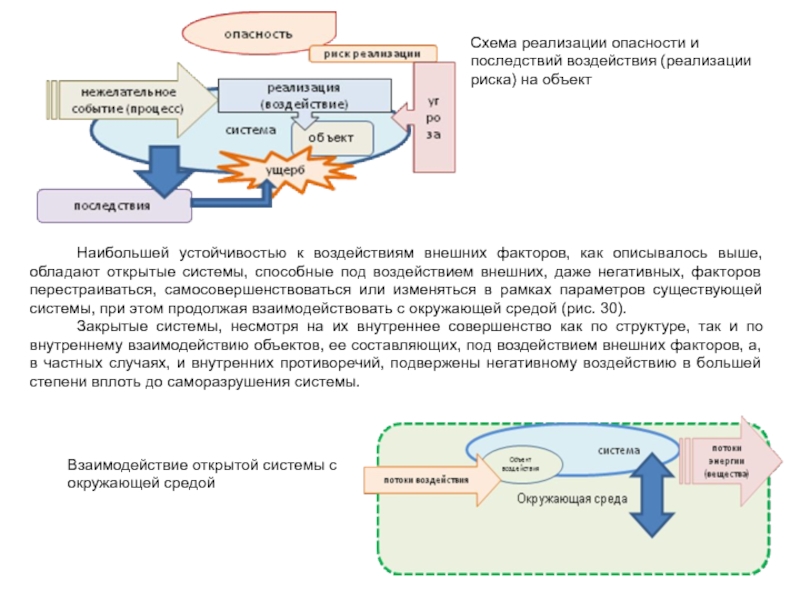
Слайд 22Схема реализации опасности и последствий воздействия (реализации риска) на объект
Наибольшей
устойчивостью к воздействиям внешних факторов, как описывалось выше, обладают открытые
системы, способные под воздействием внешних, даже негативных, факторов перестраиваться, самосовершенствоваться или изменяться в рамках параметров существующей системы, при этом продолжая взаимодействовать с окружающей средой (рис. 30).
Закрытые системы, несмотря на их внутреннее совершенство как по структуре, так и по внутреннему взаимодействию объектов, ее составляющих, под воздействием внешних факторов, а, в частных случаях, и внутренних противоречий, подвержены негативному воздействию в большей степени вплоть до саморазрушения системы.
Взаимодействие открытой системы с окружающей средой
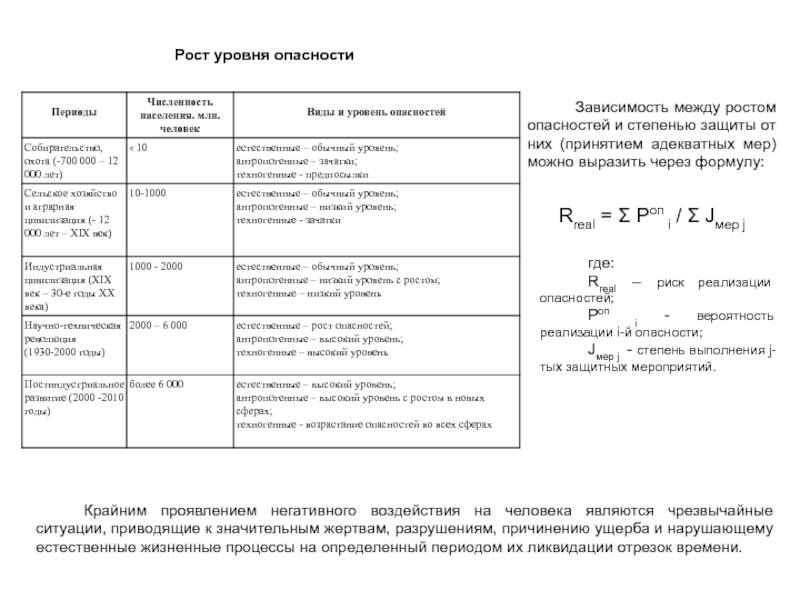
Слайд 23Рост уровня опасности
Зависимость между ростом опасностей и степенью защиты
от них (принятием адекватных мер) можно выразить через формулу:
Rreal =
Σ Роп i / Σ Jмер j
где:
Rreal – риск реализации опасностей;
Роп i - вероятность реализации i-й опасности;
Jмер j - степень выполнения j-тых защитных мероприятий.
Крайним проявлением негативного воздействия на человека являются чрезвычайные ситуации, приводящие к значительным жертвам, разрушениям, причинению ущерба и нарушающему естественные жизненные процессы на определенный периодом их ликвидации отрезок времени.