Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Эйлеров граф (Эйлеров цикл, Эйлеров путь)
Содержание
- 1. Эйлеров граф (Эйлеров цикл, Эйлеров путь)
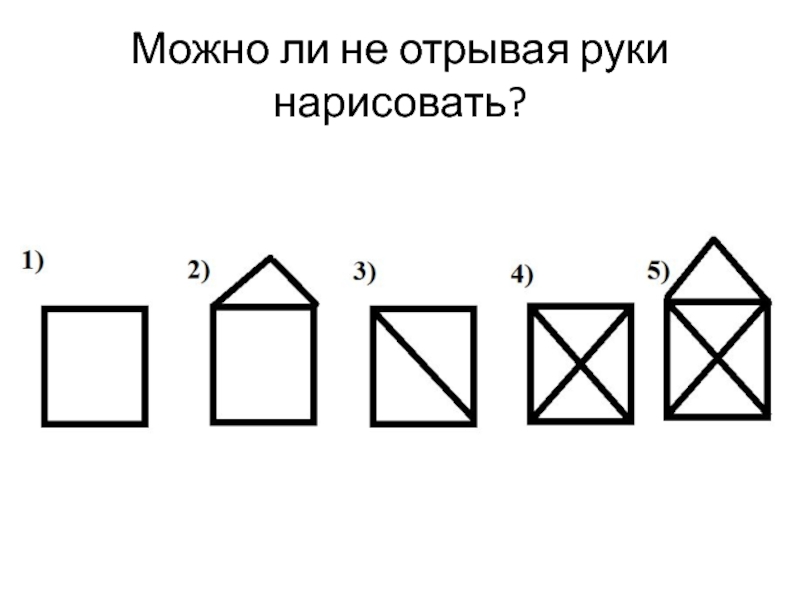
- 2. Можно ли не отрывая руки нарисовать?
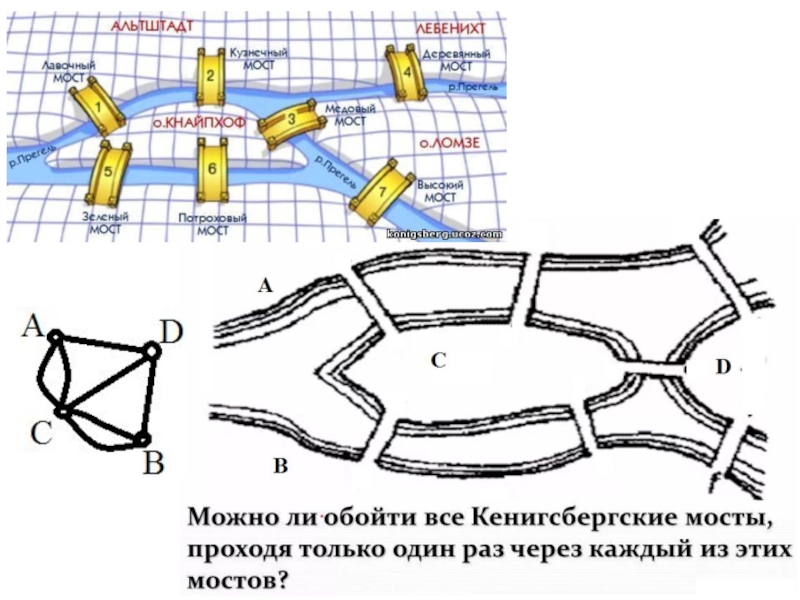
- 3. Слайд 3
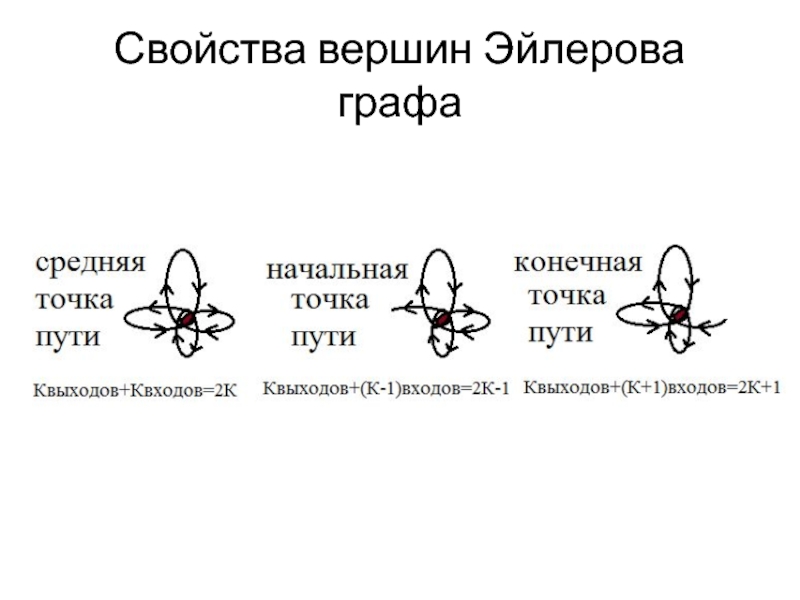
- 4. Свойства вершин Эйлерова графа
- 5. 1-ое свойство Эйлеровых графовВ Эйлеровом графе число
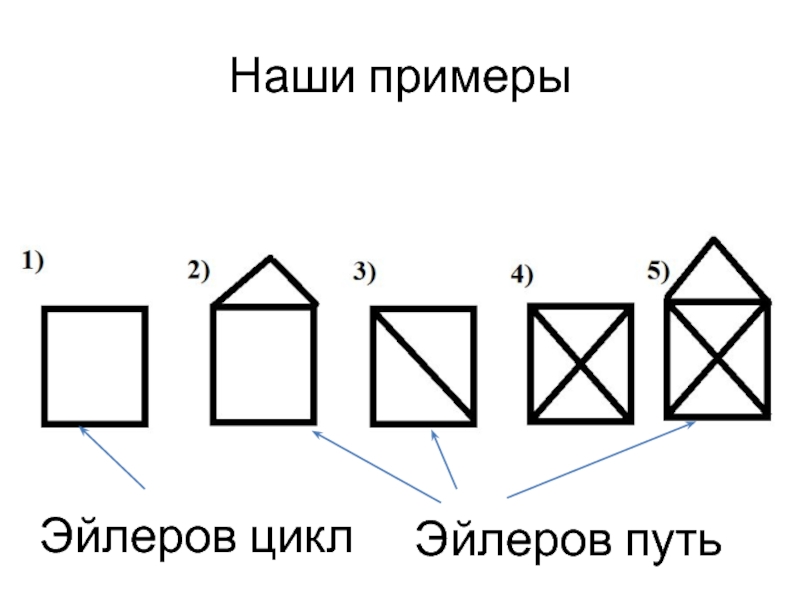
- 6. Наши примерыЭйлеров циклЭйлеров путь
- 7. Структура данныхint i,j, n, //
- 8. Подсчет степенейfor (i=1;i
- 9. Выполнение первого свойстваif (k==0) cout
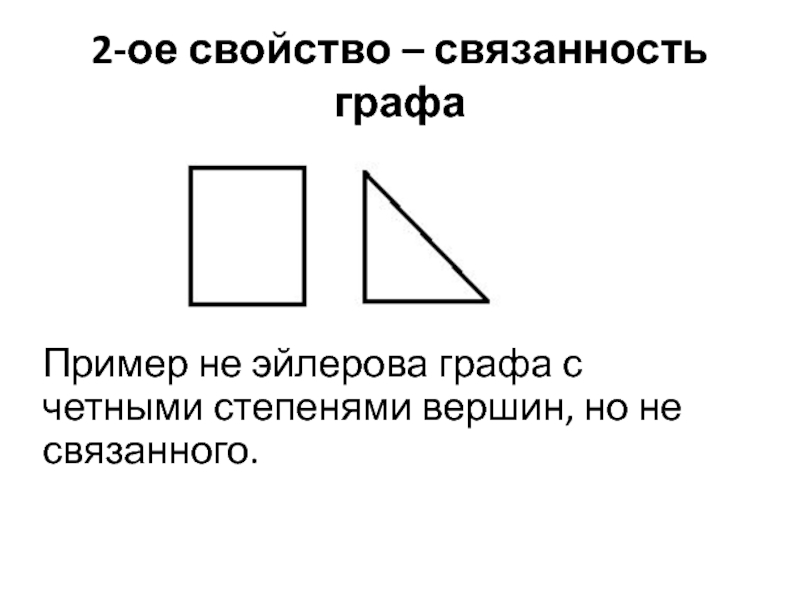
- 10. 2-ое свойство – связанность графаПример не эйлерова графа с четными степенями вершин, но не связанного.
- 11. 2-е свойство связанностиint Q[100]={1}; // Выявление компонент// связанности (КС). 1 – не связанная вершинаfor (i=1;i
- 12. 2-ое свойство связанностиint p[100], m=1; //
- 13. 2-ое свойство связанностиInt z=0; //число нерасмотренных
- 14. Скачать презентанцию
Можно ли не отрывая руки нарисовать?
Слайды и текст этой презентации
Слайд 1Эйлеров граф
(Эйлеров цикл, Эйлеров путь)
Старший преподаватель
кафедры теоретической кибернетики
Хадиев Р.М.
КАЗАНСКИЙ ФЕДЕРАЛЬНЫЙ
УНИВЕРСИТЕТ
Слайд 51-ое свойство Эйлеровых графов
В Эйлеровом графе число вершин с нечетной
степенью равно 0 (условие существования эйлерова цикла)
В полуэйлеровом графе число
вершин с нечетной степенью равно 2 (условие существования эйлерова пути в графе)
Слайд 7Структура данных
int i,j,
n, // число вершин
G[100][100], //G[i][j]=1 – наличие моста
R[100], //
степень вершины – число мостовcin >> n;
// ввод данных
for (i=1;i<=n; i++)
for (j=1;j<=n; j++)
cin >> G[i][j]
![Структура данныхint i,j, n, // число вершин G[100][100], //G[i][j]=1 – наличие моста](/img/tmb/3/245403/81cb8ed47c6f914b7ec013acbfbd0af4-800x.jpg "Эйлеров граф (Эйлеров цикл, Эйлеров путь) Структура данныхint i,j, n, // число вершин G[100][100], //G[i][j]=1")
Слайд 8Подсчет степеней
for (i=1;i
R[i]+=G[i][j];
}
int k=0; // число вершин с нечетной степенью
for
(i=1;i<=n;i++) k+=R[i]%2;
Слайд 102-ое свойство – связанность графа
Пример не эйлерова графа с четными
степенями вершин, но не связанного.
Слайд 112-е свойство связанности
int Q[100]={1}; // Выявление компонент
// связанности (КС). 1
– не связанная вершина
for (i=1;i
вершинаi=1;
while (Q[i]==0 & i<=n) i++;
if (i>n) { cout << “вырожденный граф”; return 0;}
![2-е свойство связанностиint Q[100]={1}; // Выявление компонент// связанности (КС). 1 – не связанная вершинаfor (i=1;i](/img/thumbs/670a29d3f793e555f992d8a50552dc7c-800x.jpg "Эйлеров граф (Эйлеров цикл, Эйлеров путь) 2-е свойство связанностиint Q[100]={1}; // Выявление компонент// связанности (КС). 1 – не связанная вершинаfor (i=1;i")
Слайд 122-ое свойство связанности
int p[100],
m=1; // число элементов КС
a=1; // анализируемый элемент КС
P[1]=i; // первый
элемент КСwhile (a<=m) {
for (i=1;i<=n;i++)
if (Q[i]==1 & G[i][P[a]]==1) {
m++; // включение i в компоненту свсязанности
P[m]=i;
Q[i]=0; // исключение i из дальнейшего рассмотрения
}
a++; // переход
}
![2-ое свойство связанностиint p[100], m=1; // число элементов КС a=1; // анализируемый элемент КС](/img/tmb/3/245403/067d520235e2af434c22103ca76838f4-800x.jpg "Эйлеров граф (Эйлеров цикл, Эйлеров путь) 2-ое свойство связанностиint p[100], m=1; // число элементов КС a=1; //")
Слайд 132-ое свойство связанности
Int z=0; //число нерасмотренных
// островов с мостами
for ( int
i=1; i<=n; i++)z+=Q[i];
if (z>0) cout << “Не эйлеров граф”;
else if (k==0) cout << “Эйлеров граф”;
else cout << “Полуэйлеров граф”;
