Слайд 1Факторный анализ
Выполнили студентки
5 курса 57 группы ФМИТ
Буранбаева Л.Ф.
Елкибаева Г.Г.
Слайд 2История возникновения факторного анализа
Факторный анализ своими корнями связан
с научным
мировоззрением второй половины
XIX столетия. Но началом современного этапа в
развитии факторного анализа принято
считать статью Спирмэна, опубликованную в 1904
г. под названием "General intelligence objectively
determined and measured". Спирмэн исходил из
того, что один генеральный фактор, обозначенный
им буквой g, и один характерный фактор оказывают
решающее влияние на все интеллектуальные возможности. Он пытался проверить эту психологическую теорию с помощью своей простой факторной модели. Корреляции между различными психологическими тестами, с помощью которых контролировались интеллектуальные возможности, он объяснял генеральным фактором g и для каждого теста выделял один дополнительный характерный фактор. Эта так называемая двухфакторная теория через некоторое время, когда психологи начали работать с большими наборами психологических тестов, оказалась несовершенной.
Слайд 3Хользингер в своей бифакторной теории пытался преодолеть недостатки, присущие двухфакторной
теории. В свою модель кроме генерального и характерных факторов он
включил групповые. Однако концепция одного генерального фактора оказалась несостоятельной, и дальнейшее развитие теории привело, наконец, к так называемому многофакторному анализу Тэрстоуна. Тэрстоун не был первым, кто выделил несколько факторов из корреляционной матрицы. Но он внес значительный вклад в развитие теории, указав, что минимально необходимое число факторов соответствует рангу корреляционной матрицы. Использование Тэрстоуном матричной алгебры явилось переломным моментом в истории факторного анализа, позволив по-новому трактовать основные его положения.
В первые десятилетия XX столетия на развитие факторного анализа оказали влияние работы С. Барта, К. Пирсона, Г. Томсона, Д. Гарнетта и К. Хользингера.
В последние десятилетия на развитие факторного анализа оказывает сильное влияние математическая статистика и применение ЭВМ. Современный этап развития факторного анализа характеризуется исследованием многих частных проблем с различными моделями.

Слайд 4Факторный анализ
Факторный анализ - многомерный метод, применяемый для изучения взаимосвязей
между значениями переменных.
Предполагается, что известные переменные зависят от меньшего
количества неизвестных переменных и случайной ошибки.
Основные задачи факторного анализа:
-отбор факторов, которые определяют исследование нормативного показателя;
-их классификация и систематизация с целью обеспечения возможности системного подхода;
- определение формы зависимости между факторами и результативным показателем;
-моделирование взаимосвязей между результативным и факторным показателями;
-расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя;
-работа с факторной моделью, т.е. ее практическое использование для управления экономическими процессами.
Слайд 5Типы факторного анализа
1. Детерминированный (функциональный) – результативный показатель представлен в
виде произведения, частного или алгебраической суммы факторов;
2. Стохастический (корреляционный) –
связь между результативным и факторными показателями является неполной или вероятностной;
3. Прямой (дедуктивный) – от общего к частному;
4. Обратный (индуктивный) – от частного к общему;
5. Одноступенчатый и многоступенчатый;
6. Статический и динамический (статический применяется при изучении влияния факторов на результативные показатели на соответствующую дату; динамический представляет собой методику исследования причинно-следственных связей в динамике);
7. Ретроспективный и перспективный (ретроспективный изучает причины прироста результативных показателей за прошлые периоды; перспективный исследует поведение факторов и результативных показателей в перспективе)
Слайд 6Этапы факторного анализа
1 этап - отбор факторов;
2 этап - классификация
и систематизация факторов;
3 этап - моделирование взаимосвязей между результативным и
факторными показателями;
4 этап - расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя;
5 этап - практическое использование факторной модели (подсчет резервов прироста результативного показателя).
Слайд 7Классификация и систематизация факторов
Классификация факторов по признакам:
по своей природе:
- основные;
-
второстепенные;
по степени воздействия на результаты:
- основные
- второстепенные;
по отношению к объекту
исследования:
- внутренние;
- внешние;
по зависимости от коллектива:
- объективные;
- субъективные;
по степени распространенности:
- общие;
- специфические;
по времени действия:
- постоянные;
- переменные;
по характеру действия:
- экстенсивные;
- интенсивные;
по свойствам отражаемых явлений:
- количественные;
- качественные;
по своему составу:
- сложные;
- простые;
по уровню соподчиненности:
- первого порядка;
- второго порядка;- и т.д.
по возможности измерения влияния:
- измеримые;
- неизмеримые.
Слайд 8Стохастический факторный анализ представляет собой методику исследования факторов, связь которых
с результативным показателем в отличие от функциональной является неполной, вероятностной
(корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при корреляционной связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель.
Стохастический
факторный анализ
Методы стохастического факторного анализа:
1. Способ парной корреляции;
2. Множественный корреляционный анализ;
3. Матричные модели;
4. Математическое программирование;
5. Метод исследования операций;
6. Теория игр.
Слайд 9Способ парной корреляции и множественный корреляционный анализ
Метод корреляционного и регрессионного
(стохастического) анализа широко используется для определения тесноты связи между показателями,
не находящимися в функциональной зависимости, т.е. связь проявляется не в каждом отдельном случае, а в определенной зависимости.
С помощью корреляции решаются две главные задачи:
1) составляется модель действующих факторов (уравнение регрессии);
2) дается количественная оценка тесноты связей (коэффициент корреляции).
Коэффициент парной корреляции оценивает значимость тех или иных факторов для данного объекта исследования, что позволяет уменьшить количество входных параметров и оценить влияние факторов на целевые функции;
Коэффициент множественной корреляции показывает степень статистической зависимости между наблюдаемыми значениями отклика и их предсказаниями по модели (позволяет проверить адекватность построенной модели).
Слайд 10Матричные модели
Матричные модели представляют собой схематическое отражение экономического
явления или процесса с помощью научной абстракции. Наибольшее распространение здесь
получил метод анализа«затраты-выпуск», строящийся по шахматной схеме и позволяющий в наиболее компактной форме представить взаимосвязь затрат и результатов производства.
Математическое программирование
Математическое программирование– это основное средство решения задач по оптимизации производственно-хозяйственной деятельности.
Метод исследования операций
Метод исследования операций направлен на изучение экономических систем, в том числе производственно-хозяйственной деятельности предприятий, с целью определения такого сочетания структурных взаимосвязанных элементов систем, которое в наибольшей степени позволит определить наилучший экономический показатель из ряда возможных.
Теория игр
Теория игр как раздел исследования операций- это теория математических моделей принятия оптимальных решений в условиях неопределенности или конфликта нескольких сторон, имеющих различные интересы.
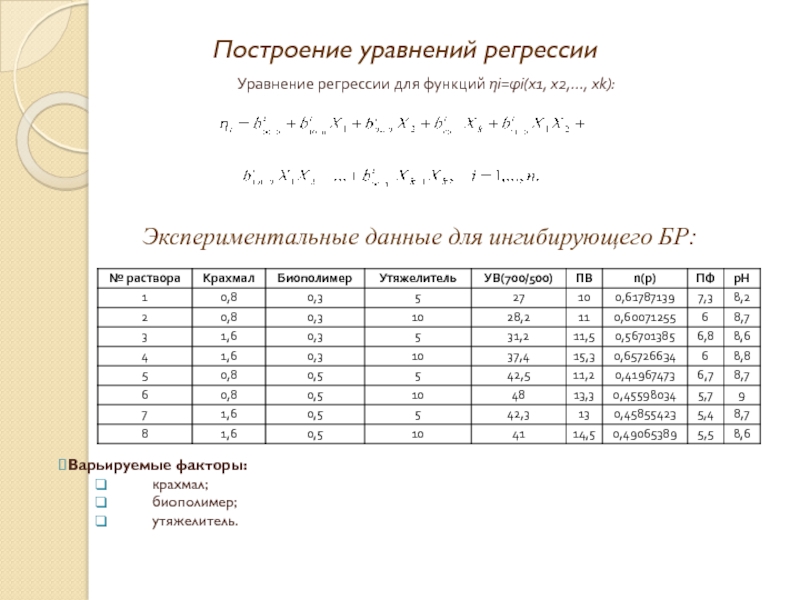
Слайд 11Построение уравнений регрессии
Уравнение регрессии для функций ηi=φi(x1, x2,…, xk):
Варьируемые факторы:
крахмал;
биополимер;
утяжелитель.
Моделируемые параметры раствора:
плотность раствора;
условная вязкость;
коэффициент
нелинейности;
пластическая вязкость;
показатель фильтрации;
pH-показатель.
Экспериментальные данные для ингибирующего БР:
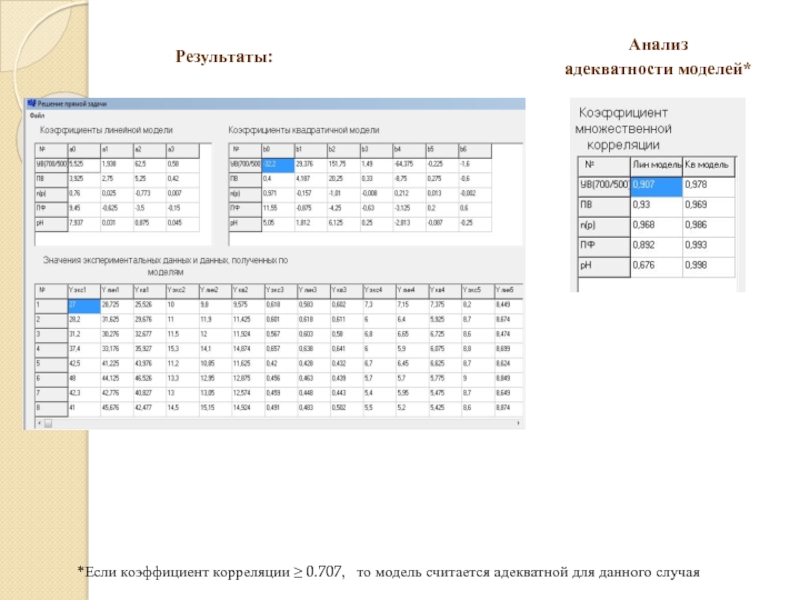
Слайд 12Результаты:
Анализ
адекватности моделей*
*Если коэффициент корреляции ≥ 0.707, то модель
считается адекватной для данного случая
Слайд 13Детерминированный факторный анализ
Детерминированный факторный анализ представляет собой методику исследования влияния
факторов, связь которых с результативным показателем носит функциональный характер, т.
е. когда результативный показатель факторной модели представлен в виде произведения, частного или алгебраической суммы факторов.
Методы детерминированного факторного анализа:
Метод цепных подстановок;
Метод абсолютных разниц;
Метод относительных разниц;
Интегральный метод;
Метод логарифмирования.
Данный вид факторного анализа наиболее распространен, поскольку, будучи достаточно простым в применении (по сравнению со стохастическим анализом), позволяет осознать логику действия основных факторов развития предприятия, количественно оценить их влияние, понять, какие факторы, и в какой пропорции возможно и целесообразно изменить для повышения эффективности производства.
Слайд 14Метод цепных подстановок
Метод цепных подстановок заключается в определении ряда промежуточных
значений результативного показателя путем последовательной замены базисных значений факторов на
отчетные. Данный способ основан на элиминировании.
Элиминировать – значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного.
Метод цепных подстановок является наиболее универсалmным из методов элиминирования.
Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде.
С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

Слайд 15В общем виде применение способа цепных постановок можно описать следующим
образом:
y0=a0*b0*c0
ya=a1*b0*c0
yb=a1*b1*c0
y1=a1*b1*c1
где a0, b0, c0 - базисные значения факторов, оказывающих
влияние на обобщающий показатель у;
a, b1, c1- фактические значения факторов;
ya , yb, - промежуточные изменения результирующего показателя, связанного с изменением факторов а, b соответственно.
Общее изменение Δу=у1–у0 складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:
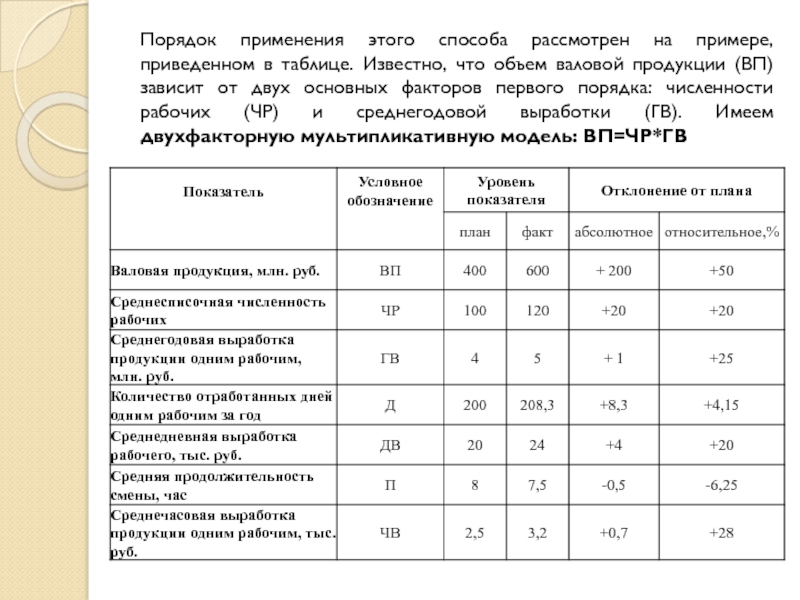
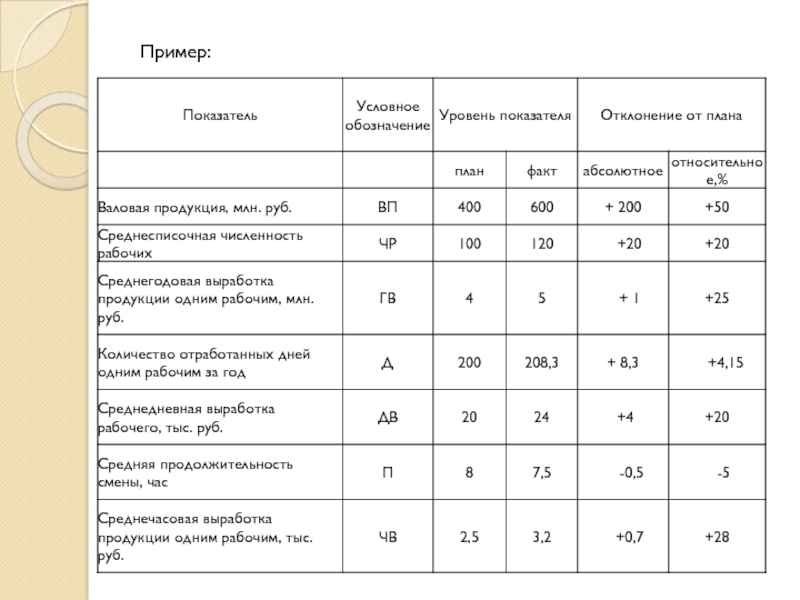
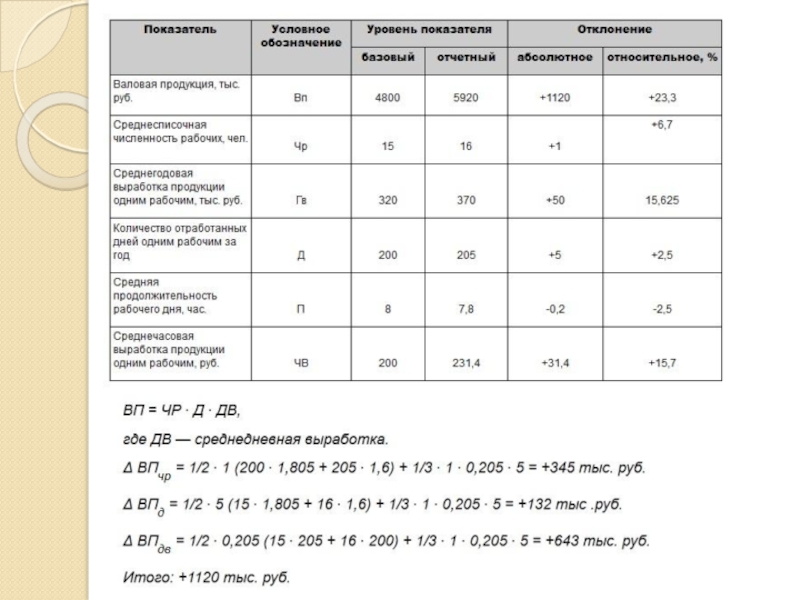
Слайд 16Порядок применения этого способа рассмотрен на примере, приведенном в таблице.
Известно, что объем валовой продукции (ВП) зависит от двух основных
факторов первого порядка: численности рабочих (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель: ВП=ЧР*ГВ
Слайд 17Алгоритм расчета способом цепной подстановки для этой модели:
Как видно, второй показатель валовой
продукции отличается от первого тем, что при его расчете принята
фактическая численность рабочих вместо плановой. Среднегодовая выработка продукции одним рабочим в том и другом случае плановая. Значит, за счет роста численности рабочих выпуск продукции увеличился на 80 млн. руб. (480 – 400).
Третий показатель валовой продукции отличается от второго тем, что при расчете его величины выработка рабочих принята по фактическому уровню вместо планового. Количество же работников в обоих случаях фактическое. Отсюда: за счет повышения производительности труда объем валовой продукции увеличился на 120 млн. руб. (600 — 480).
Слайд 18Таким образом, перевыполнение плана по объему валовой продукции явилось результатом
влияния следующих факторов:
а) увеличения численности рабочих + 80 млн. руб.
б) повышения
уровня производительности труда + 120 млн. руб.
Итого + 200 млн. руб.
Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:
Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.
Преимущества данного способа: универсальность применения, простота расчетов.
Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения.
Слайд 19Метод абсолютных разниц
Метод абсолютных разниц является модификацией способа цепной подстановки.
Изменение результативного показателя за счет каждого фактора определяется как произведение
абсолютного прироста исследуемого фактора на базисную величину факторов, которые находятся справа от него и отчетную величину факторов, расположенных слева от него в модели.
Слайд 21Алгоритм расчета для мультипликативной четырехфакторной модели валовой продукции выглядит следующим
образом:
План по выпуску продукции в целом перевыполнен на 200 млн.
руб. (600 – 400), в том числе за счет изменения:
количества рабочих ΔВПчр = + 80
количества отработанных дней одним рабочим за год ΔВПД = +20
средней продолжительности рабочего дня ΔВПП = — 31,25
среднечасовой выработки ΔВПЧВ = -131,25
ΔВП = ΔВПчр + ΔВПД + ΔВПП + ΔВПЧВ = + 80 +20 — 31,25 + 131,25 = +200
Всего: +200 млн. руб.
Таким образом, с помощью способа абсолютных разниц получаются те же результаты, что и способом цветной подстановки.
Слайд 22Метод относительных разниц
Метод относительных разниц также является одной из модификацией
способа цепной подстановки. Применяется для измерения влияния факторов на прирост
результативного показателя в мультипликативных моделях. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах. Для мультипликативных моделей типа
у = а*b*с методика анализа следующая:
Находят относительное отклонение каждого факторного показателя:
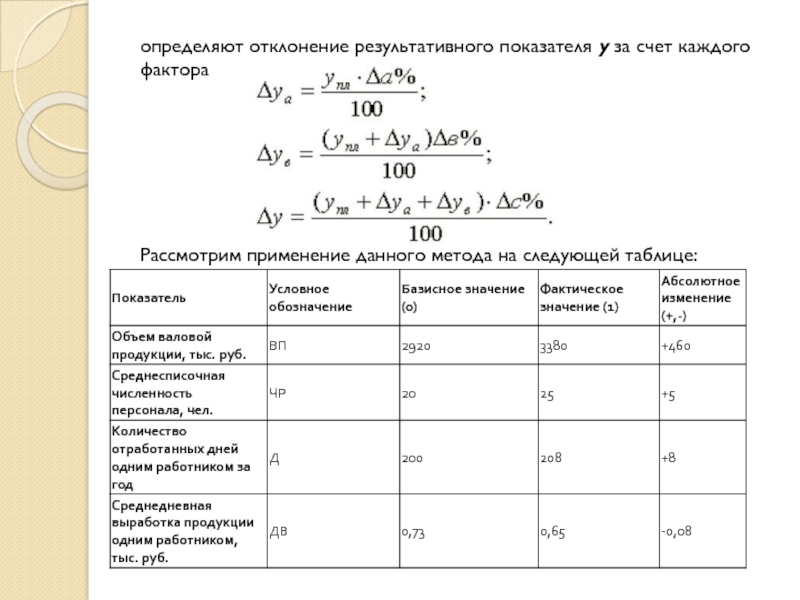
Слайд 23определяют отклонение результативного показателя у за счет каждого фактора
Рассмотрим применение
данного метода на следующей таблице:
Слайд 24Зависимость объема производства продукции от данных факторов выражается трехфакторной мультипликативной
моделью:
ВП = ЧР * Д*ДВ.
Определяем относительные отклонения рассматриваемых факторов:
ΔЧР% =
((ЧР1-ЧР0)/ЧР0)*100% = ((25-20)/20)*100% = 25%;
ΔД% = ((Д1-Д0)/Д0)*100% = ((208-200)/200)*100% = 4%;
ΔДВ% = ((ДВ1-ДВ0)/ДВ0)*100% = ((0,65-0,73)/0,73)*100% = -10,96%;
Рассчитаем влияние каждого фактора на валовый объем производства:
ΔВП(ЧР) = ВП0* ΔЧР%/100 = 2920*25/100 = 730 тыс. руб. - влияние изменения количества работников;
ΔВП(Д) = (ВП0+ΔВП(ЧР))* ΔД%/100 = (2920+730)*4/100 = 146 тыс. руб. - влияние изменения количества отработанных дней одним работником;
ΔВП(ДВ) = (ВП0+ΔВП(ЧР)+ΔВП(Д))*ΔДВ%/100 = (2920+730+146)*(-10,96)/100 = -416,04 ≈ -416 тыс. руб. - влияние изменения величины среднедневной выработки продукции одним работником;
Суммарное влияние трех факторов определим по формуле:
ΔВП = ΔВП(ЧР) + ΔВП(Д) + ΔВП(ДВ) = 730+146+(-416) = 460 тыс. руб. - значение совпадает с табличным и подтверждает правильность расчетов.
Слайд 25Вывод. Таким образом, на изменение объема производства продукции положительное влияние
оказало увеличение на 5 человек численности работников, что вызвало увеличение
объема производства на 730 тыс. руб. и увеличение количества отработанных дней на 8 каждым работником, что вызвало увеличение объема производства на 146 тыс. руб.
Отрицательное влияние оказало снижение среднедневной выработки на 80 руб., что вызвало снижение объема производства на 416 тыс. руб.
Суммарное влияние трех факторов привело к увеличению объема производства на 460 тыс. руб.
Слайд 26Интегральный метод
Интегральный метод применим к мультипликативным, кратным и смешанным моделям.
Метод позволяет получать более точные результаты расчета влияния факторов по
сравнению с методами цепной подстановки, абсолютных и относительных разниц. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. Можно использовать также уже сформированные рабочие формулы, приводимые в специальной литературе:
1.Модель вида:
Слайд 272.Модель вида:
3. Модель вида:
И т.д.
Рассмотрим следующий пример:
Слайд 29Метод логарифмирования
Метод логарифмирования применяется для измерения влияния факторов только в
мультипликативных моделях. Данный метод обеспечивает высокую точность расчетов. При этом
результаты не зависят от местоположения факторов в модели. Дополнительный прирост от взаимодействия факторов распределяется пропорционально доле изолированного влияния каждого фактора на уровень результативного показателя (пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя). При расчетах используются как натуральный, так и десятичный логарифм. При логарифмировании, в отличии от интегрирования. Используются не абсолютные приросты показателей, а индексы их роста (снижения).
Пусть, результативный показатель можно представить в виде произведения трех факторов: f=xyz
Влияние данных факторов определяется следующим способом:
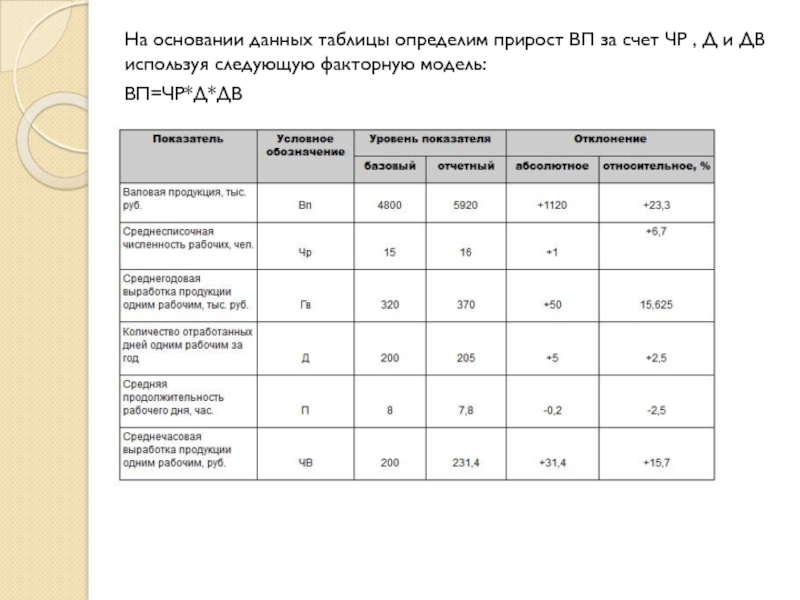
Слайд 30На основании данных таблицы определим прирост ВП за счет ЧР
, Д и ДВ используя следующую факторную модель:
ВП=ЧР*Д*ДВ
Слайд 31
Преимущество данного метода состоит в относительной простоте вычислений и более
высокой точности расчетов.
Слайд 32Выводы
Т.о., основная цель применения экономического факторного анализа заключается в вычислении
влияния изменения факторов, определяющих поведение системы, на изменение результирующего показателя.
Это анализ позволяет выявить на ранней стадии нарушение рабочего процесса в различных объектах, которое часто невозможно заметить путем непосредственного наблюдения за параметрами. Применение методики факторного анализа не ограничено физическими особенностями процессов, происходящих в объектах, и поэтому она может быть использована при исследовании самых различных явлений и процессов в технике, биологии, экономике, психологии, социологии и т.д..