Слайд 1Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Владимирский государственный университет
имени Александра Григорьевича
и Николая Григорьевича Столетовых”
(ВлГУ)
Методика изучения площади геометрической фигуры в процессе
изучения геометрического материала
Выполнила:
студентка группы ЗНОЛу-117
Куракина Анастасия Павловна
Проверила:
старший преподаватель
Болотова Татьяна Владимировна
Слайд 2 Площадь фигуры-это величина, которая характеризует, то место , которое
занимает предмет на поверхности чего-либо.
Слайд 3Задачи:
Формирование геометрических представлений;
Формирование пространственных представлений и развитие воображения, умений наблюдать,
сравнивать, обобщать;
Выработка у учащихся практических навыков измерения и построения геометрических
фигур с помощью измерительных и чертёжных инструментов;
Формирование умений использовать наглядность в приобретении знаний.
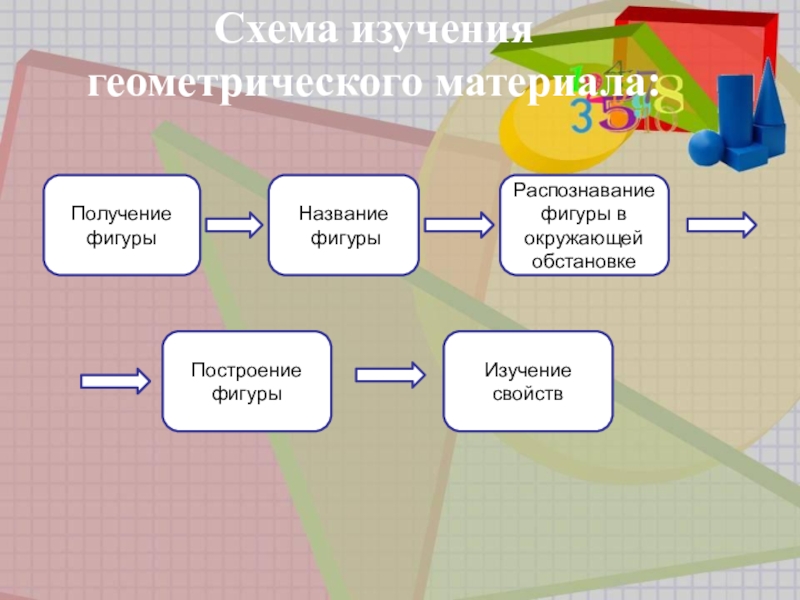
Слайд 4Схема изучения геометрического материала:
Получение
фигуры
Название
фигуры
Распознавание
фигуры в
окружающей
обстановке
Построение
фигуры
Изучение
свойств
Слайд 51 класс:
Точка
Линия (прямая, кривая)
Отрезок
Луч
Ломаная линия
Замкнутая линия
Незамкнутая линия
Слайд 62 класс:
Длина ломаной
Периметр многоугольника
Угол (прямой, тупой, острый)
Прямоугольник
Квадрат
Слайд 73 класс:
Обозначение геометрических фигур буквами
Площадь фигур, единицы площади
Окружность, круг (центр
окружности и круга; радиус и диаметр)
Виды треугольников (разносторонние, равнобедренные, равносторонние)
Слайд 84 класс:
Диагонали прямоугольника (квадрата) и их свойства
Геометрические тела (куб, параллелепипед,
пирамида, конус, цилиндр, шар)
Слайд 9Проекты:
1 класс
«Математика вокруг нас.
Форма, размер, цвет.
Узоры и орнаменты»
Слайд 10Проекты:
2 класс
«Математика вокруг нас.
Узоры и орнаменты
на посуде».
«Математика вокруг
нас.
Форма, размер, цвет.
Узоры и орнаменты»
Слайд 12Общая характеристика методики изучения площади в начальных классах.
Методика формирования представлений
о площади фигуры строится в соответствии с общей методикой формирования
представлений о величинах. При этом изучение понятия площади проводится с опорой на привычные для детей представления о том, что каждая фигура занимает определенное - большее или меньшее – место на плоскости.
Для разъяснения понятия используются демонстрационные или индивидуальные модели различных фигур .
Слайд 13
Путем наложения их друг на друга учащиеся устанавливают, что площади
первой и второй фигур одинаковы, а площадь четвертой меньше площади
пятой, так как вся четвертая фигура помещается внутри пятой, и т.д. учитель может предложить выписать номера фигур, расположив их в порядке возрастания площадей. в процессе таких упражнений уточняются представления детей о площади.
Слайд 14После этого учитель может раздать ученикам листы клетчатой бумаги, на
которой изображены различные фигуры и предложить сравнить площади этих фигур.
Учащиеся сами догадываются, что для этого нужно сосчитать число клеток в каждой фигуре. Фигура, содержащая большее число клеток, имеет большую площадь.
Такого рода задания подводят учащихся к осознанию необходимости введения общепринятой единицы площади 1 см2. (квадрат со стороной, равной одному сантиметру). У каждого ученика должна быть модель квадратного сантиметра.
Слайд 15 Для того чтобы учащиеся освоили процесс измерения площади
полезно раздать им геометрические фигуры и предложить им измерить их
площади, пользуясь моделью квадратного сантиметра. Это задание особенно важно, так как в процессе его выполнения учащиеся осознают, что измерить площадь фигуры – значит узнать, сколько квадратных сантиметров она содержит.
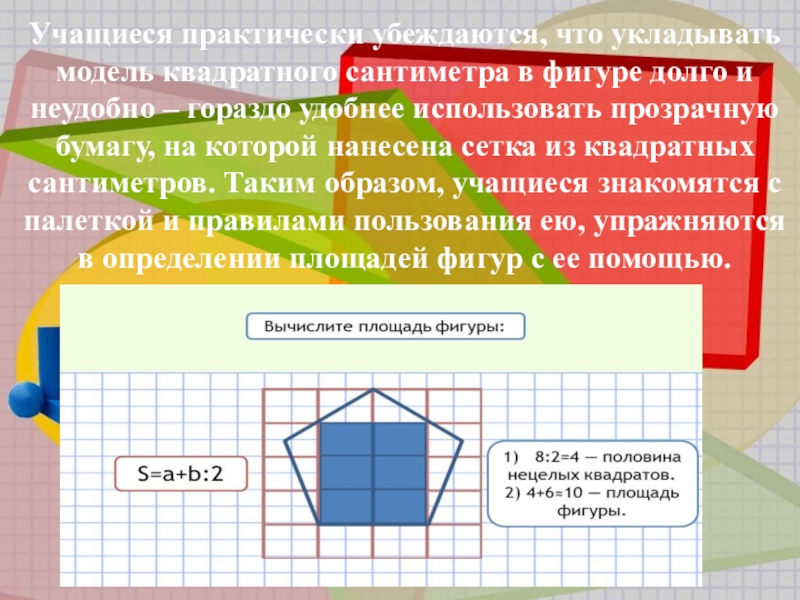
Слайд 16Учащиеся практически убеждаются, что укладывать модель квадратного сантиметра в фигуре
долго и неудобно – гораздо удобнее использовать прозрачную бумагу, на
которой нанесена сетка из квадратных сантиметров. Таким образом, учащиеся знакомятся с палеткой и правилами пользования ею, упражняются в определении площадей фигур с ее помощью.
Слайд 17Вывод:
При определении площади прямоугольника необходимо также широко использовать практический
метод. Это поможет учащимся осознать тот факт, что найти площадь
прямоугольника – значит узнать, сколько квадратных сантиметров в нем содержится.
Слайд 18Этапы работы изучения площади фигуры
1 этап.
-уточнение жизненных представлений детей о
площади, введение термина.
На доске прикреплены несколько кругов разного цвета
и разного размера, учитель предлагает сравнить их чем похожи? чем отличаются?
Слайд 192этап.
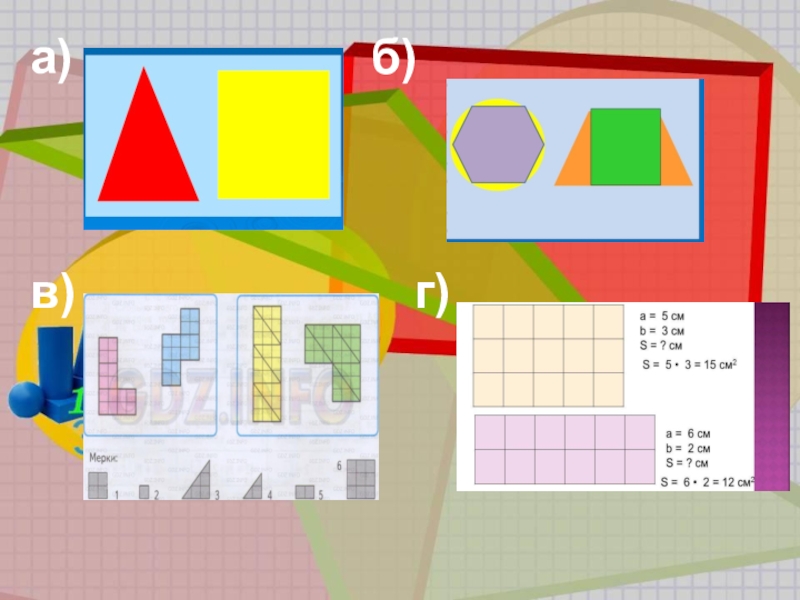
-сравнение фигур по площади разными спасобами
а)сравнить по площади предметы которые
сильно отличаются(на глаз)
б)сравнить по площади 2
фигуры одинаковые(наложением)
в) с помощью мерки
г)вычислением
Слайд 213 этап.
-введение единой меры площади см²
(Учащиеся чертят в тетрадях, вырезают
из бумаги в клеточку квадраты со стороной 1см. учитель сообщает:
"это единица площади – квадратный сантиметр«. Используя бумажные модели квадратного сантиметра, дети составляют из них различные геометрические фигуры и находят подсчетом их площадь)
Слайд 22-вводим правило нахождения площади прямоугольника
(сосчитать все нецелые квадратные сантиметры и
общее число их разделить на два, затем полученное число сложить
с числом целых квадратных сантиметров, которые содержатся в данной фигуре. Для нахождения площади геометрических фигур, не разделенных на квадратные сантиметры, используют палетку. Палетка – это прозрачная пластинка, разбитая на равные квадраты. Сетка может быть нанесена на кальку или состоять из нитей, натянутых на рамку. На данном этапе используют палетку, каждое деление которой равно квадратному сантиметру. Наложив палетку на геометрическую фигуру, подсчитывают число целых и нецелых квадратных сантиметров, которые в ней содержатся. )
Слайд 234 этап.
-сложение и вычитание величин выражения в см²
(Учащиеся знакомятся с
приемом вычисления площади прямоугольника (квадрата). Сначала рассматривают прямоугольники, которые уже
разделены на квадратные сантиметры. Их площадь находят путем подсчета квадратных сантиметров в одном ряду, а затем полученном число умножают на число рядов. Очень важно при этом установить соответствие между длиной прямоугольника и числом квадратных сантиметров, прилегающих к длине; шириной прямоугольника и числом рядов.)
22 см²+15 см²=37 см²
25 см²-10 см²=15 см²
Слайд 245 этап.
-введение других единиц измерения площади, соотношение между ними, перевод
из 1 единицы в другую
(нужно рассмотреть соотношение между этими мерами
и выучить их)
Слайд 25-введение специальных мер ар и гектар
Слайд 26Предлагаю задания на перевод величины из 1 единицы измерения в
другую
50
км²=5000000 м²
При переводе из крупных мер используем умножение, если наоборот деление
700 дм² = 70000 м²
570 дм² = 5м² 70дм.
Слайд 276 этап.
-сложение и вычитание величин выражающих в 2 единицах 2
наименований
а) устное сложение и вычитание когда нет перехода через меру,
выполняется в строчку
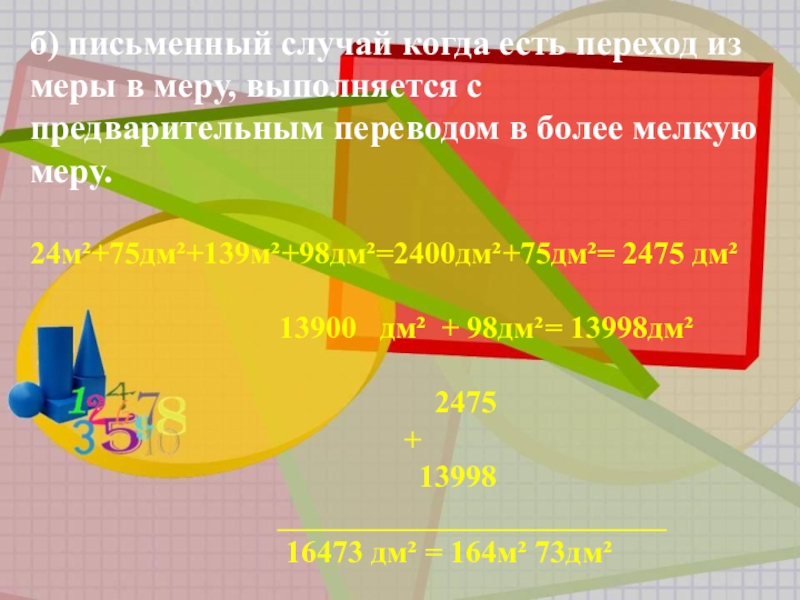
Слайд 28б) письменный случай когда есть переход из меры в меру,
выполняется с предварительным переводом в более мелкую меру.
24м²+75дм²+139м²+98дм²=2400дм²+75дм²= 2475 дм²
13900 дм² + 98дм²= 13998дм²
2475
+
13998
_________________________
16473 дм² = 164м² 73дм²
Слайд 297 этап.
-умножение и деление величины на число
а)устные случаи без перехода
3м² 30 дм² * 3= 9м² 90 дм²
б) письменные случаи с переходом предварительным переводом в мелкую меру
15 м² 60 дм²* 3=1500 дм²+60 дм²
1560 дм² * 3 = 4680 дм²:100=468 м²
Слайд 30Вывод:
Основными целями математического образования являются:
– интеллектуальное развитие учащихся, формирование качеств
мышления, характерных
для математической деятельности и необходимых человеку для полноценной жизни
в
обществе;
– овладение конкретными математическими знаниями, умениями и
навыками, необходимыми для применения в практической деятельности, для изучения
смежных дисциплин, для продолжения образования;
– воспитание личности в процессе освоения математики и математической
деятельности;
– формирование представлений об идеях и методах математики, о математике как
форме описания и методе познания действительности.