Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Финансовые вычисления по простым процентам
Содержание
- 1. Финансовые вычисления по простым процентам
- 2. В практике экономических и финансовых
- 3. Поэтому при принятии решений
- 4. Процент – это всегда конкретное проявление экономической
- 5. При измерении в процентах, процентная ставка показывает,
- 6. Под наращенной суммой ссуды (выданных в долг
- 7. Размер процентной ставки зависит как от объективных
- 8. Следует обратить особое внимание на то, что
- 9. Существует два принципа расчета процентов:наращение на сумму
- 10. Процентные ставки могут быть фиксированными (в контракте
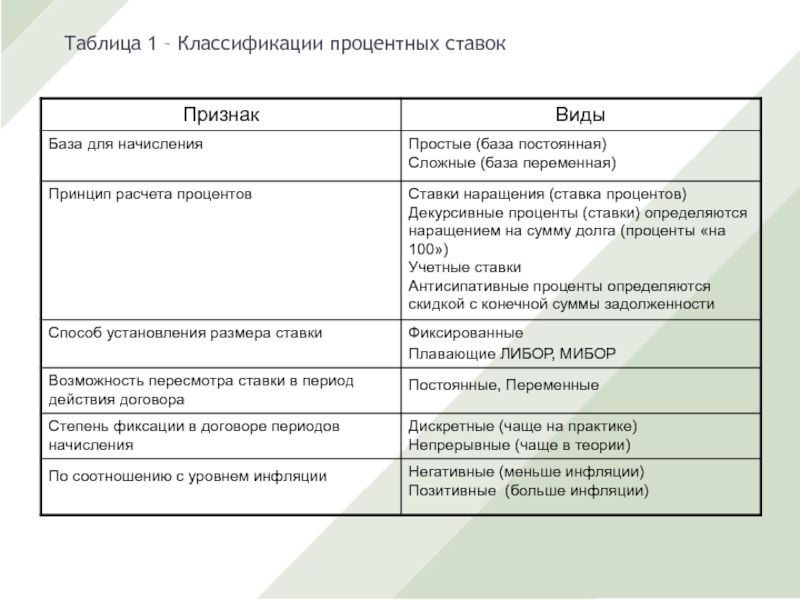
- 11. Таблица 1 – Классификации процентных ставок
- 12. Простые проценты — это метод расчета дохода
- 13. Для записи формулы наращения простых процентов введем
- 14. Слайд 14
- 15. График роста по простым процентам будет иметь
- 16. Слайд 16
- 17. Слайд 17
- 18. В случаях когда срок ссуды меньше периода
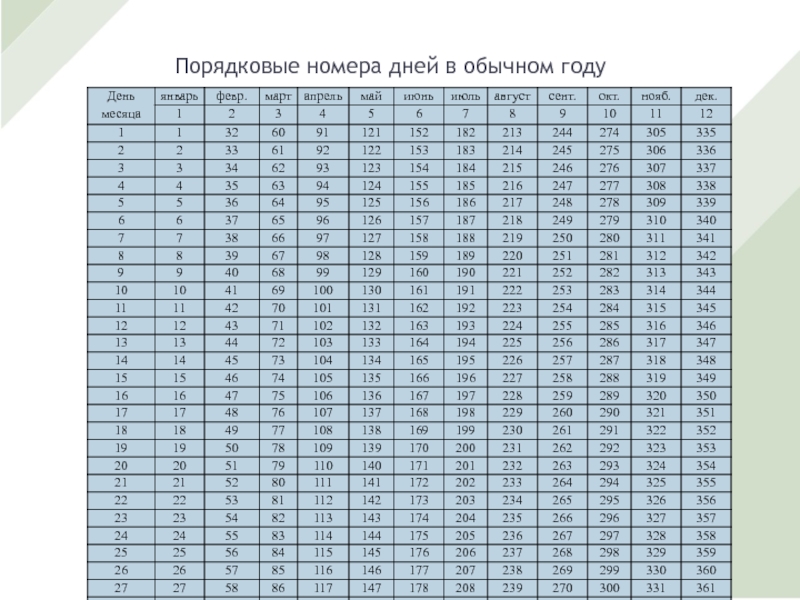
- 19. Порядковые номера дней в обычном году
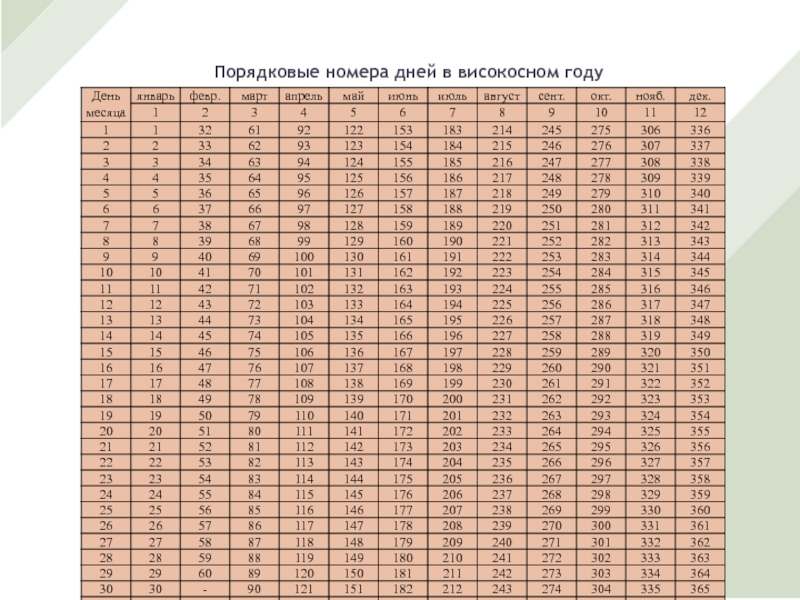
- 20. Порядковые номера дней в високосном году
- 21. При определении числа дней пользования ссудой также
- 22. Таким образом, имеется три практически применяемых варианта
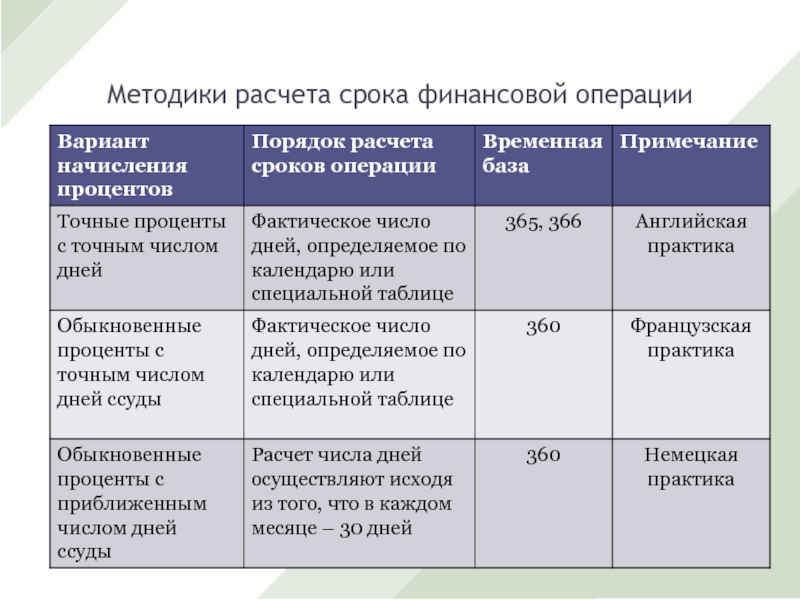
- 23. Методики расчета срока финансовой операции
- 24. Особо следует остановиться на случае, когда начальная
- 25. В мировой практике при расчете процентов используются
- 26. Таким образом, процентный платеж определяется путем деления
- 27. Пример 2 : Капитал величиной 50 млн. руб. вложен
- 28. Начисление процентов при изменении суммы депозита во
- 29. 3. Начисление процентов в смежных календарных периодах
- 30. В кредитных соглашениях иногда предусматриваются изменяющиеся во
- 31. Если известна величина первоначального долга (капитала), то
- 32. Рис. 2. Контур операции
- 33. Юридический факультетФакультет прикладной информатики Кафедра экономической кибернетикиБурда Алексей ГригорьевичСпасибо за внимание
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Факультет прикладной информатики
Кафедра экономической кибернетики
ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ
ПО ПРОСТЫМ ПРОЦЕНТАМ
1. Временной
Слайд 2 В практике экономических и финансовых расчетов суммы денег
обязательно связываются с конкретными моментами или периодами времени. Необходимость учета
временного фактора выражается в принципе неравноценности денег, относящихся к разным моментам времени (time-value of money). 1 млн. руб. сегодня неравноценен 1 млн. руб. через 5 лет. Эта неравноценность двух одинаковых по абсолютной величине сумм связана не только с инфляцией и риском их неполучения. Имеющиеся сегодня деньги теоретически могут быть инвестированы и принести доход в будущем. Полученный доход может быть реинвестирован и т.д. Поэтому сегодняшние деньги ценнее будущих, а будущие поступления менее ценны, чем современные.1. Временной фактор в финансово-экономических расчетах. Основные сведения о процентах.
Факультет прикладной информатики
Слайд 3
Поэтому при принятии решений долгосрочного характера неправомерно
суммировать денежные величины, относящиеся к разным моментам времени.
В то же
время там, где фактор времени не имеет принципиального значения, такое суммирование для получения итогов по периодам допустимо (иногда в бухучете, финансовом контроле).Учет фактора времени осуществляется с помощью начисления процентов и дисконтирования.
Под процентами (процентными деньгами, процентным платежом) понимают абсолютную величину дохода от предоставления денег в долг, т. е. это «цена долга».
Слайд 4 Процент – это всегда конкретное проявление экономической категории «ссудный процент».
Форма долга может быть различной – выдача ссуды, продажа товара
в кредит, помещение денег на депозитный счет, учет векселя, покупка облигаций и т.д. «Цену долга» во всех случаях называют процентом, несмотря на то, что он выражен в абсолютной величине.При заключении финансового или кредитного соглашения кредитор и заемщик договариваются о размере процентной ставки.
Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени, т. е. отношение дохода (процентных денег) к сумме долга за единицу времени.
Процентная ставка может измеряться:
а) в виде натуральной дроби - 1/16 или 1/32,
б) в виде десятичной дроби - 0,075, 0,11 и т.д.,
в) в процентах - 7,5%, 11% и т.д.
Слайд 5 При измерении в процентах, процентная ставка показывает, сколько денежных единиц
должен заплатить заемщик за пользование 100 денежными единицами в определенном периоде
времени.Временной интервал, к которому приурочена процентная ставка, называют периодом начисления. В качестве периода начисления принимают год, квартал, месяц или день.
Начисленные за соответствующие периоды проценты выплачиваются кредитору или присоединяются к основной сумме долга. В последнем случае (когда проценты присоединяются к основной сумме долга) говорят о капитализации процентов.
Процесс увеличения суммы денег в связи с начислением и присоединением процентов называют наращением или ростом первоначальной суммы, иногда - компаудингом.
Слайд 6 Под наращенной суммой ссуды (выданных в долг или инвестированных денег;
долга, депозита) понимают первоначальную ее сумму с начисленными процентами к
концу срока. Наращенная сумма определяется умножением первоначальной суммы долга на множитель наращения.Множитель наращения показывает, во сколько раз наращенная сумма больше первоначальной.
Слайд 7 Размер процентной ставки зависит как от объективных факторов:
общего состояния экономики,
состояния
денежно-кредитного рынка,
вида сделки,
валюты сделки,
срока кредита,
так и от субъективных факторов:
кратковременных и
долгосрочных ожиданий динамики рынка,особенностей заемщика и кредитора,
истории их предыдущих отношений.
Слайд 8 Следует обратить особое внимание на то, что в конечном итоге
на величину процентной ставки, а следовательно, и на процессы наращения
и дисконтирования, оказывает существенное влияние неопределенность и риск. Нетрудно видеть, что перечисленные выше факторы отражают именно эти моменты. Значительная неопределенность и высокий риск действуют как факторы повышения процентных ставок.Процентная ставка применяется не только как инструмент наращения суммы долга, но и в более широком смысле — как измеритель степени доходности (эффективности) любой деятельности независимо от того, имел место или нет факт выдачи денег в долг и процесс наращения этой суммы.
Можно выделить ряд признаков, по которым различаются процентные ставки.
Проценты различаются по базе для их начисления. Если применяется постоянная база используют простые проценты. Если за базу принимается сумма, полученная на предыдущем этапе наращения, т. е. переменная база – используют сложные проценты, т. е., проценты начисляются на проценты.
Слайд 9 Существует два принципа расчета процентов:
наращение на сумму долга — в
этом случае применяют ставку наращения (ставку процентов). Проценты, полученные по
ставке наращения называют декурсивными (в России- проценты «на сто»);скидка с конечной суммы — в этом случае применяют учетные ставки. Проценты, полученные по учетной ставке называют антисипативными (в России – проценты «со ста»);
Слайд 10 Процентные ставки могут быть фиксированными (в контракте указывается их размер)
или «плавающими» (в контракте указывается не сама ставка, а изменяющаяся
во времени база или «базовая ставка» и размер надбавки к ней — маржи. Примером базовой ставки может служить Лондонская межбанковская ставка ЛИБОР, Московская ставка МИБОР.Размер маржи может быть постоянным на протяжении срока ссудной операции или переменным. Постоянными или переменными могут быть и фиксированные процентные ставки.
В практических расчетах чаще применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные в договоре интервалы времени (год, полугодие, месяц) – время рассматривается как дискретная переменная. В некоторых случаях – в формальных доказательствах, в общих теоретических разработках; в финансовых расчетах, связанных с процессами, которые можно рассматривать как непрерывные – возникает необходимость в применении непрерывных процентов. На практике они используются редко.
Слайд 12
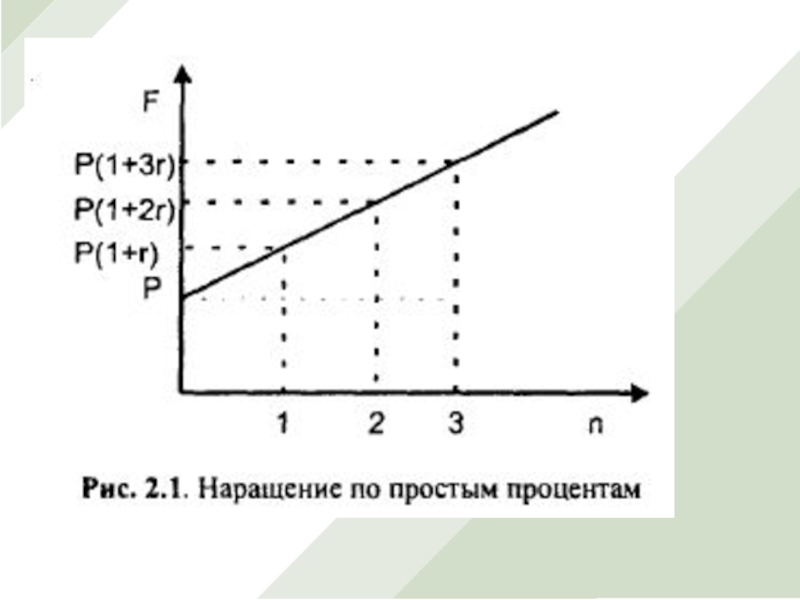
Простые проценты — это метод расчета дохода кредитора от предоставления
денег в долг заемщику. Сущность простых процентов заключается в том,
что они начисляются на одну и ту же постоянную величину капитала в течение всего срока ссуды.На практике этот метод применяется в тех случаях, когда срок ссуды меньше года — месяцы или дни, а также в случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются кредитору.
Сущность и формула простых процентов. Методики расчета сроков финансовой операции
Слайд 13 Для записи формулы наращения простых процентов введем обозначения:
I – проценты
за весь срок ссуды (процентный платеж),
P – первоначальная сумма долга,
S
– наращенная сумма, или сумма в конце срока,i – годовая ставка процентов (ставка наращения в виде десятичной дроби),
n – срок ссуды, лет.
Начисленные проценты за каждый год равны Pi.
Проценты, начисленные за весь срок составят I=Pni
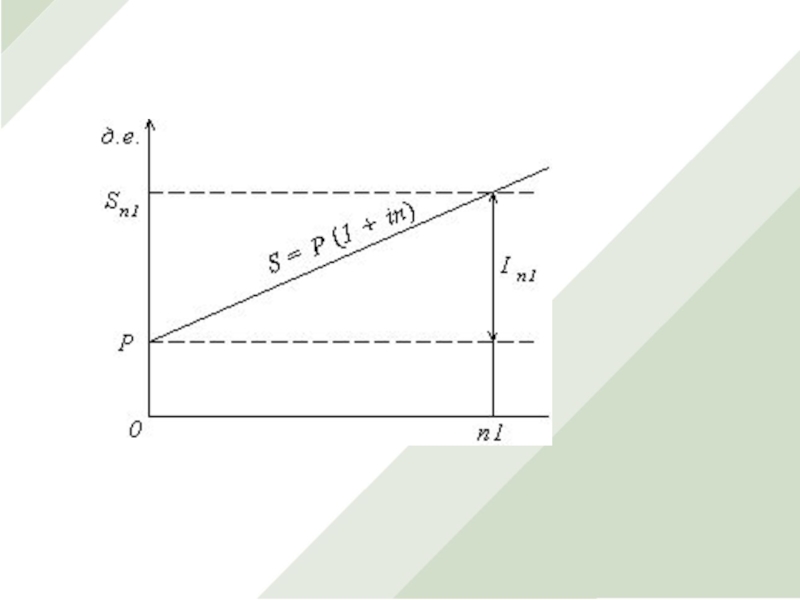
Наращенная сумма находится как S=P+I=P+Pni=P(1+ni).
Формулу S=P(1+ni) называют формулой наращения по простым процентам или кратко — формулой простых процентов.
Множитель (1+ni) называют множителем наращения простых процентов.
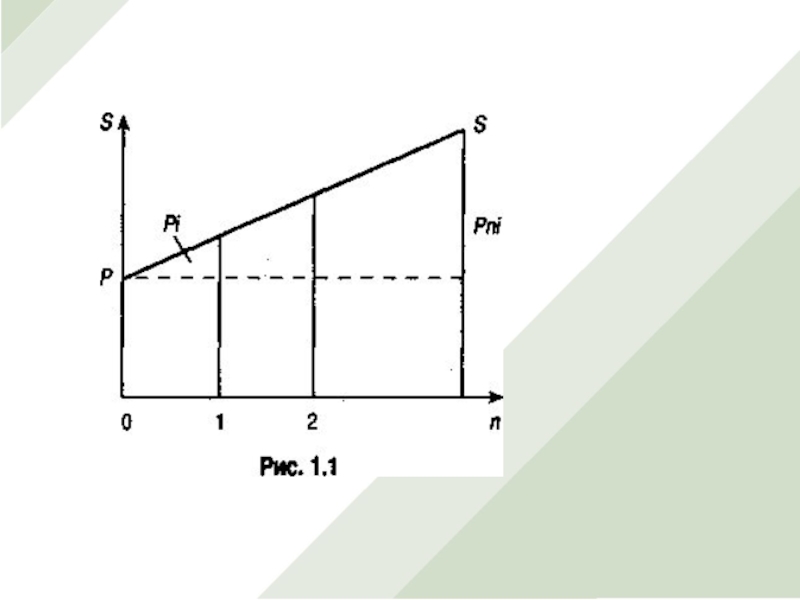
Слайд 15График роста по простым процентам будет иметь вид:
ДЕНЬГИ
S
Pi Pni
P
1 2 n ВРЕМЯ
Рис. 1- График роста по простым процентам
Слайд 18 В случаях когда срок ссуды меньше периода начисления возникает вопрос:
какая часть процента должна быть уплачена кредитору?
Наиболее распространенный в практике
случай – с годовым периодом начисления, т.к. ставка в договоре указывается обычно годовая. Если же срок ссуды меньше года, требуется определить какая часть годового процента уплачивается кредитору.Общий срок ссуды выразим в виде дроби: n = t /k,
где: t – число дней ссуды,
к – число дней в году или временная база.
Если k=360, за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней) и получают обыкновенные или коммерческие проценты.
Если k=365 (366), за базу берут действительное число дней в году (365 или 366), то получают точные проценты.
При одинаковом числе дней ссуды соотношение между точными (Ie) и обыкновенными (Io) процентами будет следующим: Ie / Io = 0,986301= Pit/365 / Pti/360 = 1/365 / 1/360= 360/365
Io / Ie= 1,013889
Слайд 21 При определении числа дней пользования ссудой также применяются два подхода:
-
точный (t),
- приближенный (30).
В первом случае подсчитывается фактическое число дней
между датами, во втором – принимается равным 30 дням.И в том, и в другом случае день выдачи и день погашения считается за один день. Во многих странах первый день не учитывается, а последний учитывается.
Например, если вычисляется число дней с 22 апреля по 16 августа:
в апреле (30-22) = 8
в мае 31
в июне 30
в июле 31
в августе 16
Итого 116
Для подсчета числа дней ссуды можно использовать таблицу порядковых номеров дней в году: 228-112=116 дн., эти таблицы приводятся в справочниках по финансово-экономическим расчетам.
Слайд 22 Таким образом, имеется три практически применяемых варианта оценки:
1. Обыкновенные проценты
с приближенным числом дней ссуды – применяются в Германии, Дании,
Швеции, России (360/360).В России при исчислении процентов количество дней в месяце условно принимается за 30, а в году за 360. В месяцах, имеющих 31 день, 31 число в расчет не принимается, а в феврале остаток за последнее число повторяется столько раз, сколько дней недостает до 30.
2. Обыкновенные проценты с точным числом дней (365/360). Они распространены в операциях коммерческих банков Франции, Бельгии, Испании, Швейцарии, Югославии.
3. Точные проценты с точным числом дней (365/365). Применяются в Португалии, Англии, США, а также при расчетах центрального банка с контрагентами.
Вариант расчета с точными процентами и приближенным числом дней ссуды лишен смысла.
«Где два экономиста, там три мнения»
У.Черчилль: "Если поместить в одну комнату двух экономистов, вы получите два мнения. Но если одним из них окажется Лорд Кейнс, мнений будет три"
Слайд 24 Особо следует остановиться на случае, когда начальная или конечная даты
ссуды приходятся на 31 число месяца, а количество дней ссуды
определяются приближенно, на основе 360 – дневного года. т.е. ссуда, скажем выдается 31 числа, в день, которого при схеме «двенадцать 30-дневных месяцев» не существует, а в реальной действительности сделки могут заключаться и в этот день.При этом возможно использование либо американского, либо европейского метода определения приближенного числа дней ссуды.
Американский метод определения приближенного числа дней ссуды. Если начальная дата является 31-м числом месяца, то она полагается равной 30-ому числу того же месяца. Если конечная дата является 31-числом месяца, а начальная дата меньше, чем 30-число, то конечная дата полагается равной 1-ому числу следующего месяца, в противном случае конечная дата полагается равной 30-ому числу того же месяца.
Европейский метод определения приближенного числа дней ссуды. Начальная и конечная даты, которые приходятся на 31-ое число месяца, полагаются равными 30-ому числу того же месяца.
Слайд 25
В мировой практике при расчете процентов используются понятия «процентное число»
и «процентный ключ» (дивизор).
Определим процентный платеж для t дней
с использованием:А) приближенных процентов В) точных процентов
К = 360 К = 365
I = Pni = Pti / 360 I = Pti / 365
I= Ptix / 36000 I = Ptix / 36500
Разделим в этих формулах числитель и знаменатель на i (ix):
I= Pt / 360/i I= Pt / 365/i
I= Pt / 36000/ix I= Pt / 36500/ix
Числитель Pt в этом выражении называют процентным числом, а
знаменатель - процентным ключом или дивизором.
Слайд 26 Таким образом, процентный платеж определяется путем деления процентного числа на
процентный дивизор.
Понятно, что процентный платеж, вычисляемый с использованием дивизора 365/i
будет меньше, чем процентный платеж, полученный при использовании дивизора 360/i. Поэтому при обслуживании конкретного заемщика всегда используется только один из дивизоров.Пример 1 :
Капитал величиной 10 млн. руб. вложен в банк на 4 месяца под 15% годовых. Найти наращенную сумму:
S = 10 (1+ 4/12 x 0,15) = 10,5 млн. руб. или
I = 10x1200 / 360/0,15 = 1200/2400 = 0,5 млн. руб.
S = 10+0,5 = 10,5
Слайд 27 Пример 2 :
Капитал величиной 50 млн. руб. вложен в банк с
6 марта по 9 июля того же года включительно под 20% годовых. Определить
процентный платеж и наращенную сумму капитала:t = 125дн. – год високосный
t = 23+30+30+30+10 = 123дн. с точным числом
а) точные проценты с точным числом дней ссуды (365/365)
I = 50х125 / 366/0,2 = 6250/1830 = 3,415
S = 53,415
б) обыкновенные проценты с точным числом дней
I = 50x125 / 360/0,2 = 6250/1800 = 3,472
S= 53,472
в) обыкновенные проценты с приближенным числом дней
I= 50x123 / 360/0,2= 6150/1800= 3,416(6)
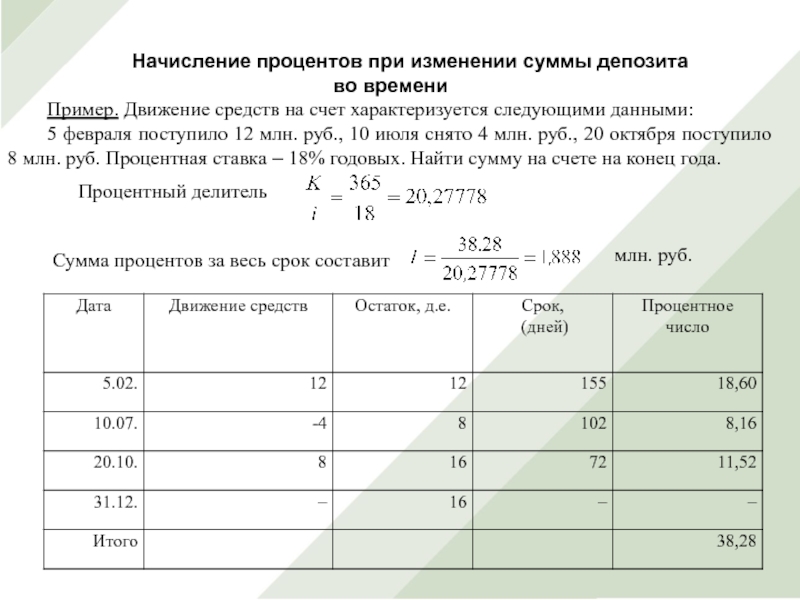
Слайд 28Начисление процентов при изменении суммы депозита
во времени
Пример. Движение средств на
счет характеризуется следующими данными:
5 февраля поступило 12 млн. руб.,
10 июля снято 4 млн. руб., 20 октября поступило 8 млн. руб. Процентная ставка – 18% годовых. Найти сумму на счете на конец года. Сумма процентов за весь срок составит
млн. руб.
Процентный делитель
Слайд 293. Начисление процентов в смежных календарных периодах и при переменных
ставках
Часто даты начала и окончания ссуды находятся в смежных календарных
отрезках времени. Понятно, что начисленные проценты не могут быть целиком отнесены к одному из них.Необходимость деления общей суммы процентов между периодами возникает в бухгалтерском учете, при налогообложении, финансовом анализе деятельности предприятия.
Если общий срок ссуды захватывает два смежных календарных периода, причем на первый приходится срок n1, на второй – n2, то алгоритм деления процентов между смежными календарными периодами:
I= I1 + I2= Pn1i + Pn2i (2)
Слайд 30 В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.
Если
это простые ставки, то наращенная на конец срока сумма определяется
так:формула наращения по простым процентам с переменными ставками.
Слайд 31 Если известна величина первоначального долга (капитала), то для определения процентного
платежа используют расчет «от ста»: I= Pni. Однако при расчете
величины процентного платежа не всегда известен размер первоначальной суммы P; могут быть ситуации, когда известна только величина капитала, уменьшенного или увеличенного на процентный платеж.Если при расчете процентов известна величина капитала, уменьшенного на процентный платеж, то такой расчет называется расчетом «меньше ста».
Если известна величина капитала, увеличенного на процентный платеж, то такой расчет называется расчетом «выше ста».