Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ФИЗИЧЕСКОЕ МАТЕРИАЛОВЕДЕНИЕ Лекция 7 - 8 Т-Х диаграммы фазовых равновесий
Содержание
- 1. ФИЗИЧЕСКОЕ МАТЕРИАЛОВЕДЕНИЕ Лекция 7 - 8 Т-Х диаграммы фазовых равновесий
- 2. Слайд 2
- 3. Точки a и b – фигуративные точки
- 4. Точки А' и В' на ДФР соответствуют
- 5. Количественное соотношение фаз, находящихся в равновесии при
- 6. x
- 7. Задача 5.1. Определить вариантность системы С (рис.
- 8. Слайд 8
- 9. Слайд 9
- 10. Обе фазы - исчезающая в процессе кристаллизации,
- 11. Условия реализации ДФР с неограниченной растворимостьюДвойные системы
- 12. Слайд 12
- 13. Из элементарных алмазоподобных полупроводников диаграмму фазового равновесия
- 14. Применение твердых растворов с неограниченной растворимостьюНеограниченная растворимость
- 15. Твердые растворы с неограниченной растворимостью (металлические и
- 16. Скачать презентанцию
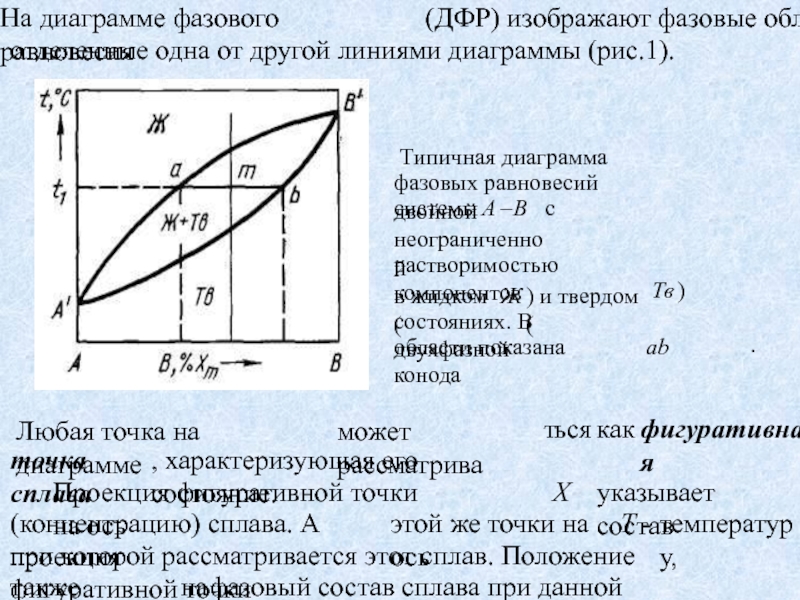
Точки a и b – фигуративные точки фаз, точка m – фигуративная точка сплава. Если фигуративная точка находится в однофазной области, то состав фазы совпадает с составом сплава. Если фигуративная точка
Слайды и текст этой презентации
Слайд 3Точки a и b – фигуративные точки фаз, точка m
– фигуративная точка сплава. Если фигуративная точка находится в однофазной
области, то состав фазы совпадает с составом сплава. Если фигуративная точка находится в пределах двухфазной области, то состав фаз, находящихся в равновесии при данной температуре, определяется с помощью конóды, проходящей через эту точку. Конóдой называется отрезок прямой, проведенной при постоянной температуре (т.е. изотерме) и заключенной в пределах двухфазной области. Конода пересекает границы этой области в точках, лежащих на сопряженных линиях и являющихся фигуративными точками фаз, находящихся в равновесии при данной температуре, т.е. конода соединяет точки, характеризующие составы фаз, находящихся в равновесии. ab – конода.Слайд 4Точки А' и В' на ДФР соответствуют температуре плавления чистых
компонентов двойной системы А и В, соответственно.
Линия А'аВ', выше которой
все сплавы находятся в жидком состоянии, называется линией ликвидуса (L): она представляет собой геометрическое место точек, характеризующих состав жидкой (Ж) фазы (раствора) предельной концентрации и температурную зависимость этой концентрации.Линия А'bВ', ниже которой все сплавы находятся в твердом состоянии, называется линией солидуса (S): она представляет собой геометрическое место точек, характеризующих состав твердой (Тв) фазы (раствора) предельной концентрации и температурную зависимость этой концентрации.
Область между линиями ликвидуса и солидуса – 2-х фазная область сосуществования жидкой и твердой фаз (раствора).
Слайд 5Количественное соотношение фаз, находящихся в равновесии при данной температуре, определяется
с помощью правила рычага: отношение массовых или объемных количеств Q-фаз,
находящихся в равновесии при данной температуре, обратно пропорционально отношению отрезков коноды, заключенных между фигуративной точкой сплава и фигуративными точками соответствующих фаз.Слайд 7Задача 5.1. Определить вариантность системы С (рис. 5.1) для: а)
чистых компонентов А и В при температуре плавления; б) сплавов,
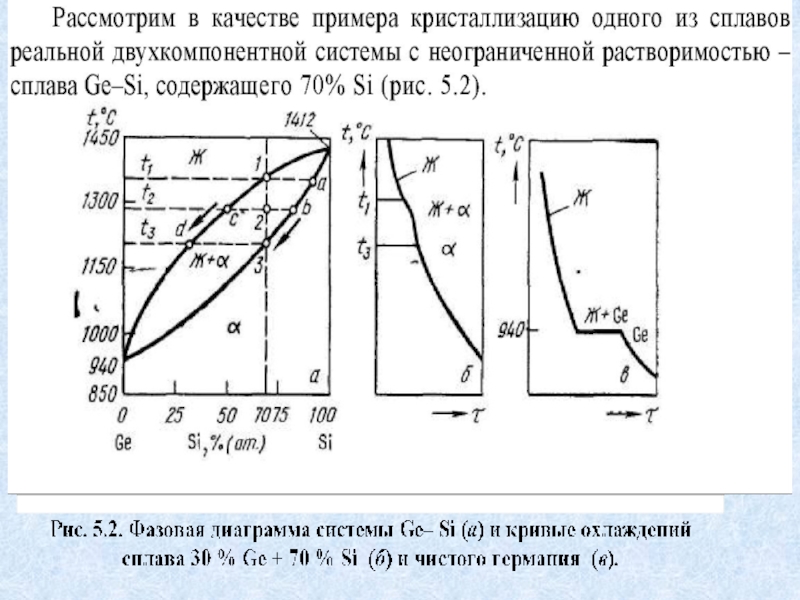
находящихся в однофазных областях (жидкой и твердой); в) сплавов, находящихся в двухфазной области.Слайд 10Обе фазы - исчезающая в процессе кристаллизации, и возникающая -
обогащаются в ходе кристаллизации одним и тем же компонентом, в
рассматриваемом случае - Ge (германием). Это одновременное обогащение одним и тем же компонентом происходит за счет одновременного резкого уменьшения количества фазы, более богатой этим компонентом (в рассматриваемом случае жидкой фазы, более богатой германием). Отметим, что по окончании процесса кристаллизации, прошедшего в равновесных условиях, имеется только твердая фаза, при этом состав ее отвечает составу жидкого раствора (в рассмотренном примере это твердый раствор, содержащий 70 % Si).Слайд 11Условия реализации ДФР с неограниченной растворимостью
Двойные системы А – В,
компоненты А и В которых неограниченно растворяясь друг в друге
в жидком и твердом состоянии, могут быть образованы как химическими элементами, так и соединениями. При этом оба компонента должны:а) обладать одинаковым типом химической связи;
б) обладать одинаковым типом кристаллических решеток;
в) параметры элементарных ячеек (или атомные радиусы) не должны различаться (Δa, ΔR) более чем на (10-15)%;
г) иметь схожий потенциальный рельеф кристаллических решеток компонент.
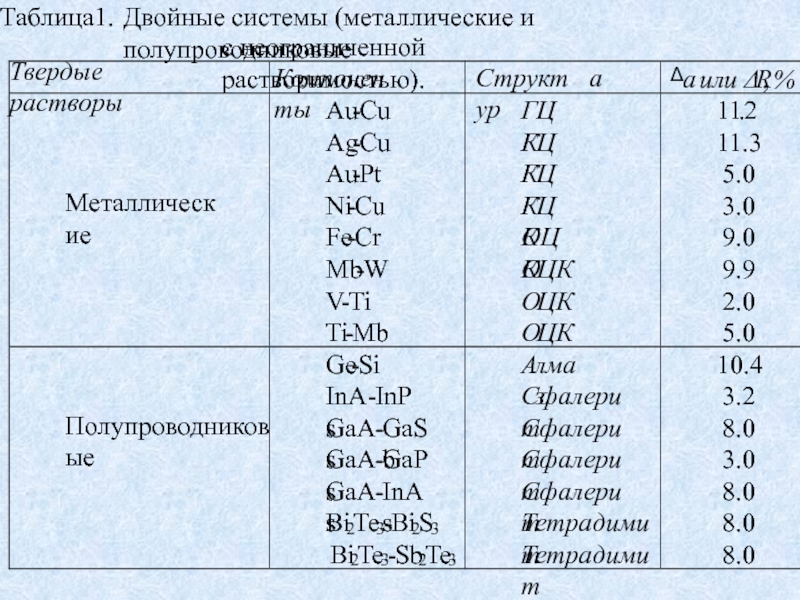
Такие растворы представляют собой изовалентные растворы замещения (табл. 1)
Слайд 13Из элементарных алмазоподобных полупроводников диаграмму фазового равновесия с неограниченной растворимостью
образуют только кремний и германий. Они полностью отвечают перечисленным выше
требованиям. Кремний же и углерод (алмаз) отвечают требованиям по химической природе и типу решетки, но очень сильно различаются по размеру ковалентных тетраэдрических радиусов (RSi = 0,117 нм, RC = 0,077 нм; ΔR/RSi =36 %). В связи с этим растворимость углерода в кремнии не превышает сотых долей процента, а кремния в углероде еще меньше.Слайд 14Применение твердых растворов с неограниченной растворимостью
Неограниченная растворимость - очень распространенное
явление среди полупроводниковых соединений. Их образуют между собой очень многие
соединения классов AIIIВV, AIIBVI, A2VB3VI и др. (см. табл. 1). Такие твердые растворы находят широкое применение. Этому способствует то, что твердые растворы полупроводников, с неограниченной растворимостью позволяют получать сплавы с любыми значениями ширины запрещенной зоны, периода решетки (межатомных расстояний), коэффициентов термического расширения и ряда других параметров в пределах между их значениями для исходных компонентов. Периоды решетки в первом приближении изменяются аддитивно (правило Вегарда), другие параметры - по более сложным законам.Слайд 15Твердые растворы с неограниченной растворимостью (металлические и полупроводниковые) широко применяются:
1.
Au-Cu, Ag-Cu – в контактах приборов;
2. Cu-Ni – в электровакуумных
приборах;3. Fe-Cr – в нержавеющих сплавах;
4. Mb-W, Mb-Ti, V-Ti – тугоплавкие материалы.
5. Полупроводниковые твердые растворы - полупроводниковые термоэлементы, микроэлектроника, оптоэлектроника.
Учитывая возможности, создаваемые твердыми растворами с неограниченной растворимостью, установление зависимостей их свойств от состава является важной материаловедческой задачей.