Физическое материаловедение Молекулярная спектроскопия

характеристики электронных состояний важны:
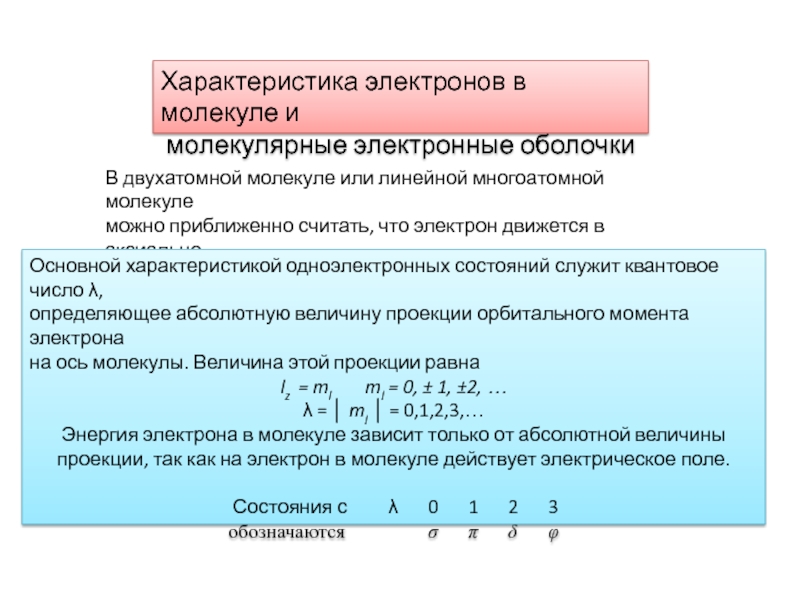
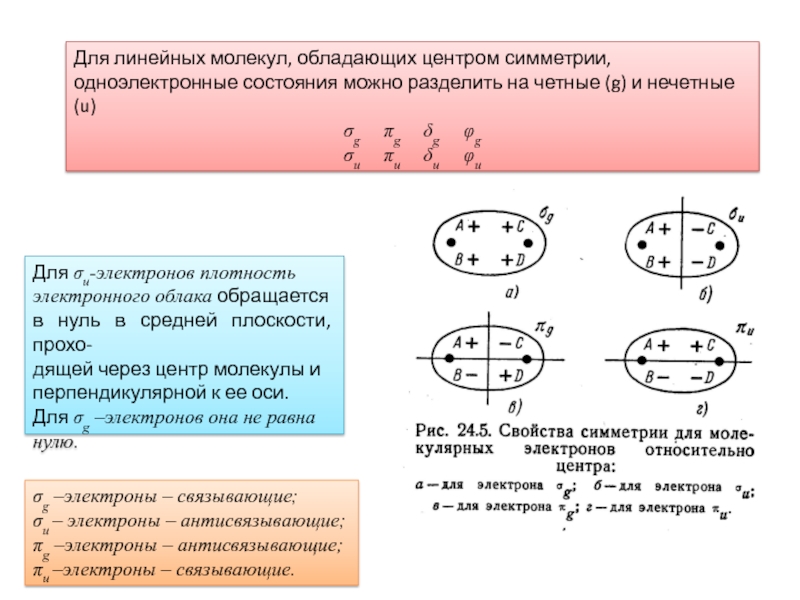
Свойства симметрии;
Зависимость электронной энергии от межъядерного расстояния,

т.е. потенциальные кривые.

Два подхода, использующиеся при характеристике электронных состояний молекул

Рассмотрение состояний молекулы в целом

Определение молекулярных термов из состояний отдельных атомов

прежде всего, наличием аксиальной симметрии – оси симметрии бесконечного порядка

C∞ , проходящей через ядра молекулы. Такой осью обладает любая линейная молекула.

Линейные молекулы могут относиться к 2 точечным группам симметрии 1) C∞v и 2) D ∞h

Молекула обладает осью симметрии C∞ и бесконечным числом плоскостей симметрии σv , проходящих через эту ось. (HCl, CO, NO, CH, HCN, etc.)
Молекула дополнительно обладает центром симметрии i и плоскостью симметрии σh, проходящей через центр симметрии, перепендикулярно к оси молекулы. (H2, N2, O2… C2, H2 и линейные многоатомные молекулы, содержащие пары симметрчно расположенных одинаковых ядер СO2, C2H2, C4H2 etc.)

на квантовании
проекции момента количества движения
Аксиально симметричное электрическое поле действует на

полный орбитальный
момент, вызывая его прецессию вокруг оси поля (молекулы). В результате сохраняется
лишь квантование проекции Lz на ось молекулы
Lz = mL mL = 0, ±1, ±2…
Абсолютную величину проекции полного орбитального момента принято обозначать
Λ = │ mL │ = 0, 1, 2…

Λ = 0 1 2 3 4
Σ Π Δ Φ Γ

В молекуле существуют электростатические и магнитные взаимодействия между электронами, что приводит к векторному сложению моментов количества движения. В отличие от атома, в линейной молекуле имеется не сферически симметричное (как в атоме), а аксиально симметричное электрическое поле.

спиновый момент
1Σ, 1Π … - синглеты
2Σ, 2Π… - дублеты
3Σ, 3Π…

- триплеты

Наряду с квантовым числом Λ важную роль играют характеристики,
связанные с наличием плоскостей симметрии σv и центра симметрии

По отношению к отражению в плоскости симметрии σv ,
проходящей через ось молекулы, электронные состояния разделяются на положительные + и отрицательные –

Для линейных молекул, принадлежащих к группе D ∞h , электронные состояния
делятся на четные и нечетные по отношению к отражению в центре симметрии
Σg+ , Σg-
Σu+ , Σu-

В отличие от полного орбитального момента полный спиновый момент, на который аксиально симметрчное электрическое поле не действует, обычно приближенно сохраняется и квантуется обычным образом.

атома можно представить как молекулу,
на ось которой проектируются моменты

L1 и L2

mL1 = L1, L1 – 1,… – L1
mL2 = L2, L2 – 1,… – L2

Полная проекция равна mL1 + mL2 , а ее абсолютное значение
равно Λ = │ mL1 + mL2 │

При этом Λ принимает значения от 0 до L1 + L2

Σ состояния получаются столько раз , сколько сумма mL1 + mL2
оказывается равной 0

Π состояния получаются столько раз , сколько сумма mL1 + mL2
оказывается равной +1 и –1

спин молекулы S = S1 + S2. При этом возможные

значения спинового квантового числа молекулы будут S = S1 + S2., S1 + S2. – 1, │S1 - S2│, и мультиплетность χ состояния молекулы будет принимать значения
χ = χ1 + χ2 – 1, χ1 + χ2 – 3, … │ χ1 - χ2 │ +1

то
Состояния молекулы будут

S + S Σg+ при

χ = 1,5 Σu+ при χ = 3,7

P + P Σg+ , Σg+ , Σu-, Πg, Πu, Δg Σu+ , Σu+ , Σg-, Πg, Πu, Δu
при χ = 1,5 при χ = 3,7

H2

Два атома водорода в состоянии 2S
образуют молекулу в состояниях χ = 1,3
1Σg+ , 3Σu+

S1+S2-1, … |S1-S2|
χ= χ1+ χ2-1, χ1+ χ2-3…| χ1- χ2|+1
при χ

= 1,3,5,7

1Σg+ 3Σu+ 5Σg+ 7Σu+

N2

или линейной многоатомной молекуле
можно приближенно считать, что электрон движется

в аксиально
симметричном поле ядер и остальных электронов.

Основной характеристикой одноэлектронных состояний служит квантовое число λ,
определяющее абсолютную величину проекции орбитального момента электрона
на ось молекулы. Величина этой проекции равна
lz = ml ml = 0, ± 1, ±2, …
λ = │ ml │ = 0,1,2,3,…
Энергия электрона в молекуле зависит только от абсолютной величины проекции, так как на электрон в молекуле действует электрическое поле.

Состояния с λ 0 1 2 3
обозначаются σ π δ φ

в одинаковых
квантовых состояниях. σ-электроны могут отличаться величиной проекции спина
на

ось молекулы (ms = ½ и ms = - ½ ). Молекулярная оболочка σ2 заполнена
2 электронами. π –электроны могут отличаться знаком проекции орбитального
момента и знаком проекции спина на ось молекулы (ml=λ, ms=1/2; ml=λ, ms=-1/2;
ml=-λ, ms=1/2; ml=-λ, ms=-1/2). Молекулярная оболочка π4 может быть заполнена 4
электронами. Сначала заполняется σ оболочка, а затем π.

на четные (g) и нечетные (u)
σg πg δg φg
σu πu δu φu

Для σu-электронов плотность
электронного облака обращается

в нуль в средней плоскости, прохо-
дящей через центр молекулы и
перпендикулярной к ее оси.
Для σg –электронов она не равна
нулю.

σg –электроны – связывающие;
σu – электроны – антисвязывающие;
πg –электроны – антисвязывающие;
πu –электроны – связывающие.

= 4,48 eV
Распределение зарядовой плотности в молекуле He2
Распределение зарядовой плотности

связь
4 электрона в связывающих орбиталях, 2 электрона – в антисвязывающих
De

= 1,14 эВ

Молекула лития

Chemistry: The Central Science, Eleventh Edition, by Theodore E. Brown, H. Eugene LeMay, and Bruce E. Bursten, Catherine Murphy, and Patrick Woodward.
Published by Prentice Hall.

пар разрыхляющих электронов 2
Энергия диссоциации 5,082 эВ
Молекула кислорода

атом Li является донором, а H акцептором; HF – атом

H донор, а F акцептор.

заданием
для каждого вида эквивалентных электронов их числа ki и

квантового
числа λ
(aσ)k1 (bσ)k2 (cπ)k3 …

Для заданной конфигурации молекулы можно найти значения Λ и S
определить мультиплетные термы
Λ = │±λ1 ±λ2 ±λ3│
Сложение спиновых моментов si дает целый или полуцелый спин

В случае неэквивалентных электронов принцип Паули автоматически удовлетворяется, в случае эквивалентных электронов его нужно учитывать.

Λ = │λ1 - λ2│
При λ1 = λ2 = λ,

Λ = λ1 + λ2 =2 λ и два состояния с Λ = 0 (Σ состояния:
Σ+ и Σ-)
Для заполненной оболочки результирующее состояние 1Σ+

Москва, 1962.
Г. Герцберг Спектры и строение двухатомных молекул,

Издательство иностранной литературы, Москва, 1949.
Н.Ф. Степанов Химическая связь в простых двухатомных молекулах, Химия, Соросовский образовательный журнал №10, 1998, с. 37