Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ФИЗИКА
Содержание
- 1. ФИЗИКА
- 2. ЛЕКЦИЯ 1
- 3. ФИЗИКАФизика - наука изучающая
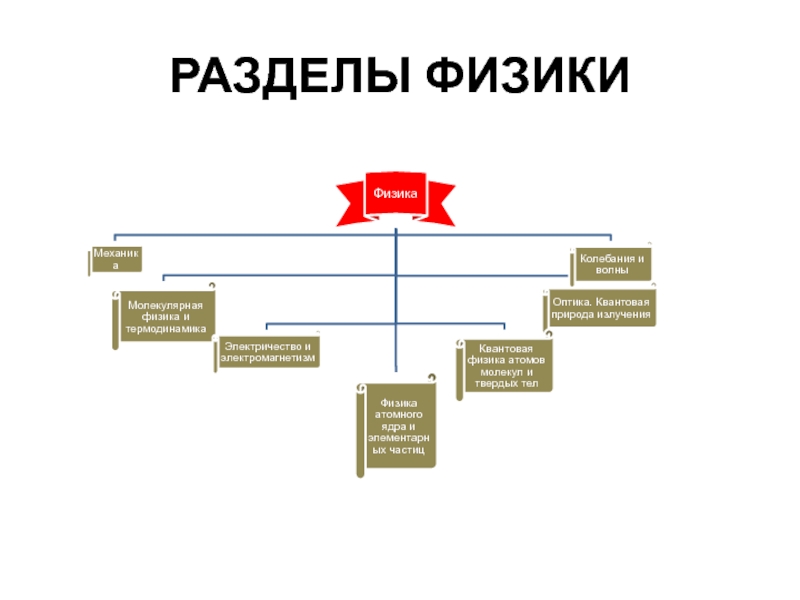
- 4. РАЗДЕЛЫ ФИЗИКИ
- 5. МЕХАНИКАЧасть физики которая изучает зако-номерности механического движе-ния и причины вызывающие или изменяющие это движение.
- 6. МЕХАНИКА – Часть физики которая изучает закономерности
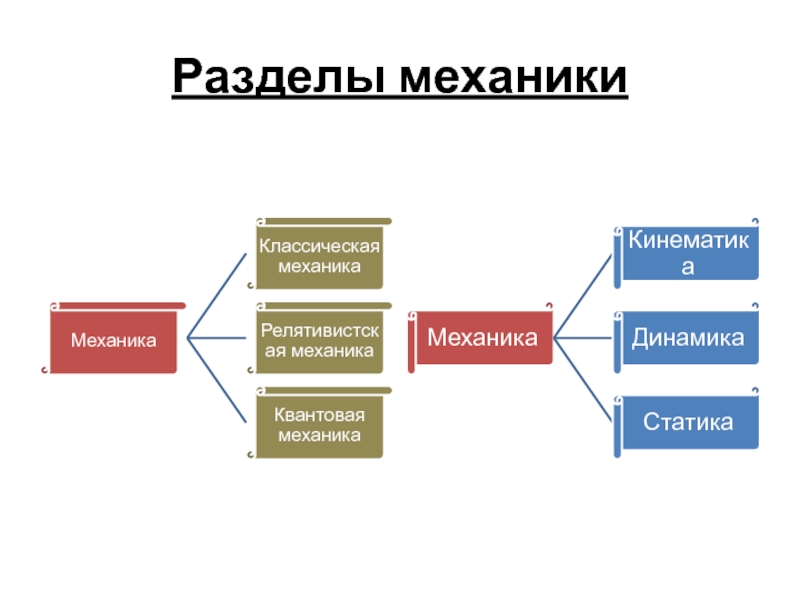
- 7. Разделы механики
- 8. Классическая механика – (механика Галилея-Ньютона) изучает законы
- 9. Кинематика – изучается движение тел не раскрывая
- 10. КИНЕМАТИКА
- 11. ФИЗИЧЕСКИЕ МОДЕЛИМатериальная точка- тело обладающее массой, размерами
- 12. ДВИЖЕНИЕПоступательное движение- движение при котором любая прямая,
- 13. Кинематика поступательного движения
- 14. Кинематические уравнения материальной точкиПоложение матери-альной точки (тела)
- 15. Траектория материальной точкиТраектория материальной точки- линия описываемая
- 16. СкоростьСкорость-величина которой определяется как быстрота движения, так
- 17. Мгновенная скорость –векторная величина, равная первой производной
- 18. УскорениеУскорение- Величина характери-зующая быстроту изменения скорости по
- 19. Мгновенное ускорение- (ускорение матери-альной точки в момент
- 20. Нормальная составляющая ускорения- характеризует быстроту изменения скорос-ти
- 21. Типы движения в зависимости от ускоренияПрямолинейное равномерное движениеПрямолинейное равнопеременное движение
- 22. Прямолинейное движение с переменным ускорениемРавномерное движение по
- 23. Равномерное криволинейное движениеРавнопеременное криволинейное движениеКриволинейное движение с переменным ускорением
- 24. Кинематика вращательного движения
- 25. Угол поворотаПусть некоторая точка движется вокруг своей
- 26. Угловая скоростьУгловая скорость - векторная величина, равная
- 27. Скорость поступательного движения можно выразить через угловую
- 28. Период вращения Т- время за которое совершается
- 29. Угловое ускорениеУгловое ускорение- векторная величина равная первой
- 30. Связь между линейными и угловыми величинамиТангенциальная составляющая ускоренияНормальная составляющая ускоренияСвязь между линейными и угловыми величинами
- 31. Динамика материальной точки и поступательного движения твердого
- 32. Первый закон Ньютона (закон инерции) Всякая материальная точка
- 33. ИНЕРТНОСТЬ, МАССА, СИЛАИнертность- стремление тела сохранить своё
- 34. Масса- физическая величина, являющаяся од-ной из характеристик
- 35. Второй закон Ньютона (основной закон динамики поступательного
- 36. Импульс Импульс (количество движения)-векторная величина численно равная
- 37. Второй закон Ньютона справедлив только в инерциальных
- 38. Принцип независимости действия силЕсли на материальную точку
- 39. Третий закон Ньютона Всякое действие материальных точек (тел)
- 40. -сила действующая на первую материальную
- 41. Законы Кеплера. Закон всемирного тяготения. Сила тяжести. Вес.
- 42. Законы движения планетКаждая планета движется по эллипсу,
- 43. Закон всемирного тяготения Между любыми двумя материальными точ-ками
- 44. Гравитационная постояннаяСмысл гравитационной постоянной G:
- 45. Сила тяжести На любое тело массой m ,
- 46. Абсолютное значение силы тяжестигде: Масса Земли:
- 47. Обобщенный закон Галилея Все тела в одном и
- 48. Вес телаВес тела- сила с которой тело
- 49. Сила тяжести действует ВСЕГДА, вес появляется только
- 50. Виды трения
- 51. Трение внешнее (сухое)-возникает в области касания двух
- 52. Внешнее трение Сила трения скольжения пропорционально силе нормального
- 53. Сила трения скольжения Если тело находится на на-клонной
- 54. Для трения скольжения на гладких поверхностях опреде-лённую
- 55. Закон сохранения импульса
- 56. Механическая система-совокупность матери-альных точек (тел) рассматриваемых как
- 57. Система состоит из n тел у которых соответственно:Массы:Скорости:Равнодействующие внут-ренних силРавнодействующие внеш-них силПо 3 закону Ньютона
- 58. Так как по 3 закону Ньютона геометрическая
- 59. Закон сохранения импульса Импульс замкнутой системы не изменяется
- 60. Центр массВ механике Галилея-Ньютона импульс сис-темы, из-за
- 61. Радиус-вектор центра масс:Где: -масса и радиус
- 62. Закон движения центра массЦентр масс системы двигается
- 63. Движение тел переменной массыВ начальный момент времени
- 64. Изменение импульса системы за время dt:Если на
- 65. Уравнение движения тела переменной массы
- 66. Формула ЦиолковскогоФормула Циолковского показывает:Чем больше конечная масса
- 67. РАБОТА И ЭНЕРГИЯ
- 68. Энергия Энергия – универсальная мера различных форм
- 69. Изменение механического движения тела вызывается силами, действующими
- 70. Работа силы Если тело движется прямолинейно и
- 71. Элементарной работой силы на перемещении
- 72. Для вычисления этого интеграла надо знать за-висимость
- 73. Мощность Что бы охарактеризовать скорость соверше-ния работы вводят
- 74. Кинетическая и потенциальная энергии
- 75. Кинетическая энергия механической системы – энергия механического
- 76. Тело массой m двигающееся со скоростью v
- 77. Стационарные силовые поля называются потен-циальными а силы
- 78. Потенциальная энергия механической системы-механическая энергия системы тел,
- 79. Работа консервативных сил при элементарном из-менении конфигурации
- 80. Виды потенциальной энергииПотенциальная энергия тела массой m
- 81. Потенциальная энергия упругодеформированного тела (пружины): Сила упругости пропорциональна
- 82. Полная механическая энергия системы Полная механическая энергия системы
- 83. Закон сохранения энергии Закон сохранения энергии- результат обоб-щения
- 84. Пусть имеется система состоящая из n материаль-ных
- 85. Так как двигаясь под действием сил, точки
- 86. Сложим уравнения системы и получим:Первый член левой
- 87. Правая часть равенства задаёт работу внешних неконсервативных
- 88. Закон сохранения механической энергии В системе тел между
- 89. Механические системы в которых действуют толь-ко консервативные
- 90. Энергия никогда не исчезает и не появляется
- 91. Скачать презентанцию
Слайды и текст этой презентации
Слайд 5МЕХАНИКА
Часть физики которая изучает зако-номерности механического движе-ния и причины вызывающие
или изменяющие это движение.
Слайд 6МЕХАНИКА – Часть физики которая изучает закономерности механического движения и
причины вызывающие или изменяющие это движение.
МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ – изменение с
течением времени взаимного расположе-ния тел или их частей.Слайд 8Классическая механика – (механика Галилея-Ньютона) изучает законы движения макро-скопических тел,
скорости которых малы по сравнению со скоростью света (с=3*10⁸ м/с)
Релятивистская
механика – основана на специальной теории относительности (СТО), изучает законы движения макроскопических тел со скоростями сопоставимыми со скоростью светаКвантовая механика – служит для описания движения микроскопических тел (отдельных атомов и элементарных частиц) для которых не применимы законы классической механики
Слайд 9Кинематика – изучается движение тел не раскрывая причины по которым
это движение происходит.
Динамика – изучаются законы движения тел и причины,
которые вызывают или изменяют это движение.Статика – изучаются законы равновесия системы тел (отдельно от динамики не рас-сматривается, так как из законов движения можно вывести законы равновесия).
Слайд 11ФИЗИЧЕСКИЕ МОДЕЛИ
Материальная точка- тело обладающее массой, размерами которого в данной
задаче можно пренебречь.
Макроскопическое тело (система тел)- тело (систе-ма тел) которое
можно разбить на малые взаимо-действующие между собой части, каждая из кото-рых может рассматриваться как материальная точка.Абсолютно твёрдое тело- тело, которое не при ка-ких условиях не может деформироваться , и рассто-яние между двумя точками этого тела всегда посто-янно.
Слайд 12ДВИЖЕНИЕ
Поступательное движение- движение при котором любая прямая, жестко связанная с
движущимся телом, остается параллельной своему первоначальному положению.
Вращательное движение- движение при
котором все точки тела движутся по окружностям, центры которой лежат на одной оси.Слайд 14Кинематические уравнения материальной точки
Положение матери-альной точки (тела) определяется по отно-шению
к какому либо другому, произвольно выбранному телу- телу отсчета. С
ним связана система отсчета: совокупность системы координат и часов с телом отсчета.Число независимых ко-ординат- число степеней свободы
Слайд 15Траектория материальной точки
Траектория материальной точки- линия описываемая этой точкой в
пространстве.
Длина пути-ΔS=ΔS(t)-длина учас-тка траектории АВ пройденной точкой с момента начала
отсчета времени (величина скалярная).Перемещение-приращение радиуса вектора точки за время Δt
При прямолинейном движении модуль перемещения равен пройденному пути Ι Ι=ΔS
Слайд 16Скорость
Скорость-величина которой определяется как быстрота движения, так и его направление
в данный момент времени.
Вектор средней скорости
- отношение прира-щения радиуса-вектора точки к промежутку времени Δt. Направление вектора средней скорости совпадает с направлением радиус вектора При Δt→0 средняя скорость стремится к предельному значению, называемому мгновенной скоростью.
Слайд 17Мгновенная скорость –векторная величина, равная первой производной радиуса вектора движущейся
точки во времени. Направлен по касательной к траектории движения
По мере
уменьшения Δt путь ΔS будет приближаться к , то естьΔS
А
В
Слайд 18Ускорение
Ускорение- Величина характери-зующая быстроту изменения скорости по модулю и направ-лению
в случае неравномерного движения.
Среднее ускорение- векторная величина равная отношению изменения
скорости к интервалу времени . -полное ускорение
-тангенциальное ускорение
-нормальное ускоре-ние
Слайд 19Мгновенное ускорение- (ускорение матери-альной точки в момент времени t), предел
среднего ускорения при .(первая производная
скорости по времени).Тангенциальная составляющая ускорения- равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю. Направление- по касательной к траектории движения.
Слайд 20Нормальная составляющая ускорения- характеризует быстроту изменения скорос-ти по направлению, и
направлена по нор-мали к траектории к центру её кривизны.
Полное ускорение
тела- геометрическая сумма тангенциальных и нормальных составляющихСлайд 21Типы движения в зависимости от ускорения
Прямолинейное равномерное движение
Прямолинейное равнопеременное
движение
Слайд 22Прямолинейное движение с переменным ускорением
Равномерное движение по окружности
(При
скорость не изменяется по модулю, а изменяется
по направлению) r-постоянный радиус кривизны.Слайд 23Равномерное криволинейное движение
Равнопеременное криволинейное движение
Криволинейное движение с переменным ускорением
Слайд 25Угол поворота
Пусть некоторая точка движется вокруг своей оси по окружности
радиусом R. Её положение через про-межуток времени Δt за-дадим углом
. Элементарные (бесконечно малые) углы поворота рас-сматривают как векторы, модули которых равны углу поворота.Направление вектора определяется при по-мощи правила право-го винта (буравчика).
R
R
dϕ
dS
Слайд 26Угловая скорость
Угловая скорость - векторная величина, равная первой производной угла
поворота по времени. Вектор нап- равлен
вдоль оси вращения по правилу правого винта.R
Слайд 27Скорость поступательного движения можно выразить через угловую скорость
В векторном виде
В скалярном виде
Если ω=const,
вращательное движение мож-но охарактеризовать периодом вращения ТСлайд 28Период вращения Т- время за которое совершается полный оборот (прохождение
точкой угла 2π)
Частота вращения n- число полных оборо-тов совершаемых телом
при равномерном его движении по окружности в единицу времениСлайд 29Угловое ускорение
Угловое ускорение- векторная величина равная первой произ-водной угловой скорости
по времени. При ускоренном дви-жении сонаправлен вектору
.При замедленном движении направлен в сторону противо-положную .
Слайд 30Связь между линейными и угловыми величинами
Тангенциальная составляющая ускорения
Нормальная составляющая ускорения
Связь
между линейными и угловыми величинами
Слайд 31Динамика материальной точки и поступательного движения твердого тела
Динамика- основной раздел
механики, в её основе лежат 3 закона Ньютона (1687 г.),
рассматриваемые как система взаимосвязанных законов.Слайд 32Первый закон Ньютона
(закон инерции)
Всякая материальная точка (тело) сохраняет состояние покоя
или равномерного прямо-линейного движения до тех пор, пока воз-действие со
стороны других тел не заставит её изменить это состояние.Слайд 33ИНЕРТНОСТЬ, МАССА, СИЛА
Инертность- стремление тела сохранить своё состояние покоя или
равномерного прямо- линейного движения (1 закон Ньютона назы-вают закон инерции
).Инерциальные система отсчёта- система ко-торая либо покоится, либо движется прямо-линейно и равномерно относительно какой- либо другой инерциальной системы отсчёта. 1 закон Ньютона выполняется не в каждой, а только в инерциальных системах отсчёта.
Слайд 34Масса- физическая величина, являющаяся од-ной из характеристик материи, определяющая её
инерционные и гравитационные свойства.
Сила – векторная величина, являющаяся ме-рой механического
воздействия на тело, со стороны других тел и полей, в результате которого тело приобретает ускорение или из-меняет свою форму и размеры. В каждый мо-мент времени сила характеризуется числовым значением направлением в пространстве и точкой приложения. Единица измерения силы Ньютон (Н): 1Н=1 кг*м/с²
Слайд 35Второй закон Ньютона
(основной закон динамики поступательного движения)
Ускорение приобретаемое материальной точкой
(телом) пропорционально вызыва-ющей его силе, совпадает с ней по направ-лению
и обратно пропорционально массе материальной точки (тела).Слайд 36Импульс
Импульс (количество движения)-векторная величина численно равная произведению мас-сы материальной
точки на её скорость и имею-щая направление скорости.
Общая формулировка
второго закона Ньютона:Скорость изменения импульса равна дейст-вующей на него силе
Слайд 37Второй закон Ньютона справедлив только в инерциальных системах отсчета.
Первый закон
Ньютона можно вывести из второго закона Ньютона
. Одна-ко, первый закон Ньютона самостоятельный закон, а не следствие второго закона Ньюто-на, т. к. именно он подтверждает существова-ние инерциальных систем отсчёта, только в которых возможно равенствоСлайд 38Принцип независимости действия сил
Если на материальную точку действует одновременно несколько
сил, каждая из этих сил сообщает материальной точке ускорение согласно
2 закону Нью- тона, как будто других сил не было.Если на материальную точку действует одновременно несколько сил, то по принципу независимости, то под силой действующей на тело понимают результирую-щую силу.
Силы и ускорения можно разлагать на составляющие. Например сила может быть разложена на нормаль-ную и тангенциальную составляющие :
Слайд 39Третий закон Ньютона
Всякое действие материальных точек (тел) друг на друга
носит характер взаимодей-ствия , силы с которыми действуют друг на
друга материальные точки всегда равны по модулю, противоположно направлены и действуют вдоль прямой соединяющей эти точки.Слайд 40 -сила действующая на первую материальную точку со стороны
второй, а на вторую точку со стороны
первой.Силы и приложены к разным материальным точкам (телам), всегда действуют парами, и являются силами одной природы.
Во 2 законе Ньютона речь идёт об ускорении приоб-ретаемом телом под действием приложенных к нему сил. Ускорение равно 0 если равна 0 равнодействую-щая всех сил приложенных к ОДНОМУ ! телу. 3 закон Ньютона говорит о равенстве сил приложенных к РАЗНЫМ ! телам. На каждое тело действует ОДНА сила.
3 закон Ньютона позволяет перейти от динамики одной материальной точки к динамике системы мат. точек.
Слайд 42Законы движения планет
Каждая планета движется по эллипсу, в од-ном из
фокусов которого находится Солнце.
Радиус-вектор планеты за равные проме-жутки времени описывает
равные площади.Квадраты периодов обращения планет вок-руг Солнца относятся как кубы больших осей их полуорбит.
Законы выведены Кеплером, на основе запи-сей Т. Браге. Впоследствии Ньютон на осно- вании законов Кеплера и основных законов динамики вывел:
Слайд 43Закон всемирного тяготения
Между любыми двумя материальными точ-ками действует сила взаимного
притяжения прямо пропорциональная произведению масс и
этих точек, и обратно пропор-циональная квадрату расстояния между ними.(сила всемирного тяготения)
Слайд 44Гравитационная постоянная
Смысл гравитационной постоянной G:
Два тела массами
m₁=m₂=1 кг на расстоя-нии r=1 м, притягиваются друг к другу
с си-лой F=6,6720*10¯¹¹ Н.Слайд 45Сила тяжести
На любое тело массой m , вблизи Земли действует
сила тяготения F под влиянием которой тело будет двигаться с
ускорением свободного падения g=9,8 м/с². Таким обра-зом, на всякое тело m действует сила тяжестиСлайд 46Абсолютное значение силы тяжести
где:
Масса Земли:
кг.
Радиус Земли
(на экваторе): км.При удалении от поверхности Земли на высоту h сила тяжести уменьшается
Слайд 47Обобщенный закон Галилея
Все тела в одном и том же поле
тяготения падают с одинаковым ускорением.
(ускорение незначительно варьируется от радиуса Земли)
Слайд 48Вес тела
Вес тела- сила с которой тело вследствие тя-готения к
Земле действует на опору или под-вес удерживающий от свободного падения.
Вес
тела проявляется только в том случае ес- ли тело двигается с ускорением отличным от g т.е. когда на тело действуют и другие силы.Если тело двигается только под действием силы тяжести оно в состоянии невесомости.
Слайд 49Сила тяжести действует ВСЕГДА, вес появляется только в том случае,
когда на тело кроме силы тяжести действуют и ДРУГИЕ силы
Тело
двигается с ускорением a отличным от g. Если тело двигается в поле тяготения Земли с ускорениемто к телу приложена дополнительная сила удовлетворяющая условию
Тогда вес тела
Если тело покоится или двигается прямолинейно и равномерно и .
Если тело свободно двигается в любом направлении по любой траектории то и т.е. тело будет невесомым.
Слайд 51Трение внешнее (сухое)-возникает в области касания двух соприкасающихся тел при
их относительном пере-мещении. Если соприкасающиеся тела неподвижны- трение покоя. Если
происходит относительное переме-щение этих тел, то в зависимости от характера их отно-сительного движения- трение скольжения, качения .Трение внутреннее- трение между частями одного и то-го же тела, например между слоями жидкости или газа, скорости которых меняются от слоя к слою. В данном случае отсутствует трение покоя.
Если тела скользят относительно друг друга и разделе-ны прослойкой вязкой жидкости –граничное трение (толщина смазки ˂= 1 мкм) или гидродинамическое трение (толстый слой смазки).
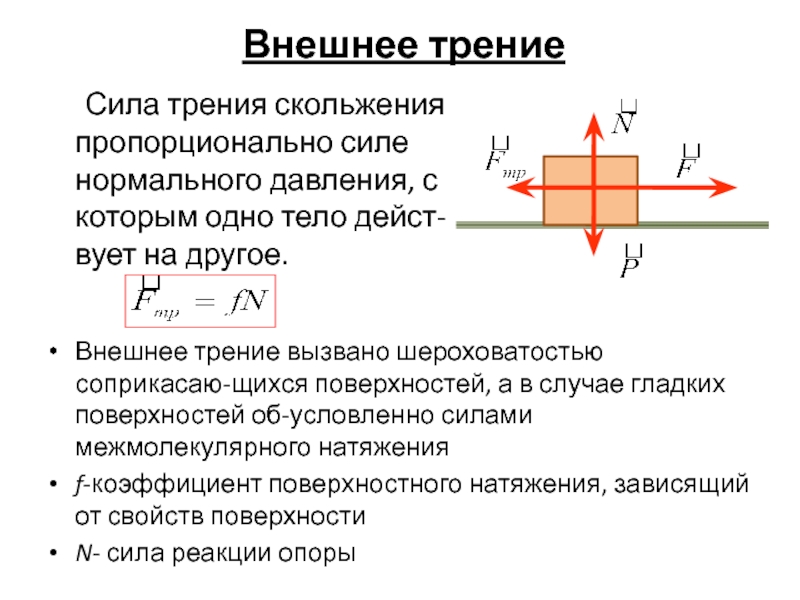
Слайд 52Внешнее трение
Сила трения скольжения пропорционально силе нормального давления, с которым
одно тело дейст-вует на другое.
Внешнее трение вызвано шероховатостью соприкасаю-щихся поверхностей,
а в случае гладких поверхностей об-условленно силами межмолекулярного натяженияf-коэффициент поверхностного натяжения, зависящий от свойств поверхности
N- сила реакции опоры
Слайд 53Сила трения скольжения
Если тело находится на на-клонной поверхности с углом
наклона , то оно приходит в движение, только
когда тан-генциальная составляющая силы тяжести больше силы трения .Для предельного случая (начала скольжения) должно вы-полняться условие:
Из этого следует:
Коэффициент трения равен тангенсу угла α, при котором начинается скольжение по наклону.
Слайд 54Для трения скольжения на гладких поверхностях опреде-лённую роль играет межмолекулярное
притяжение.
Закон трения скольжения (предложен Б.В. Дерябиным)
где:
-истинный коэффициент трения скольжения -площадь контакта между телами
-добавочное давление обусловленное силами межмоле-кулярного притяжения
Сила трения качения (по закону Кулона)
где:
-коэффициент трения качения
-радиус катящегося тела
Слайд 56Механическая система-совокупность матери-альных точек (тел) рассматриваемых как единое целое.
Внутренние силы-
силы взаимодействия меж-ду материальными точками механической системы.
Внешние силы- силы с
которыми на матери-альные точки системы действуют внешние тела.Замкнутая система- система на которую не действуют внешние силы, или геометрическая сумма всех внешних сил равна нулю.
Слайд 57Система состоит из n тел у которых соответственно:
Массы:
Скорости:
Равнодействующие внут-ренних сил
Равнодействующие
внеш-них сил
По 3 закону Ньютона
Слайд 58 Так как по 3 закону Ньютона геометрическая сумма внут-ренних сил
равна нулю
то:где: -импульс системы.
Производная по времени импульса механической систе-мы равна геометрической сумме внешних сил действую-щих на систему.
В случае отсутствия внешних сил (система замкнутая)
Слайд 59Закон сохранения импульса
Импульс замкнутой системы не изменяется с течением времени.
Данный
закон справедлив не только для клас-сической механики, он носит универсаль-ный
характер, то есть он: УНИВЕРСАЛЬНЫЙ ЗАКОН ПРИРОДЫ.Слайд 60Центр масс
В механике Галилея-Ньютона импульс сис-темы, из-за независимости массы от
ско-рости может быть выражен через скорость её центра масс.
Центром масс
(центром инерции)- для сис-темы материальных точек называется во-ображаемая точка С положение которой характеризует распределение массы всей системы. Слайд 61Радиус-вектор центра масс:
Где:
-масса и радиус вектор ¡-ой материальной
точки
-число материальных точек в системе
-масса всей системыСкорость центра масс:
Импульс системы равен произведению массы сис-темы на скорость её центра масс.
Слайд 62Закон движения центра масс
Центр масс системы двигается как материаль-ная точка,
в которой сосредоточена вся мас- са системы, и на которую
действует сила равная геометрической сумме всех внеш-них сил, действующих на систему.Центр масс замкнутой системы либо движет-ся прямолинейно и равномерно, либо оста-ётся неподвижным.
Слайд 63Движение тел переменной массы
В начальный момент времени
, масса , начальная скорость
В момент
времени : масса , скорость , скорость истечения га-зов относительно ракетыВ момент времени , масса ра-кеты , масса сгоревшего то-плива , скорость ракеты
Слайд 64Изменение импульса системы за время dt:
Если на тело действуют внешние
силы то :
где :
-реактивная силаЕсли u противоположно по направлению с v то ракета разгоняется, если совпадает то тормозится.
Слайд 65Уравнение движения тела переменной массы
(Уравнение Мещерского)
Если на
движущуюся ракету не действуют внешние силы (F=0) и скорость выбрасываемых газов постоянна то:Значение постоянной интегрирования С определим из начальных условий. Если и то
Следовательно:
Слайд 66Формула Циолковского
Формула Циолковского показывает:
Чем больше конечная масса ракеты, тем больше
должна быть стартовая масса ракеты.
Чем больше скорость истечения газов, тем
больше может быть конечная масса при данной стартовой массе ракеты. Слайд 68Энергия
Энергия – универсальная мера различных форм движения и взаимодействия.
С
различными формами движения материи связывают различные формы энергии (механическую, тепловую,
ядерную и т.д.)Во всех случаях энергия отданная (в той или иной форме одним телом другому телу, равна энергии полученной последним телом.
Слайд 69 Изменение механического движения тела вызывается силами, действующими на него со
стороны других тел. Что бы количествен-но охарактеризовать процесс обмена энер-гией
между взаимодействующими телами в механике вводится понятиеРабота силы
Слайд 70Работа силы
Если тело движется прямолинейно и на него дей-ствует
постоянная сила , которая составляет угол
с направлением перемещения, то работа этой силы будет равна произведению проекции силы на направление перемещения умноженной на перемещение точки приложения силыЕдиница измерения работы- джоуль ( Дж)
1 Дж=1Н м
Слайд 71 Элементарной работой силы на перемещении будет
называться скалярная величина
где:
-угол между векторами
и -элементарный путь
-проекция вектора на вектор
Работа силы на участке траектории от точки 1 до 2 равна сумме элементарных работ на отдельных бесконечно малых участках пути
Слайд 72 Для вычисления этого интеграла надо знать за-висимость силы от пути
вдоль траектории 1-2.
На графике работа А определяется площадью за-штрихованной фигуры.
Если
тело двигается прямолинейноа параметры F и α постоянны, то
При работа силы положительна,
и совпадает по направлению с вектором ,
при работа силы отрицательна, при
(направление перпендикулярно перемещению) работа равна нулю.
Слайд 73Мощность
Что бы охарактеризовать скорость соверше-ния работы вводят понятие мощность
единица измерения
мощности- Ватт (Вт)
1 Вт=1 Дж/с
Мощность равна скалярному произведе-нию вектора силы
на вектор скорости с ко-торой движется точка приложения силы.Слайд 75Кинетическая энергия механической системы – энергия механического движения этой системы.
(В различных источниках обозначается:
)Работа силы на пути который тело прошло за время возрастания скорости от 0 до идет на увеличение кинетической энергии
По 2 закону Ньютона и умножая на пере-мещение можно получить равенство:
Слайд 76Тело массой m двигающееся со скоростью v обладает кинетической энергией
Кинетическая
энергия зависит только от скорости и массы тела то есть
кинетическая энергия систе-мы есть функция состояния её движения.Движение рассматривается в инерциальной сис-теме отсчета. В разных инерциальных системах отсчета, двигающихся относительно друг друга скорость тела, а значит и кинетическая энергия будут неодинаковы. Значит кинетическая энергия зависит от выбора системы отсчета.
Слайд 77Стационарные силовые поля называются потен-циальными а силы действующие в них
консерва-тивными , если работа этих сил на любом замк-нутом контуре
равна нулю (0). Если же работа со-вершаемая силой зависит от траектории переме-щения тела то такая сила называется диссипатив-ной.Работа сил потенциального поля при переносе тела из одного положения в другое не зависит от вида пути по которому идет перемещение, а оп-ределяется только положением начальной и ко-нечной точек.
Слайд 78Потенциальная энергия механической системы-механическая энергия системы тел, определяемая их взаимным
расположением и характером сил взаимодействия между ними. (В различных источниках
обозначается: ).Выберем в консервативной системе
точку P(x,y,z) с заданными координа-
тами и найдём работу А которую со-
вершают силы поля при переходе частицы из на-чала координат в эту точку. Тогда величина этой работы с обратным знаком будет называться: потенциальной энергией частицы в точке P(x,y,z)
Слайд 79Работа консервативных сил при элементарном из-менении конфигурации системы, равна обратному
значению приращения потенциальной энергии.
где: С- постоянная интегрирования.
Потенциальная энергия может иметь
отрицатель-ное значение (кинетическая энергия всегда имеет положительное значение).Конкретный вид функции зависит от характера силового поля.
Потенциальная энергия является функцией состояния системы, зависит только от конфигура-ции системы и её положения по отношению к внешним телам.
Слайд 80Виды потенциальной энергии
Потенциальная энергия тела массой m поднятого на высоту
h над поверхностью Земли
Эта формула выводится непосредственно из того, что
потенциальная энергия равна работе силы тя-жести при падении тела с высоты h на поверхность Земли. Соответственно если h=0 то .Если принять за 0 значение потенциальной энер-гии тела на поверхности Земли , то потенциальная энергия тела лежащего на дне шахты глубиной h будет равна
Слайд 81Потенциальная энергия упругодеформированного тела (пружины):
Сила упругости пропорциональна деформации
где:
-проекция силы упругости на ось х (знак
– показывает что сила направлена в сторону противоположную деформации.-коэффициент упругости (жесткость)
-деформирующая сила
Слайд 82Полная механическая энергия системы
Полная механическая энергия системы Е-энергия механического движения
и взаимо-действия, равна сумме кинетической и по-тенциальных энергий.
Слайд 83Закон сохранения энергии
Закон сохранения энергии- результат обоб-щения многих экспериментальных данных.
Идея
закона принадлежит М. В. Ломоносо-ву (1711-1765) изложившему закон сохра-нения материи
и движения, количествен-ные характеристики выведены Ю. Майером (1814-1878) и Г. Гельмгольцем (1821-1894).Слайд 84 Пусть имеется система состоящая из n материаль-ных точек где соответственно:
-массы точек.
-скорости точек.
-равнодействующие внутренних кон-сервативных сил действующих на каждую точку.
- равнодействующие внешних консер-вативных сил действующих на каждую точку.
- равнодействующие внешних некон-сервативных сил действующих на каждую точку.
Используя 2 закон Ньютона можно составить систе-му уравнений:
Слайд 85
Так как двигаясь под действием сил, точки за ин-тервал времени
совершат перемещения равные .
, то ,учитывая что можно преобразовать систему:Слайд 86Сложим уравнения системы и получим:
Первый член левой части равенства будет
равен:
где -приращение кинетической энергии системы
Второй член уравнения
равен эле-ментарной работе внутренних и внешних консер-вативных сил (со знаком -) т.е. равен элементар-ному приращению потенциальной энергииСлайд 87 Правая часть равенства задаёт работу внешних неконсервативных сил действующих на
систему.
При переходе системы из состояния 1 в состояние 2
Изменение полной
механической энергии систе-мы при переходе системы из одного состояния в другое равно работе совершенной при этом внешними неконсервативными силами.Слайд 88Закон сохранения механической энергии
В системе тел между которыми действуют только
консервативные силы полная механическая энергия сохраняется то есть не изменяется
со временем.Слайд 89Механические системы в которых действуют толь-ко консервативные силы (внешние и
внутренние) называются консервативными системами.
Системы в которых механическая энергия посте-пенно уменьшается
за счёт преобразования в дру-гие (немеханические) формы энергии называются диссипативными. Процесс носит название диссипации или рассеяния энергии.Все системы-диссипативные. В системе где дейст-вуют неконсервативные силы (силы трения), ме-ханическая энергия не сохраняется. Однако, при исчезновении механической энергии всегда воз-никает эквивалентное количество энергии другого типа (внутренней, химической и т.д.)
Слайд 90Энергия никогда не исчезает и не появляется вновь, она превращается
из одного вида в другой.
Данное выражение- физическая сущность фундаментального закона
природы: ЗАКОНА СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ