Физика ч. II

тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна

электрическая проводимость проводника

[См]

R [Ом]

Для однородного линейного проводника сопротивление R прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения S:

 - коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением.

Закон Ома

вещества проводника
,
или
закон Ома в дифференциальной форме:
Из опыта известно, что:


Проводимость

тока в этом случае:
Мощность тока:
Если ток проходит по неподвижному металлическому

закон Джоуля – Ленца:

Закон Джоуля-Ленца

обобщенное выражение закона Джоуля - Ленца в дифференциальной форме:
Удельная тепловая

обозначим через 12, а приложенную на концах участка разность потенциалов

Работа A12 всех сил (сторонних и электростатических), совершаемая над носителями тока:

Если э.д.с. способствует движению положительных зарядов в выбранном направлении (в направлении 1-2), то 12 > 0.

За время t в проводнике выделяется теплота:

Закон Ома для неоднородного участка цепи в интегральной форме

Если электрическая цепь замкнута, то 1 = 2:

или

закон Ома для замкнутой цепи

Закон Ома

Эта задача решается более просто с помощью двух правил Кирхгофа.
Любая

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления, соответствующих участков этого контура равна алгебраической сумме э.д.с., встречающихся в этом контуре:

Правила Кирхгофа

е. электроны, слабо связанные с ионами кристаллической решетки металла (опыт

При образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий, согласно электронной теории металлов, свойствами идеального газа.

Противоречия: температурная зависимость сопротивления, средняя длина свободного пробега электронов, теплоемкость металлов

Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла - Больцмана, а квантовой статистикой.

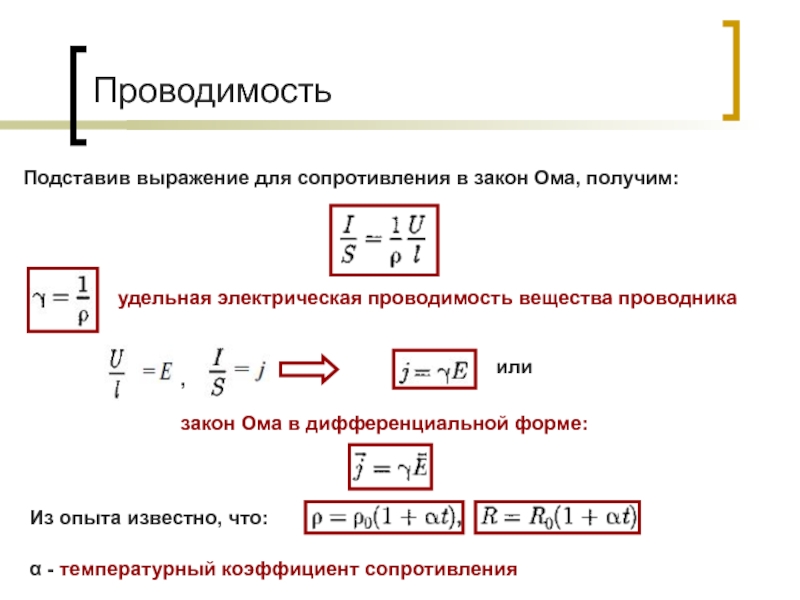
Проводимость металла

которую нужно затратить для удаления электрона из металла в вакуум,

1. Если электрон по какой-то причине удаляется из металла, то в том месте, которое электрон покинул, возникает избыточный положительный заряд и электрон притягивается к индуцированному им самим положительному заряду

Причины:

2. Отдельные электроны, покидая металл, удаляются от него на расстояния порядка атомных и создают тем самым над поверхностью металла «электронное облако», плотность которого быстро убывает с расстоянием. Это облако вместе с наружным слоем положительных ионов решетки образует двойной электрический слой, поле которого подобно полю плоского конденсатора.

 - поверхностный скачок потенциала

Работа выхода