Слайд 1Лопастные насосы и их классификация
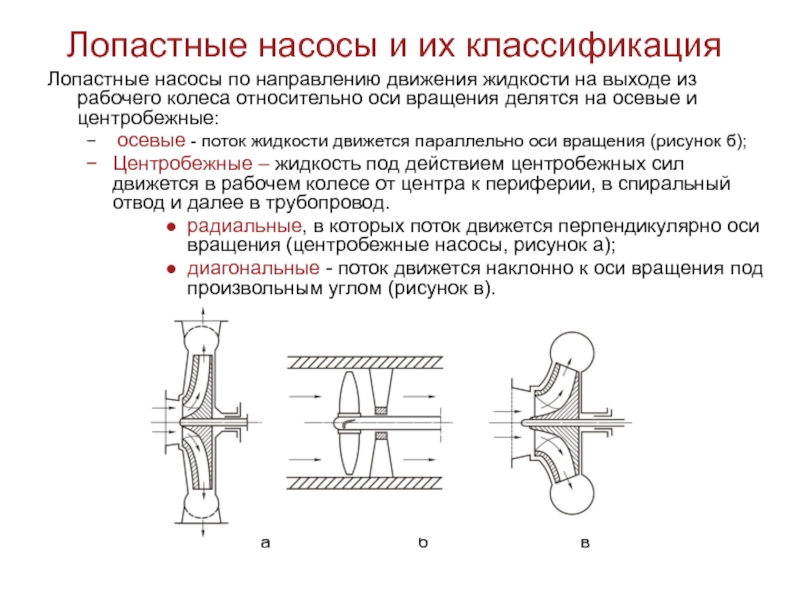
Лопастные насосы по направлению движения
жидкости на выходе из рабочего колеса относительно оси вращения делятся
на осевые и центробежные:
осевые - поток жидкости движется параллельно оси вращения (рисунок б);
Центробежные – жидкость под действием центробежных сил движется в рабочем колесе от центра к периферии, в спиральный отвод и далее в трубопровод.
радиальные, в которых поток движется перпендикулярно оси вращения (центробежные насосы, рисунок а);
диагональные - поток движется наклонно к оси вращения под произвольным углом (рисунок в).
а б в
Слайд 2Лопастные насосы и их классификация
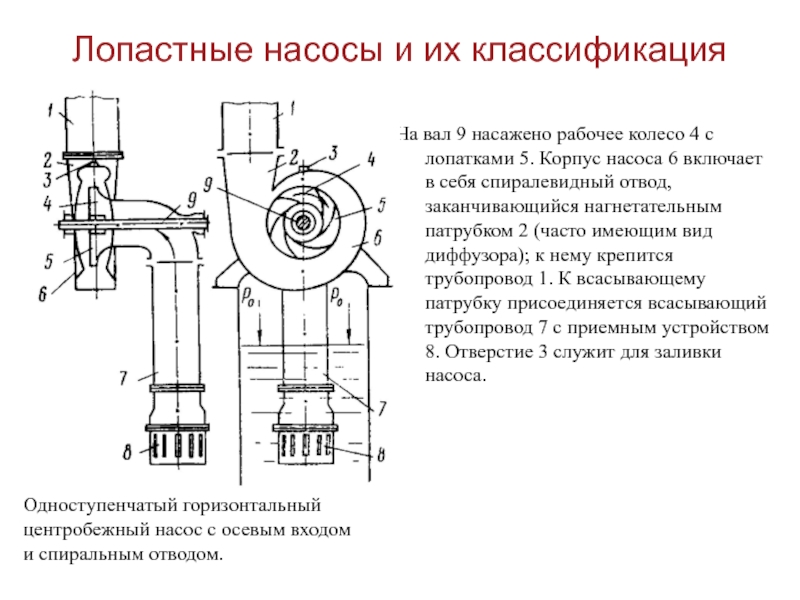
На вал 9 насажено рабочее колесо
4 с лопатками 5. Корпус насоса 6 включает в себя
спиралевидный отвод, заканчивающийся нагнетательным патрубком 2 (часто имеющим вид диффузора); к нему крепится трубопровод 1. К всасывающему патрубку присоединяется всасывающий трубопровод 7 с приемным устройством 8. Отверстие 3 служит для заливки насоса.
Одноступенчатый горизонтальный
центробежный насос с осевым входом
и спиральным отводом.
Слайд 3Лопастные насосы и их классификация
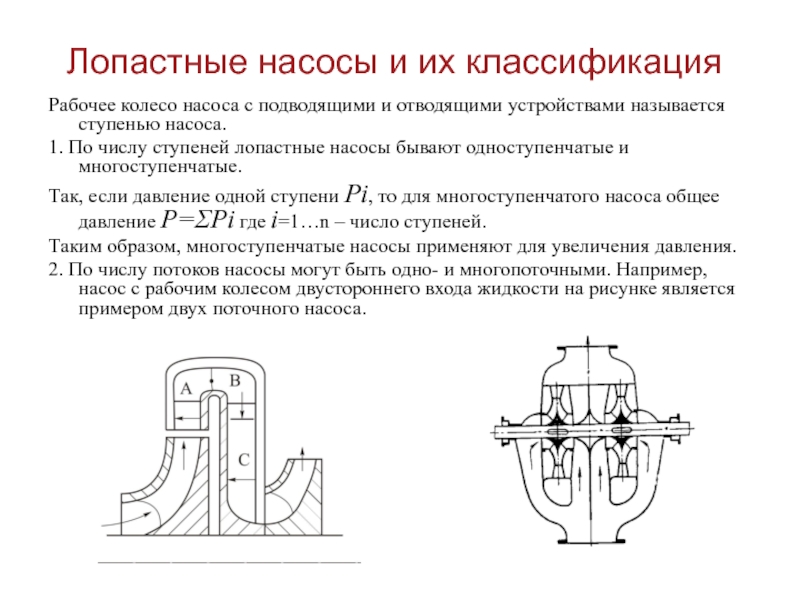
Рабочее колесо насоса с подводящими и
отводящими устройствами называется ступенью насоса.
1. По числу ступеней лопастные насосы
бывают одноступенчатые и многоступенчатые.
Так, если давление одной ступени Pi, то для многоступенчатого насоса общее давление P=ΣPi где i=1…n – число ступеней.
Таким образом, многоступенчатые насосы применяют для увеличения давления.
2. По числу потоков насосы могут быть одно- и многопоточными. Например, насос с рабочим колесом двустороннего входа жидкости на рисунке является примером двух поточного насоса.
Слайд 4Лопастные насосы и их классификация
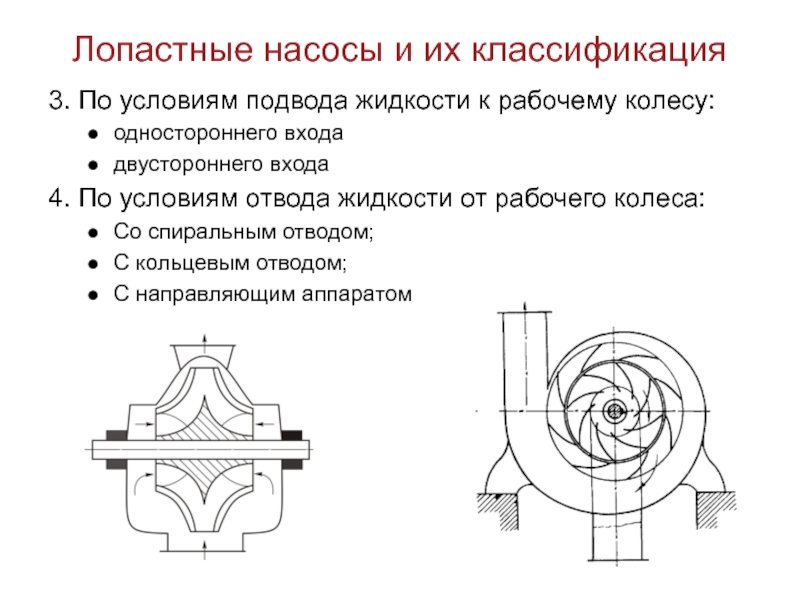
3. По условиям подвода жидкости к
рабочему колесу:
одностороннего входа
двустороннего входа
4. По условиям отвода жидкости от
рабочего колеса:
Со спиральным отводом;
С кольцевым отводом;
С направляющим аппаратом
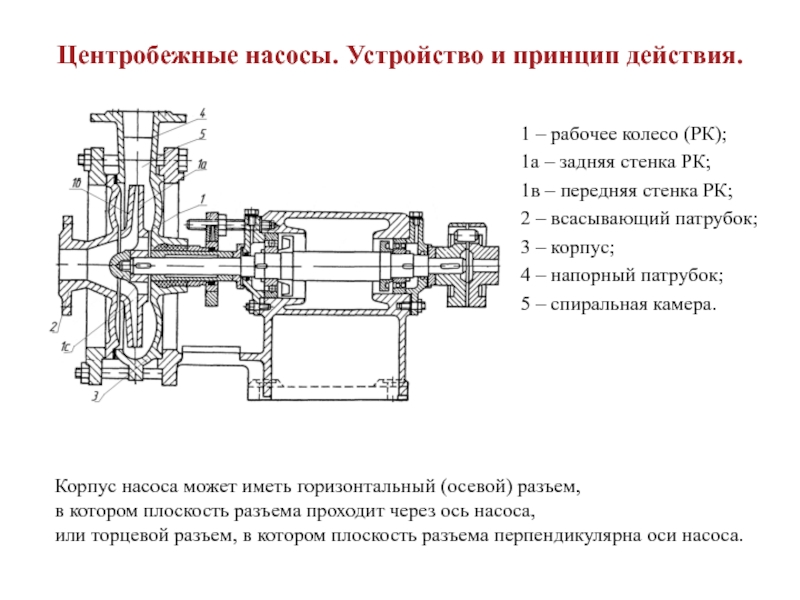
Слайд 5Центробежные насосы. Устройство и принцип действия.
1 – рабочее колесо (РК);
1a
– задняя стенка РК;
1в – передняя стенка РК;
2 – всасывающий
патрубок;
3 – корпус;
4 – напорный патрубок;
5 – спиральная камера.
Корпус насоса может иметь горизонтальный (осевой) разъем,
в котором плоскость разъема проходит через ось насоса,
или торцевой разъем, в котором плоскость разъема перпендикулярна оси насоса.
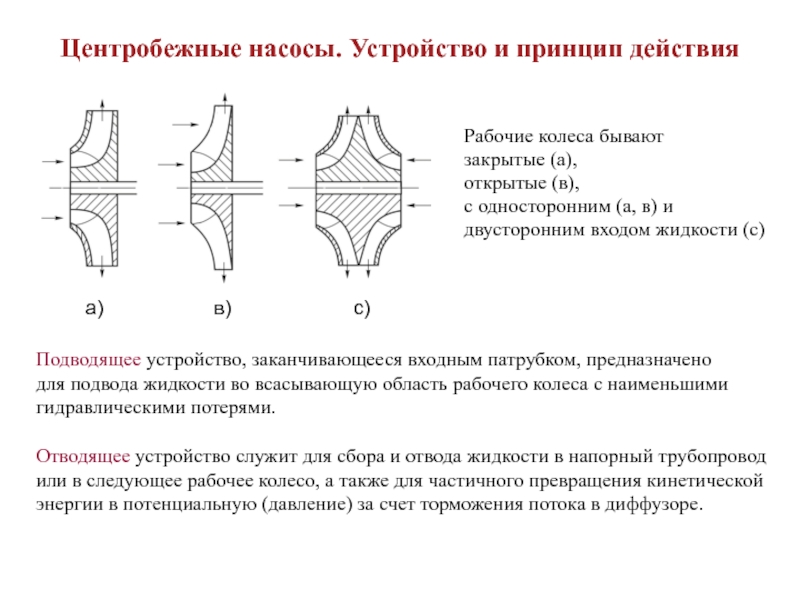
Слайд 6Центробежные насосы. Устройство и принцип действия
Рабочие колеса бывают
закрытые (а),
открытые (в),
с односторонним (а, в) и
двусторонним входом жидкости
(с)
а) в) с)
Подводящее устройство, заканчивающееся входным патрубком, предназначено
для подвода жидкости во всасывающую область рабочего колеса с наименьшими
гидравлическими потерями.
Отводящее устройство служит для сбора и отвода жидкости в напорный трубопровод
или в следующее рабочее колесо, а также для частичного превращения кинетической
энергии в потенциальную (давление) за счет торможения потока в диффузоре.
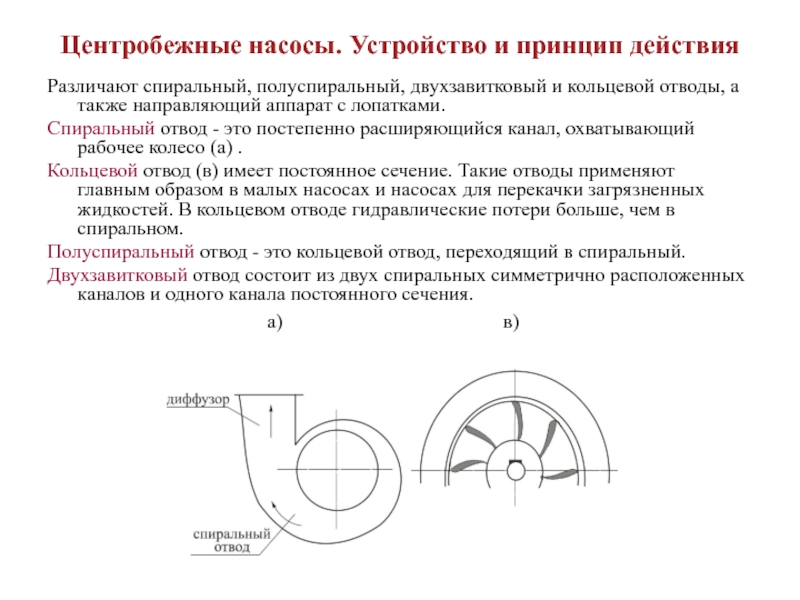
Слайд 7Центробежные насосы. Устройство и принцип действия
Различают спиральный, полуспиральный, двухзавитковый и
кольцевой отводы, а также направляющий аппарат с лопатками.
Спиральный отвод -
это постепенно расширяющийся канал, охватывающий рабочее колесо (а) .
Кольцевой отвод (в) имеет постоянное сечение. Такие отводы применяют главным образом в малых насосах и насосах для перекачки загрязненных жидкостей. В кольцевом отводе гидравлические потери больше, чем в спиральном.
Полуспиральный отвод - это кольцевой отвод, переходящий в спиральный.
Двухзавитковый отвод состоит из двух спиральных симметрично расположенных каналов и одного канала постоянного сечения.
а) в)
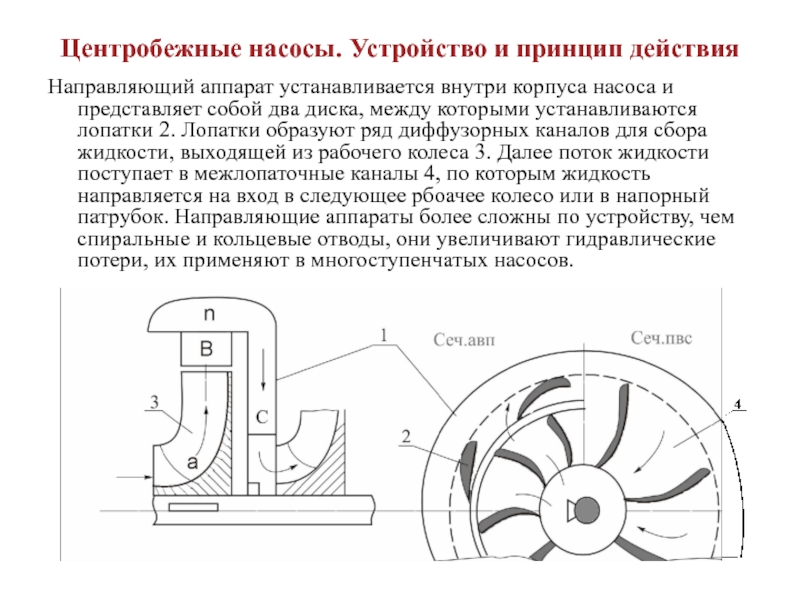
Слайд 8Центробежные насосы. Устройство и принцип действия
Направляющий аппарат устанавливается внутри корпуса
насоса и представляет собой два диска, между которыми устанавливаются лопатки
2. Лопатки образуют ряд диффузорных каналов для сбора жидкости, выходящей из рабочего колеса 3. Далее поток жидкости поступает в межлопаточные каналы 4, по которым жидкость направляется на вход в следующее рбоачее колесо или в напорный патрубок. Направляющие аппараты более сложны по устройству, чем спиральные и кольцевые отводы, они увеличивают гидравлические потери, их применяют в многоступенчатых насосов.
Слайд 9Осевое усилие в центробежных насосах.
Способы уравновешивания
Рабочее колесо одностороннего
входа представляет собой неуравновешенную систему из-за отсутствия симметрии относительно плоскости,
перпендикулярной оси вращения насоса. В результате возникает осевая сила давления Р, направленная в сторону входного отверстия рабочего колеса.
Для ориентировочных расчетов можно воспользоваться формулой
P0=π/4·(D12-d2 )·ρgН
где D1=2Rв и d - диаметры входного отверстия колеса и вала; Н – напор насоса
Слайд 10Осевое усилие в центробежных насосах.
Способы уравновешивания
Для уравновешивания осевых сил
применяются следующие способы:
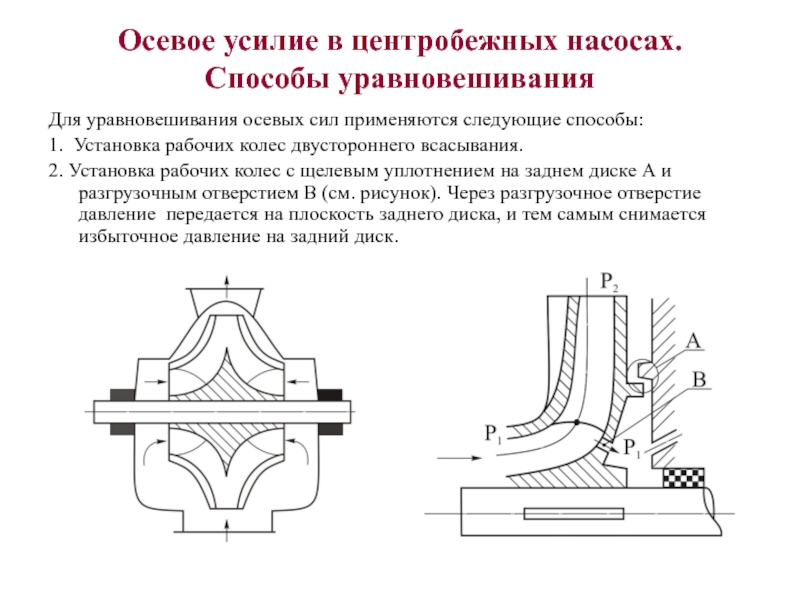
1. Установка рабочих колес двустороннего всасывания.
2. Установка рабочих
колес с щелевым уплотнением на заднем диске А и разгрузочным отверстием В (см. рисунок). Через разгрузочное отверстие давление передается на плоскость заднего диска, и тем самым снимается избыточное давление на задний диск.
Слайд 11Осевое усилие в центробежных насосах.
Способы уравновешивания
3. Установка саморегулирующего устройства
(рисунок) (гидравлической пяты). За последней ступенью многоступенчатого насоса на валу
устанавливается диск I. Жидкость после рабочего колеса перетекает из камеры А в камеру В через щелевое уплотнение С, где давление Р2 падает до давления , и отводится во всасывающую полость насоса.
Так как давление в камере А выше, чем в камере Б, на диск действует
усилие, разгружающее осевую силу, стремящуюся сместить колесо
в сторону всасывания, т.е. разгружающая сила зависит от перепада
давлений, возрастающего в случае уменьшения зазора под действием
осевой силы и наоборот.
Слайд 12Осевое усилие в центробежных насосах.
Способы уравновешивания
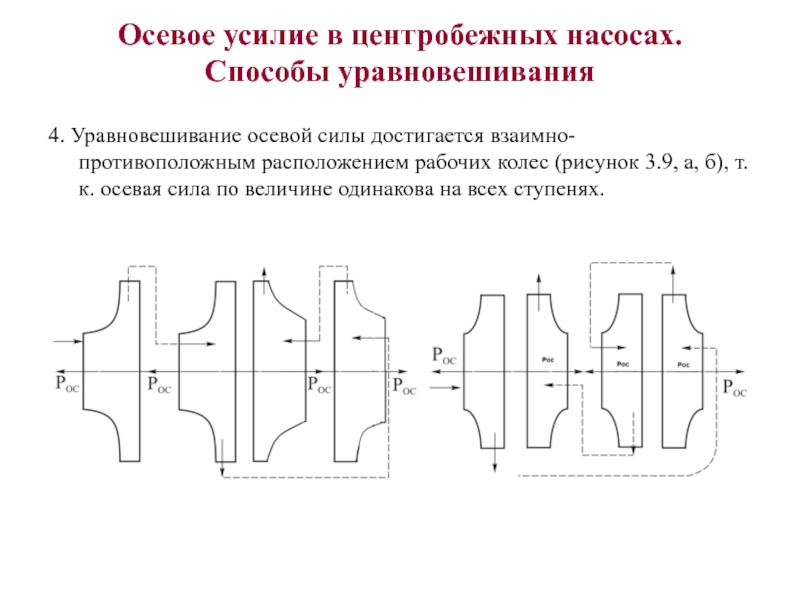
4. Уравновешивание осевой силы
достигается взаимно-противоположным расположением рабочих колес (рисунок 3.9, а, б), т.к.
осевая сила по величине одинакова на всех ступенях.
Слайд 13Движение жидкости в каналах рабочего колеса ЦН
Теоретические уравнения движения жидкости
в межлопаточных каналах динамических гидромашин (лопаточных насосов и гидротурбин) получены
Л.Эйлером при следующих двух допущениях:
1. Жидкость идеальная, т.е. гидравлические сопротивления не учитываются.
2. Жидкость движется в виде бесконечного числа элементарных струек, строго повторяющих форму лопаток.
Эти допущения облегчают теоретическое исследование движения жидкости в лопаточных системах, но в дальнейшем требуют внесения существенных поправок на основании экспериментальных исследований.
Движение каждой частицы жидкости потока в рабочем колесе является сложным, абсолютная скорость, которой складывается из переносной и относительной скоростей.
Скорость переносного U движения - это линейная скорость вращательного движения точки рабочего колеса, где в данный момент находится частица жидкости. Эта скорость направлена по касательной к окружности, на которой находится частица.
Относительная скорость w – это скорость перемещения частицы относительно лопатки колеса: вектор относительной скорости направлен по касательной к лопатке.
Абсолютная скорость c определяется как векторная сумма:

Слайд 14Движение жидкости в каналах рабочего колеса ЦН
Окружные линейные скорости
будут
равны: U1=ω·R1; U2=ω·R2, где
ω – скорость вращения колеса;
R1 – радиус
входной точки струйки
R2 – наружный радиус рабочего колеса
β1,β2 - это углы между направлением относительной скорости w и в обратном направлении окружной скорости (-U). Углы, определяющие форму лопатки рабочего колеса.
Углы между направлением
абсолютной скорости С и
окружной скорости U обозначаются
α1 и α2
Слайд 15Движение жидкости в каналах рабочего колеса ЦН
Из уравнения неразрывности потока
жидкости, протекающего через рабочее колесо, следует:
F1·C1r= F2·C2r=Qт=const,
где F1, F2
– площади поперечного сечения в каналах колеса на входе и выходе с образующей, нормальной к радиальной скорости;
C1r, C1r - радиальные составляющие абсолютных скоростей на входе и выходе;
F1=(πD1-δ1z)·b1; F2=(πD2-δ2z)·b2
где D1 и D2 – соответственно диаметры на входе в межлопаточные каналы и выходе из них;
δ1 и δ2 – ширина лопатки (канала);
b1 и b2 – толщина лопаток, z - число лопаток.
QT=F·Cr – представляет собой идеальную подачу рабочего колеса центробежного насоса.
Слайд 16Основное уравнение турбомашин Эйлера
Уравнение моментов количества движения: Мкр=Qm·(C1uR1-C2uR2), где
Qm – массовый расход,
R1, R2 – внутренний и наружный
радиусы колеса,
С1u, C2u – проекция вектора абсолютной скорости потока на вектор переносной скорости U
С1u=C1·cosα1, C2u=C2·cosα2
Nг=QρgHT=QmgHT и Nг=Мкр·ω
т.о. НТ= (C1R1·cosα1 -C2R2·cosα2)·ω/g,
Если вход жидкости в рабочее колесо насоса радиальный (=90°),то
НТ= C2R2·cosα2·ω/g= C2·cosα2·U2/g
Слайд 17Теоретический напор. Уравнение Бернулли.
Теоретический напор, приобретаемый жидкостью в каналах рабочего
колеса НТ=Н2-Н1;
где Н2 и Н1- удельная энергия потока на
выходе и входе в рабочее колесо; Согласно уравнению Бернулли:
Н2=z2+P2/ρg+C22/2g; Н1=z1+P1/ρg+C12/2g →
→ НТ= (z2-z1) +(P2/ρg-P1/ρg)+ (C22/2g-C12/2g)
(z2-z1) - изменение удельной энергии положения
(P2/ρg-P1/ρg) - приращение удельной потенциальной энергии (энергии давления) представляет статический напор колеса НСТ;
(C22/2g-C12/2g) - приращение удельной кинетической энергии в абсолютном движении составляет динамический напор колеса НДИН;
Таким образом, НТ=НСТ+НДИН
Слайд 18Выбор угла установки лопатки на выходе
т.к НТ= C2·cosα2·U2/g (по ф.
Эйлера для α1=90º, а C2·cosα2=U2- С2r·ctgβ2
С2r=QT/F2 , то
НТ=U2 /g·(U2-
QTctgβ2/F2)
При β<90°, НТ≤ U22 /g, НT убывает линейно по мере увеличения QT; лопатки рабочего колеса отогнуты назад по ходу вращения;
при β = 90°, НТ=U22 /g=const, НT не зависит от QT, а лопатки радиальные;
при β >90°, НТ>U22 /g, НT возрастает линейно по мере увеличения QT, лопатки загнуты вперед по ходу вращения;
Слайд 19Выбор угла установки лопатки на выходе
угол β2
, при этом C2=С1=С2r; α2= 90°.
→ НТ= C2·cosα2·U2/g=0,
НДИН=C22/2g-C12/2g=0,
т.к. С1=С2;
Следовательно, и НСТ=0.
2. угол β2=90°, ω2=С1=С2r; НТ=U22 /g;
НДИН=C22/2g-C12/2g= U22 /2g;
→ НСТ= U22 /2g.
3. угол β2>90°, НТ= C2·cosα2·U2/g= =2U2·U2/g= 2U22/g;
НДИН=C22/2g-C12/2g= (2U2)2 /2g= 2U22 /g;
→ НСТ= 0.
Слайд 20Выбор угла установки лопатки на выходе
С увеличением β2 возрастает
напор НТ, при этом при углах β2 >90 доля НДИН
растет интенсивно, а доля НСТ падает и при β2=β2max становится равной нулю;
Наибольшая величина НСТ имеет место при угле β2=90 и равна половине всего напора;
Угол β2 не может быть меньше β2min (α2= 90°), так как при β2<β2min величина напора НТ приобретает отрицательное значение C2·cosα2<0, C2 направлена в сторону, обратную
вращению колеса, насос переходит в режим работы турбины;
Предельное значение угла β2max находится из условия C2·cosα2=2U2.
Исходя из требований получения максимальной НСТ целесообразно выбрать углы β2min<β2<90º. В этом случае имеет большую долю статического напора и потери энергии на преобразование кинетической энергии потока в энергию давления в отводящих устройствах будут минимальными.
Установлено, что оптимальным является β2=15º÷45º.
Слайд 21Влияние конечного числа лопаток на величину теоретического напора
В канале
A − струйное течение по схеме Эйлера. Элементарные струйки повторяют
очертания лопаток и скорости во всех этих элементарных струйках на одинаковых радиусах равны.
В канале В − циркуляционное движение при нулевой подаче (выход из межлопаточного канала закрыт). Жидкость в объеме этого канала получает вращательное движение относительно стенок межлопаточного канала в направлении обратном направлению вращения рабочего колеса.
В канале С − поле скоростей (эпюра скоростей) в живом сечении межлопаточного канала, полученное в результате сложения скоростей поступательного движения по схеме Эйлера и циркуляционного, вызванного вращением рабочего колеса. Из эпюры скоростей видно, что струйки, идущие около передней поверхности лопатки, имеют меньшие скорости, а струйки, идущие вблизи обратной поверхности лопаток, имеют наибольшие скорости.
Слайд 22Влияние конечного числа лопаток на величину теоретического напора
Теоретический напор НТ
для рабочего колеса с конечным числом лопаток меньше теоретического напора
при бесконечном числе лопаток НТ∞. Эта потеря напора учитывается специальной поправкой кП (по формулам Г.Ф. Проскура и К. Пфлейдерера).
НТ= НТ∞/(1- кП);
z – число лопаток;
Ψ – коэффициент, зависящий от шероховатости проточной части колеса.
Ψ= 0,8…1,0 для насосов с лопаточным направляющим аппаратом;
Ψ =1,0…1,3 для насосов со спиральным отводом.
Приблизительно кП= НТ/ НТ∞=0,7…0,9
Слайд 23Гидравлические, механические и объемные потери в центробежном насосе. Мощность и
КПД насоса.
Потребляемая мощность расходуется:
N= NП+ ΔNГ+ ΔNМЕХ+NУ,
где
полезная мощность NП=ρgНQ
Q – действительная подача насоса, м3/с;
Н – действительный напор насоса, м.
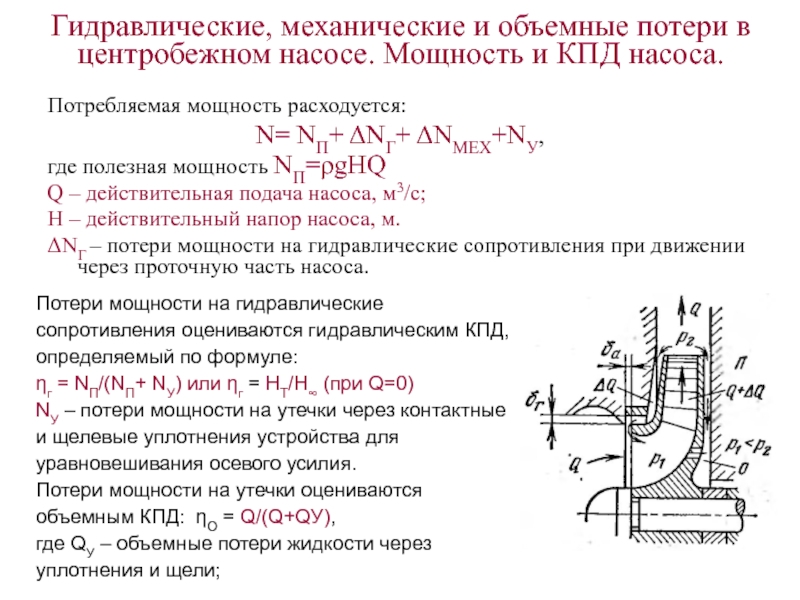
ΔNГ – потери мощности на гидравлические сопротивления при движении через проточную часть насоса.
Потери мощности на гидравлические сопротивления оцениваются гидравлическим КПД, определяемый по формуле:
ηг = NП/(NП+ NУ) или ηг = НТ/Н∞ (при Q=0)
NУ – потери мощности на утечки через контактные
и щелевые уплотнения устройства для
уравновешивания осевого усилия.
Потери мощности на утечки оцениваются
объемным КПД: ηО = Q/(Q+QУ),
где QУ – объемные потери жидкости через
уплотнения и щели;
Слайд 24Гидравлические, механические и объемные потери в центробежном насосе. Мощность и
КПД насоса.
ΔNМЕХ – потери мощности на механическое трение в подшипниках,
уплотнительных устройствах и дисковые потери, они оцениваются механическим КПД:
ηМЕХ = (N- ΔNМЕХ)/N,
Полный КПД насоса представляет собой отношение полезной мощности к мощности на валу насоса и учитывает все виды потерь:
η= NП/N = ηг ηОηМЕХ
Полный КПД дает оценку всем потерям мощности.
Для современных насосов η=0,7÷0,9.