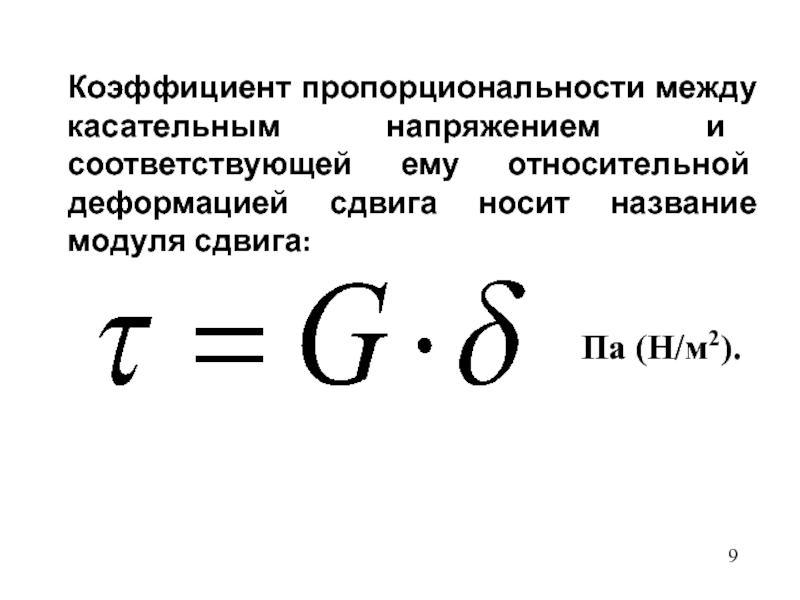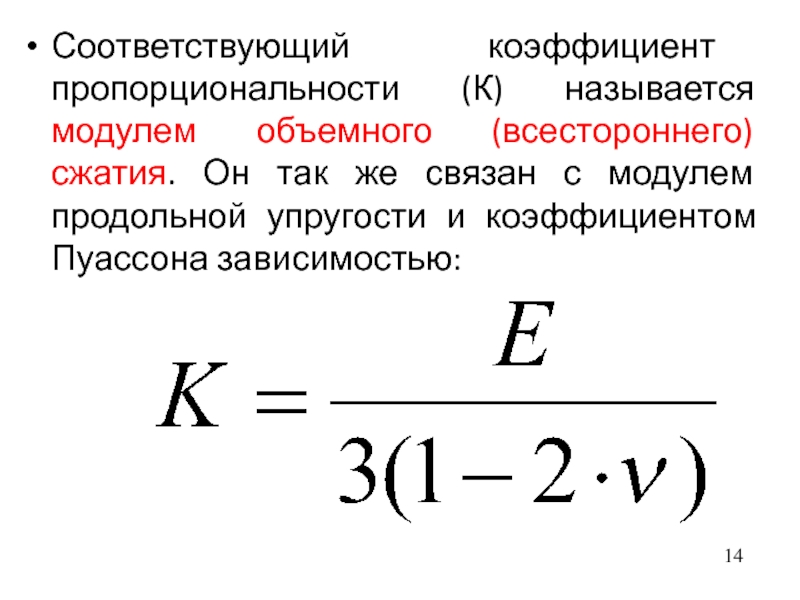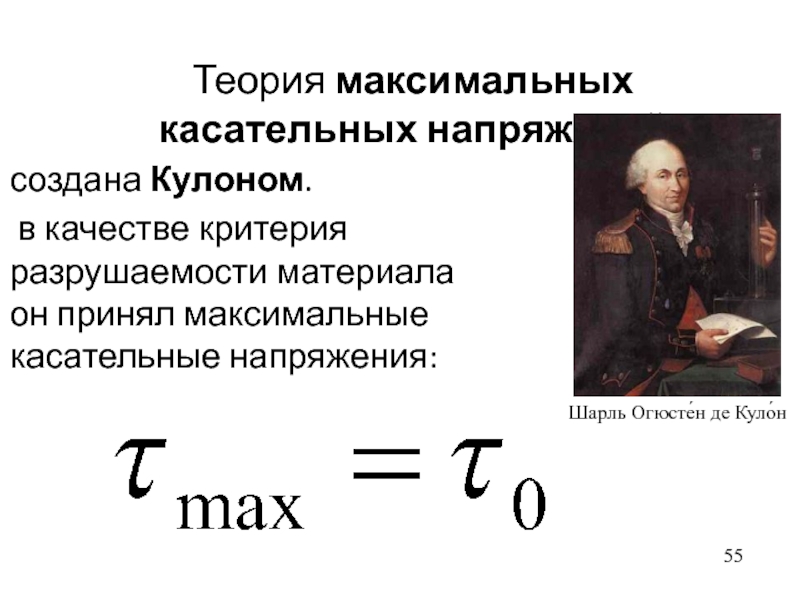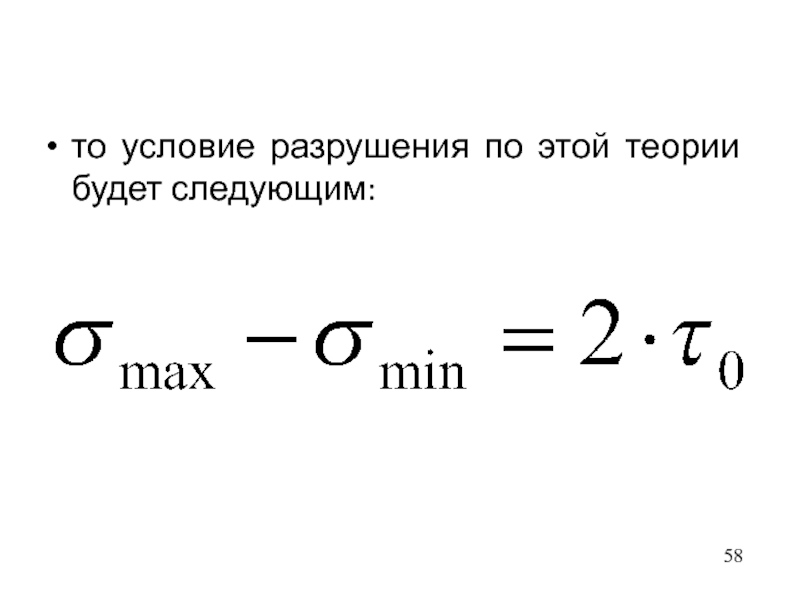Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика горных пород
Содержание
- 1. Физика горных пород
- 2. Области деформации пород
- 3. Выделяются две группы неразрушающих деформаций:пластические деформации.упругие деформации;
- 4. Причины деформацииПри изменении расстояния между атомами изменяются
- 5. В случае упругих деформаций наблюдается прямая зависимость
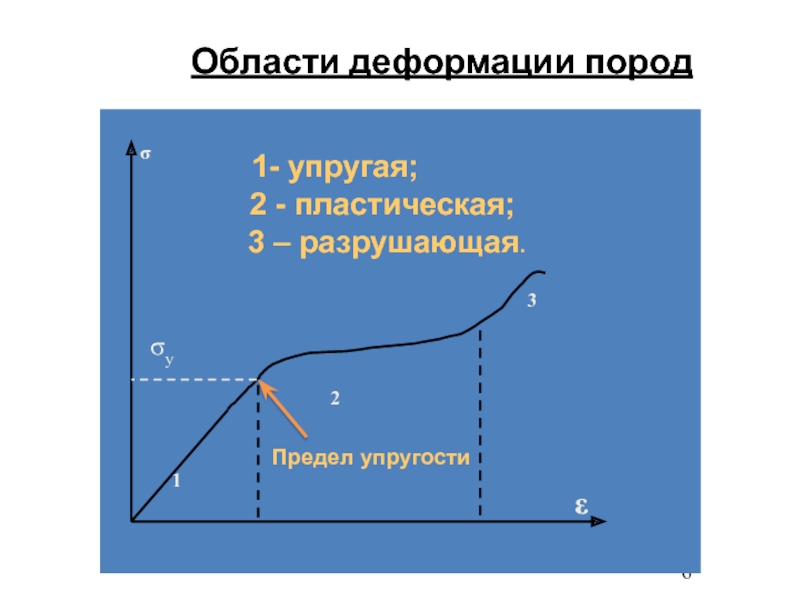
- 6. Области деформации пород 1- упругая;
- 7. Коэффициент пропорциональности между действующим продольным напряжением (растягивающим
- 8. Слайд 8
- 9. Коэффициент пропорциональности между касательным напряжением и соответствующей ему относительной деформацией сдвига носит название модуля сдвига:Па (Н/м2).
- 10. δ
- 11. На практике часто пользуются еще одним показателем
- 12. В случае идеально упругих тел достаточно знать
- 13. В условиях равномерного упругого трехосного сжатия породы
- 14. Соответствующий коэффициент пропорциональности (К) называется модулем объемного
- 15. Обобщенная зависимость изменения модуля Юнга пород от пористости может быть выражена формулой:
- 16. Пластичность - свойство горной породы в результате силового воздействия давать остаточные деформации без разрушения.
- 17. Слайд 17
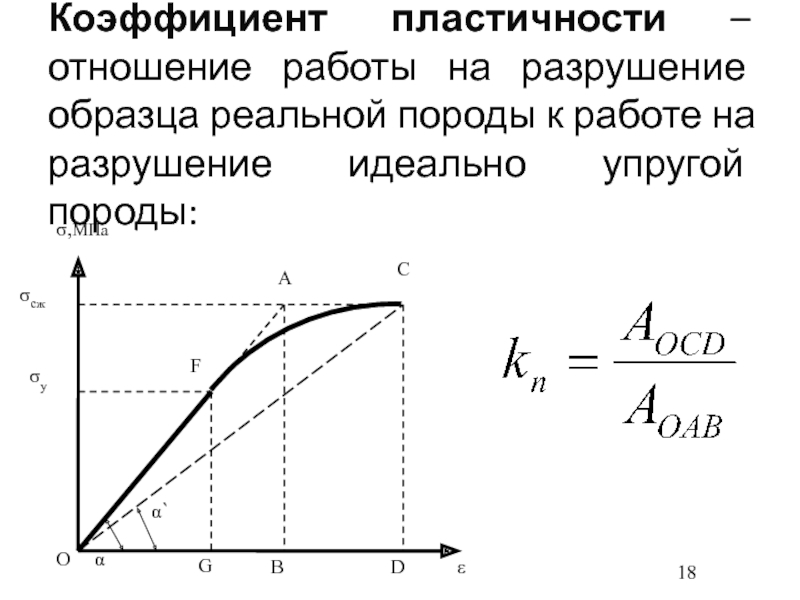
- 18. Коэффициент пластичности – отношение работы на разрушение
- 19. Глинистые породы могут быть хрупкими, пластичными и
- 20. В первом случае, это значение влажности в
- 21. Wт – Wп = ФРазность верхнего и
- 22. Реология - наука о течении вещества
- 23. Реология устанавливает общие законы образования и развития деформаций во времени.К основным реологическим параметрам относятся:ПолзучестьРелаксация напряженийДлительная прочность
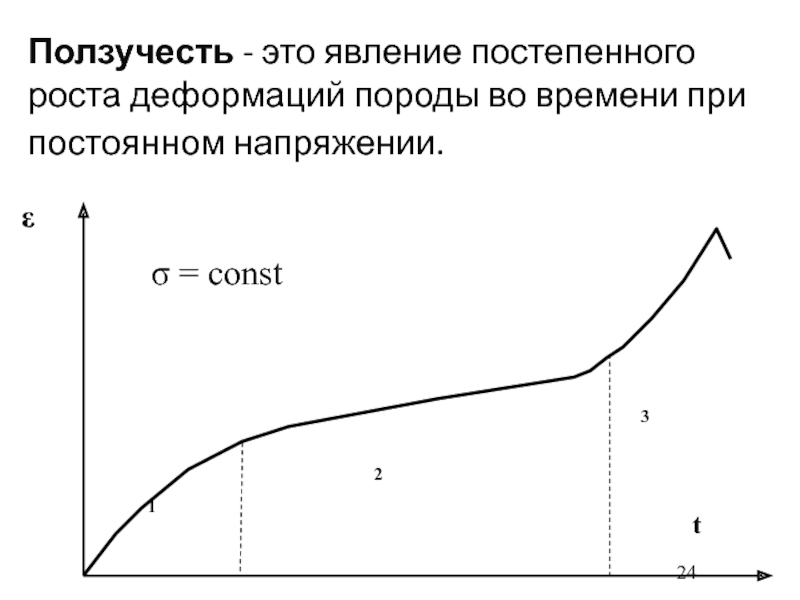
- 24. Ползучесть - это явление постепенного роста деформаций породы во времени при постоянном напряжении.
- 25. Релаксацией напряжений - называется постепенное снижение напряжений в породе во времени при постоянной деформации.
- 26. Релаксация напряжений
- 27. Время, в течение которого напряжение убывает в
- 28. Для характеристики релаксационной стойкости горной породы вводят
- 29. Опыт показывает, что при воздействии длительных напряжений
- 30. Длительная прочность пород с увеличением времени действия
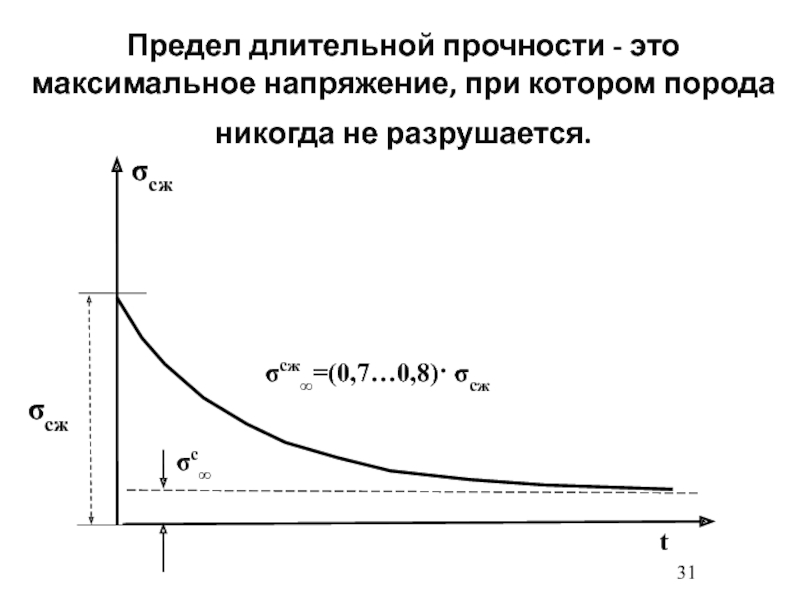
- 31. Предел длительной прочности - это максимальное напряжение, при котором порода никогда не разрушается.
- 32. Все реологические уравнения состояния пород моделируют с
- 33. твердое тело Гука (σ=Е·ε) - идеально упругое тело (пружина).
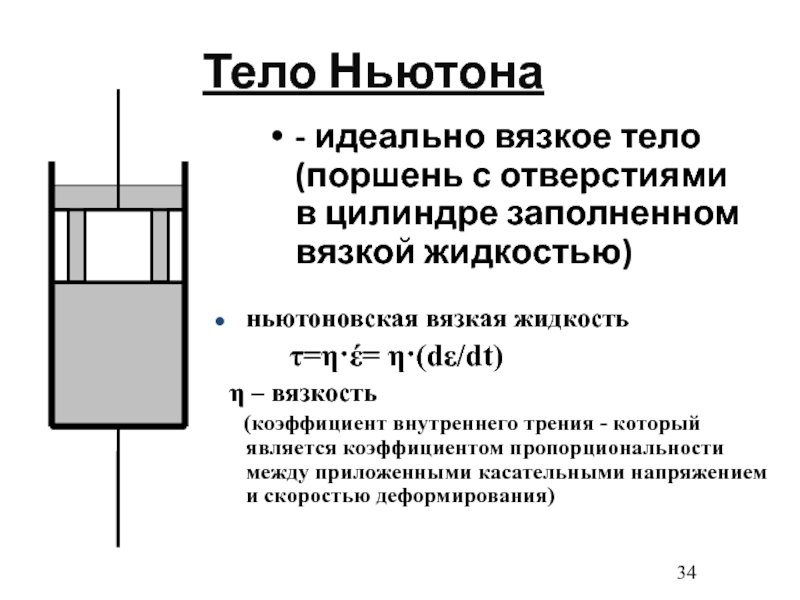
- 34. Тело Ньютона- идеально вязкое тело (поршень с
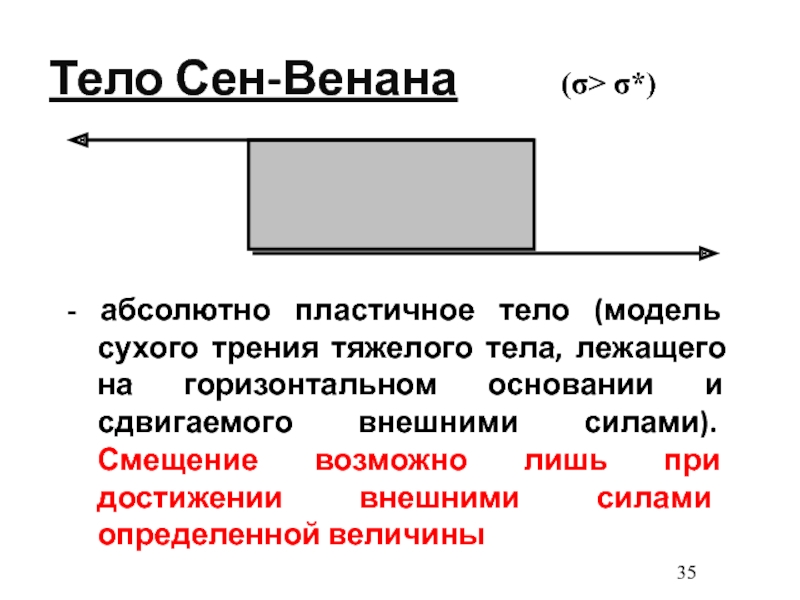
- 35. Тело Сен-Венана- абсолютно пластичное тело (модель сухого
- 36. Путем соответствующих комбинаций этих простых тел могут
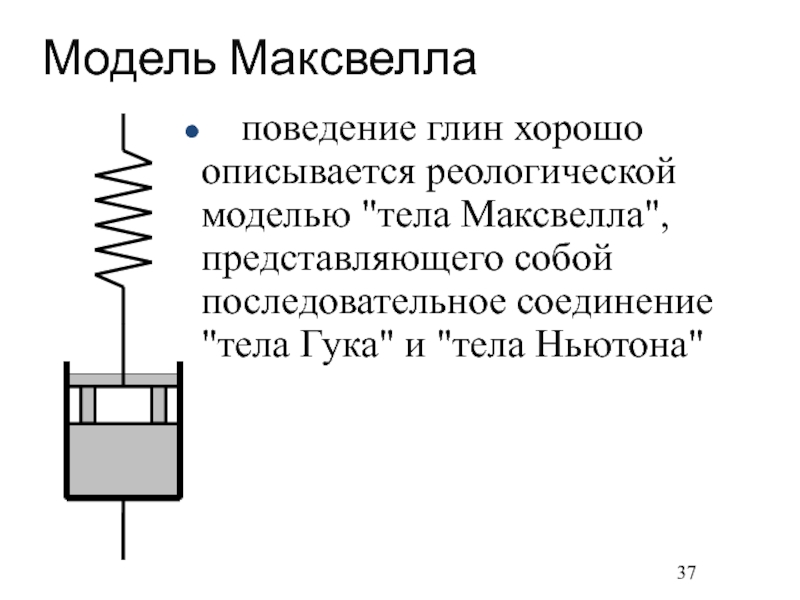
- 37. Модель Максвелла поведение глин хорошо
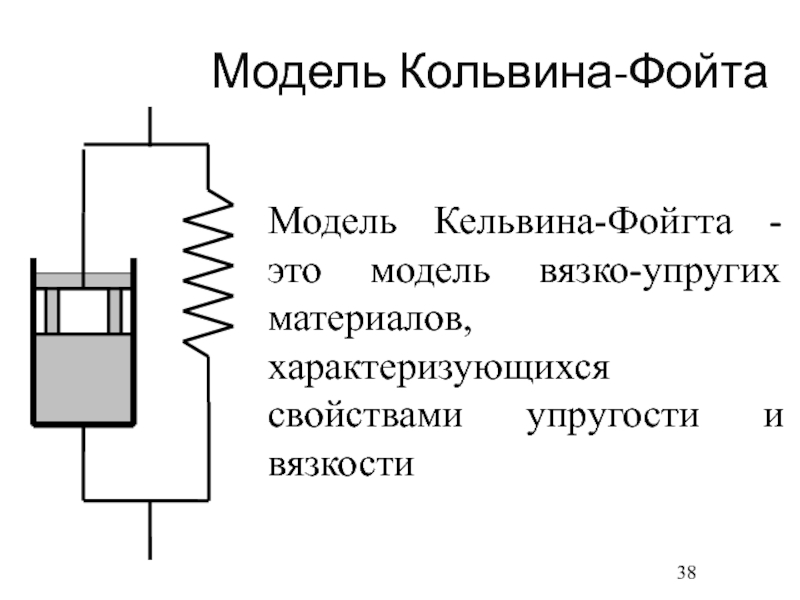
- 38. Модель Кольвина-Фойта Модель Кельвина-Фойгта - это модель вязко-упругих материалов, характеризующихся свойствами упругости и вязкости
- 39. Модель Пойтинга-Томпсона Рассмотренные нами ранее кривые ползучести
- 40. Со всеми реологическими свойствами в горных породах
- 41. ПРОЧНОСТЬ ГОРНЫХ ПОРОДПод термином "прочность породы" понимают
- 42. За величину предела прочности породы принимают величину напряжений, при которых происходит ее разрушение.
- 43. Nc, - величина разрушающей сжимающей силы при
- 44. Пределы прочности имеют размерность напряжений - Н/м2
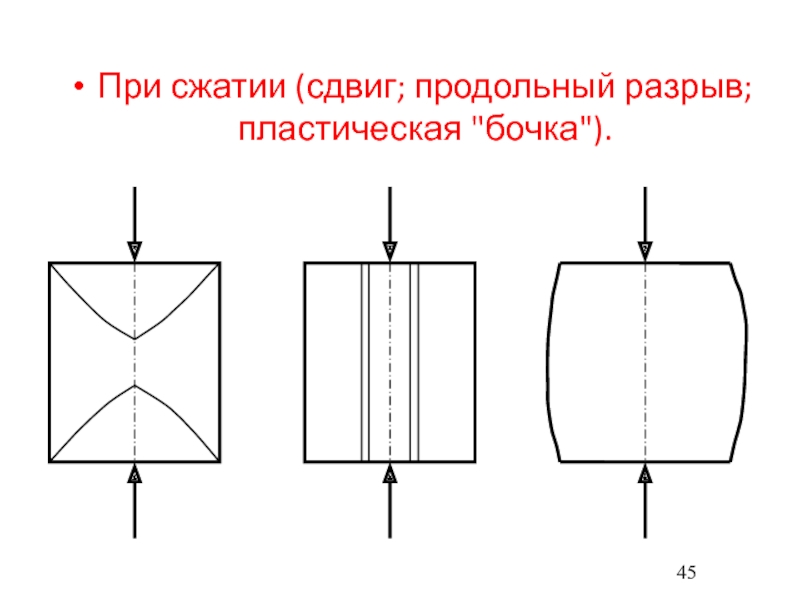
- 45. При сжатии (сдвиг; продольный разрыв; пластическая "бочка").
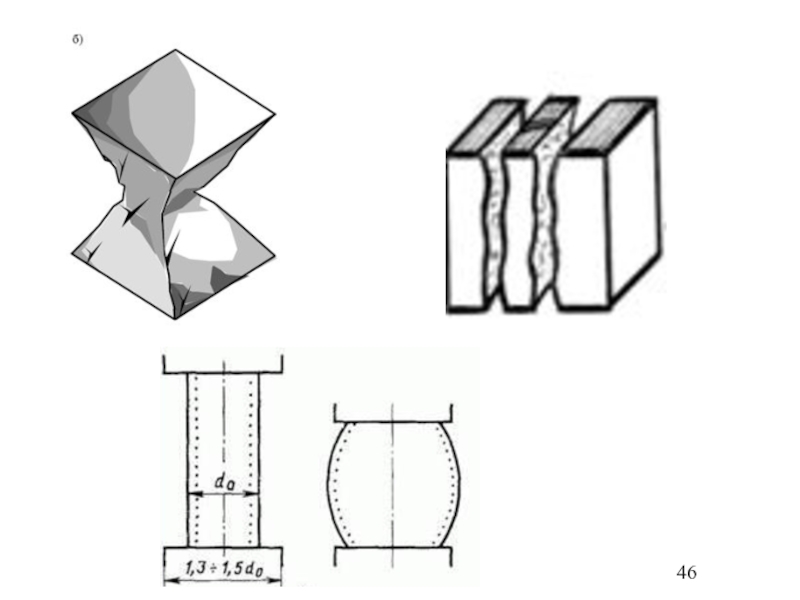
- 46. Слайд 46
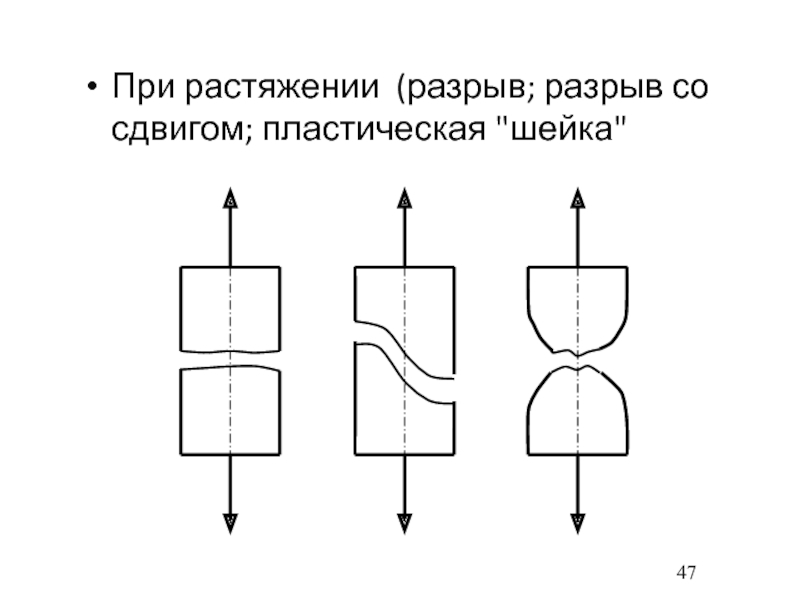
- 47. При растяжении (разрыв; разрыв со сдвигом; пластическая "шейка"
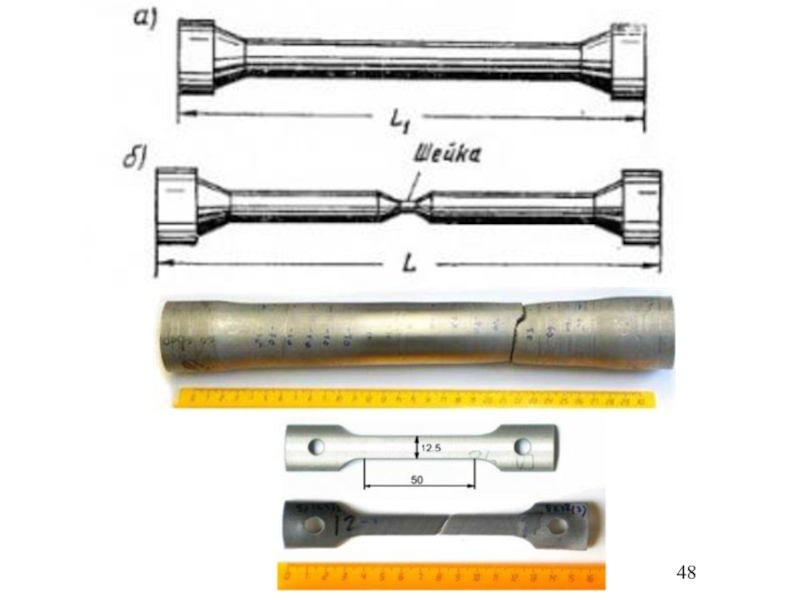
- 48. Слайд 48
- 49. Однако определенные таким способом характеристики не являются
- 50. Существует несколько теорий прочности. В основе каждой теории лежит свой критерий прочности
- 51. Теория нормальных напряжений Согласно теории, предложенной Галилеем,
- 52. Однако экспериментальные данные плохо согласуются с этой
- 53. Теория максимальных деформаций В 17 веке Сен-Венаном
- 54. Эта теория также не учитывает роли касательных
- 55. Теория максимальных касательных напряжений создана Кулоном. в
- 56. Слайд 56
- 57. Так как максимальные касательные напряжений при сложном напряженном состоянии равны:
- 58. то условие разрушения по этой теории будет следующим:
- 59. Эта теория прочности согласуется с экспериментальными данными
- 60. Ни одна из указанных теорий не учитывает
- 61. где 1, 2, 3 - напряжения по
- 62. Скачать презентанцию
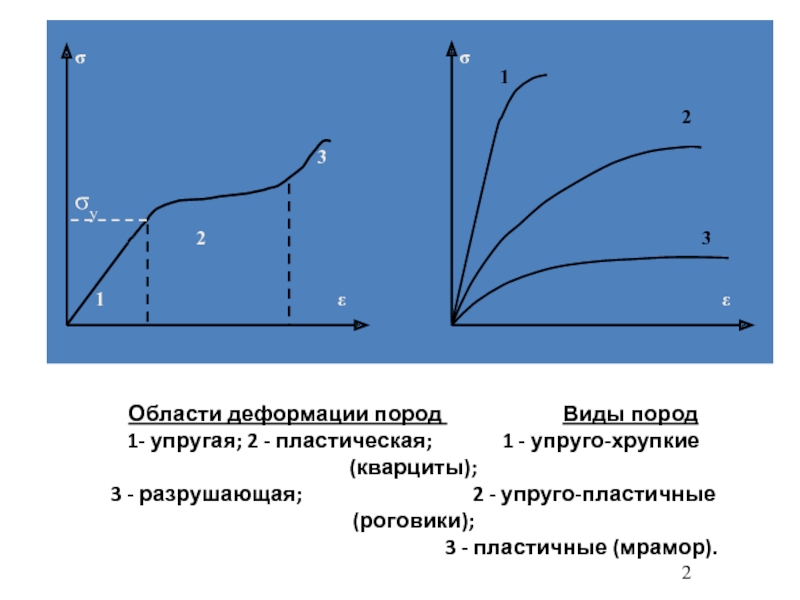
Области деформации пород Виды пород 1- упругая; 2 - пластическая; 1 - упруго-хрупкие (кварциты);
Слайды и текст этой презентации
Слайд 2Области деформации пород
Виды пород 1- упругая; 2 - пластическая;
1 - упруго-хрупкие (кварциты); 3 - разрушающая; 2 - упруго-пластичные (роговики); 3 - пластичные (мрамор).Слайд 3Выделяются две группы неразрушающих деформаций:
пластические деформации.
упругие деформации;
Характерной чертой
пластической деформации является ее необратимость. После снятия нагрузки - форма
и размеры образца полностью не восстанавливаются.Слайд 4Причины деформации
При изменении расстояния между атомами изменяются силы взаимодействия между
ними, которые стремятся вернуть тело в исходное состояния. Поэтому силы
упругости имеют электромагнитную природу.Слайд 5В случае упругих деформаций наблюдается прямая зависимость между напряжением и
соответствующей деформацией
С ростом величины упругой деформации в образце накапливается потенциальная
энергия, которая после прекращения действия внешних сил возвращает образец в исходное состояние. Максимальное напряжение, при котором еще не обнаруживаются остаточные деформации, называется пределом упругости данной породы.
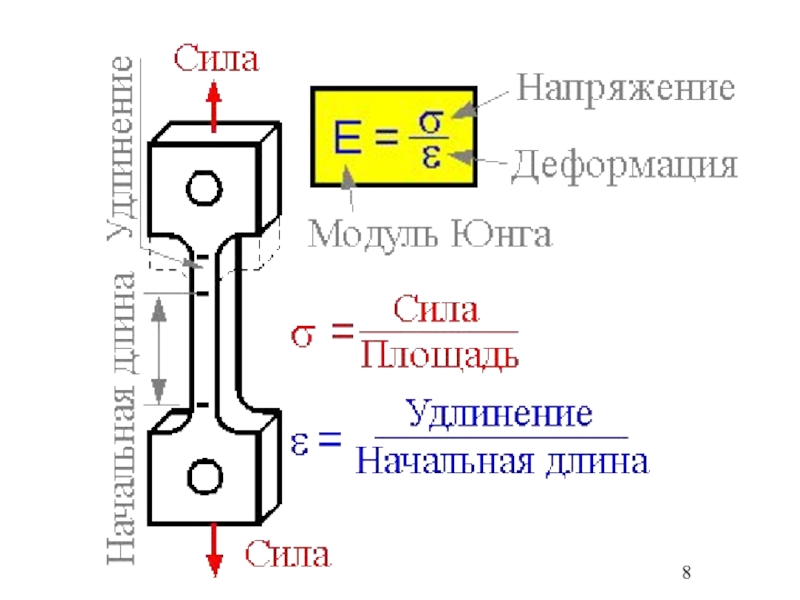
Слайд 7Коэффициент пропорциональности между действующим продольным напряжением (растягивающим или сжимающим) и
соответствующей ему относительной деформацией называется модулем продольной упругости (модуль Юнга):
Па (Н/м2).
Слайд 9Коэффициент пропорциональности между касательным напряжением и соответствующей ему относительной деформацией
сдвига носит название модуля сдвига:
Па (Н/м2).
Слайд 11На практике часто пользуются еще одним показателем упругости пород -
коэффициентом Пуассона.
В отличие от всех предыдущих, упругих параметров, он
является коэффициентом пропорциональности только между деформациями – относительными продольными
и
относительными поперечными:
Слайд 12В случае идеально упругих тел достаточно знать лишь модуль Юнга
и модуль сдвига, так как другие параметры могут быть вычислены
по определенным соотношениям теории упругости. Например, модуль сдвига:Слайд 13В условиях равномерного упругого трехосного сжатия породы наблюдается прямая пропорциональная
зависимость между действующим давлением и относительным изменением объема породы:
Слайд 14Соответствующий коэффициент пропорциональности (К) называется модулем объемного (всестороннего) сжатия. Он
так же связан с модулем продольной упругости и коэффициентом Пуассона
зависимостью:Слайд 15Обобщенная зависимость изменения модуля Юнга пород от пористости может быть
выражена формулой:
Слайд 16Пластичность
- свойство горной породы в результате силового воздействия давать
остаточные деформации без разрушения.
Слайд 18Коэффициент пластичности – отношение работы на разрушение образца реальной породы
к работе на разрушение идеально упругой породы:
Слайд 19Глинистые породы могут быть хрупкими, пластичными и текучими в зависимости
от влажности.
Эта зависимость от влажности характеризуется их пределами пластичности.
Пределы пластичности - это значения влажности породы (в %), при которых происходит переход породы из хрупкого состояния в пластическое и из пластического в текучее.
Слайд 20В первом случае, это значение влажности в %, при котором
происходит переход породы из хрупкого состояния в пластическое называется нижним
пределом пластичности - Wп .Значения влажности в %, при которых происходит переход из пластического состояния в текучее называется верхним пределом пластичности - Wт.
Слайд 21Wт – Wп = Ф
Разность верхнего и нижнего пределов пластичности
называется числом пластичности.
Оно характеризует диапазон влажности, в пределах которого порода
находится в пластическом состоянииСлайд 22Реология - наука о течении вещества («рео» в переводе означает «теку»)
Под реологическими параметрами понимают параметры, характеризующие изменение всех механических характеристик
породы при длительном воздействии на нее нагрузок, в том числе и не превышающих предела упругости.Слайд 23Реология устанавливает общие законы образования и развития деформаций во времени.
К
основным реологическим параметрам относятся:
Ползучесть
Релаксация напряжений
Длительная прочность
Слайд 24Ползучесть - это явление постепенного роста деформаций породы во времени
при постоянном напряжении.
Слайд 25Релаксацией напряжений - называется постепенное снижение напряжений в породе во
времени при постоянной деформации.
Слайд 27Время, в течение которого напряжение убывает в е раз (2,7)
называется временем релаксации.
где, σt - напряжения во времени;
σ0 - начальное
напряжение;t - время (текущая координата);
t0 - время релаксации, постоянное для данной породы.
Кривые релаксации напряжения описываются экспоненциальной зависимостью
Слайд 28Для характеристики релаксационной стойкости горной породы вводят относительный показатель падения
напряжений за определенный промежуток времени
где: σ0 - напряжение в образце
в момент деформации;σt - напряжение в образце по истечении определенного периода времени (сутки, неделю, месяц).
Слайд 29Опыт показывает, что при воздействии длительных напряжений происходит постепенное снижение
прочности горных пород.
Прочность соответствующая той или иной длительности воздействия
нагрузки, называется длительной прочностью.Слайд 30Длительная прочность пород с увеличением времени действия нагрузки падает по
определенной кривой, асимптотически приближаясь к некоторому определенному значению, называемому пределом
длительной прочности.Как правило для большинства горных пород предел длительной прочности равен:
σ∞=(0,7…0,8)· σсж
где, σсж - прочность породы при мгновенном нагружении.
Слайд 31Предел длительной прочности - это максимальное напряжение, при котором порода
никогда не разрушается.
Слайд 32Все реологические уравнения состояния пород моделируют с помощью идеальных тел,
которые служат довольно хорошим приближением к реальным телам. Они изучаются
в классической механике.Слайд 34Тело Ньютона
- идеально вязкое тело (поршень с отверстиями в цилиндре
заполненном вязкой жидкостью)
ньютоновская вязкая жидкость
τ=η·έ= η·(dε/dt) η – вязкость
(коэффициент внутреннего трения - который является коэффициентом пропорциональности между приложенными касательными напряжением и скоростью деформирования)
Слайд 35Тело Сен-Венана
- абсолютно пластичное тело (модель сухого трения тяжелого тела,
лежащего на горизонтальном основании и сдвигаемого внешними силами). Смещение возможно
лишь при достижении внешними силами определенной величины(σ> σ*)
Слайд 36Путем соответствующих комбинаций этих простых тел могут быть получены сложные
модели для описания сложных деформаций
упруго-пластичных,
вязко-пластичных горных пород.
Слайд 37Модель Максвелла
поведение глин хорошо описывается реологической моделью
"тела Максвелла", представляющего собой последовательное соединение "тела Гука" и "тела
Ньютона"Слайд 38Модель Кольвина-Фойта
Модель Кельвина-Фойгта - это модель вязко-упругих материалов, характеризующихся
свойствами упругости и вязкости
Слайд 39Модель Пойтинга-Томпсона
Рассмотренные нами ранее кривые ползучести для твердых тел
довольно хорошо описываются реологической моделью "линейного стандартного тела".
Такая модель
представляет собой сочетание "тела Гука" и "ньютоновской вязкой жидкости", соединенных следующим образом ": тело Гука" и "ньютоновская жидкость" соединены последовательно и к ним еще раз параллельно присоединено "тело Гука".Слайд 40Со всеми реологическими свойствами в горных породах мы встречаемся при
строительстве и эксплуатации различных подземных сооружений, при ведении открытых горных
работ, строительстве фундаментов, зданий и др. сооружений -там где наблюдается длительное воздействие нагрузок.Слайд 41ПРОЧНОСТЬ ГОРНЫХ ПОРОД
Под термином "прочность породы" понимают ее способность сопротивляться
различным по интенсивности и характеру силовым воздействиям, не разрушаясь.
Различают пределы
прочности на сжатие,
растяжение,
сдвиг,
изгиб,
кручение и т.д.
Слайд 42За величину предела прочности породы принимают величину напряжений, при которых
происходит ее разрушение.
Слайд 43Nc, - величина разрушающей сжимающей силы при которой происходит разрушение
породы, Н;
Np, - величина разрушающей растягивающей силы при которой происходит
разрушение породы, Н;A0 - исходное поперечное сечение испытуемого образца, м2.
Слайд 44Пределы прочности имеют размерность напряжений - Н/м2 (Па, МПа).
В зависимости
от типа породы возможны следующие виды разрушения испытываемых образцов:
Сдвиг
Продольный разрыв
Пластическая
«бочка»Слайд 49Однако определенные таким способом характеристики не являются истинными для данного
типа породы.
Число факторов, влияющих на абсолютную величину этих характеристик
так велико, что последние могут рассматриваться только как относительные показатели, позволяющие производить сопоставление различных типов пород по их прочности. Слайд 51Теория нормальных напряжений
Согласно теории, предложенной Галилеем, разрушение материала наступает
тогда, когда наибольшее нормальное напряжение достигнет некоторого предельного значения, (предела
прочности либо одноосному сжатию, либо одноосному растяжению).Слайд 52Однако экспериментальные данные плохо согласуются с этой теорией, так как
она не учитывает касательных напряжений.
Если в образце развиваются и
касательные напряжения, то образец разрушается раньше, чем нормальные напряжения достигнут максимальной величины.Слайд 53Теория максимальных деформаций
В 17 веке Сен-Венаном была сформулирована теория
прочности, согласно которой, разрушение материала произойдет тогда, когда наибольшие относительные
деформации станут равными некоторому предельному значению при сжатии:Слайд 54Эта теория также не учитывает роли касательных напряжений в процессах
разрушения материала, и поэтому в ряде случаев она не согласовывалась
с данными экспериментов.Она более подходит при описании хрупкого разрушения породы
Слайд 55Теория максимальных касательных напряжений
создана Кулоном.
в качестве критерия разрушаемости
материала он принял максимальные касательные напряжения:
Шарль Огюсте́н де Куло́н
Слайд 59Эта теория прочности согласуется с экспериментальными данными для материалов, разрушение
которых происходит в зоне пластического течения.
Слайд 60Ни одна из указанных теорий не учитывает комплексного влияния всех
видов напряжений на процесс разрушения.
Максвелл предложил теорию прочности, в
основу которой положил величину работы по изменению формы образца при его деформировании без изменения объема.Была разработана энергетическая теория прочности.
Условие разрушения в ней выражается через нормальные напряжения: