Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика реального кристалла
Содержание
- 1. Физика реального кристалла
- 2. Наблюдение дислокаций
- 3. Фотоупругость
- 4. Слайд 4
- 5. Слайд 5
- 6. Метод фотоупругостиРастяжение Сжатие
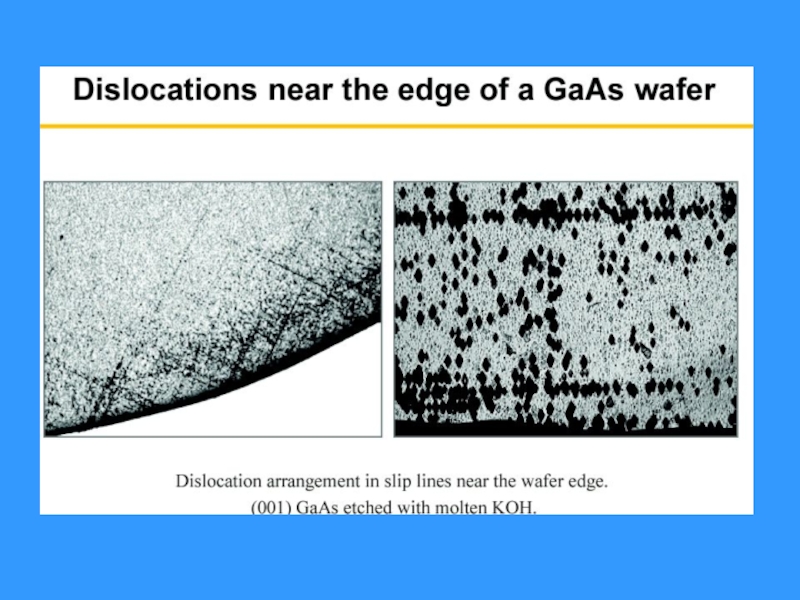
- 7. Дислокационные ямки травления
- 8. Слайд 8
- 9. Слайд 9
- 10. Избирательное травление
- 11. Декорирование
- 12. Дифракция рентгеновских лучей (электронов, нейтронов) на периодических
- 13. Дифракция по Лауэ (белое излучение)Доказательство волновой природы рентгеновских лучей- дифракция на атомарнойкристаллической решетке
- 14. Дисперсионные соотношения для частицФотоны Е
- 15. Прямая и обратная решетки кристаллов
- 16. Сфера Эвальдаq = k’ - k -
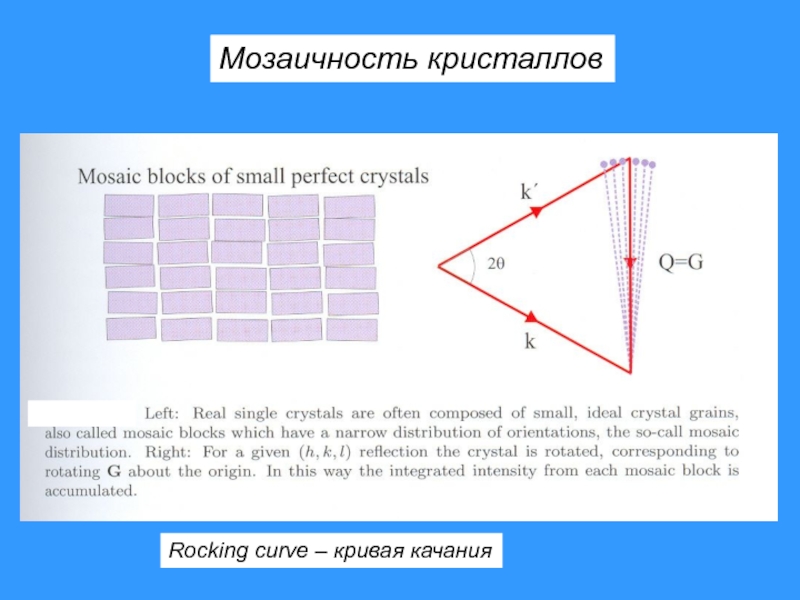
- 17. Мозаичность кристалловRocking curve – кривая качания
- 18. Соответствие между выходом дислокацийи ямками травления
- 19. Слайд 19
- 20. Задача!
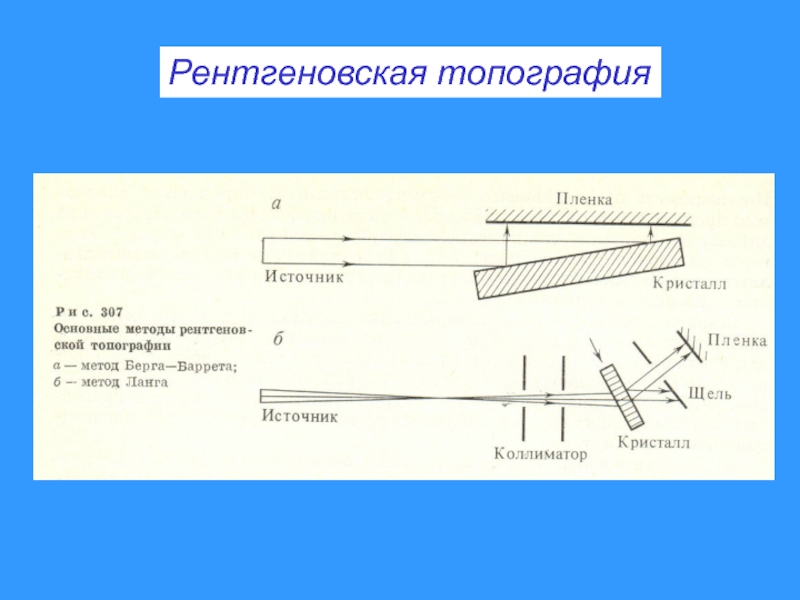
- 21. Рентгеновская топография
- 22. Слайд 22
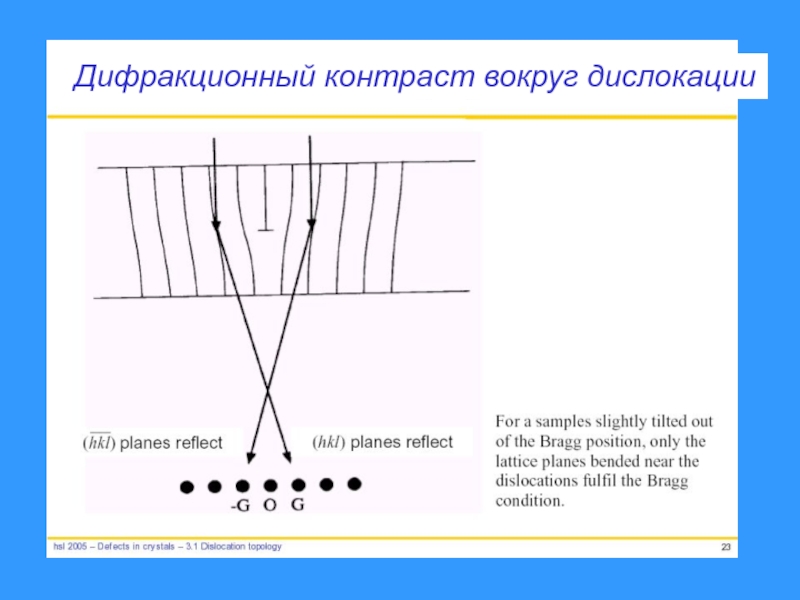
- 23. Дифракционный контраст вокруг дислокации
- 24. Слайд 24
- 25. Слайд 25
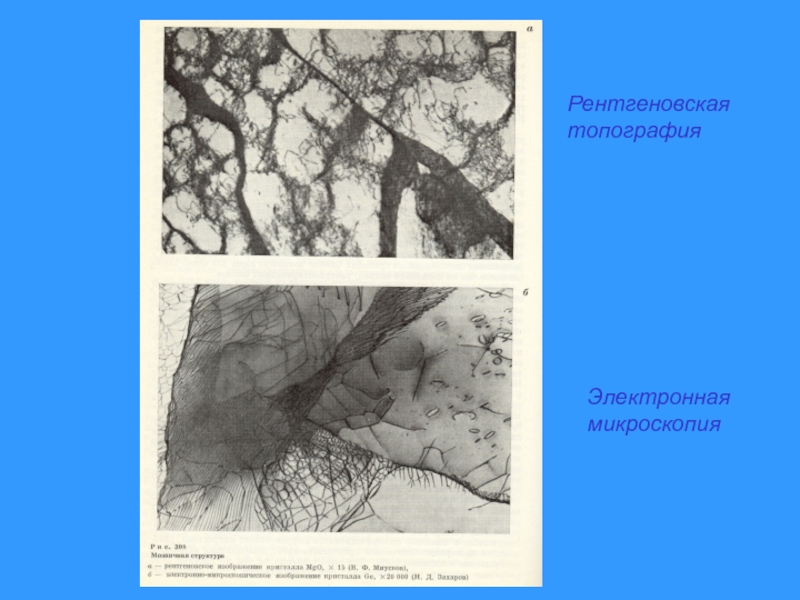
- 26. Рентгеновская топография и электронная микроскопия
- 27. Рентгеновская топографияЭлектронная микроскопия
- 28. Слайд 28
- 29. Слайд 29
- 30. Разного рода микроскопия
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. u = (b/2)
- 38. Слайд 38
- 39. В этом случае дифракцияне наблюдаетсяДифракционный контраст имеет
- 40. g = k’ - k - вектор
- 41. (a) A TEM picture of dislocation structure
- 42. Пластическая деформация и упрочнение кристаллов
- 43. Слайд 43
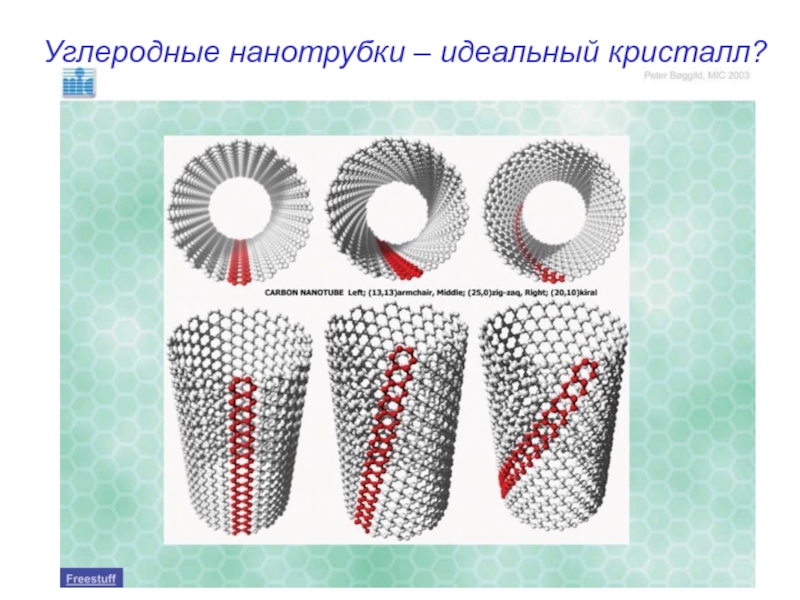
- 44. Углеродные нанотрубки – идеальный кристалл?
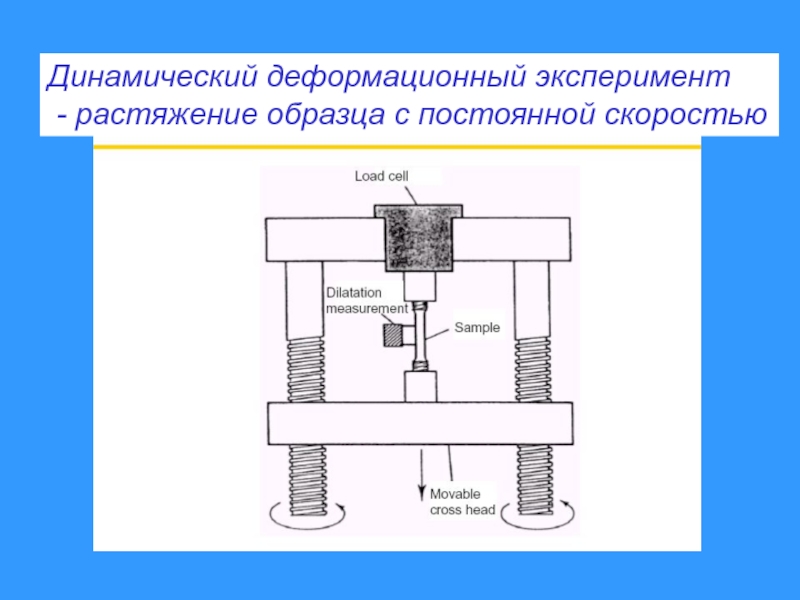
- 45. Динамический деформационный эксперимент - растяжение образца с постоянной скоростью
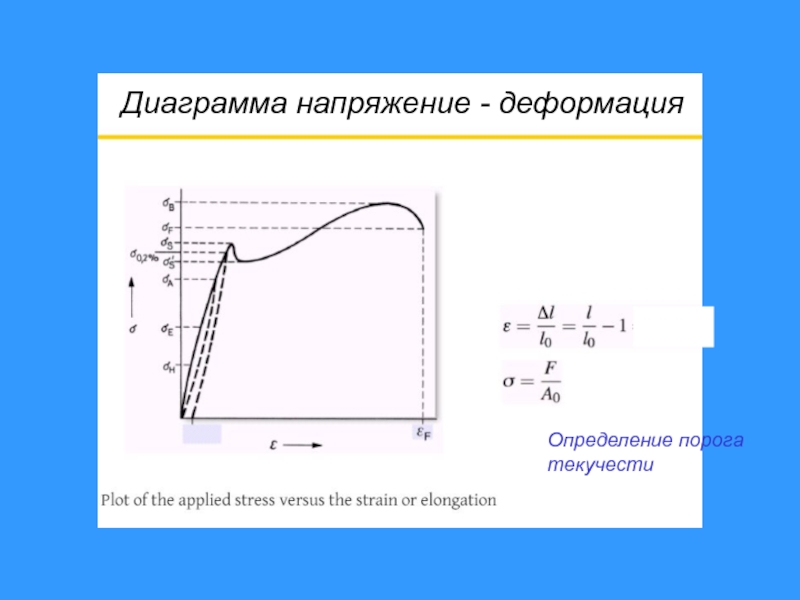
- 46. Диаграмма напряжение - деформацияОпределение порогатекучести
- 47. Эксперимент на растяжение
- 48. Пластичный кристаллХрупкий кристалл –-слишком мало дислокаций,или высокие барьеры Пайерлсаразрушение кристаллаполикристаллымонокристаллы
- 49. Размножение и движениедислокацийВзаимодействие+ торможение дислокацийупрочнениекристаллаУпрочнение монокристалловd/d = -коэффициентупрочнения
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
- 53. Дислокации леса
- 54. К вычислению пластическойдеформации = b
- 55. деформации ~ Gb/r Gb/ Gb1/2
- 56. = bПараболический закон упрочнения
- 57. d/d = -коэффициентупрочнения
- 58. Упрочнение в сплавах(одно из важнейших достижений современной
- 59. Слайд 59
- 60. Слайд 60
- 61. Преодоление дислокациями препятствий
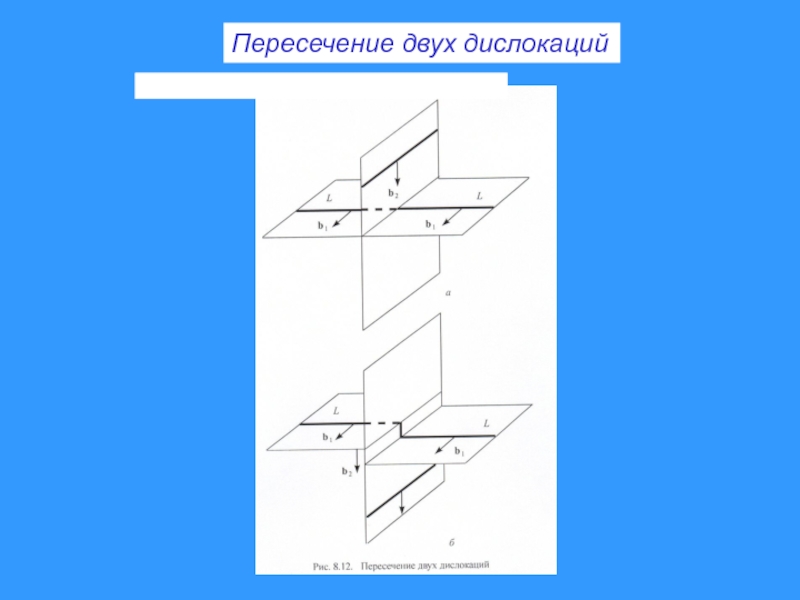
- 62. Пересечение двух дислокаций
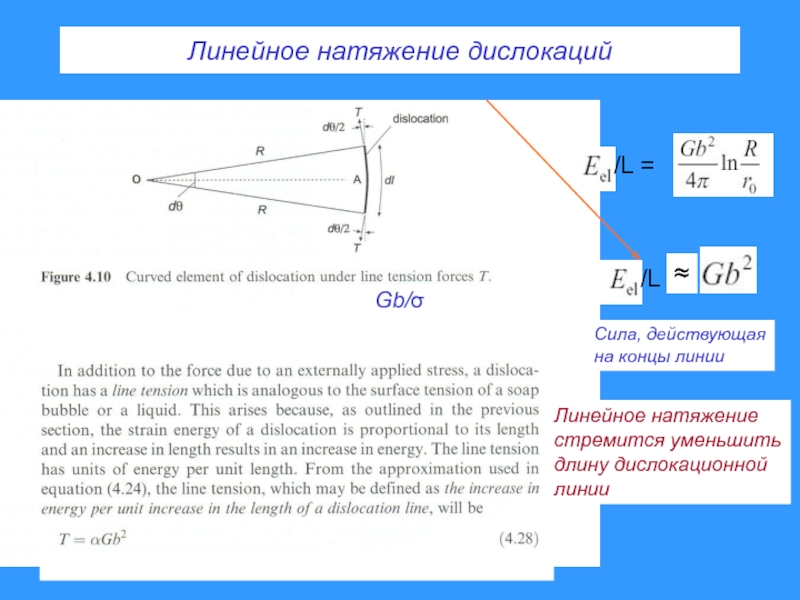
- 63. Линейное натяжение дислокаций/L = /L = Линейное натяжениестремится уменьшитьдлину дислокационнойлинииСила, действующаяна концы линииGb/
- 64. Преодоление точечных препятствий
- 65. R = Gb/;R L/2, следовательно:
- 66. Слайд 66
- 67. Механизм упрочнения в сплавах =10b;
- 68. Физика легирования
- 69. Зоны Гинье- Престона
- 70. Плоские скопления точечных дефектов
- 71. Сплав«Дюралюминий»- 4% меди
- 72. Слайд 72
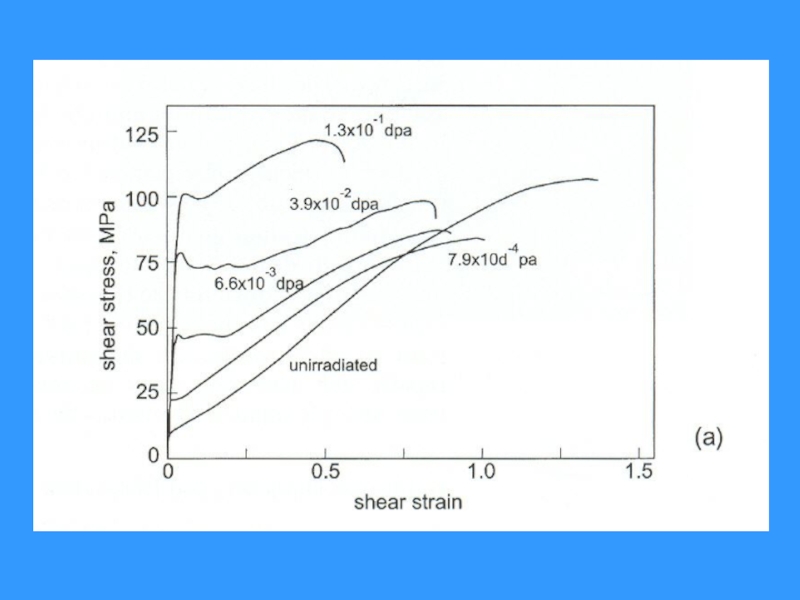
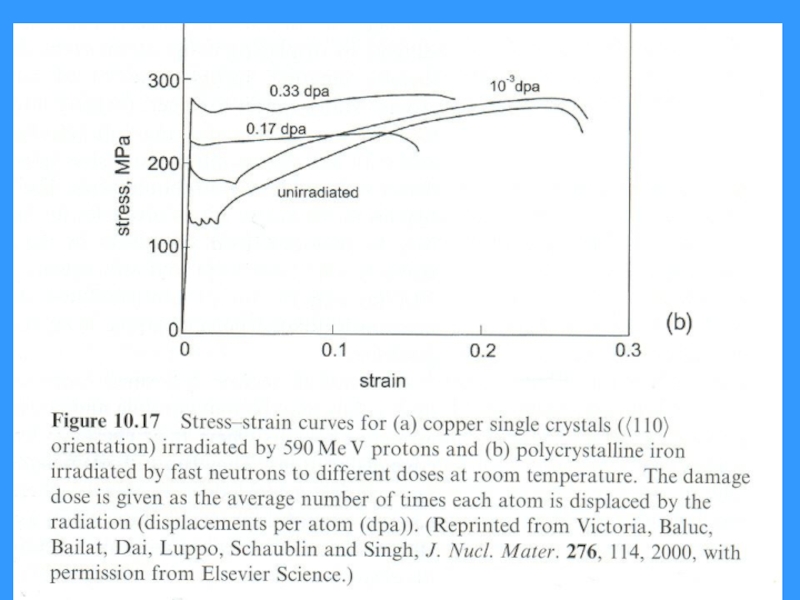
- 73. Радиационное упрочнение
- 74. Слайд 74
- 75. Слайд 75
- 76. Необходимо все проверять, все оспаривать. Знание, добытое
- 77. Слайд 77
- 78. Скачать презентанцию
Наблюдение дислокаций
Слайды и текст этой презентации
Слайд 1Профессор Б.И.Островский
Физика реального кристалла
ostr@cea.ru
14. Методы наблюдения дислокаций.
Пластическая
деформация и
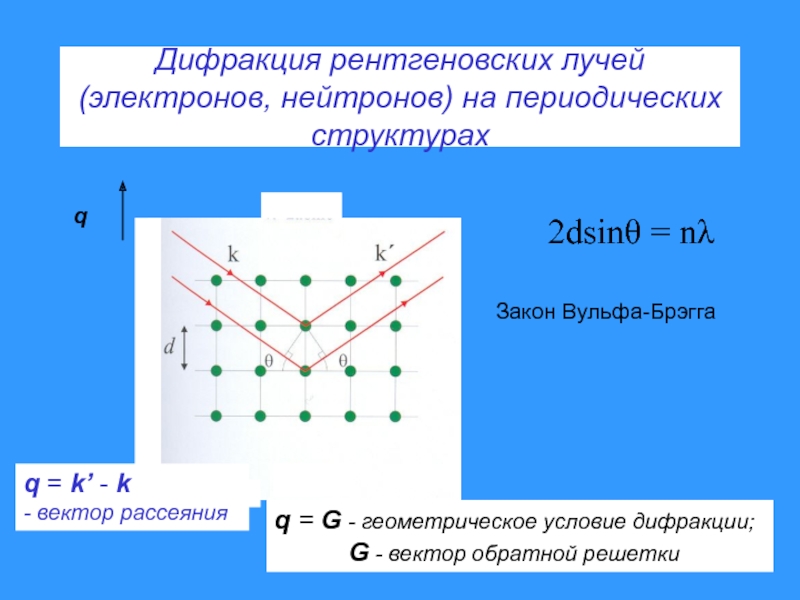
Слайд 12Дифракция рентгеновских лучей (электронов, нейтронов) на периодических структурах
2dsin
= n
Закон Вульфа-Брэгга
q
q = k’ - k
- вектор рассеяния
q =
G - геометрическое условие дифракции;G - вектор обратной решетки
Слайд 13Дифракция по Лауэ
(белое излучение)
Доказательство волновой
природы рентгеновских лучей
- дифракция на
атомарной
кристаллической решетке
Слайд 14Дисперсионные соотношения для частиц
Фотоны Е = ћ =
h = hc/ ; p = ћk
Де Бройль (1925):
p = ћk ; p = mv ; k = 2 / = h/mv
Электроны Е = Ек =p2/2m = h2/2me 2
=1A, E 100 ev
Для дифракционных исследований пространственной структуры
вещества используют сейчас, как правило, рентгеновские лучи в
диапазоне длин волн от 0.5 до 10 А, пучки тепловых нейтронов
(от 1 до 10 А) и быстрых электронов (от 0.05 до 1 А).
; E ;p
E ;p ;k
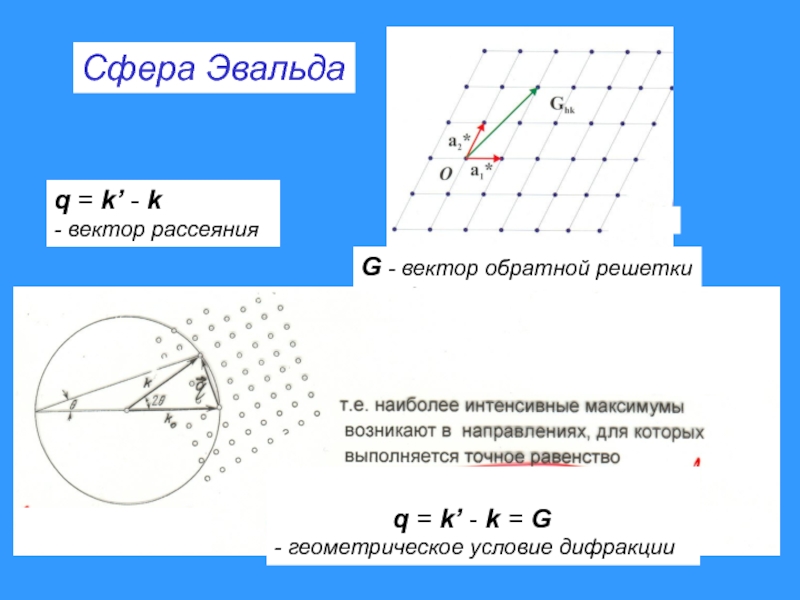
Слайд 16Сфера Эвальда
q = k’ - k
- вектор рассеяния
- геометрическое условие дифракции
G - вектор обратной решетки
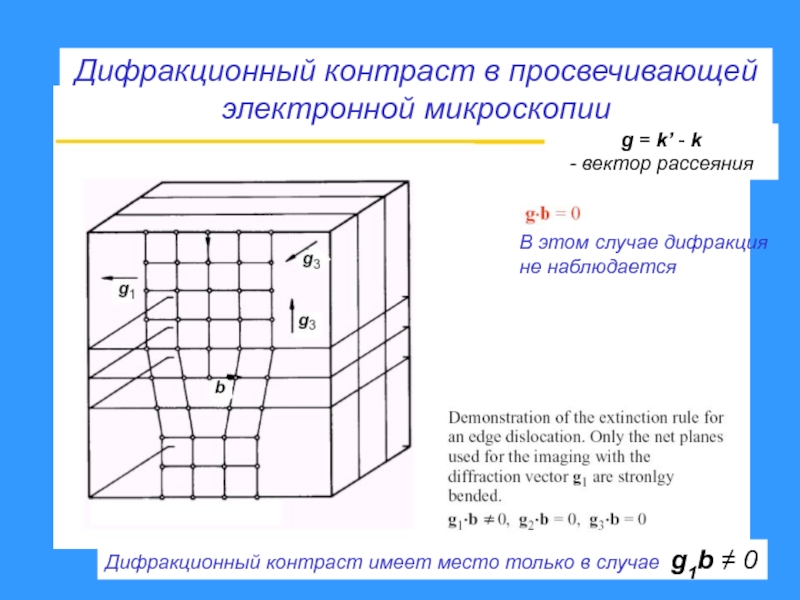
Слайд 39В этом случае дифракция
не наблюдается
Дифракционный контраст имеет место только в
случае g1b 0
g = k’ - k
- вектор
рассеянияДифракционный контраст в просвечивающей
электронной микроскопии
Слайд 40g = k’ - k
- вектор рассеяния
Изменение направления
вектора рассеяния
g при
изучении одного и того
же участка кристалла
выявляет различные
системы
дислокаций!
Слайд 41(a) A TEM picture of dislocation structure in pure single
crystal BCC molybdenum deformed at temperature 278K (courtesy of L.
L. Hsiung).(b) Dislocations formed bundles (braids) in single crystal copper deformed at77K
(c) Dislocation structure formed in single crystal BCC molybdenum deformed
at temperature 500K (courtesy of L. L. Hsiung). The dark regions contain a
high density of entangled dislocations lines that can no longer be distinguished
individually.
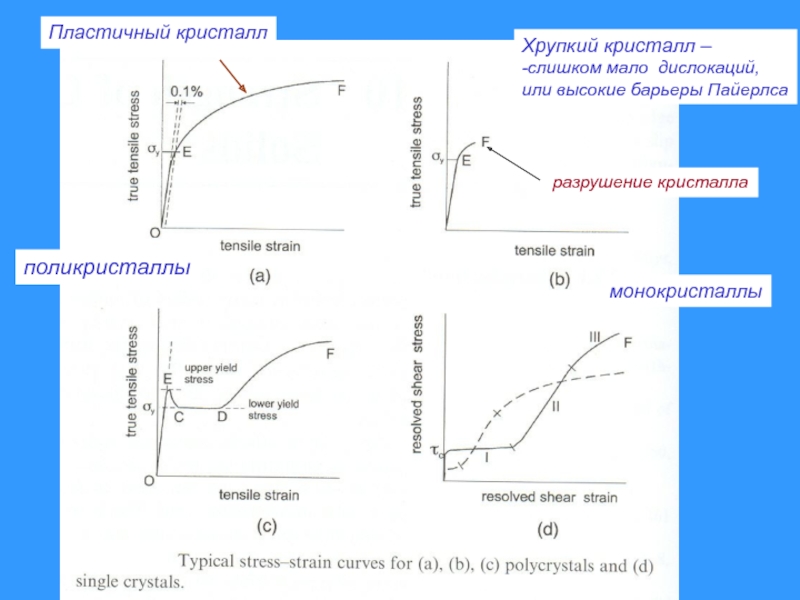
Слайд 48Пластичный кристалл
Хрупкий кристалл –
-слишком мало дислокаций,
или высокие барьеры Пайерлса
разрушение кристалла
поликристаллы
монокристаллы
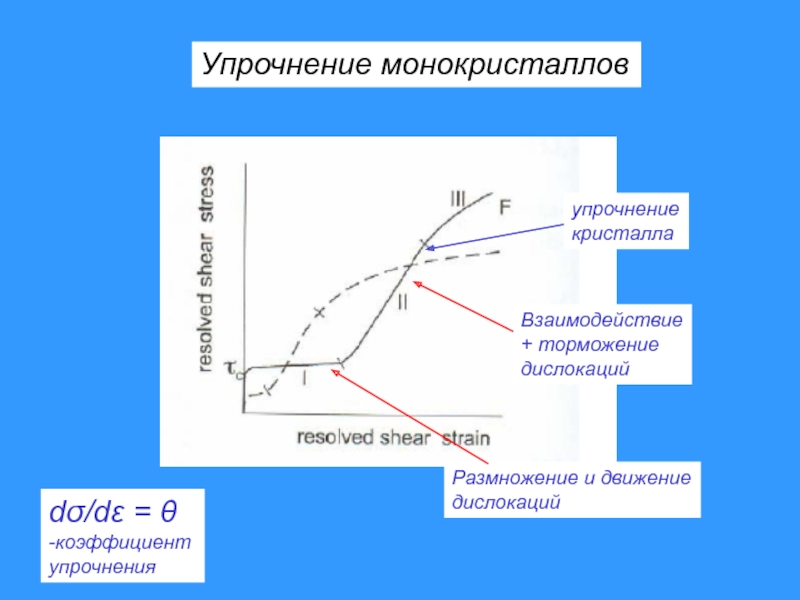
Слайд 49Размножение и движение
дислокаций
Взаимодействие
+ торможение
дислокаций
упрочнение
кристалла
Упрочнение монокристаллов
d/d =
-коэффициент
упрочнения
Слайд 58Упрочнение в сплавах
(одно из важнейших достижений
современной цивилизации)
Увеличение порога текучести
таких металлов
как Al , Cu, Ni в сто и более
раз за счет правильного выбора легирующих элементов и оптимизации
термической обработки !
Слайд 63Линейное натяжение дислокаций
/L =
/L =
Линейное натяжение
стремится уменьшить
длину дислокационной
линии
Сила,
действующая
на концы линии
Gb/
Слайд 65R = Gb/;
R L/2,
следовательно:
Gb/L ,
и
напрямую зависит
от расстояний
между стопорами
U0 Gb2
Задача!
Слайд 67Механизм упрочнения в сплавах
=10b; G/10
теоретический
предел!
Стопоры в
плоскости
скольжения
Притяжение за счет сил Пича –Келлера b, и вследствие разных знаков отрезков дислокаций
b
Слайд 76Необходимо все проверять, все оспаривать. Знание,
добытое без личного усилия,
без личного напряжения,
знание мертвое. Только пропущенное через
собственную
голову становится твоим достоянием.
