Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Раскрываем секреты линейной функции и ее графика
Содержание
- 1. Раскрываем секреты линейной функции и ее графика
- 2. Общие итоги работ: Если угловые коэффициенты у
- 3. y = 2 xy =
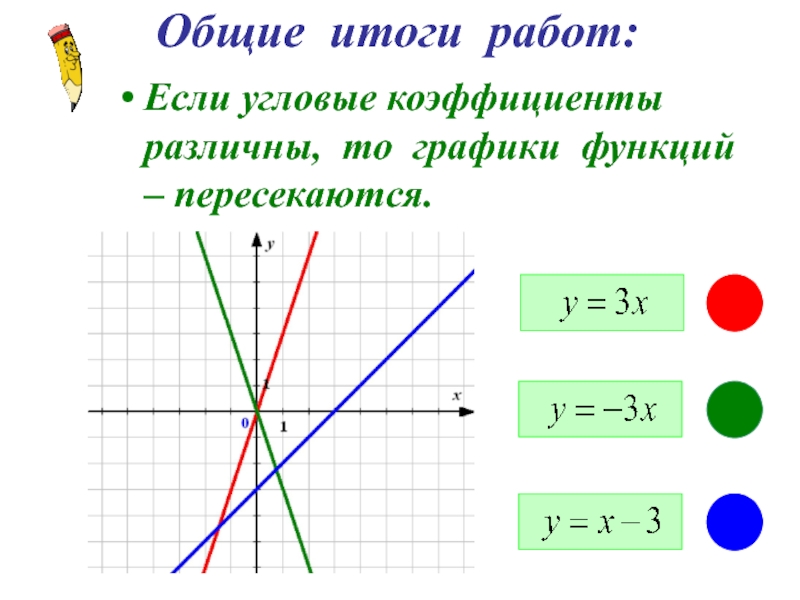
- 4. Если угловые коэффициенты различны, то графики функций – пересекаются.Общие итоги работ:
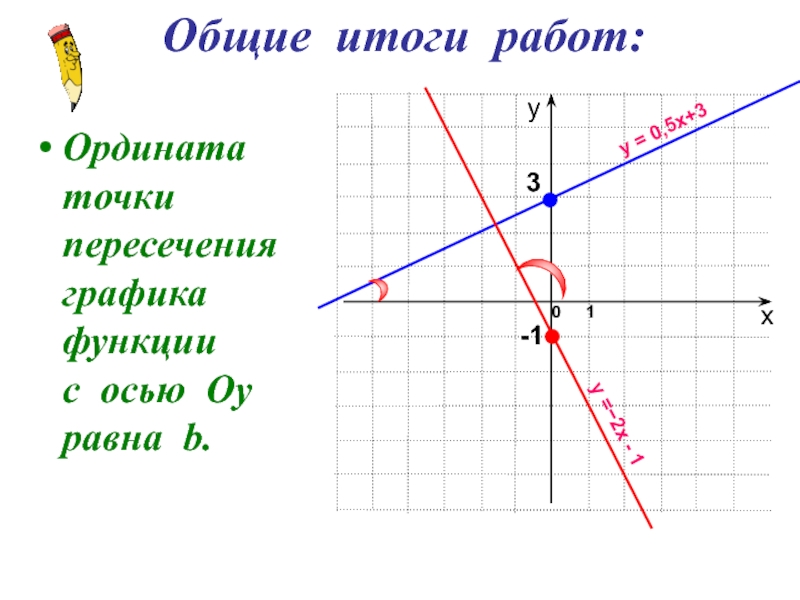
- 5. Общие итоги работ: Ордината точки пересечения графика
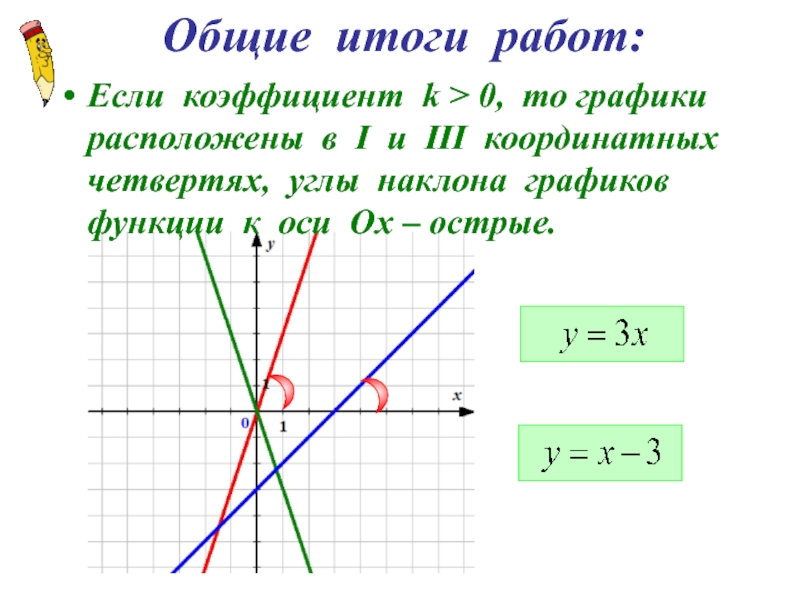
- 6. Общие итоги работ: Если коэффициент k >
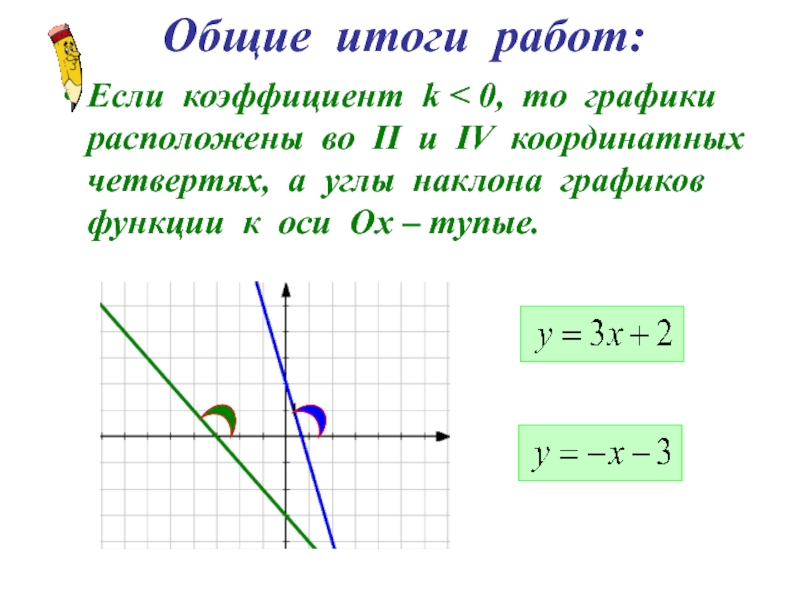
- 7. Общие итоги работ: Если коэффициент k <
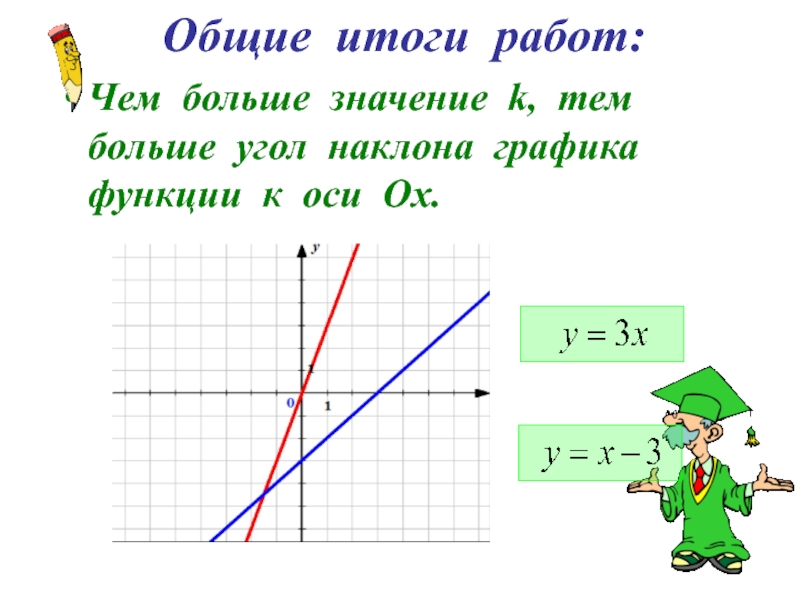
- 8. Общие итоги работ: Чем больше значение k, тем больше угол наклона графика функции к оси Ох.
- 9. Скачать презентанцию
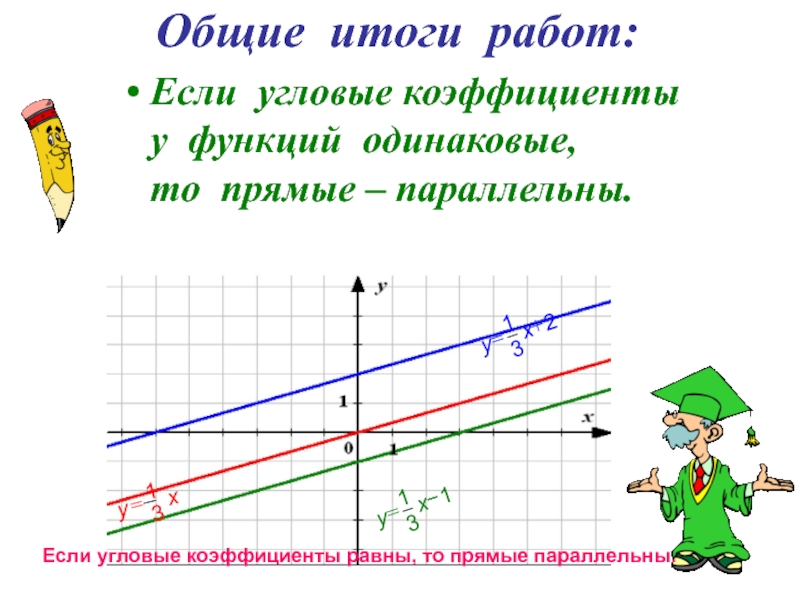
Общие итоги работ: Если угловые коэффициенты у функций одинаковые, то прямые – параллельны. Если угловые коэффициенты равны, то прямые параллельны.
Слайды и текст этой презентации
Слайд 3 y = 2 x
y = 2x
y = 2
x +3
y =2x+3
(0 ; ), (- 2;
)(0 ; ), ( - 4 ; )
0
- 4
3
- 5
y = 2 x – 4
y = 2x – 4
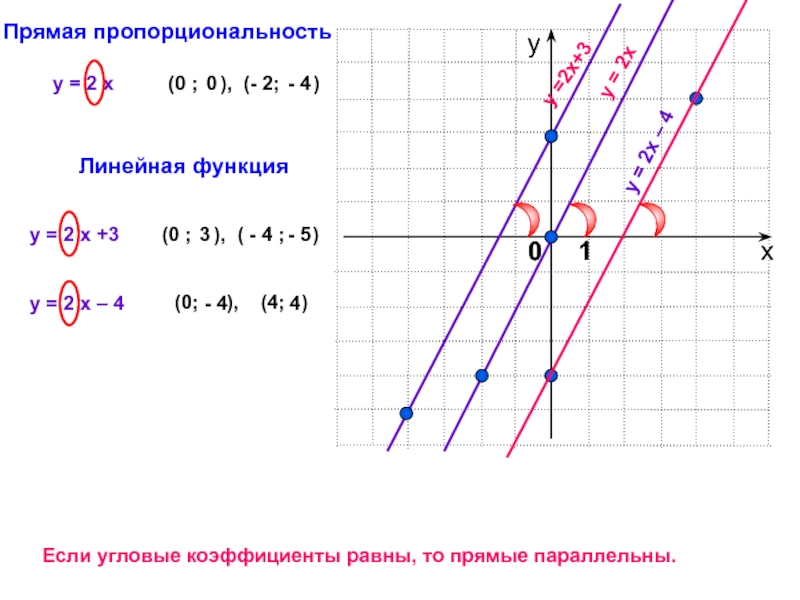
Если угловые коэффициенты равны, то прямые параллельны.
Прямая пропорциональность
(0; ), (4; )
- 4
4
Линейная функция
1
0
Слайд 5Общие итоги работ:
Ордината точки пересечения графика функции
с осью Оу
равна b.
y = 0,5x+3
y =−2х - 1
0 1
-1
3
Слайд 6Общие итоги работ:
Если коэффициент k > 0, то графики
расположены в I и III координатных четвертях, углы наклона графиков
функции к оси Ох – острые.
Слайд 7Общие итоги работ:
Если коэффициент k < 0, то графики
расположены во II и IV координатных четвертях, а углы наклона
графиков функции к оси Ох – тупые.
