Floyd– Warshall algorithm

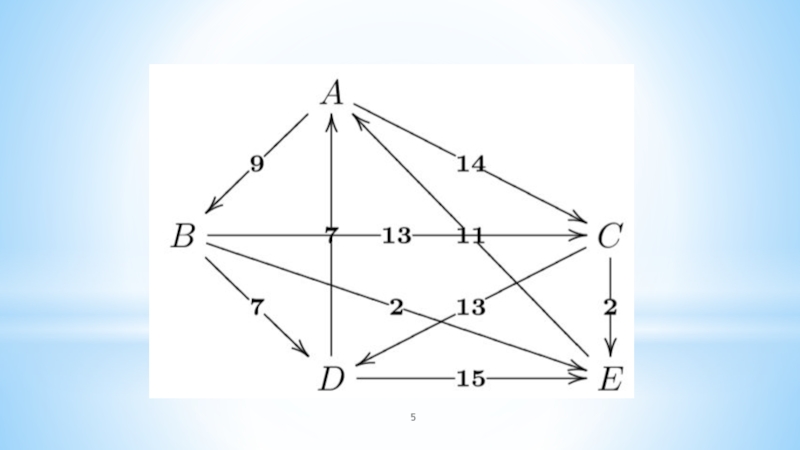
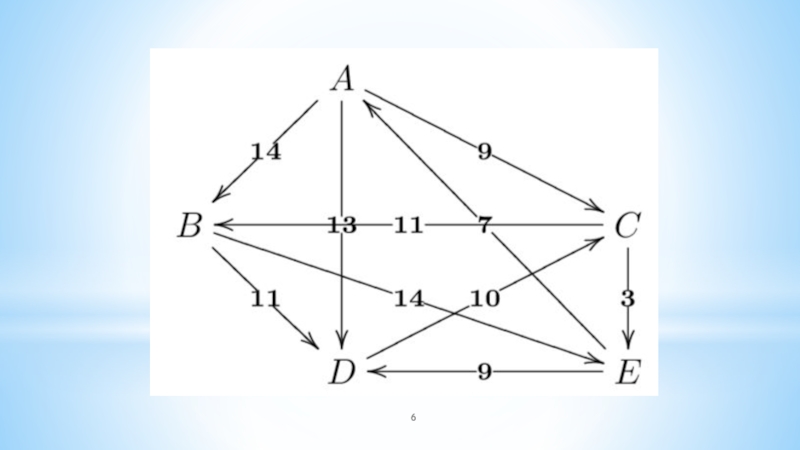
in a weighted graph with positive or negative edge weights

(but with no negative cycles/
Pseudocode for this basic version follows:

1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
2 for each edge (u,v)
3 dist[u][v] ← w(u,v) // the weight of the edge (u,v)
4 for each vertex v
5 dist[v][v] ← 0
6 for k from 1 to |V|
7 for i from 1 to |V|
8 for j from 1 to |V|
9 if dist[i][j] > dist[i][k] + dist[k][j]
10 dist[i][j] ← dist[i][k] + dist[k][j]
11 end if

0 above, the only known paths correspond to the single edges

in the graph.
At k = 1, paths that go through the vertex 1 are found: in particular, the path [2,1,3] is found, replacing the path [2,3] which has fewer edges but is longer (in terms of weight).
At k = 2, paths going through the vertices {1,2} are found. The red and blue boxes show how the path [4,2,1,3] is assembled from the two known paths [4,2] and [2,1,3] encountered in previous iterations, with 2 in the intersection. The path [4,2,3] is not considered, because [2,1,3] is the shortest path encountered so far from 2 to 3.
At k = 3, paths going through the vertices {1,2,3} are found.
Finally, at k = 4, all shortest paths are found.

three pairwise acquaintances, or three pairwise unfamiliar ones.
2. In the

graph in each vertex includes three edges. Prove that there is at least one cycle in the graph.
3. On the plane, 100 circles are given, constituting a connected (i.e., non-disintegrating) figure. Prove that this figure can be drawn without taking the pencil from the paper and not drawing the same line twice. Example of figure, that we can’t draw under this condition:

the chess knight , having visited each one once.

5. What

is the greatest number of chess queens that can be placed on an 8x8 board, so that no two are on the same horizontal, vertical or diagonal?

6. In the company of 2n + 1 people for any n people there is a different person from them who is familiar with each of them. Prove that in this company there is a person who knows everyone.

7. Among the participants of the conference, everyone has at least one friend. Prove that the participants can be distributed in two rooms so that each participant has a friend in the other room.

the minimum value, swaps it with the value in the

first position, and repeats these steps for the remainder of the list. Selection sort is noted for its simplicity, and also has performance advantages over more complicated algorithms in certain situations.

Insertion sort is a simple sorting algorithm that is relatively efficient for small lists and mostly sorted lists, and is often used as part of more sophisticated algorithms. It works by taking elements from the list one by one and inserting them in their correct position into a new sorted list. In arrays, the new list and the remaining elements can share the array's space, but insertion is expensive, requiring shifting all following elements over by one.

lists into a new sorted list. It starts by comparing

every two elements (i.e., 1 with 2, then 3 with 4...) and swapping them if the first should come after the second. It then merges each of the resulting lists of two into lists of four, then merges those lists of four, and so on; until at last two lists are merged into the final sorted list.

individual digits. n numbers consisting of k digits each are

sorted in O(n · k) time. Radix sort can process digits of each number either starting from the least significant digit or starting from the most significant digit. The algorithm first sorts the list by the least significant digit while preserving their relative order using a stable sort. Then it sorts them by the next digit, and so on from the least significant to the most significant, ending up with a sorted list.

Bucket sort is a divide and conquer sorting algorithm that generalizes counting sort by partitioning an array into a finite number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm.
A bucket sort works best when the elements of the data set are evenly distributed across all buckets.