Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формула Тейлора
Содержание
- 1. Формула Тейлора
- 2. Брук Тейлор (Taylor) (1685 -
- 3. Многочлен Тейлора.ОПРЕДЕЛЕНИЕ. Многочленом Тейлора степени n функции
- 4. Определение формулы Тейлора. ОПРЕДЕЛЕНИЕ. Формула вида f(x) =
- 5. Формула Тейлора с остатком в форме Лагранжа.
- 6. Введем вспомогательную функцию g(x) = (x -
- 7. Формула Тейлора с остатком в форме Пеано.ТЕОРЕМА
- 8. Доказательство. Так как f(x) n раз дифференцируема
- 9. Джузеппе Пеано (1858-1932). Итальянский математик и логик.
- 10. Единственность представления функции f(x) в виде многочлена
- 11. Доказательство. Для функции f(x) выполнены условия теоремы 2,
- 12. Разложение основных элементарных функций по формуле Тейлора. Если
- 13. f(x) = ех f (k)(x) =
- 14. f(x) = sinx f (k)(x)= sin(x
- 15. f(x) = ln(1+x). f (k)(x) = (-1)k-1(k-1)!(1
- 16. ПРИМЕРЫ.Разложить по формуле Маклорена до о(хn) функцию f(x).1)2)3)
- 17. Спасибо за внимание!misis.ru
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 3.5
Формула Тейлора
Формула Тейлора с остатком в форме
Лагранжа и в форме Пеано
по формуле Тейлора.Слайд 2Брук Тейлор (Taylor)
(1685 - 1731)
Английский математик. Родился в
предместье Лондона. Получил прекрасное домашнее музыкальное и художественное образование. В
15 лет поступил в Кембриджский университет, где незадолго до этого работал И.Ньютон, остававшийся кумиром молодых математиков, среди которых был и Брук Тейлор. В 1712г. Тейлора избрали членом Королевского общества. В 1718г. он уходит с поста секретаря общества, чтобы освободить время для философской работы.Тейлор исследовал свойства функций. В 1712г. нашел, в 1715г. опубликовал общую формулу разложения функций в степенной ряд, которая носит теперь его имя.
Слайд 3Многочлен Тейлора.
ОПРЕДЕЛЕНИЕ.
Многочленом Тейлора степени n функции f(x) в точке
х0 называется
многочлен следующего вида:
где по определению 0! = 1,
f (0)(x) = f(x).ЛЕММА.
Доказательство.
Из формулы (1) следует, что Tn(x0) = f(x0). Продифференцировав (1),
получим Tn′(x0) = f '(x0), и т.д.
Слайд 4Определение формулы Тейлора.
ОПРЕДЕЛЕНИЕ.
Формула вида
f(x) = Tn(x) + Rn(x)
называется формулой Тейлора n-ого порядка функции f(x) в точке х0.
Здесь функция Rn(x), представляющая собой разность между функцией и её многочленом Тейлора, называется n-ым остатком Тейлора.
Примеры.
Формула конечных приращений Лагранжа
f(х) = f(х0) + f ′ (ξ)(х – х0),
где ξ – между х и х0, f(х0) = T 0(x), f ′ (ξ)(х – х0 ) = R0(x).
Это формула Тейлора нулевого порядка с остатком в форме Лагранжа.
Если f(х) дифференцируема в точке х0, то
f(х) = f(х0) + f ′ (х0)(х – х0) + о(х – х0).
Это формула Тейлора первого порядка с остатком в форме Пеано.
cosx = 1 – x2/2 + o(x2).
Это формула Тейлора второго порядка с остатком в форме Пеано.
Слайд 5Формула Тейлора с остатком в форме Лагранжа.
ТЕОРЕМА 1.
Пусть
функция f(x) n+1 раз дифференцируема в Uδ(x0). Тогда для f(x)
справедлива формула Тейлора n-ого порядка в точке х0, причёмгде ξ – между х и х0.
Доказательство.
Пусть, для определенности, x > x0.
Rn(x) = f(x) – Tn(x).
Заметим, что
Rn(x0) = R'n(x0) = R''n (x0) = … = Rn(n)(x0) = 0,
Rn(n+1)(x) = f (n+1)(x) для ∀х∈ Uδ(x0).
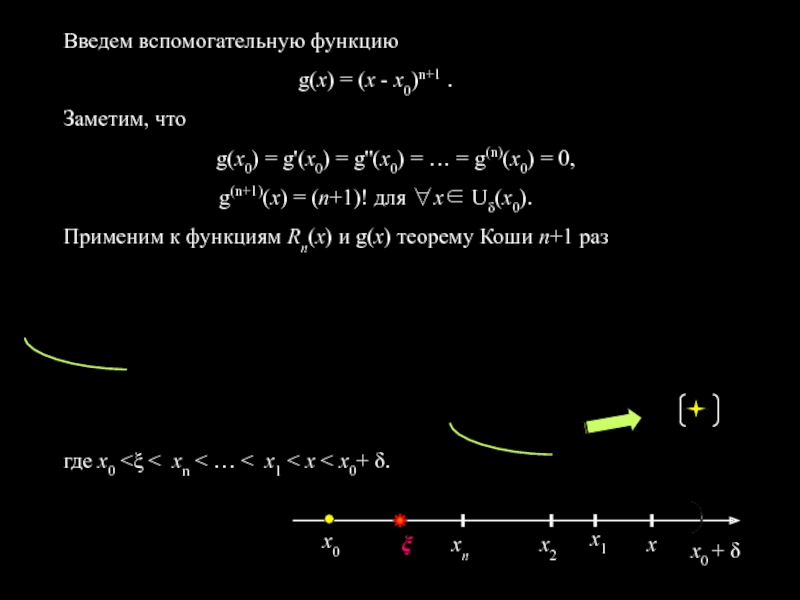
Слайд 6 Введем вспомогательную функцию
g(x) = (x - x0)n+1 .
Заметим, что
g(x0)
= g'(x0) = g''(x0) = … = g(n)(x0) = 0,
g(n+1)(x) = (n+1)! для ∀х∈ Uδ(x0).
Применим к функциям Rn(x) и g(x) теорему Коши n+1 раз
где x0 <ξ < xn < … < x1 < x < x0+ δ.
x0
x
x1
xn
ξ
x0 + δ
x2
Слайд 7Формула Тейлора с остатком в форме Пеано.
ТЕОРЕМА 2.
Пусть функция
f(x) n раз дифференцируема в Uδ(x0)
и f (n)(x) непрерывна
в точке x0. Тогда при х→ x0 функция может быть представлена в виде
Замечание.
Последнюю формулу называют формулой Тейлора с остатком в форме
Пеано или локальной формулой Тейлора.
Слайд 8Доказательство.
Так как f(x) n раз дифференцируема в Uδ(x0), то
для нее справедлива
формула Тейлора с остатком в форме Лагранжа
порядка (n-1):где ξ между х и x0.
f (n)(ξ) → f (n)(x0) при х → x0, т.е. f (n)(ξ) = f (n)(x0) + о(1) при х → x0.
Тогда получим, что
Слайд 9Джузеппе Пеано (1858-1932).
Итальянский математик и логик. Член Туринской Академии
Наук. Окончил Туринский университет. Работал там же.
Пионер и пропагандист символической
логики. Исследовал основные понятия и утверждения анализа (вопросы о возможно более широких условиях существования решений дифференциальных уравнений, понятие производной и другие). Занимался формально-логическим обоснованием математики. Слайд 10Единственность представления функции f(x) в виде многочлена по степеням (х
– х0)
ТЕОРЕМА 3.
Пусть функция f(x) n раз дифференцируема в Uδ(x0)
и f (n)(x) непрерывна в точке x0. Если при х→ x0 функция представима в видето коэффициенты
Слайд 11Доказательство.
Для функции f(x) выполнены условия теоремы 2, тогда
Переходя к пределу
при х→ x0 в левой и правой частях равенства, получим
a0 = f(x0).
Отбросим равные члены и поделим на (x - x0). Переходя к пределу при х→ x0, получим
a1 = f '(x0).
И т.д.
Итак, единственным многочленом наилучшего приближения для функции f(x) при х→ x0 является ее многочлен Тейлора.
Слайд 12Разложение основных элементарных функций по формуле Тейлора.
Если в формуле Тейлора
х0 = 0, то в этом частном случае ее называют
формулой Маклорена. Формула Маклорена с остатком в форме Пеано имеет следующий вид:Или
Получим разложения основных элементарных функций по формуле Маклорена.
Слайд 13 f(x) = ех
f (k)(x) = ех; f (k)(0)
= 1, k = 0, 1, 2, …
f(x) =
shx f (2k)(x)= shx, f (2k +1)(x)= chx;
f (2k)(0) = 0, f (2k+1)(0) =1, k = 0, 1, 2, …
f(x) = chx
f (2k)(x)= chx, f (2k +1)(x)= shx ;
f (2k)(0) = 1, f (2k+1)(0) = 0, k = 0, 1, 2, …
Слайд 14
f(x) = sinx
f (k)(x)= sin(x + kπ/2);
f
(2m)(0) = 0, f (2m+1)(0) = (-1)m, m = 0,
1, 2, …f(x) = cosx
f (k)(x)= cos(x + kπ/2);
f (2m)(0) = (-1)m, f (2m+1)(0) = 0, m = 0, 1, 2, …
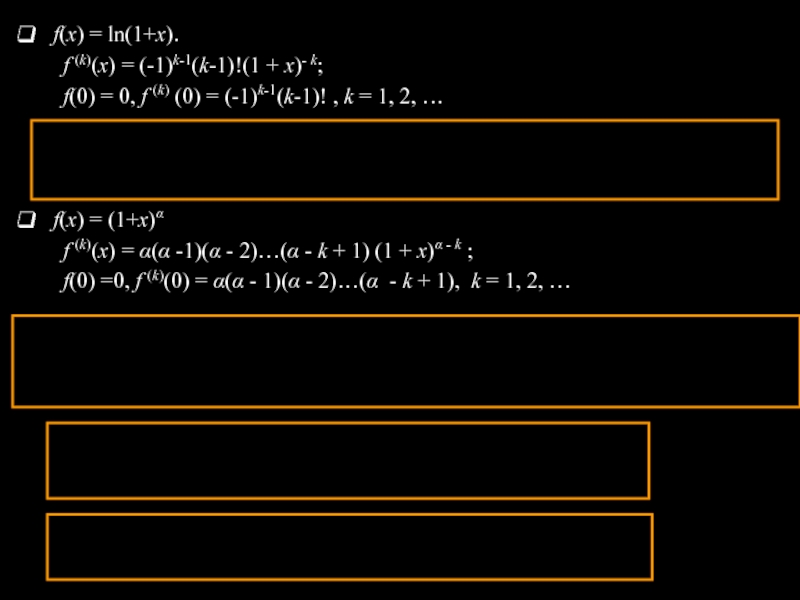
Слайд 15f(x) = ln(1+x).
f (k)(x) = (-1)k-1(k-1)!(1 + x)- k;
f(0) = 0, f (k) (0) = (-1)k-1(k-1)! , k
= 1, 2, … f(x) = (1+x)α
f (k)(x) = α(α -1)(α - 2)…(α - k + 1) (1 + x)α - k ;
f(0) =0, f (k)(0) = α(α - 1)(α - 2)…(α - k + 1), k = 1, 2, …
















![Звук [з], буква З Презентация к план-конспекту занятия по подготовке к обучению](/img/tmb/7/649972/4ac4bf70559e762cea360bf053974418-800x.jpg)

















