Слайд 1Основные понятия фрактальной геометрии и фрактальной физики.
Примерно до
середины прошлого века физика стремилась к идеализации окружающего мира, который
был разнообразен и многолик, один объект этого мира, будучи даже очень похож на другой, все равно от него отличался, и чем глубже мы их изучали, тем больше различий обнаруживалось. Было от чего придти в отчаяние и повеситься. Жаль, что многие этого решительного шага не сделали.
С целью приведения своих заскорузлых, но таких приятных, радующих глаз и удобных для расчета представлений об идеальном физическом объекте наши предки пытались строить модели объектов реального мира из простых геометрических фигур: прямых линий, правильных окружностей, кубов, параллелепипедов, сфер и многогранников. Классическая кристаллография имела дело исключительно с идеализированными формами, в которые пыталась запихнуть прекрасный окружающий мир
Слайд 2 Историческими объектами геометрического анализа служили 5 многогранников Платона,
13 многогранников Архимеда, 4 многогранника Кеплера-Пуансо.
В 1830
г. И. Гессель вывел 32 кристаллографических класса, содержащих элементы симметрии порядка 1,2,3,4,6, описывающие все возможные формы кристаллических тел в виде многогранников.
Оси 5-го порядка категорически запрещены классической кристаллографией, хотя она признает их существование в живой природе. Еще бы ей этого не признавать!
Слайд 3 Традиционные методы геометрии, широко используемые в естественных науках,
в том числе в материаловедении и механике деформируемых тел, основаны
на приближенной аппроксимации структуры исследуемого объекта геометрическими фигурами, например линиями, отрезками, плоскостями, многоугольниками, многогранниками, сферами.
При этом внутренняя структура исследуемого объекта, как правило, игнорируется, а процессы образования структур и их взаимодействие между собой и с внешней средой характеризуются усредненными, интегральными параметрами.
Это приводит к утрате значительной части информации о свойствах и поведении исследуемых систем, которые, в сущности, заменяются более или менее адекватными моделями, причем скорее менее, чем более (чем больше женщину мы меньше, тем меньше больше она нам).
Слайд 4 С помощью таких классических подходов описать реальный мир
невозможно примерно в 90% случаев.
Дельта
Амазонки
Дельта
Дуная
Дельта
Невы
Слайд 5 В 1972 г. бельгийский математик Бенуа Мандельброт (Benoit
Mandelbrot) ввел понятие фрактала и фрактальной геометрии для описания реальных
объектов и математических абстракций. На первых порах с абстракциями получалось гораздо лучше.
Название фрактал Мандельброт произвел от латинского "fractus", что означает дробный, ломаный, нерегулярный, фрагментарный, рекурсивный, создающий фрагменты неправильной формы, и определил как структуру, состоящую из частей, которые в каком-либо смысле подобны целой структуре.
Определение это оказалось чрезвычайно широким, поскольку под него попадают практически все объекты реального мира.
Слайд 6 В другой, тоже авторской трактовке, фрактал - это
самоподобная структура, чье изображение не зависит от масштаба.
Это рекурсивная модель, каждая часть которой повторяет в своем развитии развитие всей модели в целом.
Фрактал, инвариантный при обычном геометрическом преобразовании, называется самоподобным.
Основной термин фрактал подразумевает неупорядоченность и относится к структурам ярко выраженной иррегулярности, тогда как определение масштабно-инвариантный означает наличие некоторого порядка, хотя в окружающем мире нет ничего строго однородного или строго масштабно-инвариантного.
(Рекурсивность – термин, обозначающий повторяющийся характер любого феномена, устанавливающий отношения различия с тем, что повторяется).
Слайд 7 Согласно классическому определению Мандельброта некоторый объект называется самоподобным,
если сам объект, взятый целиком, можно разделить на "части", каждая
из которых получается из целого посредством преобразования подобия, то есть редукции или линейного сжатия.
Слайд 8 Таким образом Мандельброт постулировал, что фрактальная структура обладает
иерархичностью и масштабной инвариантностью (скейлингом), а одним из важнейших свойств
фрактала является свойство самоподобия, т.е. их вид не меняется в любом пространственном масштабе.
Сие означает сохранение принципа подобия при различных уровнях рассмотрения структуры - в идеале от применения атомного силового микроскопа до наблюдений из кабины космического корабля (разумеется, российского производства).
Слайд 9 Если под фрактальной структурой понимать любую сложно организованную
на принципах самоподобия иерархическую систему, то почти любую твердотельную структуру
можно рассматривать как фрактальную.
Поскольку представлениям об иерархии придается одно из основополагающих значений в системных исследованиях, то необходимо охарактеризовать его исходные контуры, дать его рабочее определение.
Под иерархией, под иерархическими системами понимают системы, которые состоят из ансамбля последовательно "вложенных" одна в другую взаимодействующих и взаимообусловливающих подсистем.
Слайд 10 Такие системы характеризуются наличием взаимосвязанных и взаимозависимых уровней
их внутреннего строения и детерминации.
Каждая подсистема, каждый
из уровней представлен своими структурными единицами и процессами, на каждом из них действуют специфические закономерности и решаются свои задачи.
Основу представлений об иерархии составляют характер, закономерности взаимоотношений между уровнями, между "вложенными" друг в друга подсистемами.
Понятие иерархии включает в себя представления о субординации, о взаимном соподчинении подсистем и уровней.
Структуры и функции процессов на вышележащих уровнях надстраиваются над структурами и функциями на нижележащих уровнях, чем и определяется характер их иерархических отношений.
Слайд 11 Иерархия реальных систем включает в себя и жесткие.
однозначно определяемые зависимости, и лабильные, подвижные взаимоотношения, характеризующиеся наличием независимости
в отношениях между параметрами подсистем и элементов, наличием внутренней активности и элементов самоорганизации на каждом из уровней.
Особо наглядно высшие формы иерархии проявляются при рассмотрении особенностей внутренней организации живых систем.
Весьма существенно, что в иерархических отношениях здесь ведущее значение приобретают информационные взаимодействия.
При анализе природы иерархии необходимо иметь в виду ее "назначение".
Слайд 12 Идея иерархии направлена на обеспечение устойчивого функционирования как
всей системы в целом, так и процессов на каждом из
ее структурных уровней.
Устойчивое функционирование систем в целом поддерживает и опирается на "оптимальное" функционирование подсистем и элементов, и обратно, сбои на нижележащих уровнях приводят к ограничению эффективности деятельности систем в целом и даже к их разрушению.
При этом в случае сложных систем необходимо учитывать их открытость, наличие взаимодействий и обмена веществ, энергией и информацией с окружением и представления о целях как характеристиках направленных изменений и систем в целом, и их подсистем.
Познание иерархически организованных систем закрепляется в системах соответствующих понятий.
Слайд 13 Подобие фрактальных структур различных объектов, таких, например, как
турбулентность в жидкости и спиральная структура галактик говорит о том,
что чем выше мерность объекта Природы или чем ближе он к иерархическим началам, тем проще он устроен.
Вполне возможно, что фрактальный реальный объект является одно-, двух- или трехмерным отражением некой многомерной структуры в частности и многомерной структуры Вселенной в общем.
Фрактальная размерность, в некотором несогласии с Мандельбротом, может полностью соответствовать эвклидовой размерности, примером чего является лоренценово множество.
Б. Мандельброт создал неэвклидову геометрию негладких, шероховатых, зазубренных, изъеденных ходами, порами, трещинами и отверстиями извилистых и тому подобных объектов, своего рода математических парий, по молчаливому уговору ранее исключавшихся из рассмотрения (в пользу усредненных, сглаженных, отполированных объектов), а именно они составляют подавляющее большинство объектов природы.
Слайд 14 Наиболее осмысленное и емкое определение фрактала дано П.В.
Короленко: "Фракталами называются геометрические объекты: линии, поверхности, пространственные тела, имеющие
сильно изрезанную форму и обладающие свойством самоподобия.
Самоподобие как основная характеристика фрактала означает, что он более или менее единообразно устроен в широком диапазоне масштабов.
При увеличении маленькие фрагменты фрактала получаются очень похожими на большие".
Это предопределяет масштабную инвариантность (скейлинг) основных геометрических особенностей фрактального объекта, их неизменность при изменении масштаба.
Слайд 15 Вырезав небольшую часть из структуры, имеющей свойства фрактальности,
мы можем рассмотреть ее в некотором увеличении и обнаружить, что
она подобна всей структуре в целом.
Вырезав еще более мелкую часть из уже вырезанной части и увеличив ее, мы опять же с немалым удивлением обнаружим, что и она подобна первоначальной структуре.
Если рассматривать идеальную фрактальную структуру, такую операцию мы можем проделывать до бесконечности, и даже самые микроскопические частички будут подобны структуре в целом. Поскольку теоретики, а особенно математики, никогда не слышали, а уж тем более не применяли на практике такие скучные и прозаические вещи, как предел делимости материи, элементарная частица и прочее, то такая точка зрения имеет право на жизнь в человеческом мозгу.
Слайд 16
Природные же и техногенные фракталы имеют четко ограниченный
интервал масштабов, в котором сохраняется принцип фрактальности и в котором
они проявляют свою фрактальную природу.
В реальности любой фрактал имеет некоторый минимальный и максимальный масштаб длины, при меньших или больших значениях этой длины самоподобие пропадает или нарушается.
Слайд 17 Глобальная размерность оценивает рост числа объектов бесконечно малого
диаметра, необходимых для того, чтобы покрыть данную форму и изменяется
от размерности гладкого объекта до размерности пространства.
Её также называют размерностью Хаусдорфа - Безиковича.
Пусть мы имеем дело с круговым или сферическим объектом массой М и радиусом R. Справедливо соотношение М ~ RЕ, где Е - размерность (число координат) пространства.
Для фрактальных объектов справедливо соотношение М ~ RD, где D - фрактальная размерность, не совпадающая с пространственной размерностью.
Отсюда можно сделать вывод, что фрактальная геометрия описывает объекты с дробными размерностями.
Слайд 18 Для наглядности построим один из фрактальных геометрических объектов
(кривая Коха) и найдем его размерность. Еще в 1904 году,
шведский математик Нильс Фабиан Хельге фон Кох (Niels Fabian Helge von Koch), (1870-1924), сделал попытку описать кривую, для которой несмотря на то, что она почти везде непрерывна, не определена производная и она не дифференцируема.
Фон Кох имел несчастье заполучить странноватое для нашего слуха имя Хельге, переведенное высокообразованными гуманитариями как Ольга, что позволяет некоторым нашим продвинутым ученым искренне считать его женщиной.
Они не правы, т.к. роскошная борода и усы, отчетливо различимые на фотографии Коха, позволяют, по крайней мере по вторичным половым признакам, отнести его к мужчинам.
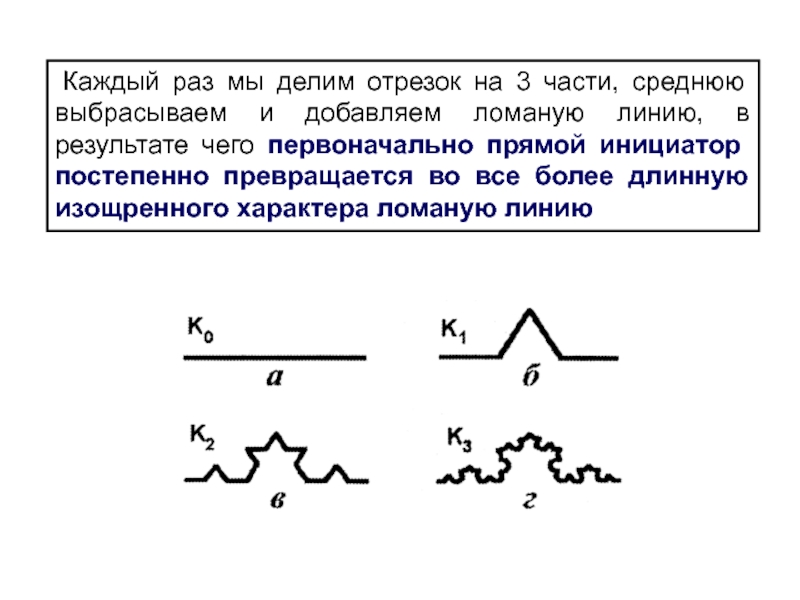
Слайд 19 Возьмем отрезок прямой единичной длины К0, назовем его
инициатором и разделим на три равные части.
Теперь
среднюю часть выкинем и заменим ее двумя такими же отрезками, равными 1/3 от первоначального и соединенными друг с другом и оставшимися отрезками, получив таким образом второе приближение - ломаную линию, составленную из четырех отрезков равной длины К1 и назовем ее генератором.
Далее каждый прямой отрезок получившейся ломаной линии будем преобразовывать согласно этому алгоритму.
Будем повторять эту операцию до бесконечности, поскольку в математике нет понятия предела делимости материи.
Слайд 20 Каждый раз мы делим отрезок на 3 части, среднюю
выбрасываем и добавляем ломаную линию, в результате чего первоначально прямой
инициатор постепенно превращается во все более длинную изощренного характера ломаную линию
Слайд 21 Поскольку на каждом шаге каждый отрезок разбивался на
три части (а мог бы и на четыре и более),
то в итоге получаем фигуру, названную Мандельбротом триадный терагон (от греческого слова терос - чудовище, странное создание) Коха, длина стороны которого ε при каждом шаге уменьшается, стремясь в пределе к бесконечно малой величине, но число таких сторон адекватно увеличивается, стремясь к бесконечности.
При этом при каждом шаге длина кривой Коха L(ε) увеличивается на треть и при бесконечном числе шагов длина линии бесконечна.
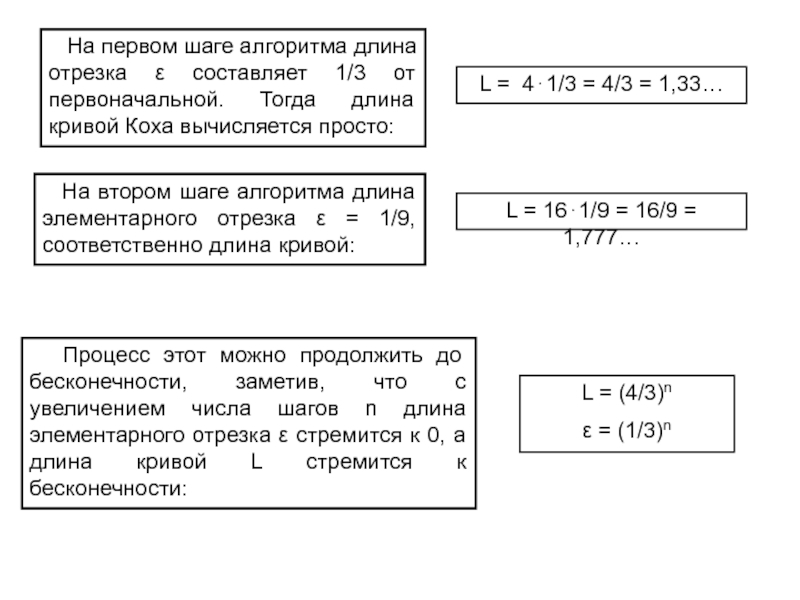
Слайд 22L = 16⋅1/9 = 16/9 = 1,777…
L = 4⋅1/3 =
4/3 = 1,33…
На первом шаге алгоритма длина
отрезка ε составляет 1/3 от первоначальной. Тогда длина кривой Коха вычисляется просто:
На втором шаге алгоритма длина элементарного отрезка ε = 1/9, соответственно длина кривой:
Процесс этот можно продолжить до бесконечности, заметив, что с увеличением числа шагов n длина элементарного отрезка ε стремится к 0, а длина кривой L стремится к бесконечности:
L = (4/3)n
ε = (1/3)n
Слайд 23 Из этих выражений получаем: n = (1/lnЗ)⋅ln(1/ε). Подставляя
n получим:
L = exp[n⋅ln(4/3)] = exp[(ln(4/3)/ln3]⋅ln(l/ε)
Обозначив
D = ln4/ln3, получаем:
Из последнего соотношения видно, что постоянным показателем остается только величина D, поскольку она не зависит от масштаба измерения и является характеристикой данной линии "кривая Коха". Она называется фрактальной размерностью.
Слайд 24 С геометрической точки зрения фрактальная размерность является показателем
того, насколько плотно эта линия заполняет плоскость или пространство.
Аналогичным образом можно рассчитать фрактальную размерность других регулярных фракталов, например, плоского регулярного фрактала - салфетки Серпинского и множества других, измысленных математиками.
Получается, что фрактальная размерность такой линии больше, чем у прямой линии, но меньше, чем у плоскости.
На самом деле мы имеем дело с особым физическим (или математическим) объектом, относящимся к классу множеств.
В зависимости от того, как мы его измеряем, он несколько меняет свои параметры, а, возможно, и свойства.
Это уже не линия, но еще и не полноценная плоскость.
Слайд 25 Кривую Коха можно растянуть в прямую линию, поэтому
ее топологическая размерность равна единице.
Фрактальная размерность ее,
равная 1,2618.. больше топологической, что и говорит о том, что кривая является структурой, отличной от линии, но еще не ставшей плоскостью.
Идеально гладкий лист бумаги есть символ плоскости.
Хорошо помятый лист бумаги в принципе представляет собой фрактал, площадь которого зависит от того, как мы его измеряем, хотя до акта помятости никаких сомнений не возникало.
Перевод объекта в иные рамки изменил его свойства. Интересный вопрос о фрактальной размерности тонкой мятой вуали, изготовленной из очень тонких нитей.
Слайд 26 Другим математическим фракталом, имеющим аналоги как в нанотехнологии,
так и в космогонии, является канторова пыль. Инициатором является единичный
отрезок прямой линии.
Первый этап построения состоит в разделении интервала на три части и удаления открытой средней части. С глаз долой, из сердца вон.
Затем удаляются средние трети у каждого из N=2 оставшихся отрезков. И так до бесконечности.
Образовавшееся множество остатков С определяется как двоичное, поскольку N=2, и называется канторовым дисконтинуумом, но Мандельброт предложил его называть канторовой пылью.
Множество, полученное в результате этих несложных манипуляций, самоподобно, а его размерность определится, как:
Слайд 27 Изменяя алгоритм построения (можно делить на 5 частей
и удалять четные и т.п.) можно получать и другие значения
фрактальной размерности, лежащие в интервале 0 - 1.
С топологической же точки зрения все канторовы множества имеют размерность 0, так как по определению, любая точка канторова множества отделена от любой другой, причем для ее отделения ничего не надо удалять. В пределе число этих точек стремится к бесконечности, но в зависимости от генератора это будут разные бесконечности, отличающиеся своей фрактальной размерностью.
Каждая из этих бесконечностей будет характеризоваться своей фрактальной размерностью. Мы впервые получаем мощный инструмент для анализа разных бесконечностей с помощью фрактальной размерности.
Слайд 28 Интервал самоподобия различных природных объектов может содержать масштабы
от долей микрометра при рассмотрении структуры пористых горных пород и
сплавов металлов до десятков километров при рассмотрении рельефа местности и формы облаков.
В качестве примеров естественных (природных) фракталов можно привести деревья, облака, реку и разветвленную сеть ее притоков, систему кровообращения человека, "морозные" узоры на стекле и т.д.
Слайд 29 Если совершенно разные, но схожие между собой объекты
характеризуются одной фрактальной размерностью, то мы вправе предположить, что они
обладают и сходным свойствами в каком-то ограниченном масштабе.
Поэтому, изучая свойства доступного фрактального объекта, мы можем прогнозировать свойства другого фрактального объекта, нам не доступного, но имеющего такую же фрактальную размерность - например, звездную систему.
Самоподобие предполагает, что копирование и масштабирование некоторого "эталонного" образа позволяет природе легко создавать сложную многомасштабную структуру.
Знать бы еще, как это делается, и можно было бы спокойно спать.
Слайд 30 Математические фракталы обладают удивительной и неповторимой красотой. Сейчас
известно громадное количество алгоритмов их построения и использование самых разных
инициаторов и генераторов.
Появление мощных компьютеров дало своеобразный импульс к псевдохудожественному творчеству в области фрактальной геометрии. В Интернете можно найти целые галереи различных математических фракталов, которые, надо честно признать, просто завораживают своей удивительной, странной и неповторимой красотой.
Долгое рассматривание таких картинок благотворно влияет на человеческую психику – почти, как рыбки в аквариуме.
Но при этом надо все время помнить бессмертные слова Козьмы Пруткова – "Бросая камешки в воду, наблюдай за кругами, ими образуемыми. Иначе занятие это будет пустою забавою«.
Слайд 31"Дракон Пеано".
"Губка Менгера"
Салфетка Серпинского
Множество Мандельброта
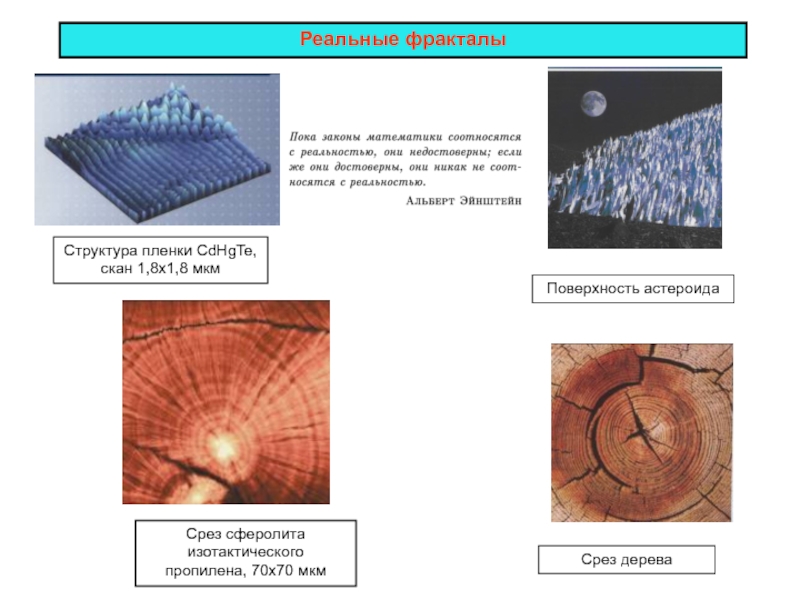
Слайд 36Реальные фракталы
Структура пленки CdHgTe,
скан 1,8х1,8 мкм
Срез сферолита изотактического
пропилена, 70х70 мкм
Срез
дерева
Поверхность астероида
Слайд 37Среднеазиатская пустыня
Коллаген на Та подложке,
скан 50х50 нм
Очертания ледника в Бутане
Береговая
линия Гренландии
Слайд 38 Фрактальный агрегат каждого вещества формируется при определенных физических
условиях, которые до конца не поняты.
Тем не
менее, то, что уже известно, дает возможность использовать законы образования фрактальных агрегатов для создания материалов с необычными физическими свойствами.
Так, можно создавать материалы, способные поглощать электромагнитное излучение в достаточно широком диапазоне длин волн, новые красители, жидкокристаллические системы, наноструктуры, твердые вещества с пористостью до 99% и новые технологии борьбы с накипью в паровых котлах и энергетических установках, и конечно же - новые образцы вооружения.
Слайд 39 Реальные физические структуры, как природные, так и техногенные,
могут являться (а чаще всего и являются) суммой или разностью
множеств с различной фрактальной и топологической размерностью.
Причем ни одно из этих множеств нельзя исключить из рассмотрения без потери информации об объекте, даже если они пренебрежимо малы как во фрактальном, так и топологическом смысле.
Такую совокупность множеств принято называть неоднородным фракталом.
Слайд 40 Работа Мандельброта не являлась причудой впавшего в маразм
теоретика, а была связана с реальной, насущной задачей, получившей название
"Определение длины береговой линии". На самом деле проблема была в том, что длина государственной границы между двумя государствами оказывается разной для одного государства и для другого.
Для Испании - Португалии и Бельгии - Нидерландов эта разница, согласно официальным сведениям, опубликованных в справочниках, составляет до 20 %, что может привести даже к локальному конфликту, несмотря на то, что эти государства полностью привержены изумительным общечеловеческим западным демократическим ценностям, с энтузиазмом борются за права человека, обезьяны и клопа домашнего обыкновенного и даже говорят по обе стороны границы практически на одних и тех же языках.
А вот длина общей границы разная - какой пассаж!
Слайд 41 Для начала рассмотрим простую задачу об определении длины
береговой границы озера. Если радиус озера представить величиной R, то
площадь поверхности этого озера S = πR2. Проведем измерение периметра этого озера.
Интуитивно кажется ясным, что длина береговой линии озера L не должна зависеть от того, какой линейкой мы ее измеряем.
Однако, как ни странно, это совершенно не так.
Возьмем 100-метровую линейку и проведем измерение таким образом, чтобы концы линейки были на границе раздела вода-суша. Полная длина ломаной линии - это периметр озера.
Затем возьмем 10 метровую линейку и с ее помощью измерим периметр озера. В этом случае он будет большим и будет лежать внутри предыдущего.
Если же измерить периметр озера 1 метровой линейкой, то он увеличится еще больше, и так далее.
Слайд 42С каждым увеличением точности метрологического инструмента величина казалось бы неизменной
береговой линии все время увеличивается. Таким образом получается, что периметр
озера зависит от масштаба измерения.
По мере того как длина линейки (масштаб измерения) уменьшается, длина ломаной линии все возрастает как L = I(R / I)D, где I -величина используемого масштаба.
Параметр D является фрактальной размерностью береговой линии.
Слайд 43 Береговая линия озера является множеством, занимающим промежуточное положение
между обычной линией (D = 1) и поверхностью (D =
2), причем величина 1 < D < 2 тем больше, чем более изрезанным и неоднородным является берег.
Совершенно аналогичная ситуация при определении государственной границы. Разные страны измеряли ее разным масштабом измерения.
Слайд 44Отсюда следует вывод, что все границы между государствами, береговые линии,
границы облаков и людских толп, вопящих на площадях и майданах
- суть фрактальные объекты.
С определенными, очень грубыми допущениями, их можно аппроксимировать кривой Коха, но лучше этого не делать, а честно преодолевая немыслимые трудности заняться измерением фрактальной размерности реальных физических объектов.
Кривая Коха все-таки представляет собой в действительности не модель береговой линии или границы, а их математический эскиз.
Слайд 45 Еще более интересным является анализ реальных объектов, которые
можно сопоставить с канторовой пылью.
С одним из
них каждый из нас внутренне знаком от момента рождения до момента наступления летального исхода.
Речь идет о системе кровообращения, которая состоит из двух подсистем - артериальной и венозной.
Первая из них получает кислород от легких и доносит его и другие необходимые для жизнедеятельности клеток ингредиенты до каждой клетки утомленного организма, а вторая удаляет из них продукты метаболизма.
Слайд 46Это значит, что в принципе является абсолютно необходимым, чтобы и
артерия, и вена были расположены бесконечно близко от любой клетки
или точки тела, — исключая, разумеется, точки, находящиеся внутри артерий или вен.
Мандельброт сформулировал это еще более странно: каждая точка ткани, не относящей системе кровообращения, должна лежать на границе между двумя кровеносными системами.
При этом существует еще конструкторское ограничение, заключающееся в том, что кровь нужно экономить, особенно если в ней большой процент алкоголя.
Слайд 47 Отсюда полный объем всех артерий и вен должен
составлять лишь малый процент от объема тела, оставляя основную часть
пространства тканям.
В человеческом организме вся кровь объемом около 5 литров в течение одной минуты полностью прокачивается сердцем через сеть капилляров общей длиной порядка 100 тысяч километров.
С точки зрения классической физики и евклидовой геометрии, эти требования невыполнимы, аномальны и анормальны.
Искомая фигура должна быть топологически двумерной, так как она образует границу, общую для двух топологически трехмерных фигур, причем требуется, чтобы ее объем являлся одновременно не только пренебрежимо малым по сравнению с объемами фигур, которые она ограничивает, но и гораздо больше этих объемов. Однако, что недоступно жалкому гуманитарию, то доступно физику.
Слайд 48 Одно из достоинств фрактального подхода к анатомии заключается
в том, что вышеуказанные требования прекрасно сочетаются друг с другом.
Вены и артерии являются стандартными трехмерными областями, поскольку в них должны целиком умещаться сферы малого радиуса (кровяные шарики).
С другой стороны, сосуды занимают очень небольшую долю от общего объема тела. Ткань - иное дело; в ней нет ни одного участка, сколь угодно малого, который не был бы пересечен и артерией, и веной.
Ткань представляет собой фрактальную поверхность: ее топологическая размерность 3, а фрактальная размерность 2. В таком виде вышеприведенные критерии теряют всю свою экстравагантность, а система представляет собой одну из разновидностей канторова множества.
Слайд 49 С помощью фрактальной физики легко объясним и такой
парадокс, как эффект пылающего неба, заключающийся в том, что в
случае бесконечной Вселенной в ней бесконечное количество звезд, и небо ночью должно просто пылать.
Поскольку количество излучаемого звездой света прямо пропорционально площади ее поверхности, количество света, достигающее наблюдателя, находящегося от звезды на расстоянии R, должно быть пропорционально 1/R2, но площадь видимой поверхности звезды также пропорциональна 1/R2. Таким образом, отношение количества света к видимому сферическому углу не зависит от R.
Кроме того, если распределение звезд во Вселенной равномерно, то практически любое направление взгляда рано или поздно встретит какую-нибудь звезду.
Следовательно, небо должно быть освещено звездным светом равномерно и выглядеть просто пылающим - днем и ночью.
Слайд 50 Если же допустить, что Вселенная фрактальна и что
ее размерность D < 2, то парадокс разрешается сам собой.
В этом случае проекция Вселенной на небесный свод является фрактальным множеством той же размерности D, т.е. множеством нулевой площади.
Даже если звезды имеют ненулевой радиус, большая часть направлений уходит в бесконечность, не встречая на своем пути ни одной звезды. Если смотреть вдоль этих направлений, то мы увидим только черноту ночного неба.
Если за интервалом, в котором D < 3, следует интервал, в котором D = 3, то фон неба будет не строго черным, но чрезвычайно слабо освещенным. Это простое рассуждение является еще одним кирпичиком в здание теории фрактальной Вселенной, причем неважно, конечной или бесконечной.
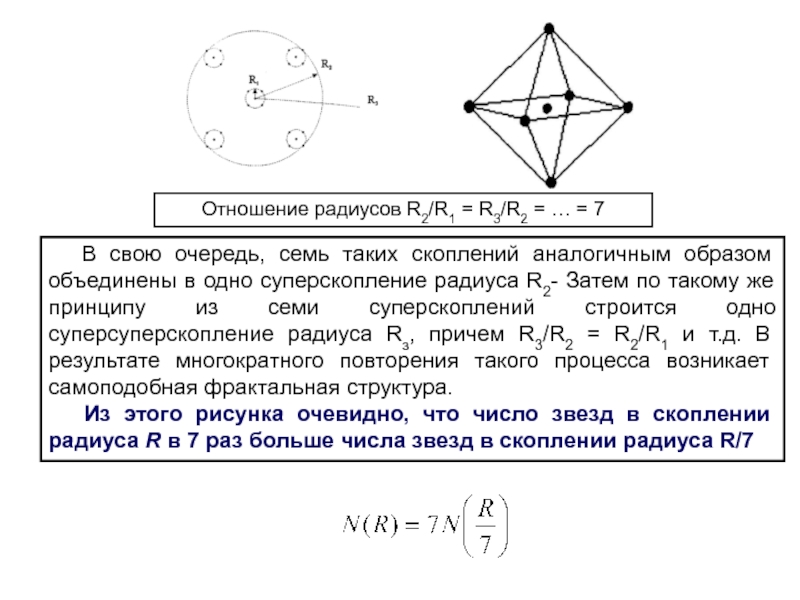
Слайд 51 Представим себе сферу очень большого радиуса R (космических
масштабов), внутри которой находится очень большое число звезд N >>
1.
Ясно, что число N должно расти с увеличением радиуса сферы. Нас как раз и будет интересовать эта зависимость N(R).
Если бы звезды, галактики, скопления галактик были бы распределены во Вселенной равномерно с некоторой постоянной плотностью, то число звезд в сфере радиуса R было бы пропорционально объему этой сферы, т.е.
N ∝ R3
Астрономические наблюдения, однако, показывают, что:
N ∝ RD, где D ≈ 1,23,
Таким образом хаусдорфова размерность Вселенной гораздо ближе к 1, чем к 3.
Это означает, что наша Вселенная почти одномерна!
Слайд 52 Как можно это понять качественно? Для этого обратимся
к примеру Вселенной Фурнье.
Она была предложена в
1907 г. американским неудавшимся физиком, но удавшимся писателем фантастом Фурнье. Фрагмент ее структуры показан далее на рисунке.
Каждая точка на этом рисунке представляет собой одну галактику. Они объединены в скопления радиуса R1 по 7 галактик в каждом скоплении.
На рисунке видны только пять из них: недостающие две расположены симметрично над и под плоскостью рисунка, на прямой, проходящей через центр скопления.
Слайд 53 В свою очередь, семь таких скоплений аналогичным образом
объединены в одно суперскопление радиуса R2- Затем по такому же
принципу из семи суперскоплений строится одно суперсуперcкопление радиуса Rз, причем R3/R2 = R2/R1 и т.д. В результате многократного повторения такого процесса возникает самоподобная фрактальная структура.
Из этого рисунка очевидно, что число звезд в скоплении радиуса R в 7 раз больше числа звезд в скоплении радиуса R/7
Отношение радиусов R2/R1 = R3/R2 = … = 7
Слайд 54 Полагая N ∝ RD, получим D = 1.
Таким образом, вселенная Фурнье – одномерна!!!
Число 7, проникшее в эту схему, не играет принципиальной роли. На его месте могло бы быть любое другое число.
Ясно также, что, варьируя соотношение между размерами скопления и числом элементов в них, можно построить фрактальные модели Вселенной с другими близкими к 1 размерностями D.
Заметим также, что вселенная Фурнье - точный фрактал, каковым, конечно, наша Вселенная не является.
Как и какие закономерности приводят к фрактальной структуре Вселенной, пока еще не известно.
Слайд 55 Упомянем лишь в этой связи так называемые кольца
Сатурна, которые имеют очень рыхлую и неоднородную структуру со щелями
разных размеров, в которых нет астероидов, от самой большой - так называемое сечение Кассини, до самых маленьких.
Предположительно, что структура колец Сатурна - фрактальна. Если это так, то это было бы ярким подтверждением того, что гравитация способна создавать фрактальные структуры в распределении материи во Вселенной.




















![фрактальная геометрия и физика Из этих выражений получаем: n = (1/lnЗ)⋅ln(1/ε). Подставляя n получим: Из этих выражений получаем: n = (1/lnЗ)⋅ln(1/ε). Подставляя n получим: L = exp[n⋅ln(4/3)] = exp[(ln(4/3)/ln3]⋅ln(l/ε)](/img/thumbs/0a5cde8103ff1f8451884a010a10c7e9-800x.jpg)