Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ФУНКЦИОНАЛЬНО-СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ А.В. Грачев Москва -
Содержание
- 1. ФУНКЦИОНАЛЬНО-СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ А.В. Грачев Москва -
- 2. СодержаниеВведение1. Место функционально символьных вычислений с использованием
- 3. Слайд 3
- 4. 123.13.23.4.Числовой метод ( N)Символьно-числовой ( SN)числовой результат
- 5. ----1. ОБЩАЯ ХАРАКТЕРИСТИКА ФУНКЦИОНАЛЬНО_СИМВОЛЬНЫХ ВЫЧИСЛЕНИЙ С ИСПОЛЬЗОВАНИЕМ
- 6. 1.1. Символьный вывод результата1.2. Символьный вывод с
- 7. 3. СОЗДАНИЕ ФУНКЦИИ ПОЛЬЗОВАТЕЛЯ и ПРОВЕРКА ЕЕ
- 8. 3. СОЗДАНИЕ ФУНКЦИИ ПОЛЬЗОВАТЕЛЯ и ПРОВЕРКА ЕЕ
- 9. 4. Точечные числовые вычисления с использованием функционально-символьной
- 10. Проверка правильности ввода функции с использованием simplify
- 11. Слайд 11
- 12. 7. РАСШИРЕНИЕ ВЫРАЖЕНИЯ . РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ
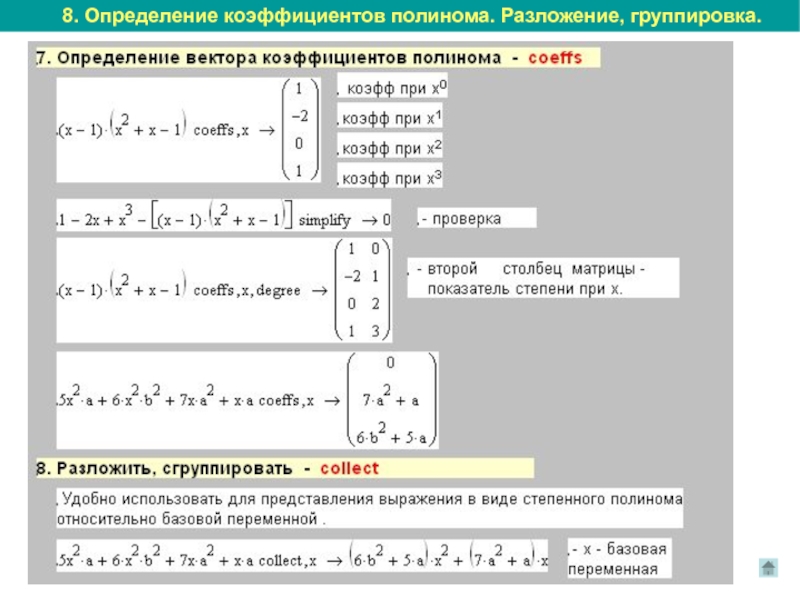
- 13. 8. Определение коэффициентов полинома. Разложение, группировка.
- 14. Слайд 14
- 15. 10. МОДИФИКАЦИЯ – уточнение условий вычисления
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. ПРИМЕРЫ ВЫПОЛНЕНИЯ СИМВОЛЬНЫХ ВЫЧИСЛЕНИЙ И СИМВОЛЬНОГО АНАЛИЗА12.1.
- 20. Слайд 20
- 21. Слайд 21
- 22. 12.3. ЛИНЕЙНАЯ ПЛОТНОСТЬ СЛОЯ, ПОСТУПАЮЩЕГО В ЧЕСАЛЬНУЮ МАШИНУ
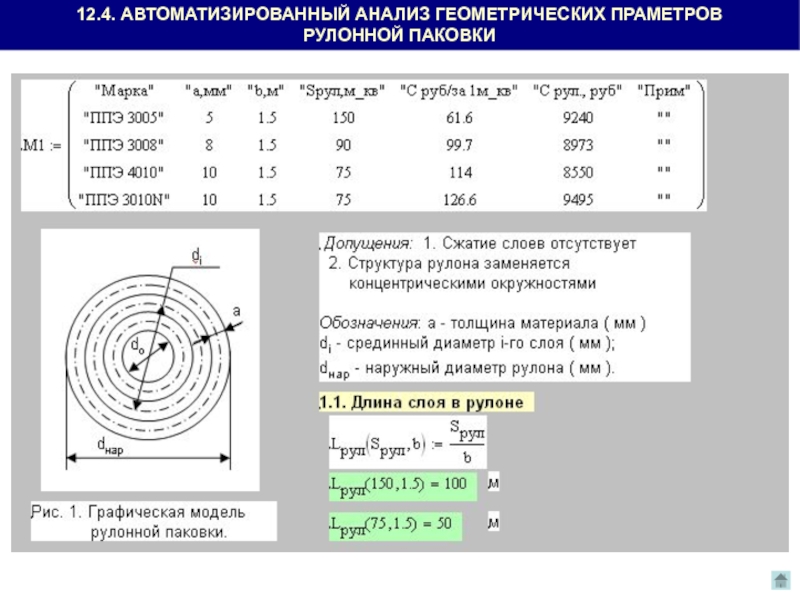
- 23. 12.4. АВТОМАТИЗИРОВАННЫЙ АНАЛИЗ ГЕОМЕТРИЧЕСКИХ ПРАМЕТРОВ РУЛОННОЙ ПАКОВКИ
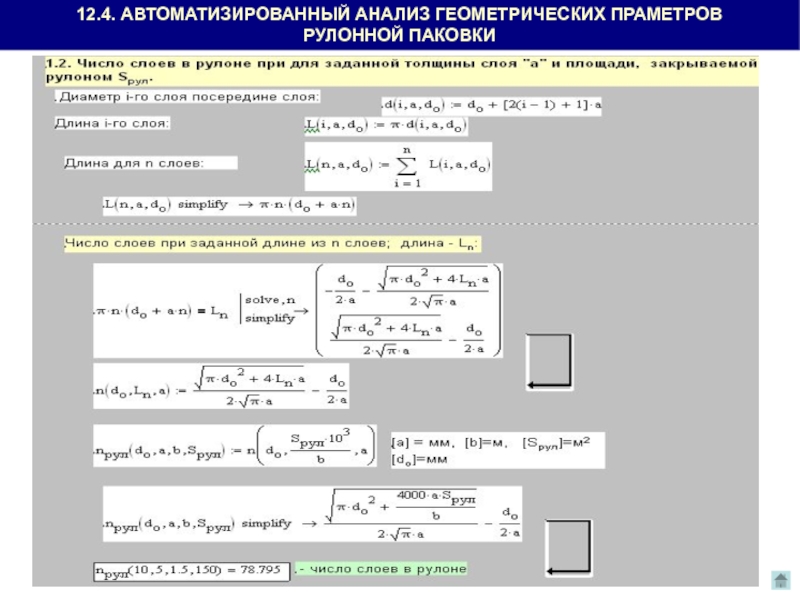
- 24. 12.4. АВТОМАТИЗИРОВАННЫЙ АНАЛИЗ ГЕОМЕТРИЧЕСКИХ ПРАМЕТРОВ РУЛОННОЙ ПАКОВКИ
- 25. 12.4. АВТОМАТИЗИРОВАННЫЙ АНАЛИЗ ГЕОМЕТРИЧЕСКИХ ПРАМЕТРОВ РУЛОННОЙ ПАКОВКИ
- 26. Слайд 26
- 27. Слайд 27
- 28. 14. АНАЛИЗ ФУНКЦИОНАЛЬНОЙ МОДЕЛИ В ВИДЕ ПОЛИНОМА
- 29. 14. АНАЛИЗ ФУНКЦИОНАЛЬНОЙ МОДЕЛИ В ВИДЕ ПОЛИНОМА
- 30. Дальнейшее исследование направлено на проверку
- 31. 15. ИНДИВИДУАЛЬНОЕ ЗАДАНИЕНабрать и отладить листинг 1
- 32. 16. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- 33. 16. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- 34. 16. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- 35. ПРИЛОЖЕНИЕ
- 36. Получение модели в виде полинома второго
- 37. Получение модели в виде полинома второго порядка на основе разложения функции в ряд Тейлораbob2b11b1b12b11
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ФУНКЦИОНАЛЬНО-СИМВОЛЬНЫЕ
ВЫЧИСЛЕНИЯ
А.В. Грачев
Москва - 2011
Версия_2_для_гр_9
31.10.11
Введение в проектирование систем
автоматизированного
технологического анализа
Слайд 2Содержание
Введение
1. Место функционально символьных вычислений с использованием символьного
процессора в общей системе методов вычислений в MathCAD
2. Панель символьных
вычислений3. Создание функции пользователя и проверка правильности ее ввода
4. Точный числовой расчет с использованием функции
5. Упрощение символьных выражений
6. Символьная подстановка
7. Расширение выражения. Разложение его на множители
8. Определение коэффициентов полинома
9. Разложение функции в ряд Тейлора
10. Модификация
11. Символьное решение уравнений
12. Примеры применения
12. 2. Вывод формулы для расчета объема ровничной паковки
14. Анализ модели в виде полинома 2-го порядка
15. Индивидуальное задание
12. 1. Деформация нити
13. Анализ на чувствительность
Приложение. Переход от функции к полиному второго порядка на основе разложения в ряд Тейлора.
12. 3. Определение линейной плотности входного потока
16. Контрольные вопросы и задачи
12. 4. Автоматизированный анализ геометрических параметров рулонной паковки.
Слайд 3 Рассмотренный ранее
символьно-числовой метод расчета в MathCAD позволял проводить числовые технологические расчеты
в скалярной и векторно-матричной формах, а также создавать системы автоматизированного технологического расчета.Однако, метод требовал задания математических моделей в явной форме, а результат всегда имел числовую форму. Таким образом, предварительный вывод моделей, по которым осуществлялся расчет, реализовывался экспертом. Это приводит нас к мысли о том, что дальнейшее развитие вычислительной среды должно обеспечивать вывод и преобразование самих символьных выражений, облегчая эксперту фазу вывода и исследования символьных математических моделей. Такая возможность реализуется в MathCAD за счет введения в него символьного процессора, позволяющий осуществлять буквенные ( символьные) преобразования и выводом результата в символьной форме. Это позволяет автоматизировать часть символьных технологических вычислений, которые ранее выполнялись только экспертом, повысить их доступность и надежность, более широко ставить вычислительные технологические задачи.
Появление возможности символьных вычислений позволяет вместо числового результата получать результат символьный, а вести символьное исследование модели. При этом всегда сохраняется возможность перехода к числовому результату. Этот новый уровень вычислений существенно расширяет информацию, получаемую об объекте. Поэтому можно говорить об автоматизированном технологическом анализе. Символьные вычисления являются важнейшим компонентом, но не единственным, автоматизированного анализа. Вот почему тема ЭУП « Введение в проектирование систем автоматизированного технологического анализа», а ее первая часть посвящена символьным вычислениям.
Основой символьных вычислений является введение понятия «функция». Заметим, что понятие функции в данном случае используется более широко по сравнению с тем, как это принято в математике. Кроме того, функция используется не только при символьных вычислениях, но и при численных, а также при вычислениях в среде программирования.
С учетом выше сказанного пособие начинается с рассмотрения места функции в методах вычислений в MathCAD, рассматривается порядок создания функции и ее возможные имена. Затем рассматриваются основные математические операторы, используемые при символьных вычислениях. Далее в пособии приводятся примеры использования символьных вычислений.
Введение символьных вычислений позволяет рассмотреть в пособии проблему анализа на чувствительность, которая может быть составной частью системы автоматизированного технологического анализа.
Введение
Слайд 41
2
3.1
3.2
3.4.
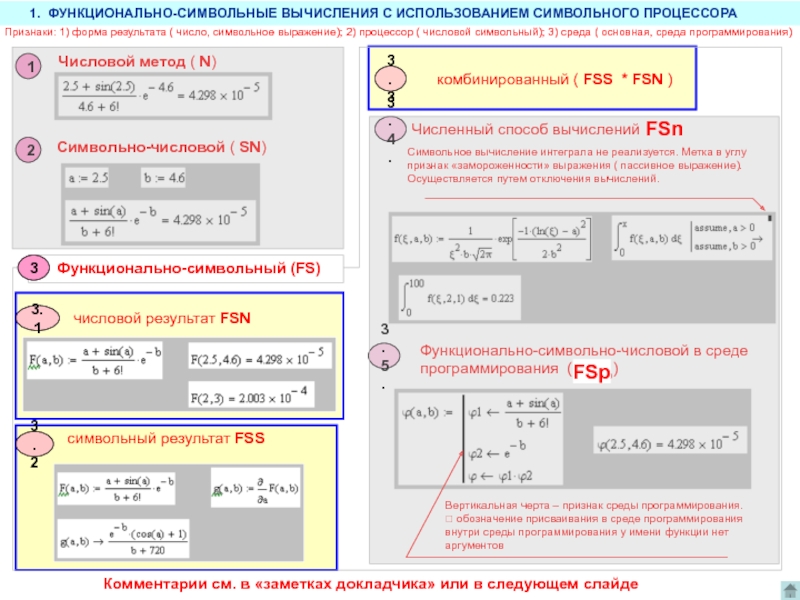
Числовой метод ( N)
Символьно-числовой ( SN)
числовой результат FSN
cимвольный результат
FSS 3.3
комбинированный ( FSS * FSN )
Функционально-символьно-числовой в среде
программирования ( СFS_p)
Численный способ вычислений
Символьное вычисление интеграла не реализуется. Метка в углу признак «замороженности» выражения ( пассивное выражение).
Осуществляется путем отключения вычислений.
Вертикальная черта – признак среды программирования.
обозначение присваивания в среде программирования внутри среды программирования у имени функции нет аргументов
Признаки: 1) форма результата ( число, символьное выражение); 2) процессор ( числовой символьный); 3) среда ( основная, среда программирования)
Функционально-символьный (FS)
3
3.5.
1. ФУНКЦИОНАЛЬНО-СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ СИМВОЛЬНОГО ПРОЦЕССОРА
Комментарии см. в «заметках докладчика» или в следующем слайде
FSn
FSp
Слайд 5----1. ОБЩАЯ ХАРАКТЕРИСТИКА ФУНКЦИОНАЛЬНО_СИМВОЛЬНЫХ ВЫЧИСЛЕНИЙ С ИСПОЛЬЗОВАНИЕМ CИМВОЛЬНОГО ПРОЦЕССОРА-----
Напомним, что
методы вычислений в среде MathCAD (МС) можно различать по следующим
признакам:- тип используемых компонентов в выражении ( числа, символы )
- форма результата ( число, символ );
- тип используемого процессора (числовой, символьный);
среда (основная, среда программирования ).
3. ФУНКЦИОНАЛЬНО – СИМВОЛЬНЫЙ МЕТОД ВЫЧИСЛЕНИЙ ------
В вариантах 3.1…..3.3. – используется символьное определение функции с получением числового результата ( FSN ), символьных вычислений с получением символьного результата ( FSS ), а также последовательное решение задач FSS*FSN. Последний тип задачи встречается наиболее часто.
3.1. После задания функции осуществляется ее числовой расчет путем подстановки в качестве аргументов числовых значений. Важно, что в этом случае сохраняется возможность символьных вычислений с определенной функцией ( в отличие от символьно-числового метода вычислений ). 3.2. После определения функции осуществляется символьное вычисление, например, частной производной по “a”. Результат вычислений - символьное выражение, которое выводится на дисплей ( знак символьного вывода результата – стрелка «-->» ).
3.3. Представляет последовательное использование п.3.2 и 3.1, что наиболее часто используется на практике.
3.4. Численный способ функционально-символьных вычислений ( В ДАННОМ ПОСОБИИ НЕ РАССМАТРИВАЕТСЯ).
Хотя выражение записано в виде функции f, но символьно вычислить интеграл не удается. Поэтому символьное вычисление переведено в разряд пассивных ( точка в модуле в правом верхнем углу). В этом случае интеграл вычисляется численно, однако пользователь фактически это не замечает этого, так как внешне форма записи не меняется. Однако, результат уже выводится с помощью знака равно "=" и будет числовым. Заметим, что при численных вычислениях MС реализует итерационный процесс по вычислению заданного выражения с определенной точностью с использованием того или иного численного метода ( по умолчанию эти параметры задаются, но могут быть скорректированы экспертом).
3.5. Вычисления в среде программирования ( В ДАННОМ ПОСОБИИ НЕ РАССМАТРИВАЕТСЯ).
В этом случае вычисления в MС осуществляются в среде программирования ( признак - вертикальная черта). Результат расчета числовой. Для присваивания используется знак обратной стрелки. К среде программирования приходится прибегать при наличии циклов в алгоритме и логических условий. Возникающий при этом объект записывается в виде функции, что позволяет легко реализовать расчеты при различных значениях входящих технологических параметров (a, b). При этом результат расчета - числовой.
Функционально-символьный метод позволяет перейти от числовых точечных расчетов к комплексному получению и исследованию математических моделей технологического объекта. Центр тяжести не только вычислений, но вывода математических моделей смещается в среду MathCAD. После разработки вычислительно-текстового документа вычислительного документа остается лишь сделать к нему текстовое описание. Возникающая в этом случае вычислительная система является комплексной, гибкой, предоставляет большую возможность для анализа технологической ситуации. Поэтому мы будем называть ее системой «Автоматизированного технологического анализа».
1. ФУНКЦИОНАЛЬНО-СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ СИМВОЛЬНОГО ПРОЦЕССОРА
Описание к предыдущему слайду ( из «заметок докладчика» )
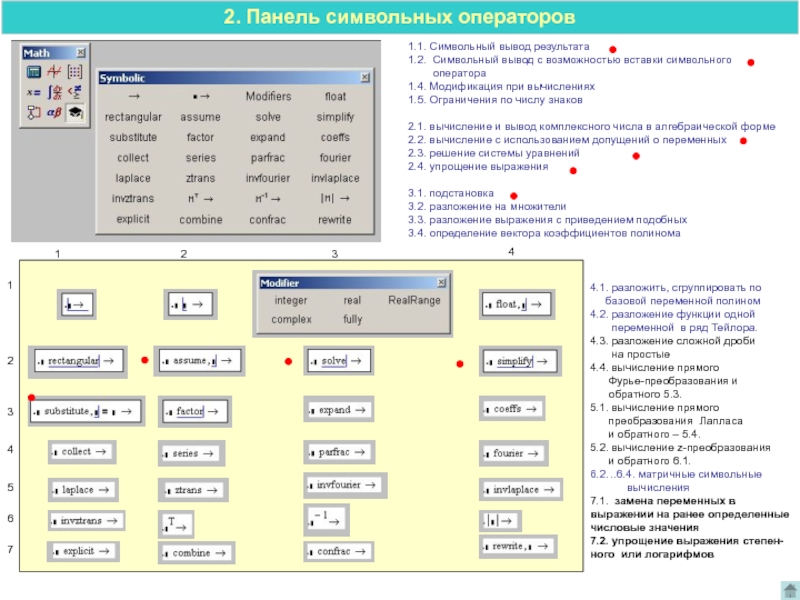
Слайд 61.1. Символьный вывод результата
1.2. Символьный вывод с возможностью вставки символьного
оператора
1.4. Модификация при вычислениях
1.5. Ограничения по
числу знаков2.1. вычисление и вывод комплексного числа в алгебраической форме
2.2. вычисление с использованием допущений о переменных
2.3. решение системы уравнений
2.4. упрощение выражения
3.1. подстановка
3.2. разложение на множители
3.3. разложение выражения с приведением подобных
3.4. определение вектора коэффициентов полинома
2. Панель символьных операторов
4.1. разложить, сгруппировать по
базовой переменной полином
4.2. разложение функции одной
переменной в ряд Тейлора.
4.3. разложение сложной дроби
на простые
4.4. вычисление прямого
Фурье-преобразования и
обратного 5.3.
5.1. вычисление прямого
преобразования Лапласа
и обратного – 5.4.
5.2. вычисление z-преобразования
и обратного 6.1.
6.2…6.4. матричные символьные
вычисления
7.1. замена переменных в
выражении на ранее определенные
числовые значения
7.2. упрощение выражения степен-
ного или логарифмов
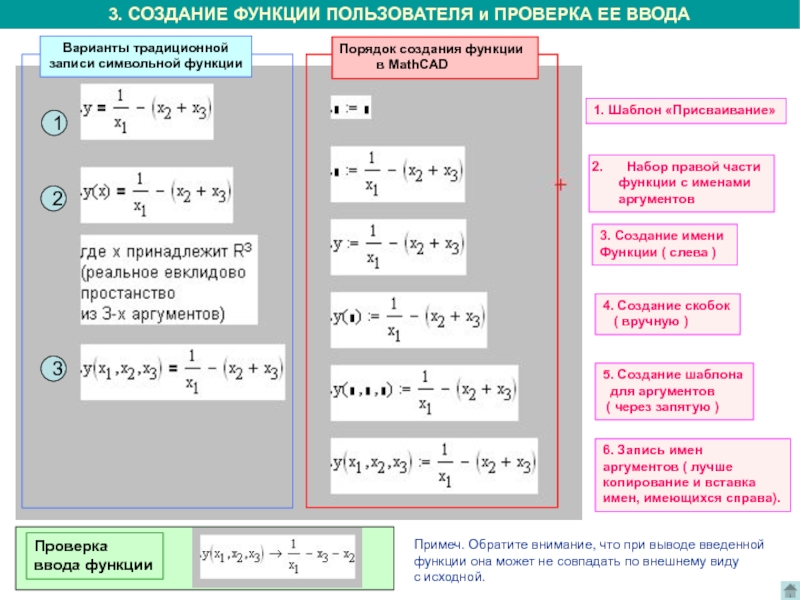
Слайд 73. СОЗДАНИЕ ФУНКЦИИ ПОЛЬЗОВАТЕЛЯ и ПРОВЕРКА ЕЕ ВВОДА
Варианты традиционной
записи
символьной функции
1
2
3
Порядок создания функции
в
MathCAD1. Шаблон «Присваивание»
Набор правой части
функции с именами
аргументов
3. Создание имени
Функции ( слева )
4. Создание скобок
( вручную )
5. Создание шаблона
для аргументов
( через запятую )
6. Запись имен
аргументов ( лучше
копирование и вставка
имен, имеющихся справа).
Проверка
ввода функции
Примеч. Обратите внимание, что при выводе введенной
функции она может не совпадать по внешнему виду
с исходной.
Слайд 83. СОЗДАНИЕ ФУНКЦИИ ПОЛЬЗОВАТЕЛЯ и ПРОВЕРКА ЕЕ ВВОДА
Примеры создания функций:
Обычная
запись
Запись в MathCAD
Проверка в MathCAD
Пример 1
Пример 2
В функции введено избыточное
число аргументов,
Исключается возможность
символьных вычислений
для z.
неудачный вариант определения функции
Пример 3
Пример 4
Составная функция в символьном виде
не выводится и не может использоваться
для символьных вычислений.
Приходится отдельно вести символьные
вычисления для каждой ее компоненты.
Задание и вывод функции плотности
вероятности нормального распределения
(распределения Гаусса). μ – математичес-
кое ожидание,σ – среднеквадратическое
отклонение
встроенная в MathCAD функция плотности вероятности
в символьном виде не выводится
Слайд 94. Точечные числовые вычисления с использованием
функционально-символьной модели
Точечный числовой расчет
легко реализуется путем подстановки вместо соответствующих
переменных ( аргументов) их
числовых значений ( не забудьте учесть размерности переменных ! ). Дальнейшие примеры будем реализовывать в рамках листинга 1.
Листинг 1.
Слайд 10Проверка правильности ввода функции с использованием simplify
5. УПРОЩЕНИЕ ВЫРАЖЕНИЙ ( Simplify )
Получение
символьного
нуля - признак
совпадения
выражений
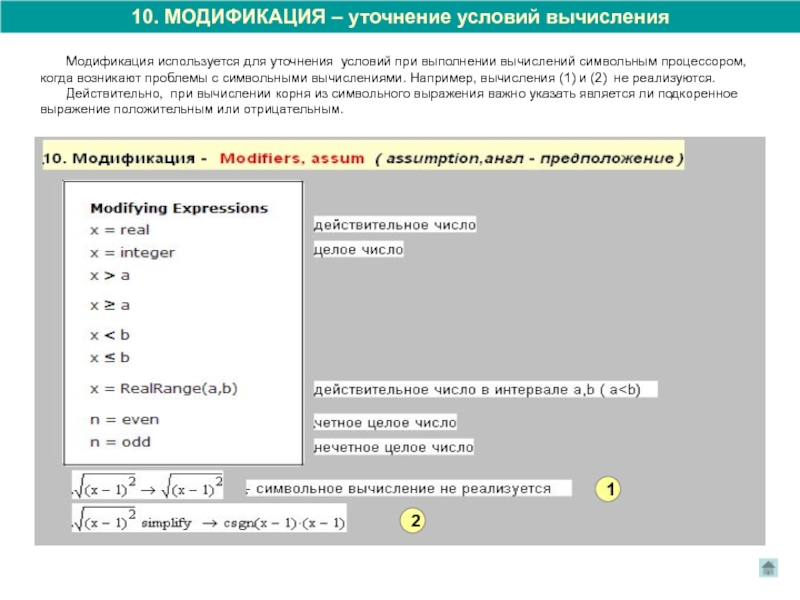
Слайд 1510. МОДИФИКАЦИЯ – уточнение условий вычисления
Модификация используется для уточнения условий при выполнении вычислений символьным процессором,
когда возникают проблемы с символьными вычислениями. Например, вычисления (1) и (2) не реализуются.
Действительно, при вычислении корня из символьного выражения важно указать является ли подкоренное
выражение положительным или отрицательным.
1
2
Слайд 17
11.
СИМВОЛЬНОЕ РЕШЕНИЕ УРАВНЕНИЙ Возможность символьного решения уравнений важна, так как на начальном этапе технологического анализа
составляются скалярные (одиночные) уравнения или системы уравнений на основе материального баланса, баланса сил
и т.д. Решая их относительно интересующего нас технологического параметра, мы получаем расчетные формулы.
Ниже рассматриваются примеры символьного решения уравнений в среде MathCAD.
Слайд 18
11. СИМВОЛЬНОЕ РЕШЕНИЕ
УРАВНЕНИЙ Достоинство
решения линейных символьных уравнений матричным методом: отсутствие «разрыва» в
вычислительном процессе.
То есть при изменении матрицы A и вектора С результат
получается автоматически ( см (1)).
1
Слайд 19ПРИМЕРЫ
ВЫПОЛНЕНИЯ СИМВОЛЬНЫХ ВЫЧИСЛЕНИЙ
И СИМВОЛЬНОГО АНАЛИЗА
12.1. Деформация основной нити
при зевообразовании
12.2. Вывод и расчет объема ровничной паковки
12.3. Линейная плотность
слоя, поступающего в машинуСлайд 20 12.1. ДЕФОРМАЦИЯ
ОСНОВНОЙ НИТИ ПРИ ЗЕВООБРАЗОВАНИИ
Обратите внимание, что числовой расчет ( точечный
расчет ) реализуется путем подстановки в функцию вместо соответствующих параметров их числовых значений. Такой способ точечных расчетов сохраняет
возможность дальнейших символьных вычислений для функциональной модели.
Слайд 26
13. АНАЛИЗ
НА ЧУВСТВИТЕЛЬНОСТЬ Пусть имеется функциональная математическая модель y(x1,x2,x3..), устанавливающая связь технологического
критерия y c факторами. Например, в примере при расчете деформации нити при зевообразовании ( см ранее )
в качестве критерия выступает деформация нити, а в качестве факторов геометрические параметры зева.
Пусть технологический объект имеет некоторые параметры заправки, которые характеризуются набором
значений факторов xo=(x1o, x2o….)T. Будем делать отклонения Δх от рабочей точки. Построим вектор отношений,
вектор абсолютной чувствительности (АЧ). Как видно, вектор абсолютной чувствительности совпадает
при малых отклонениях с понятием градиента.
Вектор АЧ является размерным. Перейдем к безразмерному вектору относительной чувствительности.
Вектор абсолютной
чувствительности
Относительная
чувствительность
для i –го фактора.
Распространяя полученные результаты на несколько критериев, получаем матрицу чувствительности.
Относительная чувствительность к i-ому фактору показывает на сколько процентов изменится выходной
технологический критерий, если относительное изменение i-го фактора равно 1%. Знак чувствительности
указывает на характер влияния фактора на критерий при малых отклонениях от рабочей точки xo.
Слайд 27
13. АНАЛИЗ
НА ЧУВСТВИТЕЛЬНОСТЬРасчет чувствительности в MathCAD
Для степенной функции
чувствительность не зависит
от выбора рабочей точки
и равна показателю степени
в функциональной модели.
Слайд 2814. АНАЛИЗ ФУНКЦИОНАЛЬНОЙ МОДЕЛИ В ВИДЕ ПОЛИНОМА ВТОРОГО ПОРЯДКА
1
Модель (1) в виде полинома второго
порядка содержит факторы
x1 и x2, посредством которых можно влиять
на критерий y. ( Примеч. Переход к полиному
второго порядка для произвольной функции
приведено в приложении ).
Пусть кроме того коэффициенты a и b
не известны. Назовем их параметрами.
В результате имеем факторно-параметричес-
кую модель Рассмотрим основные этапы
ее анализа.
П.3…5 позволяют найти стационарную точку,
то есть точку, где функция может иметь
оптимум. Для ее нахождения необходимо
вычислить градиент и решить систему
уравнений исходя из условия равенств
градиента нуль вектору.
Из 5 видно, что стационарная такая точка
существует и она зависит от параметров a,b
модели.
Учитывая это возникает задача анализа на
чувствительность стационарной точки
к параметрам.
Слайд 2914. АНАЛИЗ ФУНКЦИОНАЛЬНОЙ МОДЕЛИ В ВИДЕ ПОЛИНОМА ВТОРОГО ПОРЯДКА
В п.7
реализуем анализ на чувствительность. В п.7.1 вычисляется
чувствительность. В качестве критериев
используются найденные стационарные точки.В результате получаются функции чувствительности.
В п. 7.3. осуществляется точечный расчет чувствительности для конкретной тоски ( 1,2).
Как видно наиболее сильное влияние
для данной очки относится к параметру b для критерия X2o. При этом с ростом этого параметра значение стационарной очки уменьшается.
Наиболее слабое влияние оказывает
параметр b на критерий x1o. При этом с ростом параметра b х1о уменьшается.
Слайд 30 Дальнейшее исследование направлено на проверку наличия оптимума у
функции в найденной стационарной точке.
Можно показать, что для этого необходимо
рассмотреть матрицу вторых производных. Поэтому она вычисляется в п. 8.
Далее для проверки на минимум функции необходимо вычислить главные миноры ( определители на главной
диагонали) ( см. п.9 ). Для получения минимума в стационарной точке эти определители должны быть положительны. В результате находим условие, определяющее соотношение между параметрами a и b, которое
обеспечивает минимум функциональной модели ( 1 ) ( см. выводы).
14. АНАЛИЗ ФУНКЦИОНАЛЬНОЙ МОДЕЛИ В ВИДЕ ПОЛИНОМА ВТОРОГО ПОРЯДКА
Слайд 3115. ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
Набрать и отладить листинг 1 ( п. 4….11).
Сделать необходимые для себя комментарии и пояснения.
Набрать листинг
2 в MathCAD « Анализ полиномиальной 2-х факторной полиномиальной модели» ( см. п. 15 ) с анализом на чувствительность к параметрам для следующих исходных данных, приведенных ниже.Оформить отчет на основе листинга 2.
Слайд 36 Получение модели в виде полинома второго порядка
на основе
разложения функции в ряд Тейлора
Полином второго порядка
может использоваться для получения математических моделей на основе обработки результатов эксперимента в том случае, если отклонения от некоторой базовой точки xo не очень велики.
Основой для использования полинома второго порядка является разложение функции в ряд Тейлора с ограничением
двух членов ряда. Рассмотрим более подробно это на примере функции 2-х переменных.