ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

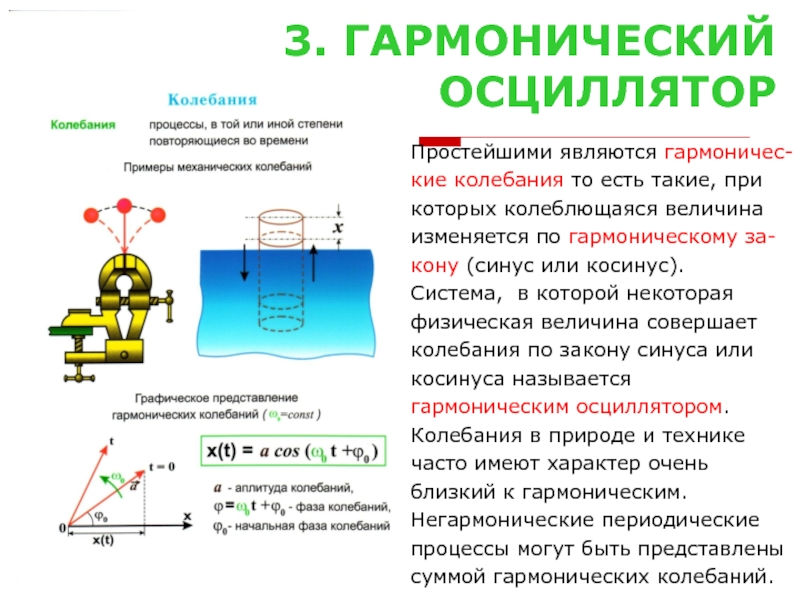
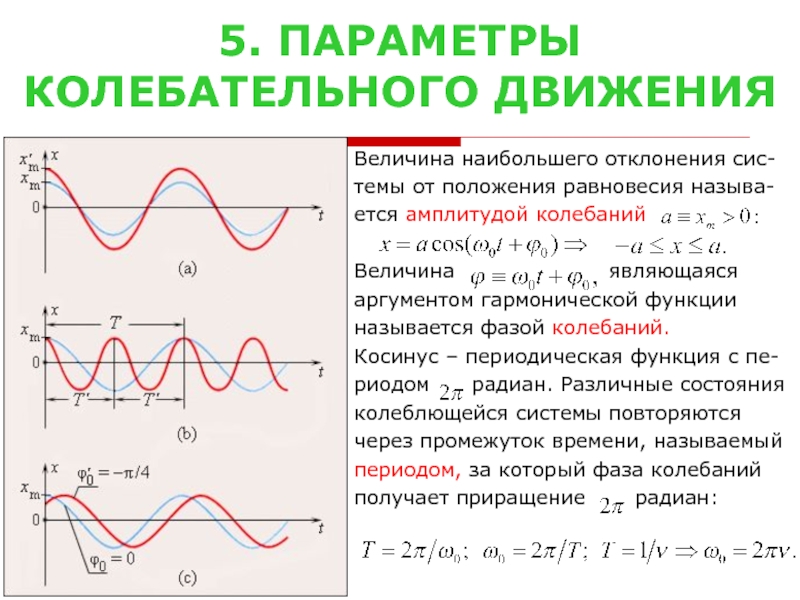
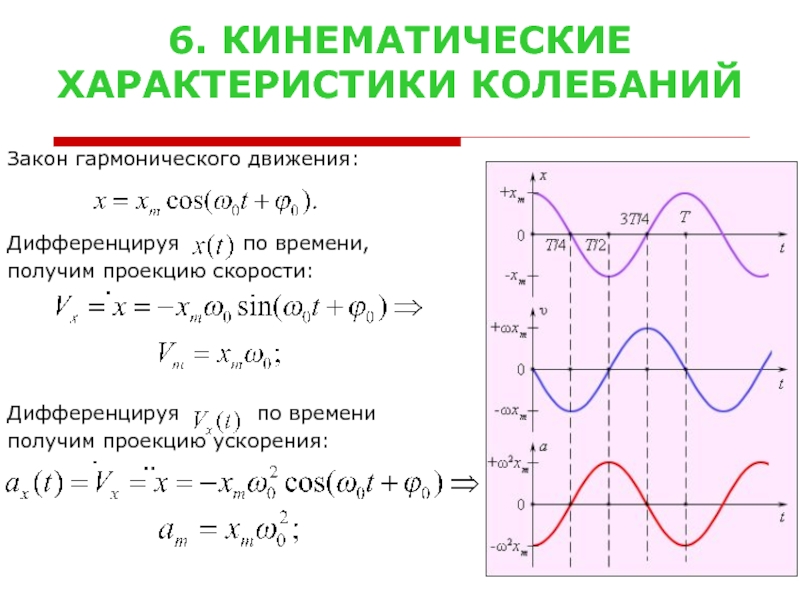
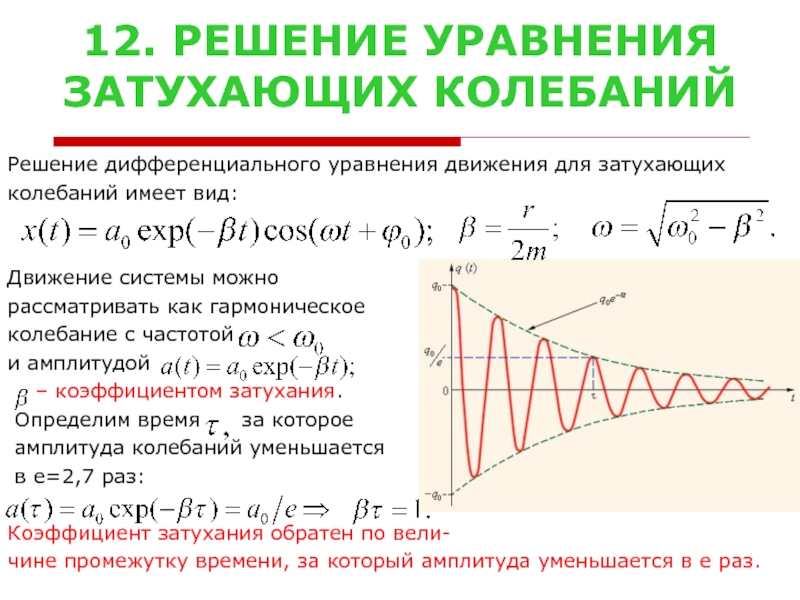
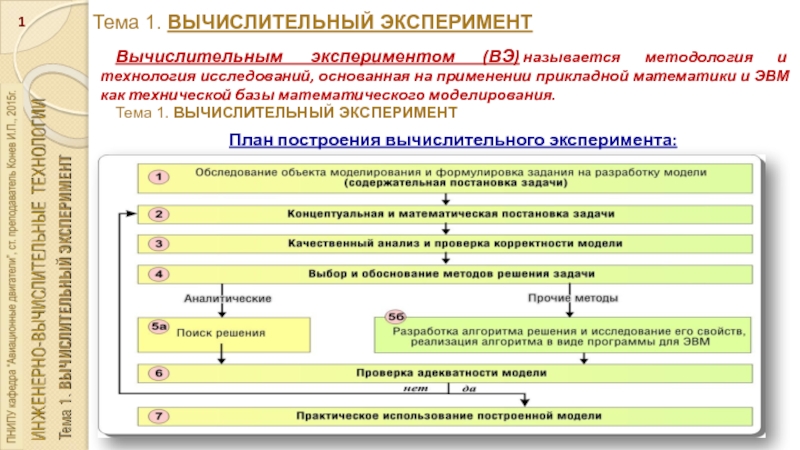
зависимости от физической природы
повторяющегося процесса различают:
механические колебания – колебания

зданий, деталей машин, маятников, струн,
камертонов, частиц среды;
электромагнитные колебания – колебания
напряжения на обкладках конденсатора и
силы тока в катушке колебательного кон-
тура радиоприемника;
экономические, демографические, популя-
ционные, климатические колебания.

(собственные)
колебания, вынужденные колебания,
автоколебания и параметрические
колебания.
Свободными (или собственными), на-
зываются колебания,

которые проис-
ходят в системе, предоставленной
самой себе после того, как она была
выведена из положения равновесия.
Вынужденными называются колебания,
в процессе которых колеблющаяся
система подвергается воздействию
внешней периодической силы.

колеблющаяся величина
изменяется по гармоническому за-
кону (синус или косинус).
Система, в которой

некоторая
физическая величина совершает
колебания по закону синуса или
косинуса называется
гармоническим осциллятором.
Колебания в природе и технике
часто имеют характер очень
близкий к гармоническим.
Негармонические периодические
процессы могут быть представлены
суммой гармонических колебаний.

амплитудой колебаний

Величина

являющаяся
аргументом гармонической функции
называется фазой колебаний.
Косинус – периодическая функция с пе-
риодом радиан. Различные состояния
колеблющейся системы повторяются
через промежуток времени, называемый
периодом, за который фаза колебаний
получает приращение радиан:

времени,
получим проекцию скорости:




Дифференцируя по

времени
получим проекцию ускорения:

является консервативной. Ей отвечает
потенциальная энергия

полная энергия гармонических
колебаний должна оставаться неизменной.

Рассмотрим

систему, состоящую из тела массой
подвешенного на пружине, массой которой можно
пренебречь.
В положении равновесия сила тяжести
уравновешивается упругой силой
Будем характеризовать смещение шарика из поло-
жения равновесия координатой причем ось
направим вертикально вниз, а нуль оси совместим
с положением равновесия шарика.
Если сместить шарик в положение, характеризуемое координатой то
удлинение пружины станет равным а проекция результирующей
силы примет значение

Маятником называют тело, совершающее колебания под действием силы тяжести.

малые колебания относительно оси, не проходящей через его центр масс.

сопротивления,
действие которых приводит к затуханию колебаний.
В простейшем и

наиболее часто
встречающемся случае сила сопротив-
ления пропорциональна скорости:

вид:


Движение системы можно
рассматривать как гармоническое
колебание с частотой

и амплитудой
– коэффициентом затухания.
Определим время за которое
амплитуда колебаний уменьшается
в e=2,7 раз:

Коэффициент затухания обратен по вели-
чине промежутку времени, за который амплитуда уменьшается в e раз.

период, называют декрементом затухания




Логарифм отношения амплитуд, отстоящих на период,

называется
логарифмическим декрементом затухания

называемая добротностью.






Добротность в раз превышает число колебаний

совершаемых
системой за время в течение которого амплитуда колебаний уменьшается в раз.

потенциальной энергии, то есть
Для затухающих колебаний
Скорость изменения энергии

системы равна мощности, развиваемой силой сопротивления:

В моменты времени, для которых скорость тела равна нулю мощность силы сопротивления также равна нулю.

Во все остальные моменты мощность отрицательна и энергия убывает.

сила сопротивления

внешняя
гармоническая вынуждающая сила с амплитудой
Уравнение движения в данном случае будет иметь вид:




– амплитуда ускорения и частота внешней вынуждающей силы.

математической теореме, общее решение неоднород-
ного дифференциального уравнения равно сумме общего

решения соот-
ветствующего однородного уравнения и частного решения неоднородного
уравнения, то есть

– частота свободных
затухающих колебаний.

заметную роль только в начальной стадии процесса, при
установлении колебаний. С

течением времени из-за множителя
роль первого слагаемого уменьшается и им
можно пренебречь, оставляя в решении лишь
второе слагаемое. Оно представляет собой
гармоническое колебание с частотой внешней
вынуждающей силы

частоты вынуждаю-
щей силы приводит к тому, что при некоторой определенной

для данной
системы частоте амплитуда достигает максимального значения. Это явле-
ние называется резонансом, а соответствующая частота - резонансной.

Резонансную частоту определим из условия
максимального значения амплитуды или
минимального значения для подкоренного
выражения в знаменателе. Продифференцировав
это выражение по и приравняв нулю, получим
условие, определяющее резонансную частоту:

взаимно перпендикулярных
колебаниях одной частоты. Пусть колебания вдоль оси

происходят с
нулевой начальной фазой, а вдоль оси со сдвигом по фазе на
Тогда уравнения колебаний примут вид:

Чтобы получить уравнение траектории в явном виде исключим время
Из первого уравнения следует, что

Подставляя синус и косинус в формулу
для получим:

уравнение эллипса. Полуоси
этого эллипса в общем случае
не совпадают с осями координат.

результирующего колебания для
некоторых частных случаев.
Пусть

В этом случае общее уравнение траектории

принимает вид
Движение
является гармоническим
колебанием вдоль прямой
с амплитудой

2. Пусть В этом случае

Траектория является прямой, лежа-
щей во 2-м и 4-м квадрантах.

общее
уравнение траектории
принимает вид
Это уравнение эллипса, приведенного
к

координатным осям, причем полуоси
эллипса равны соответствующим
амплитудам колебаний.

При
движение против
часовой стрелки.

При
движение по
часовой стрелке

для
соответствует движению против часовой стрелки, знак «-» – движению

по часовой стрелке.

принимает вид

При равенстве амплитуд
эллипс вырождается
в окружность.
Это означает что равномерное
движение по окружности
радиуса с угловой
скоростью может быть
представлена как сумма двух
взаимно перпендикулярных
колебаний