Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гармонический анализ непериодических сигналов
Содержание
- 1. Гармонический анализ непериодических сигналов
- 2. Подставив (2.2) в (2.1), получимПри Т→∞ ω1=2π/T→0,
- 3. Подставив (2.2) в (2.1), получим (2.3)называется спектральной плотностью или спектральнойхарактеристикой функции s(t).Внутренний интеграл, являющийся функцией ω,(2.4)(2.5)
- 4. В общем случае , когда пределы t1
- 5. Выражение (2.6) отличается от (1.13) только отсутствием
- 6. На основании формулы (2.8) нетрудно получить тригонометрическуюформу
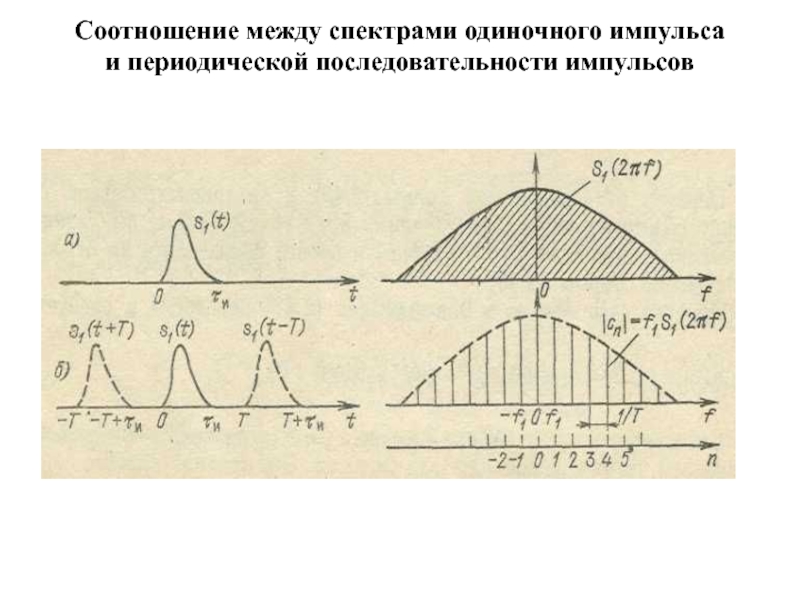
- 7. Соотношение между спектрами одиночного импульса и периодической последовательности импульсов
- 8. Коэффициент n-й гармоники в соответствии с выражением
- 9. Модуль спектральной плотности одиночного импульса иогибающая линейчатого
- 10. Скачать презентанцию
Подставив (2.2) в (2.1), получимПри Т→∞ ω1=2π/T→0, а спектр – сплошным.Поэтому в выражении (2.3) можно заменить ω1 на dω, nω на текущую частоту ω, а операцию суммированияоперацией интегрирования (2.3)называется спектральной плотностью
Слайды и текст этой презентации
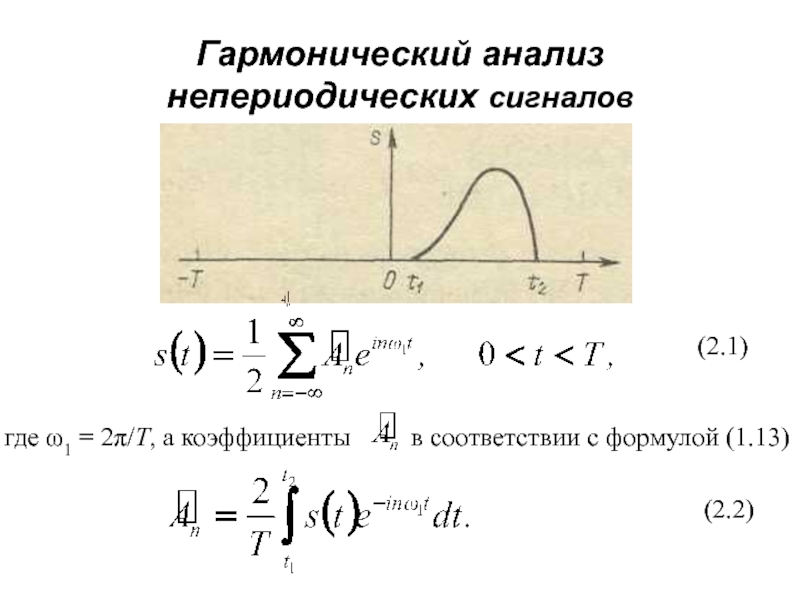
Слайд 1Гармонический анализ непериодических сигналов
где ω1 = 2π/T, а коэффициенты
в соответствии с формулой (1.13)
Слайд 2
Подставив (2.2) в (2.1), получим
При Т→∞ ω1=2π/T→0, а спектр –
сплошным.
Поэтому в выражении (2.3) можно заменить ω1 на dω,
nω
на текущую частоту ω, а операцию суммированияоперацией интегрирования
(2.3)
называется спектральной плотностью или спектральной
характеристикой функции s(t).
Внутренний интеграл, являющийся функцией ω,
(2.4)
(2.5)
Слайд 3
Подставив (2.2) в (2.1), получим
(2.3)
называется спектральной плотностью или спектральной
характеристикой
функции s(t).
Внутренний интеграл, являющийся функцией ω,
(2.4)
(2.5)
Слайд 4В общем случае , когда пределы t1 и t2 не
уточнены,
спектральная плотность записывается в форме
После подстановки (2.6) в выражение
(2.4) получаемВыражения (2.6) и (2.7) называются соответственно
прямым и обратным преобразованиями Фурье.
(2.7)
(2.6)
Слайд 5Выражение (2.6) отличается от (1.13) только отсутствием множителя
2/Т. Следовательно, спектральная
плотность обладает
всемиосновными свойствами коэффициентов комплексного ряда
Фурье. Используя (1.10) и (1.11), по аналогии с можно написать
Модуль и аргумент спектральной плотности определяются
выражениями
(2.8)
(2.9)
(2.10)
(2.11)
Выражения (2.10) и (2.11) - АЧХ и ФЧХ сплошного спектра непериодического сигнала s(t).
Слайд 6На основании формулы (2.8) нетрудно получить тригонометрическую
форму интегрального преобразования (2.7):
Отметим,
что при ω=0 выражение (2.5) переходит в следующее:
(2.12)
(2.13)
Слайд 8
Коэффициент n-й гармоники в соответствии с выражением (1.13)
Спектральная же плотность
одиночного импульса на той же
частоте ω= nω1 будет [см. (2.5)]
Для
комплексной амплитуды n-ой гармоники имеет местопростое соотношение
Слайд 9Модуль спектральной плотности одиночного импульса и
огибающая линейчатого спектра периодической
последовательности, полученной
путем повторения заданного
импульса, совпадают по форме и отличаются только
масштабом.
На рис.
2.2,б штриховой линией обозначена огибающаялинейчатого спектра An/2=|cn|=f1 S1(nω1).
При Т→∞, приходим к одиночному импульсу со спектральной
плотностью
Таким образом, становится наглядным термин «спектральная
плотность»: S(ω) есть амплитуда напряжения (тока),
приходящаяся на 1 Гц в бесконечно узкой полосе частот,
которая включает в себя рассматриваемую частоту ω.
