Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия
Содержание
- 1. Геометрия
- 2. План:Вопрос 1. Основные понятия геометрии.Вопрос 2. Планиметрия.Вопрос 3. Стереометрия.
- 3. Вопрос 1. Основные понятия геометрии
- 4. Геометрия Геометрия - это раздел математики, изучающий
- 5. Планиметрия Планиметрия изучает фигуры и их свойства
- 6. СтереометрияСтереометрия изучает фигуры и их свойства в
- 7. Вопрос 2. Планиметрия
- 8. К основным геометрическим фигурам на плоскости относятся
- 9. ТочкаТочка — абстрактный объект в пространстве, обладающий
- 10. ЛинияПрямую линию, или прямую, можно представить себе
- 11. Если две прямые пересекаются под прямым углом,
- 12. ЛучЛуч — это направленная полупрямая, которая имеет точку начала и не имеет конца.Луч изображается так:
- 13. Ломаная линия Ломаная линия — это несколько
- 14. ПлоскостьПлоскость, как и прямая, — это первичное
- 15. УголУглом называется фигура, которая состоит из точки
- 16. Виды углов
- 17. УголДва угла называются смежными, если одна сторона
- 18. КвадратКвадрат – правильный четырёхугольник, у которого все
- 19. ПрямоугольникПрямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам). Противоположные стороны прямоугольника попарно равныАCD
- 20. Параллелограмм Параллелограмм - это четырехугольник у которого
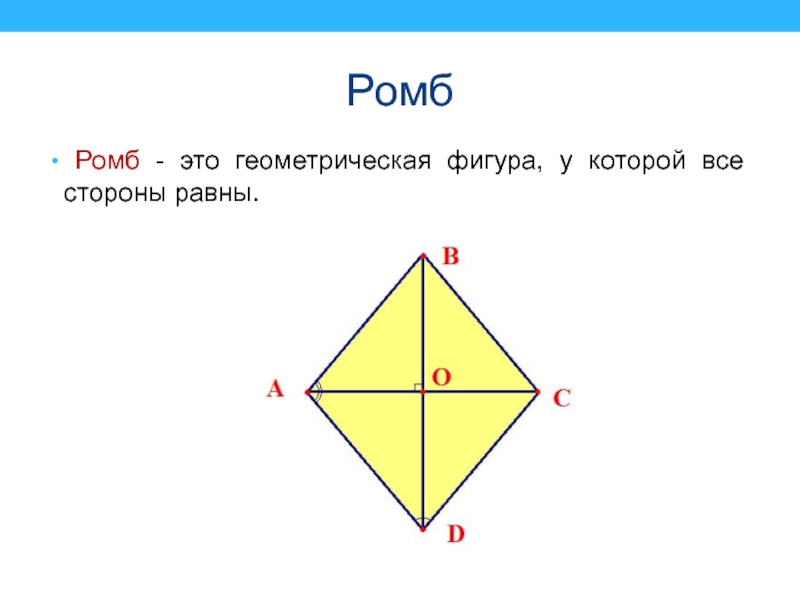
- 21. Ромб Ромб - это геометрическая фигура, у которой все стороны равны.
- 22. ТрапецияТрапеция — четырехугольник, у которого только две
- 23. ОкружностьОкружность — замкнутая плоская кривая, все точки
- 24. ТреугольникТреугольник — простейший многоугольник, имеющий 3 вершины
- 25. Виды треугольниковВиды треугольников по углам:Остроугольный треугольник —
- 26. Виды треугольниковВиды треугольников по сторонам:Равносторонний треугольник (или
- 27. Многоугольник Многоугольник — это геометрическая фигура, обычно
- 28. Вопрос 3. Стереометрия
- 29. ПризмаПризмой называется многогранник, у которого две стороны
- 30. ПризмаЕсли боковые ребра призмы находятся под некоторым углом к основанию, то призма является наклонной.
- 31. ПараллелепипедПризма, у которой основание есть параллелограмм, называется
- 32. ПараллелепипедПрямой параллелепипед, у которого основание является прямоугольником, называется прямоугольным.Прямоугольный параллелепипед
- 33. ПирамидаПирамидой называется многогранник, который состоит из многоугольника
- 34. Правильные многогранникиЕсли выпуклый многогранник имеет все грани
- 35. Тетраэдр это многогранник, у которого грани правильные
- 36. ЦилиндрЦилиндр представляет собой тело, состоящее из двух
- 37. КонусКонусом называется тело, которое состоит из круга
- 38. ШарШар это геометрическое тело, состоящее из всех
- 39. Скачать презентанцию
План:Вопрос 1. Основные понятия геометрии.Вопрос 2. Планиметрия.Вопрос 3. Стереометрия.
Слайды и текст этой презентации
Слайд 4Геометрия
Геометрия - это раздел математики, изучающий пространственные структуры и
отношения, а также их обобщения.
Слайд 5Планиметрия
Планиметрия изучает фигуры и их свойства на плоскости. Образно
говоря, планиметрия изучает всё, что можно нарисовать или начертить на
листе бумаги.Основные объекты планиметрии - это точки, линии и замкнутые фигуры (например - квадрат, треугольник, круг, трапеция, ромб).
Множество всех точек, рассматриваемых в планиметрии образует плоскость.
Множество точек в планиметрии называется фигурой.
Замкнутая фигура в планиметрии - это множество точек, ограниченных линией.
Слайд 6Стереометрия
Стереометрия изучает фигуры и их свойства в пространстве. Образно говоря,
стереометрия изучает всё, что можно склеить из бумаги, сколотить из
досок, построить из кирпичей и т.п.Основными объектами стереометрии являются точки, прямые, плоскости и замкнутые пространственные фигуры (например - куб, пирамида, параллелепипед, шар, конус).
Множество всех точек, рассматриваемых в стереометрии, называется пространством.
Любое множество точек называется фигурой.
Замкнутая фигура в стереометрии - это множество точек, ограниченных поверхностью.
Слайд 8К основным геометрическим фигурам на плоскости относятся точка и прямая
линия.
Отрезок, луч, ломаная линия — простейшие геометрические фигуры на
плоскости.Слайд 9Точка
Точка — абстрактный объект в пространстве, обладающий координатами, но не
имеющий размеров, массы, направленности и каких-либо других геометрических или физических
характеристик. Одно из фундаментальных понятий в математике и физике.Точка — это самая малая геометрическая фигура, которая является основой всех прочих построений в любом изображении или чертеже.
Слайд 10Линия
Прямую линию, или прямую, можно представить себе как бесчисленное множество
точек, которые расположены на одной линии, не имеющей ни начала,
ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна.Прямая изображается так:
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком.
Отрезок изображается так:
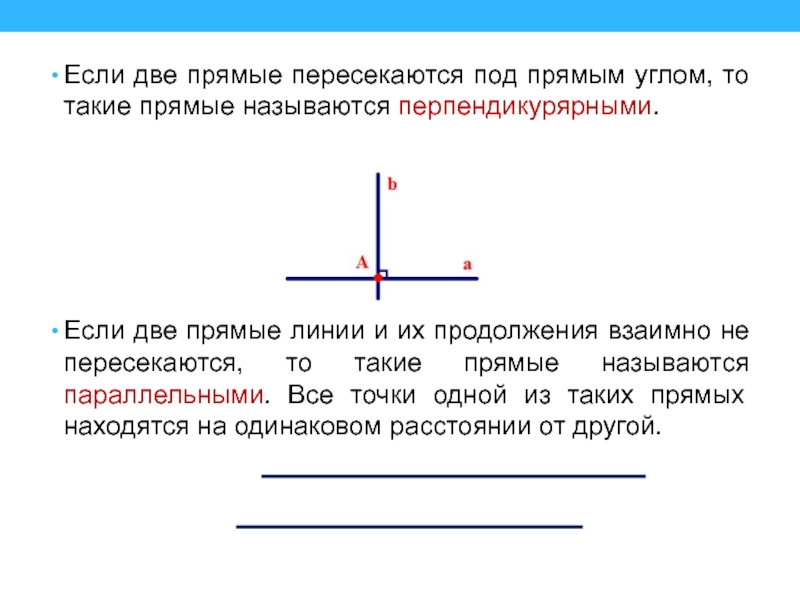
Слайд 11Если две прямые пересекаются под прямым углом, то такие прямые
называются перпендикурярными.
Если две прямые линии и их продолжения взаимно не
пересекаются, то такие прямые называются параллельными. Все точки одной из таких прямых находятся на одинаковом расстоянии от другой.Слайд 12Луч
Луч — это направленная полупрямая, которая имеет точку начала и
не имеет конца.
Луч изображается так:
Слайд 13Ломаная линия
Ломаная линия — это несколько отрезков, соединенных между
собой так, что конец первого отрезка является началом второго отрезка,
а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку), отрезки расположены не на одной прямой.Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.
Ломаная линия изображается так:
Если конец последнего отрезка
ломаной совпадает с началом
первого отрезка, то такая ломаная линия называется замкнутой.
Слайд 14Плоскость
Плоскость, как и прямая, — это первичное понятие, не имеющее
определения. У плоскости, как и у прямой, нельзя видеть ни
начала, ни конца.Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
Слайд 15Угол
Углом называется фигура, которая состоит из точки – вершины угла
– и двух различных полупрямых, исходящих из этой точки, -
сторон угла.Угол равный 90° называется прямым.
Меньше 90° - острым.
Больше 90° - тупым.
Слайд 17Угол
Два угла называются смежными, если одна сторона у них общая,
а другие их стороны являются дополнительными полупрямыми. Сумма смежных углов
равна 180°.Если стороны одного угла являются дополнительными полупрямыми сторон другого угла, то такие углы называются вертикальными.
Слайд 18Квадрат
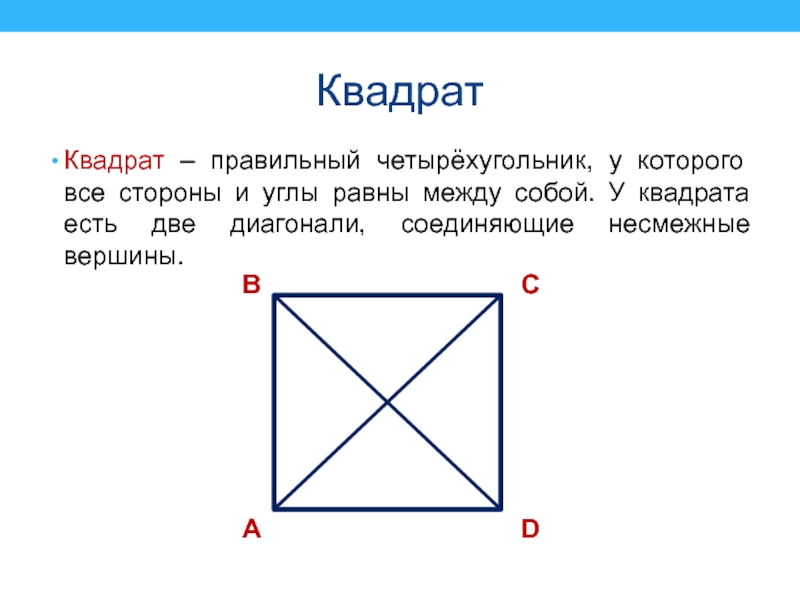
Квадрат – правильный четырёхугольник, у которого все стороны и углы
равны между собой. У квадрата есть две диагонали, соединяющие несмежные
вершины.А
B
C
D
Слайд 19Прямоугольник
Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90
градусам). Противоположные стороны прямоугольника попарно равны
А
C
D
Слайд 20Параллелограмм
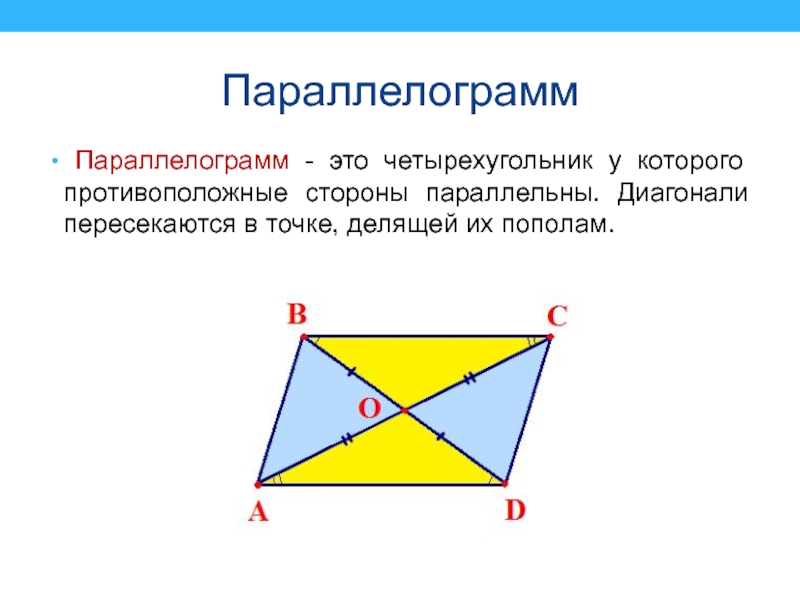
Параллелограмм - это четырехугольник у которого противоположные стороны параллельны.
Диагонали пересекаются в точке, делящей их пополам.
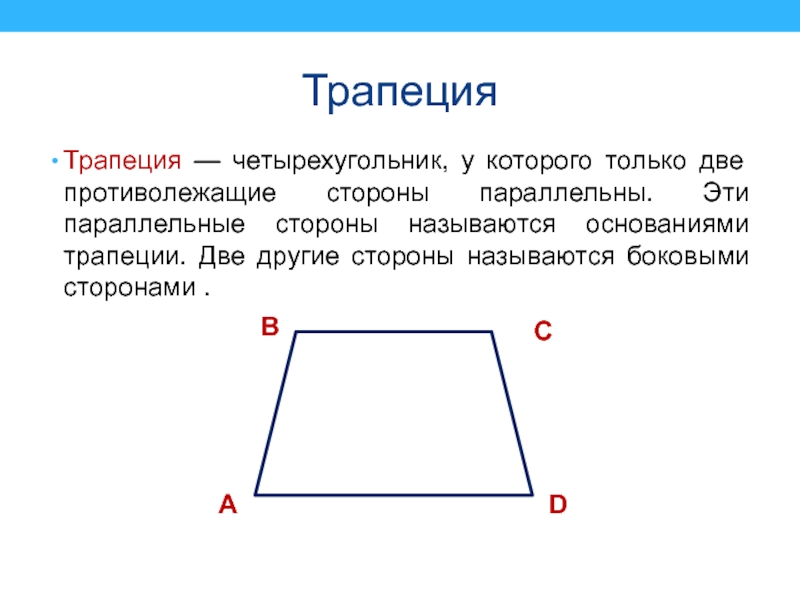
Слайд 22Трапеция
Трапеция — четырехугольник, у которого только две противолежащие стороны параллельны.
Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются
боковыми сторонами .D
C
B
A
Слайд 23Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены
от данной точки (центра окружности), лежащей в той же плоскости,
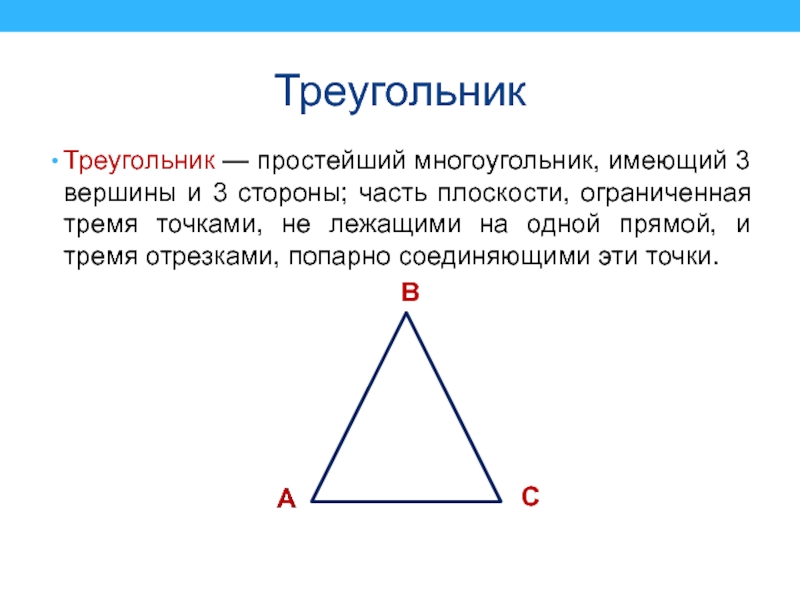
что и кривая.Слайд 24Треугольник
Треугольник — простейший многоугольник, имеющий 3 вершины и 3 стороны;
часть плоскости, ограниченная тремя точками, не лежащими на одной прямой,
и тремя отрезками, попарно соединяющими эти точки.B
C
Слайд 25Виды треугольников
Виды треугольников по углам:
Остроугольный треугольник — это треугольник, все
углы которого острые (то есть градусная мера каждого угла меньше
90º).Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).
Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).
Слайд 26Виды треугольников
Виды треугольников по сторонам:
Равносторонний треугольник (или правильный треугольник) —
это треугольник, у которого все три стороны равны.
Равнобедренный треугольник —
это треугольник, у которого две стороны равны.Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.
Слайд 27Многоугольник
Многоугольник — это геометрическая фигура, обычно определяется как замкнутая
ломаная без самопересечений, однако иногда самопересечения допускаются.
Вершины ломаной называются вершинами
многоугольника, а отрезки — сторонами многоугольника. Слайд 29Призма
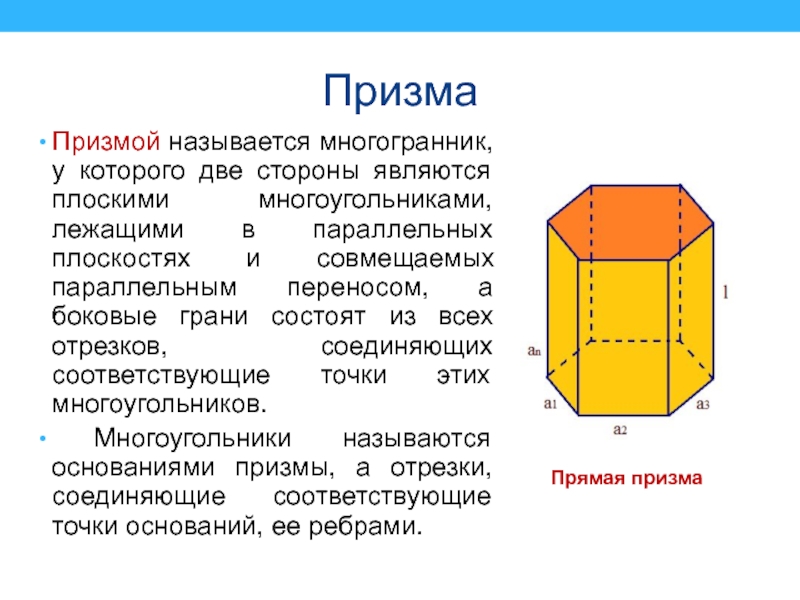
Призмой называется многогранник, у которого две стороны являются плоскими многоугольниками,
лежащими в параллельных плоскостях и совмещаемых параллельным переносом, а боковые
грани состоят из всех отрезков, соединяющих соответствующие точки этих многоугольников.Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие точки оснований, ее ребрами.
Прямая призма
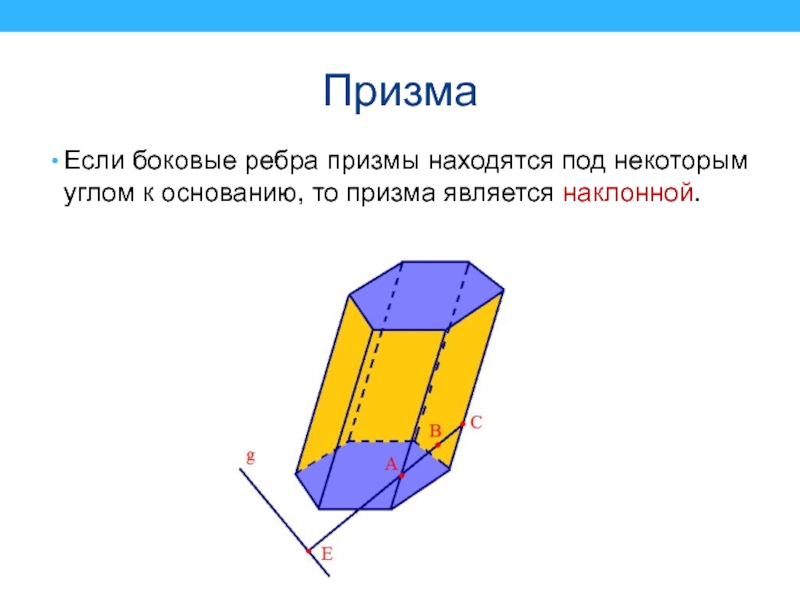
Слайд 30Призма
Если боковые ребра призмы находятся под некоторым углом к основанию,
то призма является наклонной.
Слайд 31Параллелепипед
Призма, у которой основание есть параллелограмм, называется параллелепипедом.
Параллелепипед, у которого
грани расположены под некоторым углом ≠ 90° к основанию, называется
наклонным.Наклонный параллелепипед
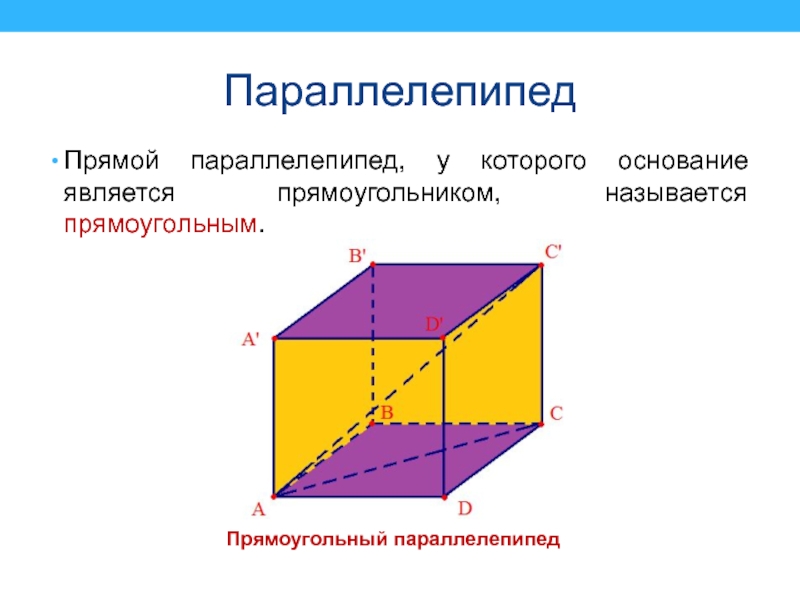
Слайд 32Параллелепипед
Прямой параллелепипед, у которого основание является прямоугольником, называется прямоугольным.
Прямоугольный параллелепипед
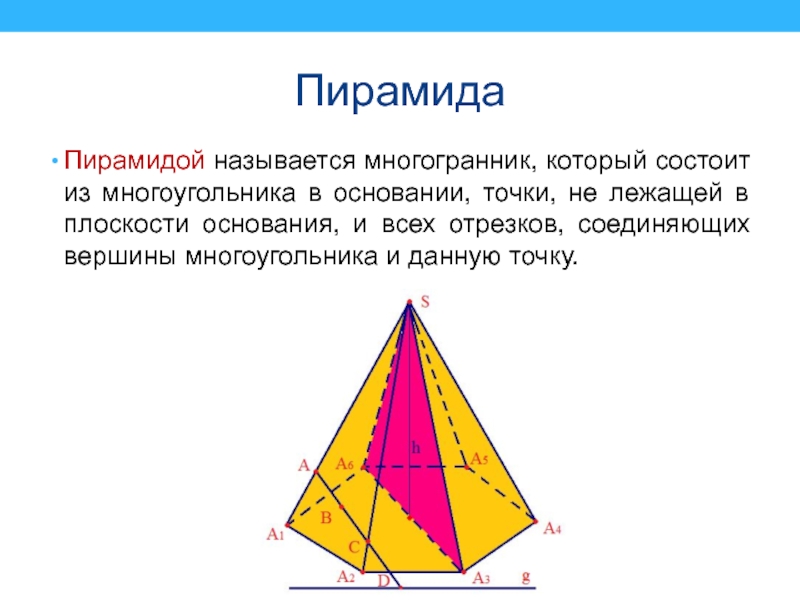
Слайд 33Пирамида
Пирамидой называется многогранник, который состоит из многоугольника в основании, точки,
не лежащей в плоскости основания, и всех отрезков, соединяющих вершины
многоугольника и данную точку.Слайд 34Правильные многогранники
Если выпуклый многогранник имеет все грани правильные многоугольники с
равным числом сторон и в каждой вершине многоугольника сходится одно
и то же число ребер, то такой многогранник называется правильным.Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
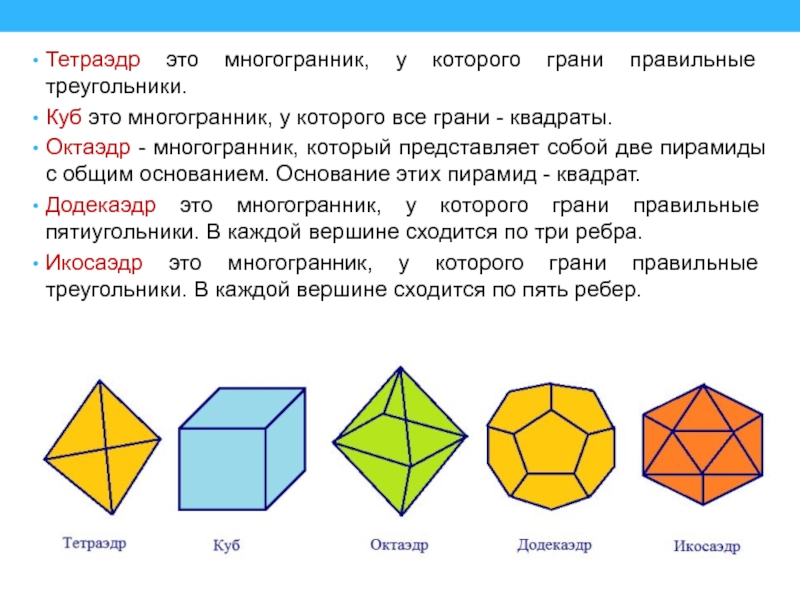
Слайд 35Тетраэдр это многогранник, у которого грани правильные треугольники.
Куб это многогранник,
у которого все грани - квадраты.
Октаэдр - многогранник, который представляет
собой две пирамиды с общим основанием. Основание этих пирамид - квадрат.Додекаэдр это многогранник, у которого грани правильные пятиугольники. В каждой вершине сходится по три ребра.
Икосаэдр это многогранник, у которого грани правильные треугольники. В каждой вершине сходится по пять ребер.
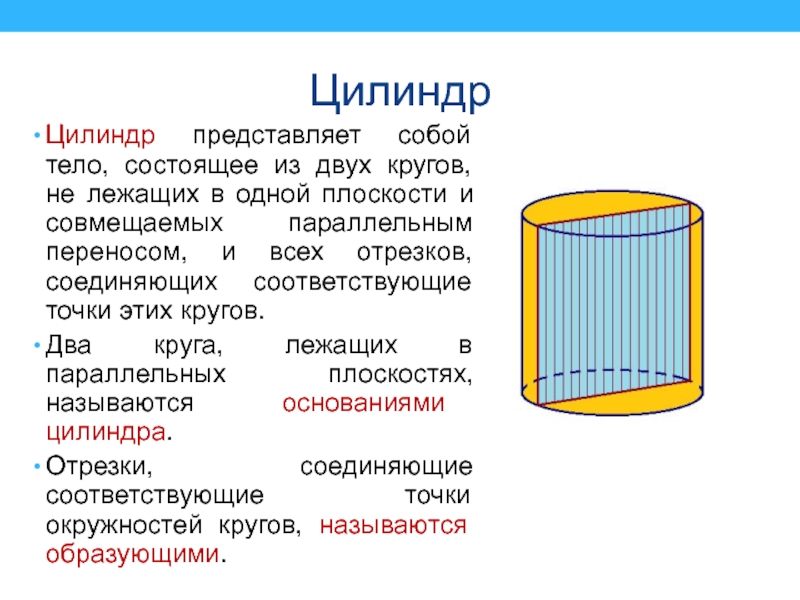
Слайд 36Цилиндр
Цилиндр представляет собой тело, состоящее из двух кругов, не лежащих
в одной плоскости и совмещаемых параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих кругов.Два круга, лежащих в параллельных плоскостях, называются основаниями цилиндра.
Отрезки, соединяющие соответствующие точки окружностей кругов, называются образующими.
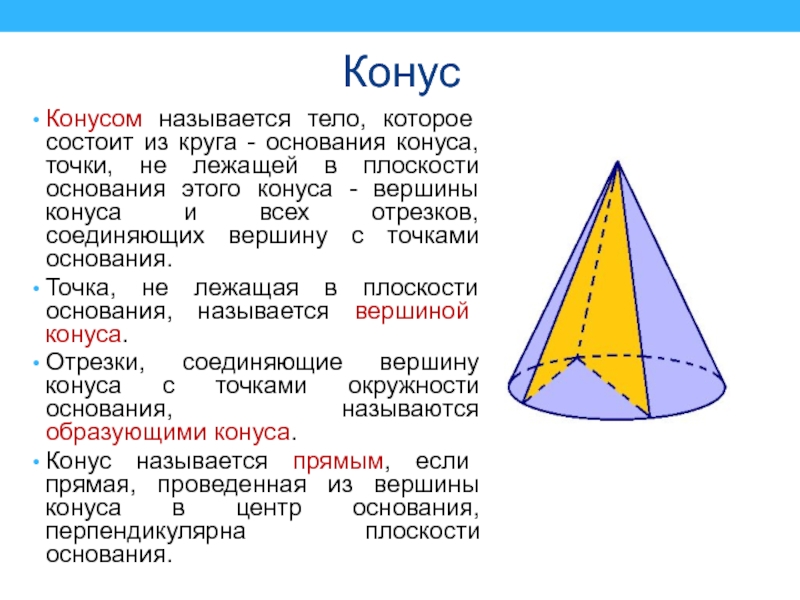
Слайд 37Конус
Конусом называется тело, которое состоит из круга - основания конуса,
точки, не лежащей в плоскости основания этого конуса - вершины
конуса и всех отрезков, соединяющих вершину с точками основания.Точка, не лежащая в плоскости основания, называется вершиной конуса.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус называется прямым, если прямая, проведенная из вершины конуса в центр основания, перпендикулярна плоскости основания.
Слайд 38Шар
Шар это геометрическое тело, состоящее из всех точек пространства, находящихся
на расстоянии, не большем данного, от данной точки.
Точка, от
которой все остальные точки находятся на расстоянии не большем данного, называется центром шара.Граница шара называется сферой. Совокупность всех точек сферы удалена от центра на расстояние, равное радиусу. Таким образом, любой отрезок, соединяющий центр шара с точкой сферы, называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.