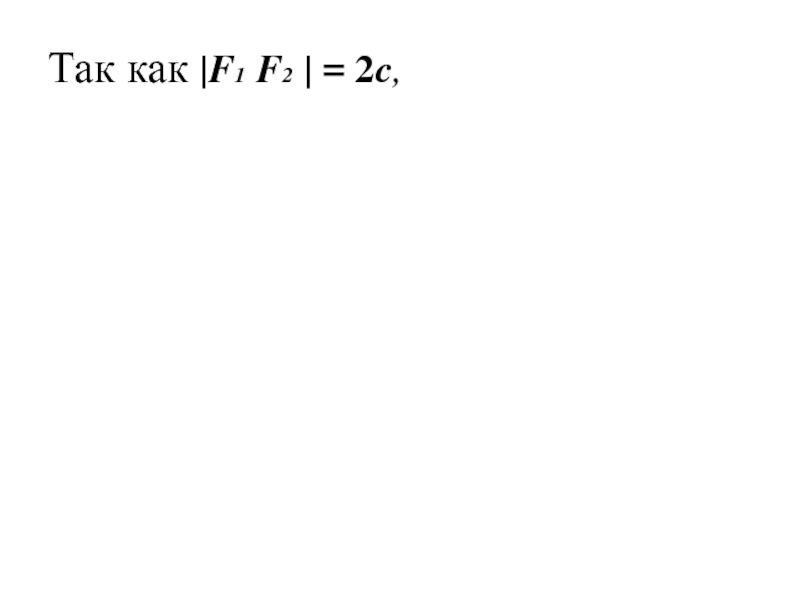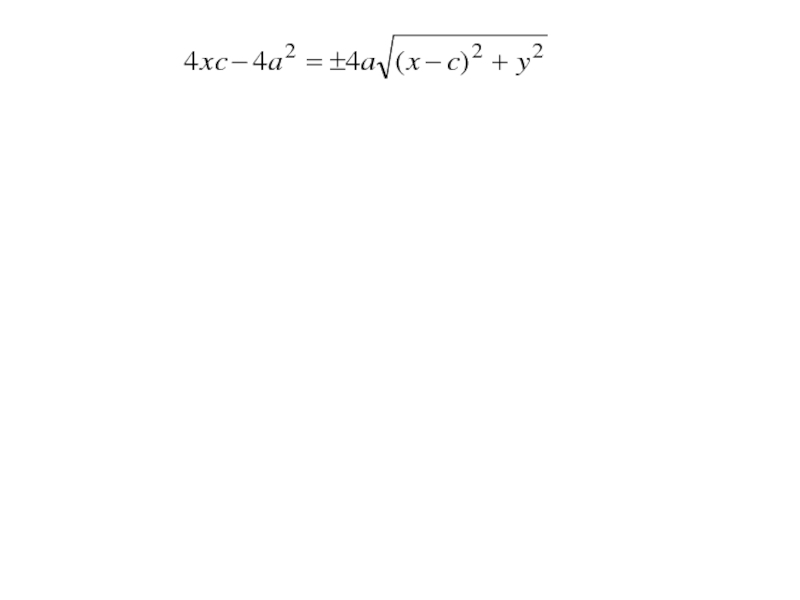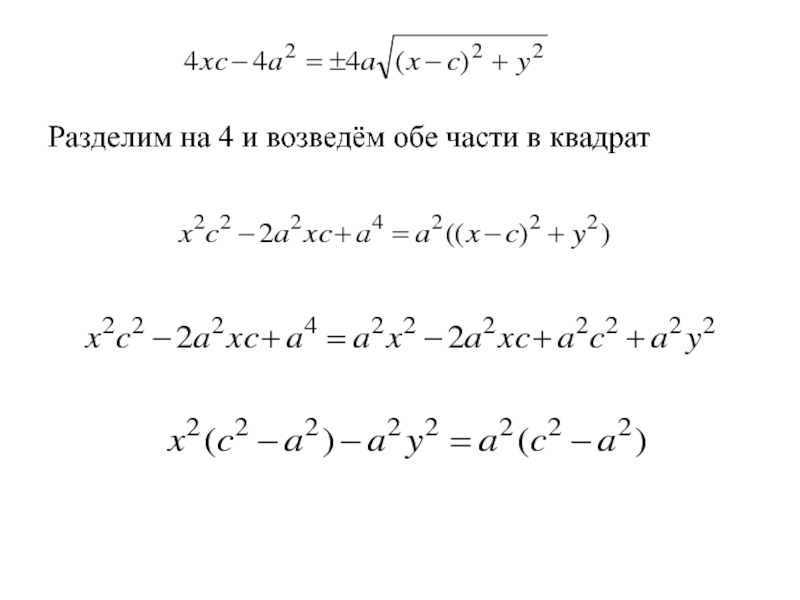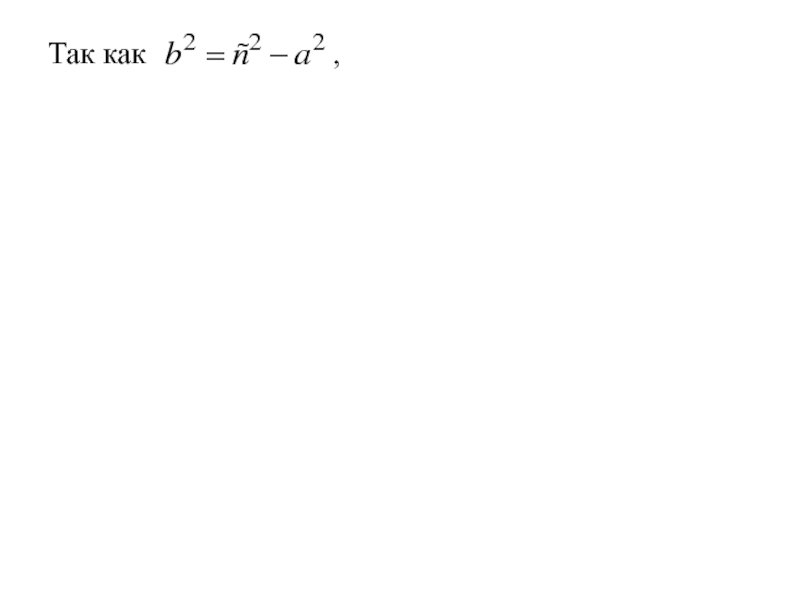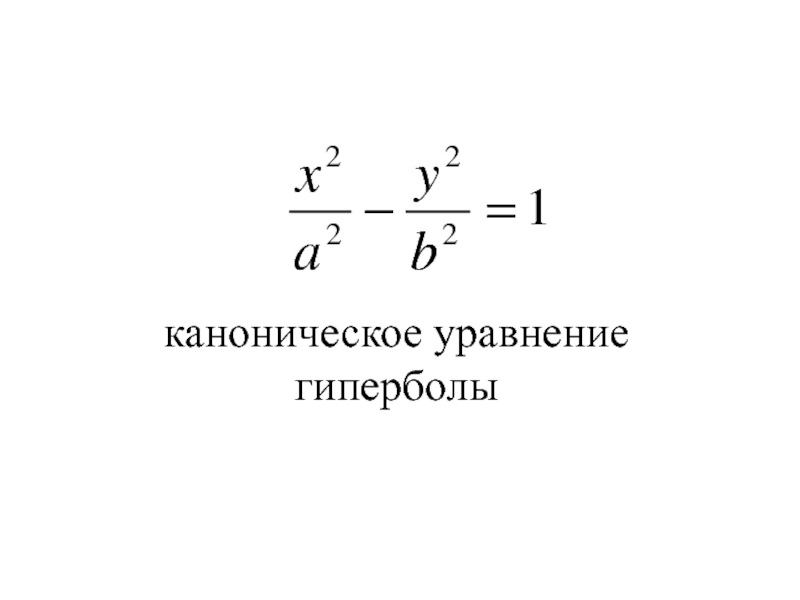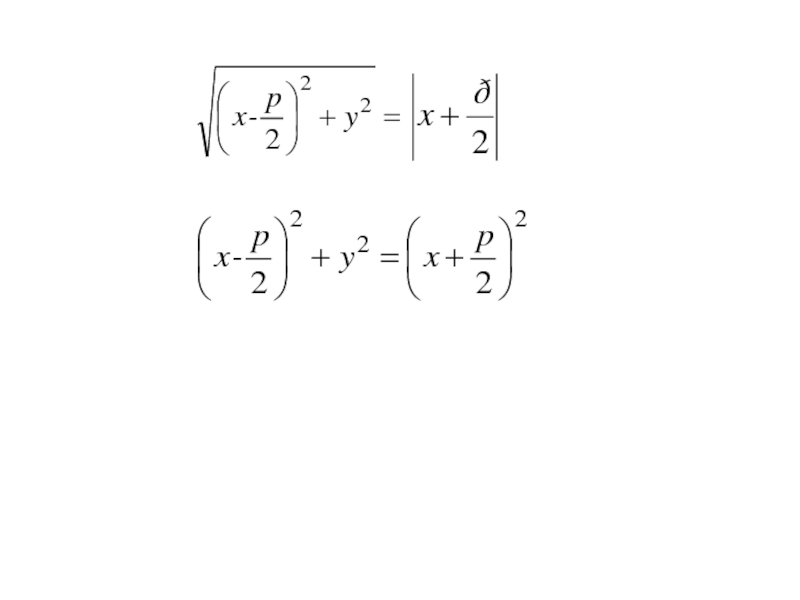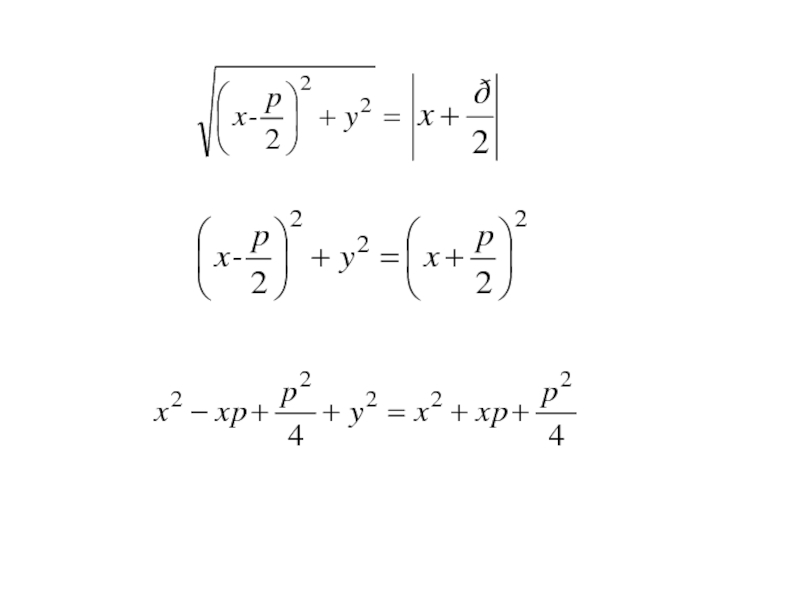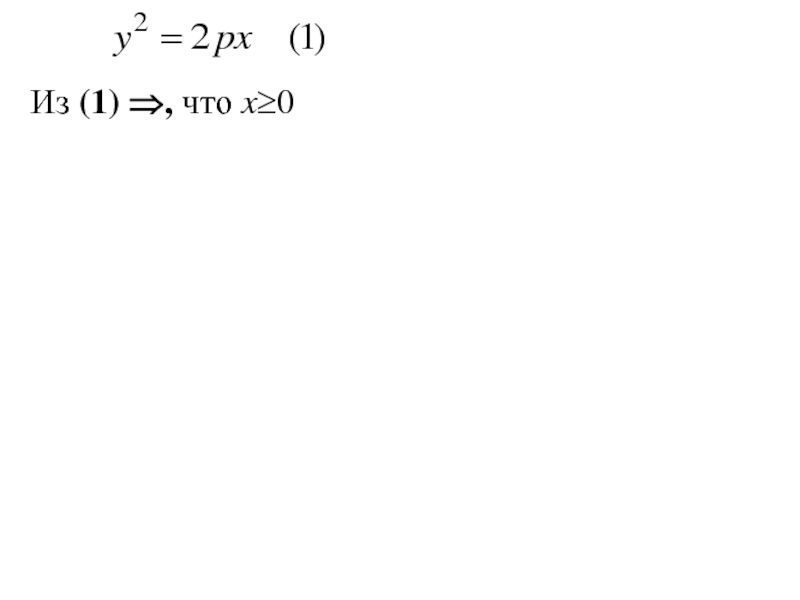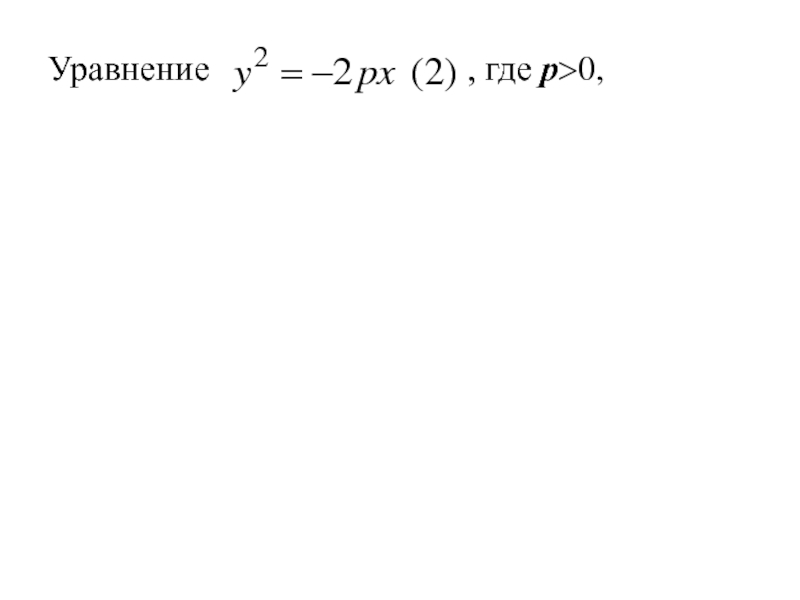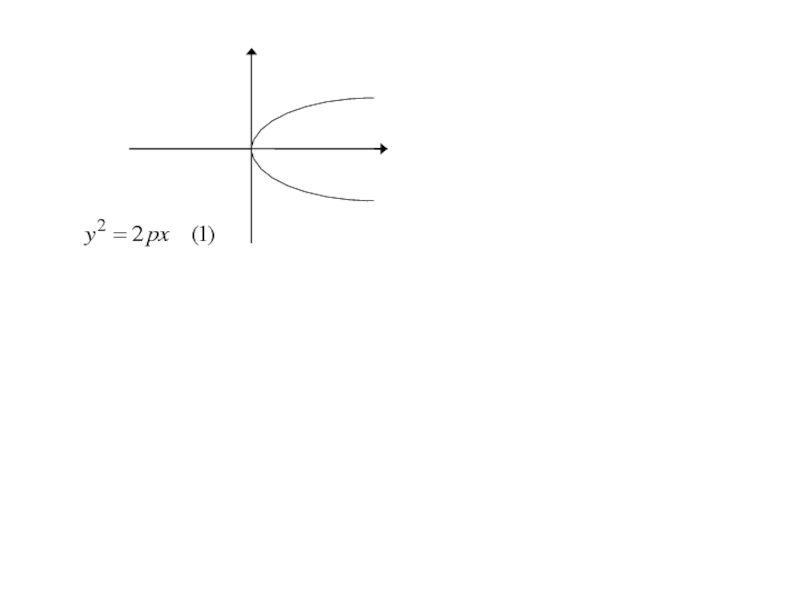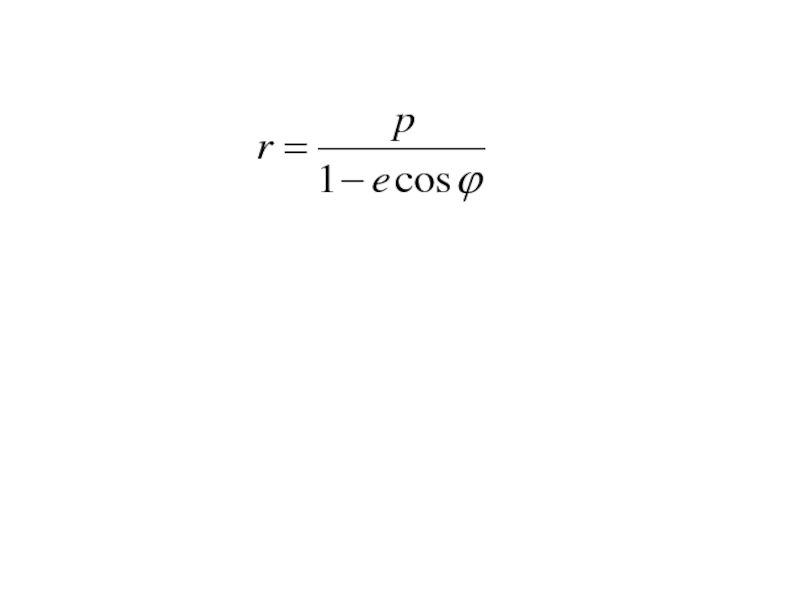Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
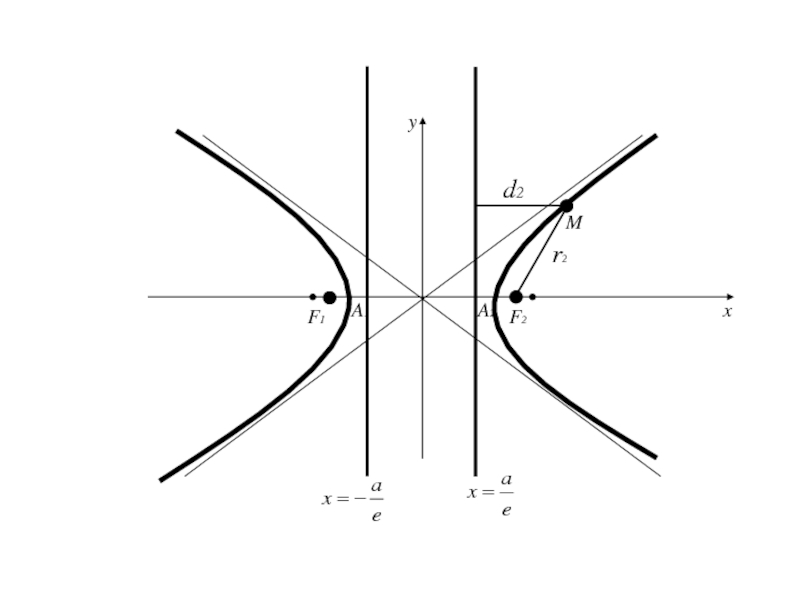
Гипербола и её каноническое уравнение
Содержание
- 1. Гипербола и её каноническое уравнение
- 2. 4. Гипербола и её каноническое уравнение
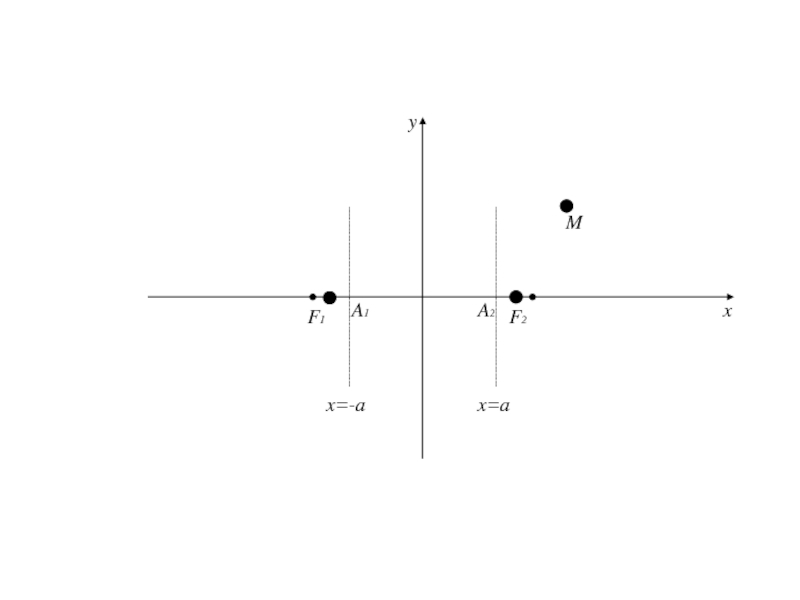
- 3. 4. Гипербола и её каноническое уравнениеГиперболой называется
- 4. M
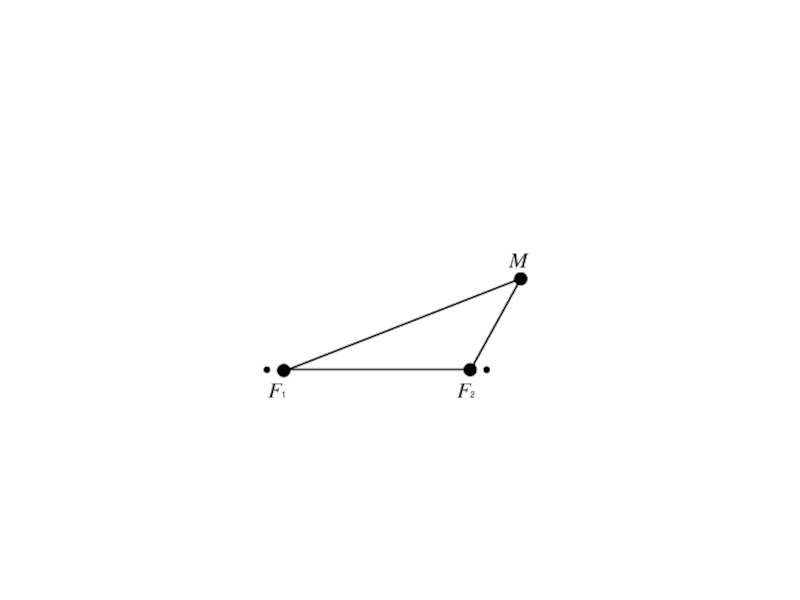
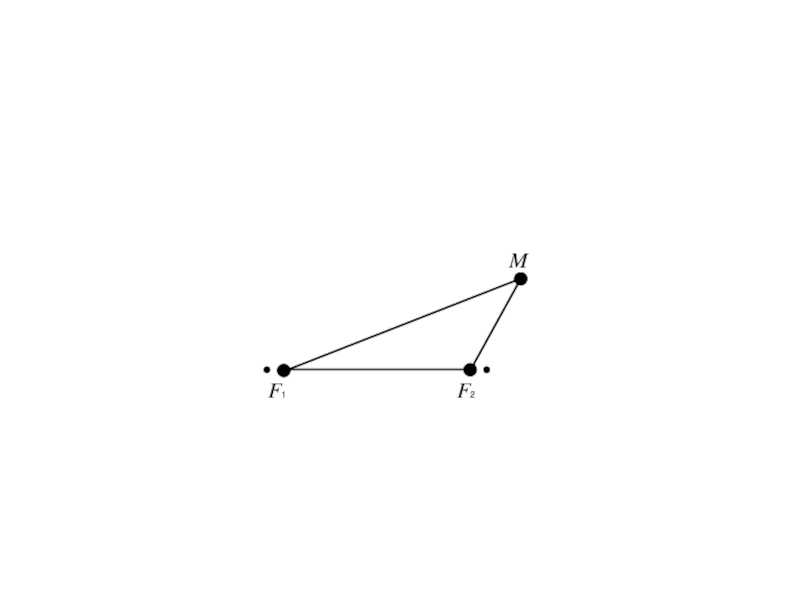
- 5. F1 M
- 6. F1 F2 M
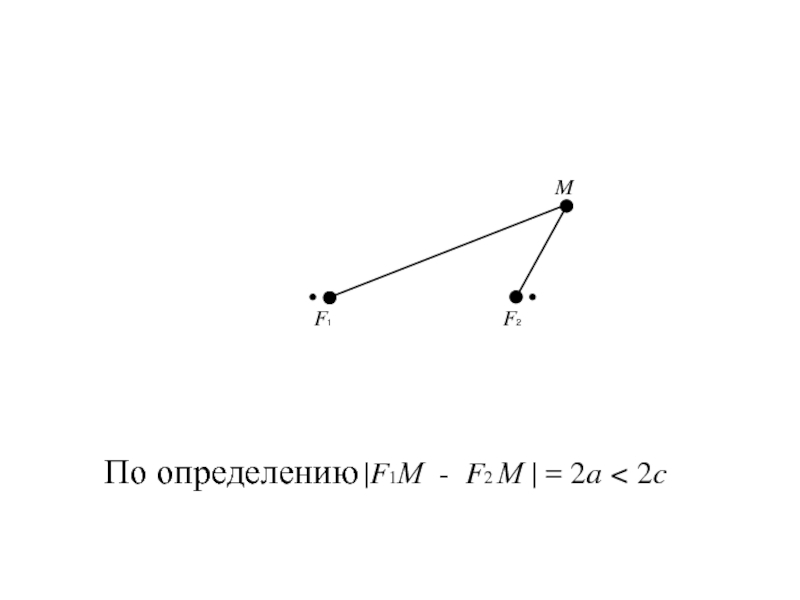
- 7. По определению |F1М - F2 М | = 2a < 2c
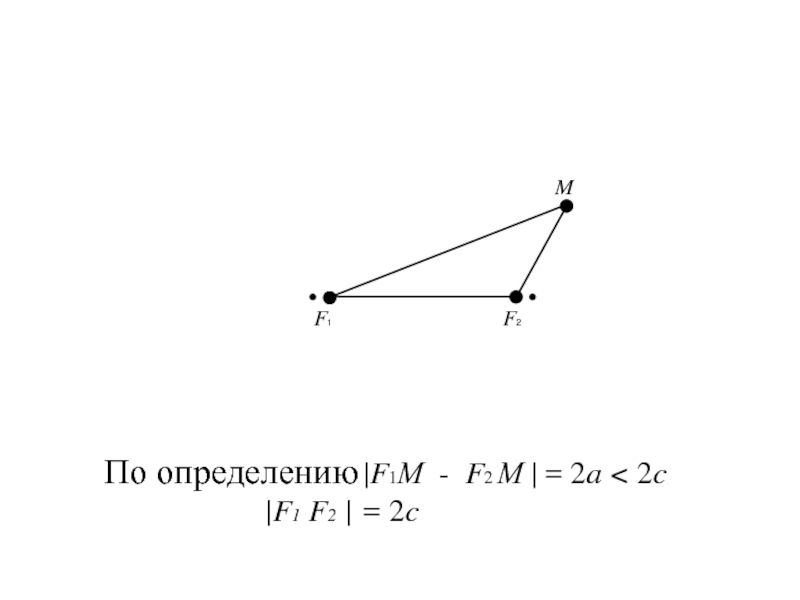
- 8. По определению |F1М - F2 М | = 2a < 2c |F1 F2 | = 2c
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
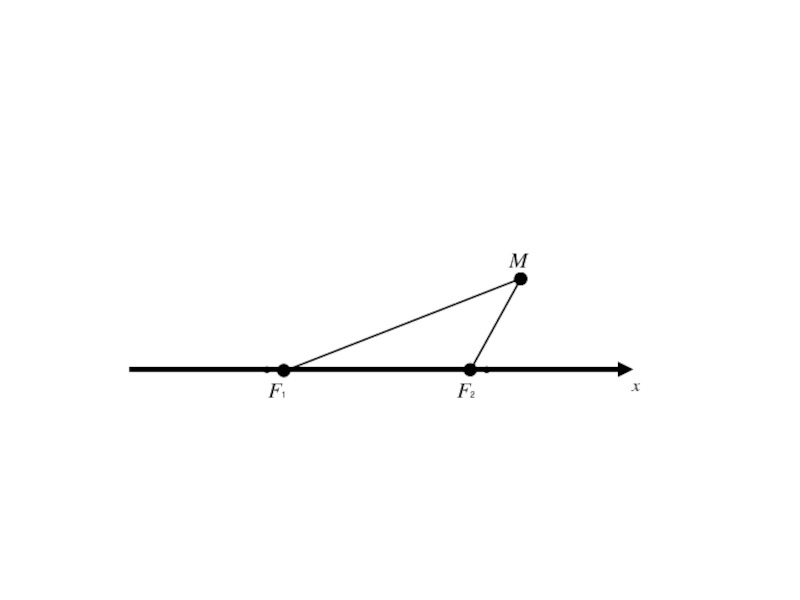
- 12. x
- 13. x
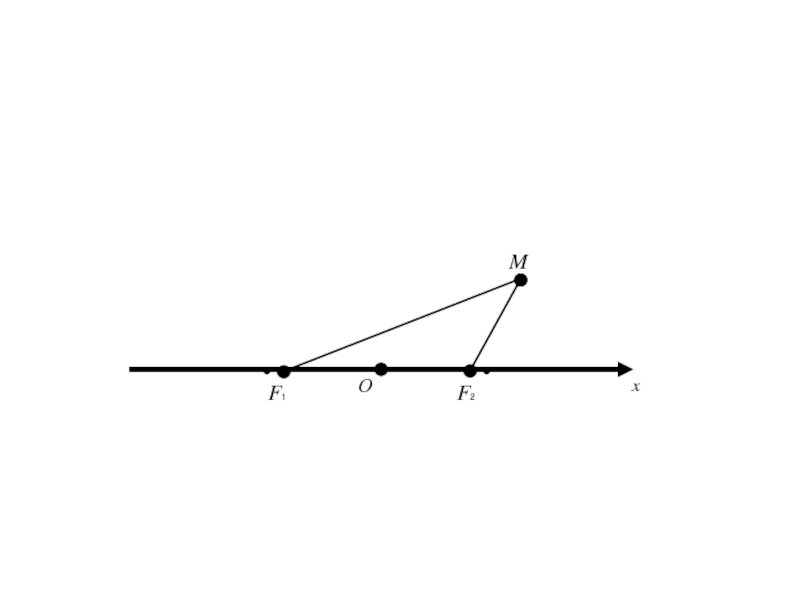
- 14. xF1 F2 MО
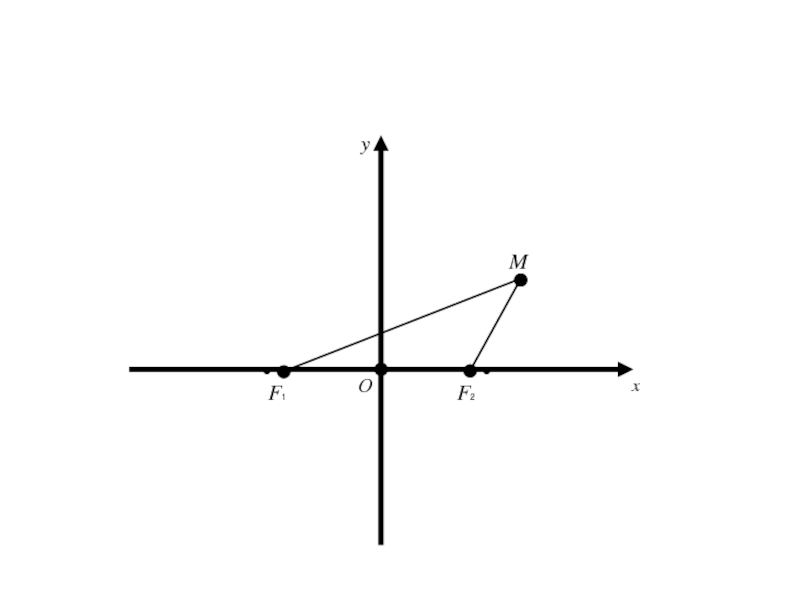
- 15. xF1 F2 MОy
- 16. Так как |F1 F2 | = 2c,
- 17. Так как |F1 F2 | = 2c,
- 18. Так как |F1 F2 | = 2c,
- 19. Так как |F1 F2 | = 2c,
- 20. Так как |F1 F2 | = 2c,
- 21. По определению |F1М - F2 М | = 2a (1)Получим
- 22. По определению |F1М - F2М | = 2a (1) Получим
- 23. По определению |F1М - F2М | =
- 24. По определению |F1М - F2М | =
- 25. По определению |F1М - F2М | =
- 26. По определению |F1М - F2М | =
- 27. По определению |F1М - F2М | =
- 28. Слайд 28
- 29. Разделим на 4 и возведём обе части в квадрат
- 30. Разделим на 4 и возведём обе части в квадрат
- 31. Разделим на 4 и возведём обе части в квадрат
- 32. Разделим на 4 и возведём обе части в квадрат
- 33. Слайд 33
- 34. Так как по определению a < c, обозначим
- 35. Так как по определению a < c, обозначим
- 36. Так как по определению a < c, обозначимполучим выражение
- 37. Так как по определению a < c,
- 38. Так как по определению a < c,
- 39. Мы доказали, что координаты любой точки гиперболы удовлетворяют уравнению (2)
- 40. Докажем обратное: если координаты некоторой точки М(x,y)
- 41. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 42. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 43. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 44. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 45. Так как ,
- 46. Так как , значит
- 47. Так как
- 48. Так как
- 49. Так как
- 50. Так как
- 51. Отрезки F1M и F2M назовем фокальными радиусами гиперболы
- 52. Отрезки F1M и F2M назовем фокальными радиусами гиперболы
- 53. Отрезки F1M и F2M назовем фокальными радиусами
- 54. Отрезки F1M и F2M назовем фокальными радиусами
- 55. Отрезки F1M и F2M назовем фокальными радиусами
- 56. Отрезки F1M и F2M назовем фокальными радиусами
- 57. Отрезки F1M и F2M назовем фокальными радиусами
- 58. Отрезки F1M и F2M назовем фокальными радиусами
- 59. Отрезки F1M и F2M назовем фокальными радиусами
- 60. Таким образом, получаем если
- 61. Таким образом, получаем если
- 62. Таким образом, получаем если
- 63. Таким образом, получаем если
- 64. Таким образом, получаем если
- 65. Таким образом, получаем если
- 66. Таким образом, получаем если
- 67. Таким образом, получаем если
- 68. Таким образом, уравнение (2) есть уравнение гиперболы,
- 69. каноническое уравнение гиперболы
- 70. каноническое уравнение гиперболы
- 71. 5. Исследование формы гиперболы
- 72. 5. Исследование формы гиперболыТ.к. в каноническое уравнение гиперболы координаты x и y входят во второй степени
- 73. 5. Исследование формы гиперболыТ.к. в каноническое уравнение
- 74. Из уравнения => что
- 75. Из уравнения => что
- 76. Ось симметрии Ox пересекает гиперболу в двух
- 77. Ось симметрии Ox пересекает гиперболу в двух
- 78. Выразим y из уравнения гиперболы и возьмем положительное значение
- 79. Выразим y из уравнения гиперболы и возьмем
- 80. Выразим y из уравнения гиперболы и возьмем
- 81. Выразим y из уравнения гиперболы и возьмем
- 82. Выразим y из уравнения гиперболы и возьмем
- 83. Всякая прямая пересекает гиперболу не более чем
- 84. Рассмотрим уравнение прямой
- 85. Рассмотрим уравнение прямой
- 86. Рассмотрим уравнение прямой
- 87. Рассмотрим уравнение прямой
- 88. Рассмотрим уравнение прямой
- 89. Получили, что на полуинтервале
- 90. Получили, что на полуинтервале
- 91. xy
- 92. xy
- 93. xyM
- 94. xyMd
- 95. xyMd
- 96. В силу того, что гипербола, заданная каноническим
- 97. Так как гипербола, заданная каноническим уравнением, симметрична
- 98. x=-aA1A2F1F2Mxyx=a
- 99. PQSKA1A2F1F2Mxyx=-ax=ay=-by=b
- 100. PQSKA1A2F1F2Mxy
- 101. PQSKA1A2F1F2Mxy
- 102. PQSKA1A2F1F2Mxy
- 103. PQSKA1A2F1F2Mxy
- 104. A1A2F1F2Mxy
- 105. Гипербола, у которой полуоси равны, называется равностороннейУравнения её асимптот
- 106. 6. Эксцентриситет и директрисы гиперболы
- 107. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 108. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 109. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 110. Перепишем формулы для фокальных радиусов если
- 111. Перепишем формулы для фокальных радиусов если
- 112. Две прямые, перпендикулярные действительной оси гиперболы и
- 113. Для гиперболы, заданной каноническим уравнениемуравнения директрис имеют вид
- 114. Для гиперболы, заданной каноническим уравнениемуравнения директрис имеют
- 115. A1A2F1F2Mxy
- 116. A1A2F1F2Mxy
- 117. Теорема: Для того чтобы точка лежала на
- 118. A1A2F1F2Mxyr2
- 119. A1A2F1F2Mxyr2d2
- 120. A1A2F1F2Mxyr2d2 125
- 121. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняется
- 122. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняется
- 123. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняетсятребуется доказать, что
- 124. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняетсятребуется доказать, что Найдём
- 125. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняетсятребуется доказать, что найдём
- 126. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняетсятребуется доказать, что найдём
- 127. Пусть существует точка
- 128. Пусть существует точка
- 129. Пусть существует точка
- 130. Пусть существует точка
- 131. Пусть существует точка
- 132. Пусть существует точка
- 133. Самостоятельно изучить вопросы по данной теме:Понятие сопряженной гиперболыУравнение касательной к гиперболеОптическое свойство гиперболы
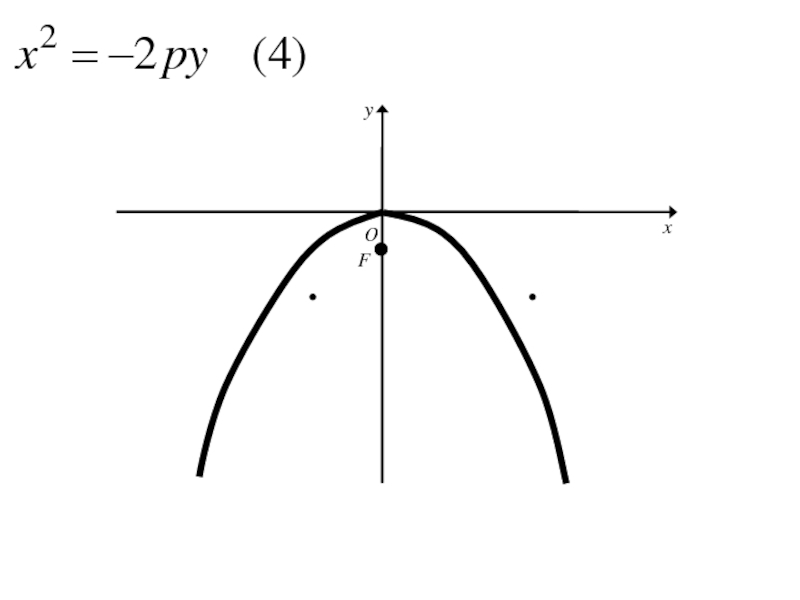
- 134. 7. Парабола и её каноническое уравнение
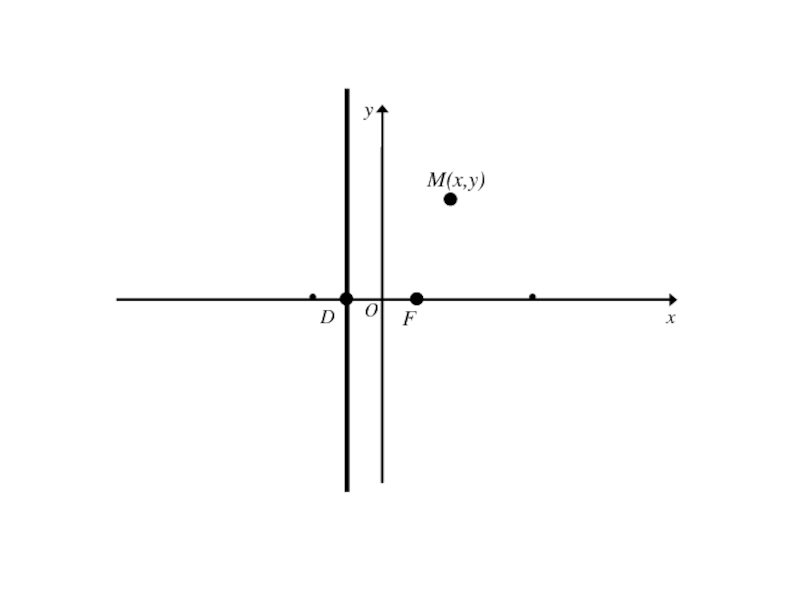
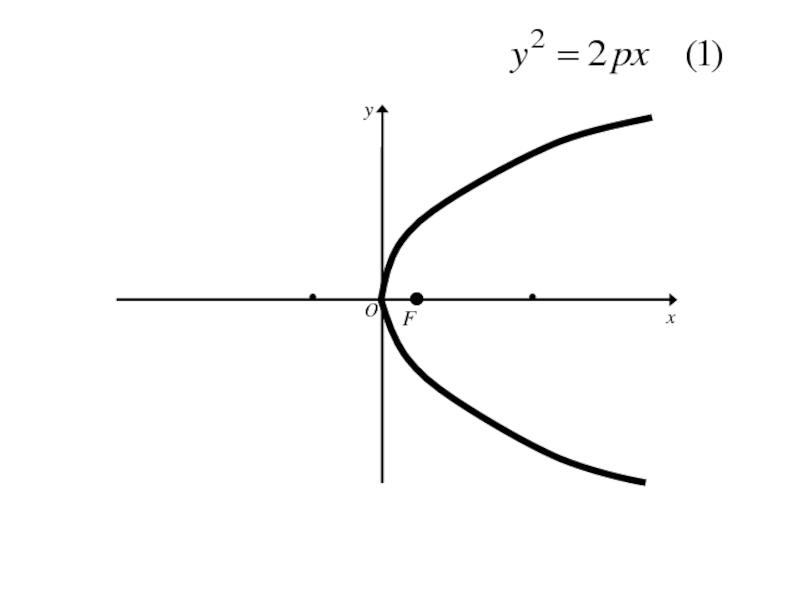
- 135. 7. Парабола и её каноническое уравнение Параболой
- 136. 7. Парабола и её каноническое уравнение Расстояние от фокуса параболы до её директрисы называется параметром параболы.
- 137. 7. Парабола и её каноническое уравнение Расстояние
- 138. F
- 139. F
- 140. F
- 141. FD
- 142. FDO
- 143. FDOx
- 144. FDOxy
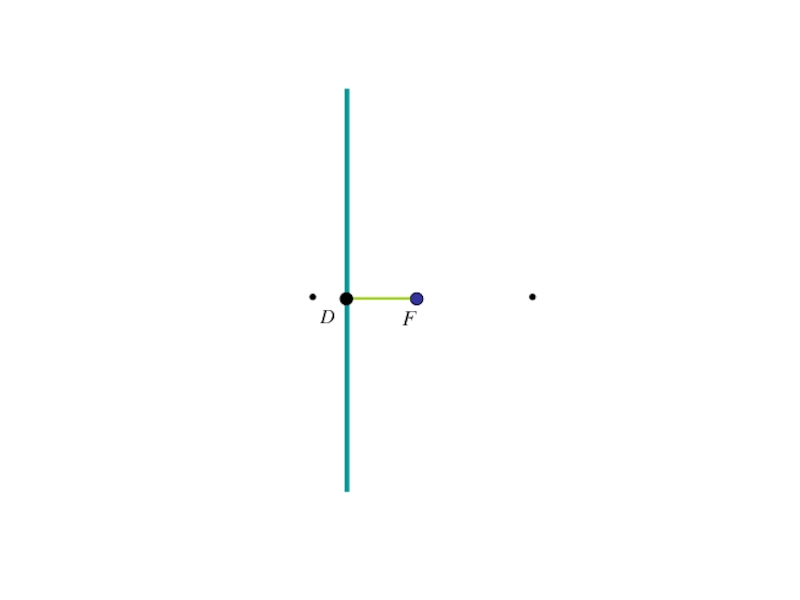
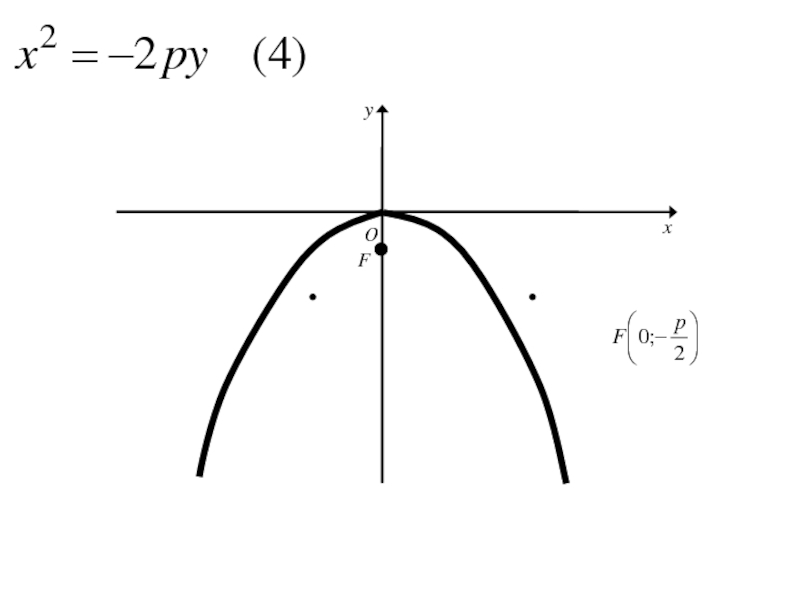
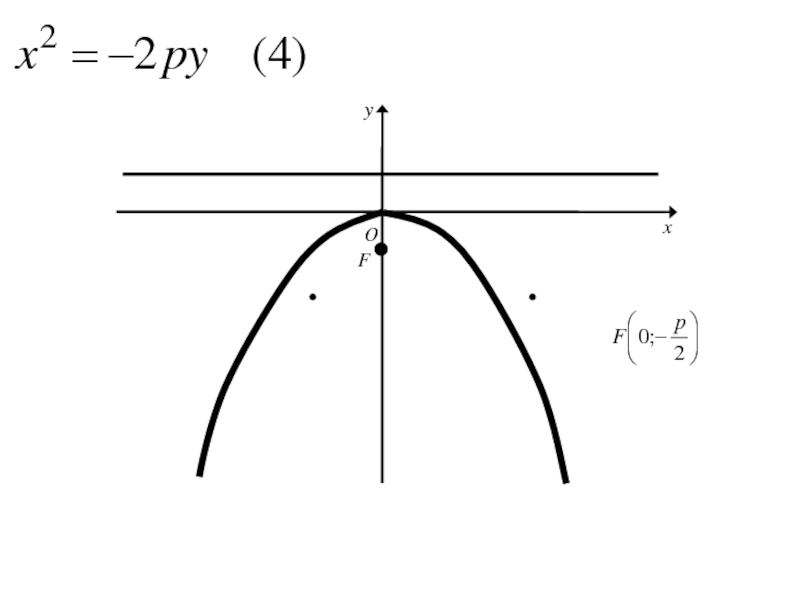
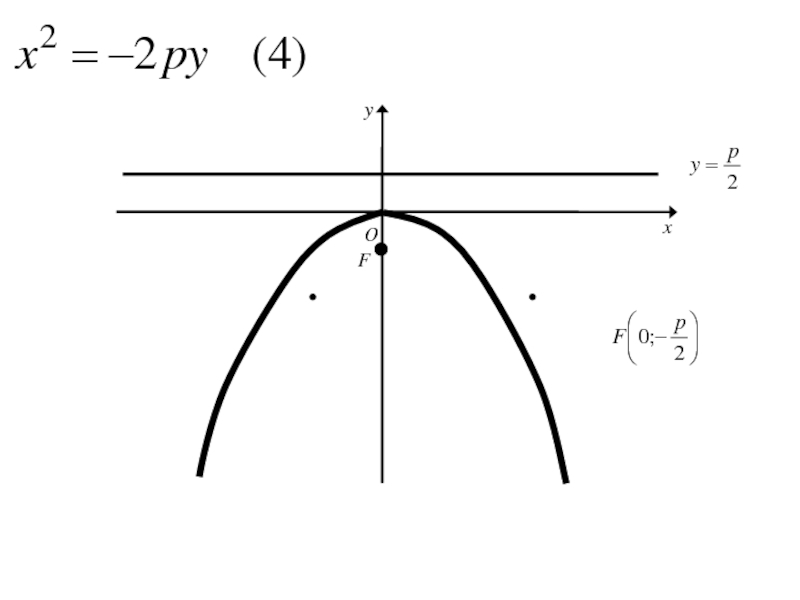
- 145. Расстояние FD обозначим р (параметр параболы).
- 146. Расстояние FD обозначим р (параметр параболы).тогда в выбранной системе координат фокус F будет иметь координаты
- 147. Расстояние FD обозначим р (параметр параболы).тогда в
- 148. Расстояние FD обозначим р (параметр параболы).тогда в
- 149. Расстояние FD обозначим р (параметр параболы).тогда в
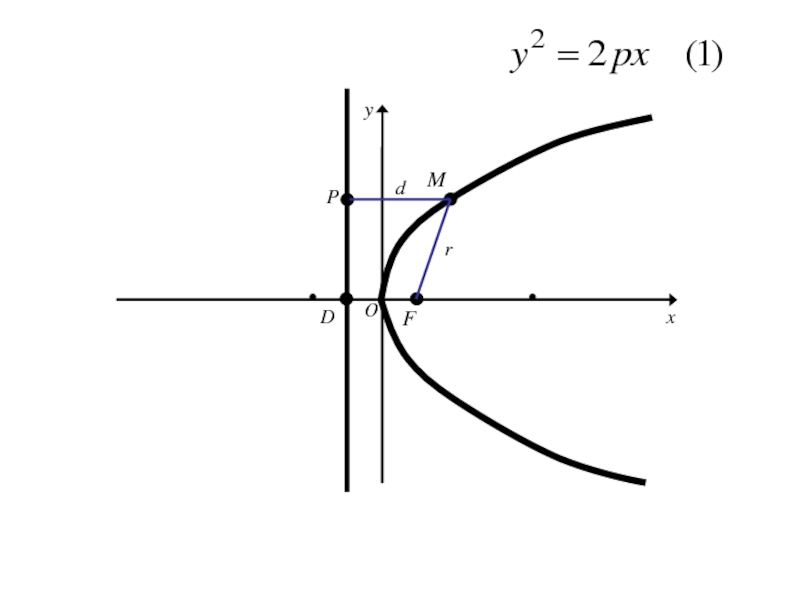
- 150. M(x,y)FDOxy
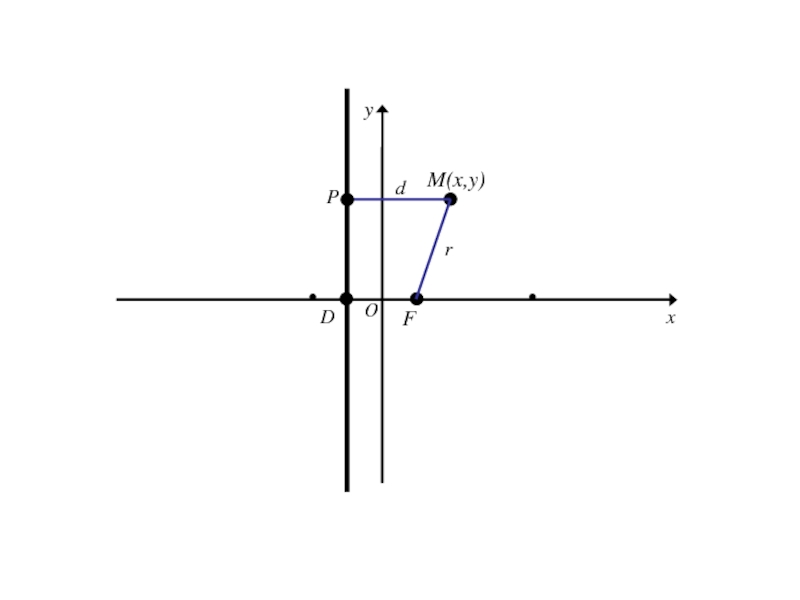
- 151. M(x,y)FDOxyr
- 152. M(x,y)FDOxyrPd
- 153. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d
- 154. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|=
- 155. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|=
- 156. Точка M(x;y) лежит на данной параболе тогда
- 157. Точка M(x;y) лежит на данной параболе тогда
- 158. Точка M(x;y) лежит на данной параболе тогда
- 159. Слайд 159
- 160. Слайд 160
- 161. Слайд 161
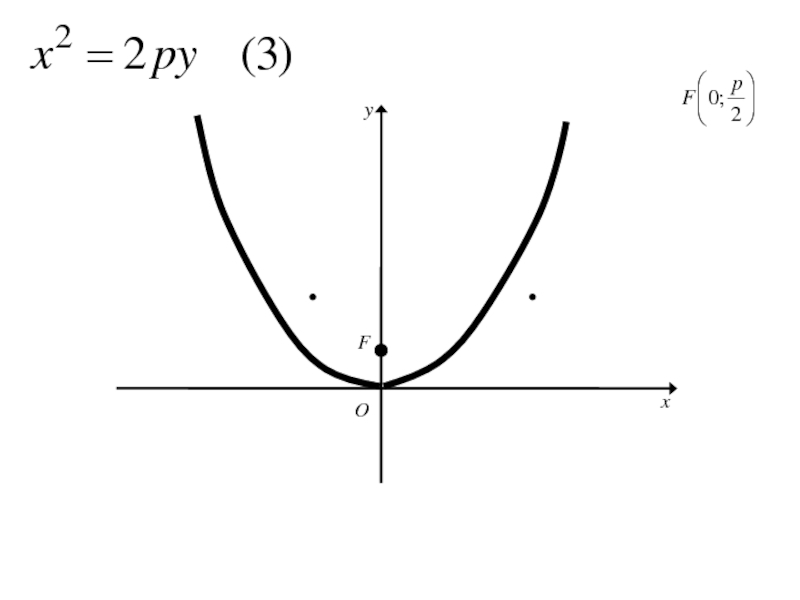
- 162. Каноническое уравнение параболы
- 163. Каноническое уравнение параболы
- 164. 8. Исследование формы параболы
- 165. 8. Исследование формы параболыТ.к. ордината у в каноническом уравнении параболы входит во 2-й степени, то
- 166. 8. Исследование формы параболыТ.к. ордината у в
- 167. 8. Исследование формы параболыТ.к. ордината у в
- 168. 8. Исследование формы параболыТ.к. ордината у в
- 169. 8. Исследование формы параболыТ.к. ордината у в
- 170. 8. Исследование формы параболыВсякая прямая пересекает параболу не более чем в двух точках
- 171. 8. Исследование формы параболыВсякая прямая пересекает параболу
- 172. Из (1) ⇒, что x≥0
- 173. Из (1) ⇒, что x≥0 (т. к. p>0, а
- 174. Из (1) ⇒, что x≥0 (т. к.
- 175. Из (1) ⇒, что x≥0 (т. к.
- 176. Из (1) ⇒, что x≥0 (т. к.
- 177. Из (1) ⇒, что x≥0 (т. к.
- 178. Из (1) ⇒, что x≥0 (т. к.
- 179. MFDOxyPrd
- 180. MFDOxyPrd
- 181. MFDOxyPrd
- 182. Уравнение
- 183. Уравнение
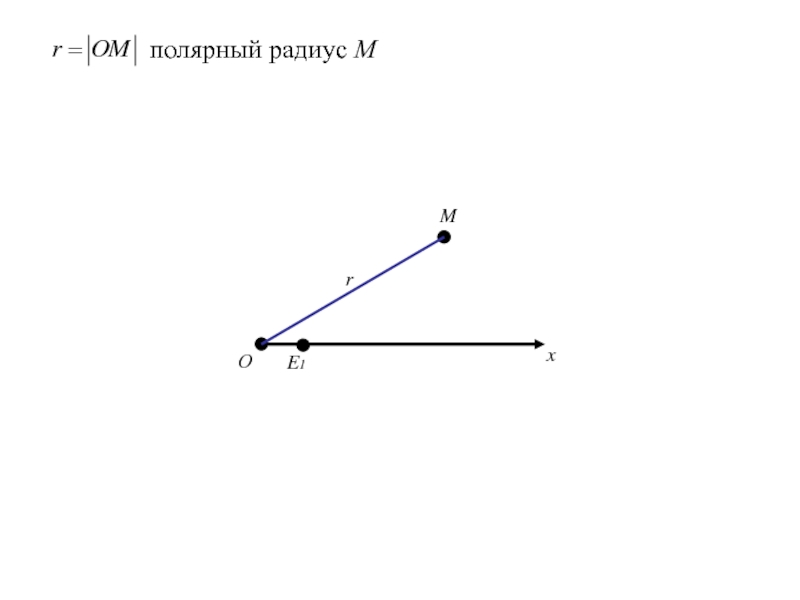
- 184. Уравнение
- 185. Уравнение
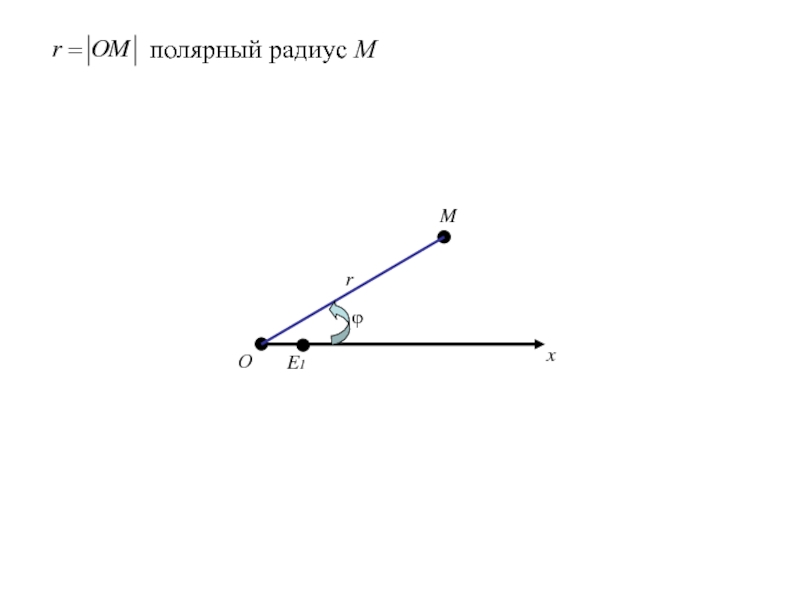
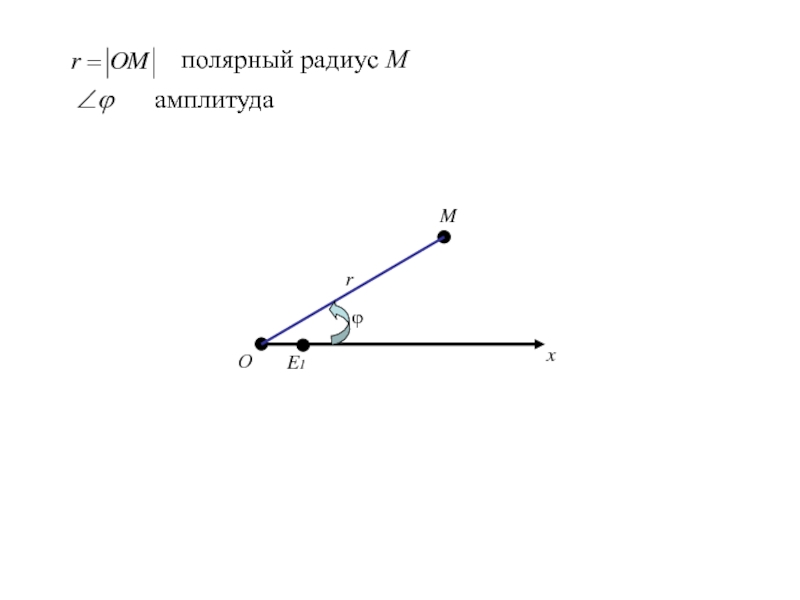
- 186. FOxy
- 187. FOxy
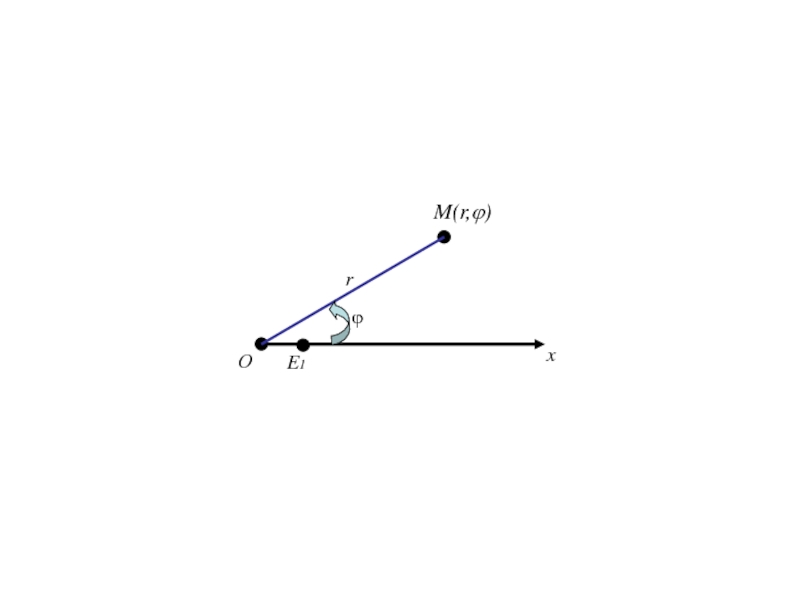
- 188. FOxy
- 189. Oxy
- 190. FOxy
- 191. FOxy
- 192. FOxy
- 193. FOxy
- 194. Аналогичными рассуждениями устанавливаем, что каждое из уравнений
- 195. Oxy
- 196. FOxy
- 197. FOxy
- 198. FOxy
- 199. FOxy
- 200. Oxy
- 201. OxyF
- 202. OxyF
- 203. OxyF
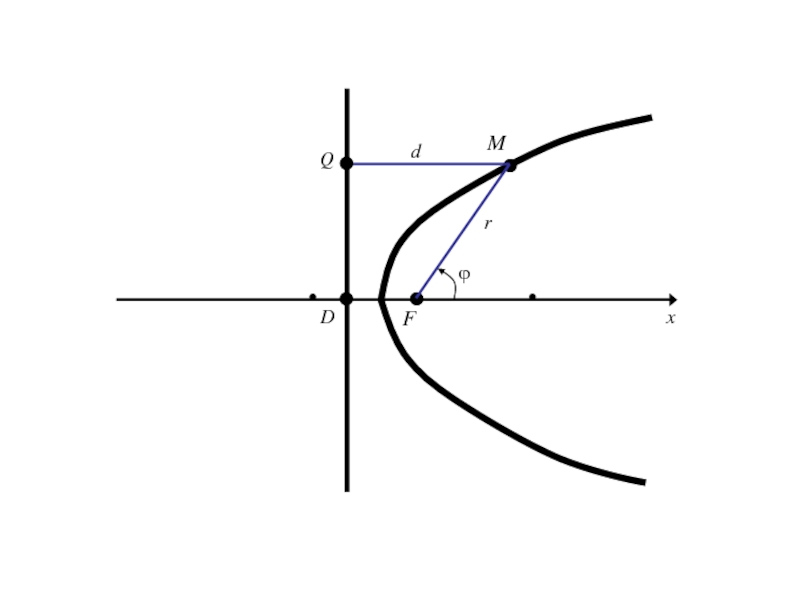
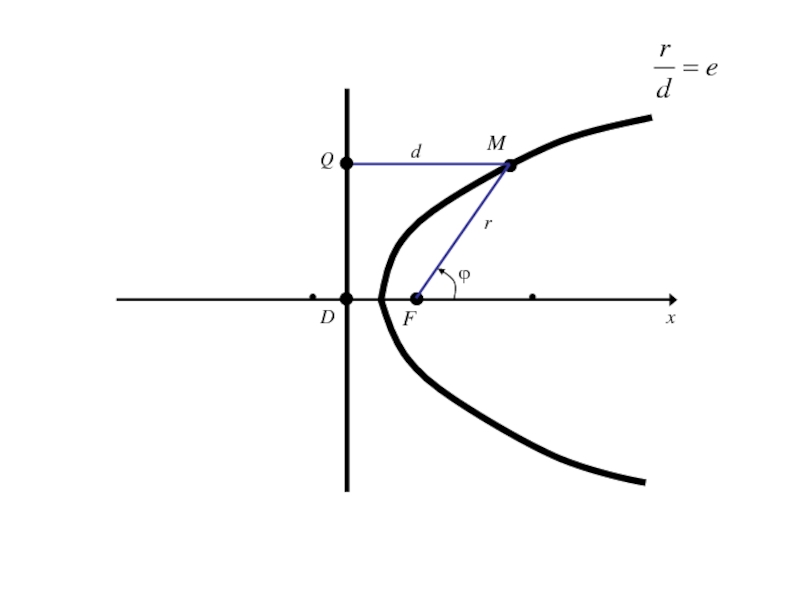
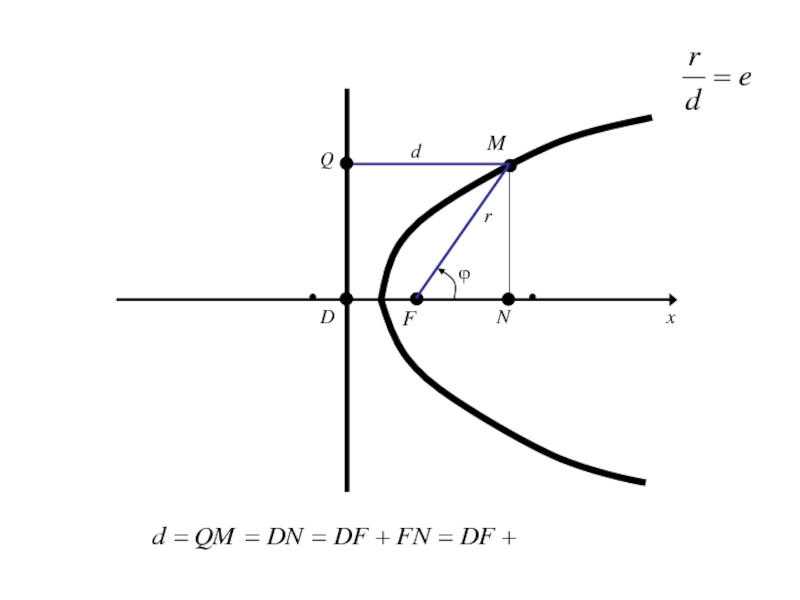
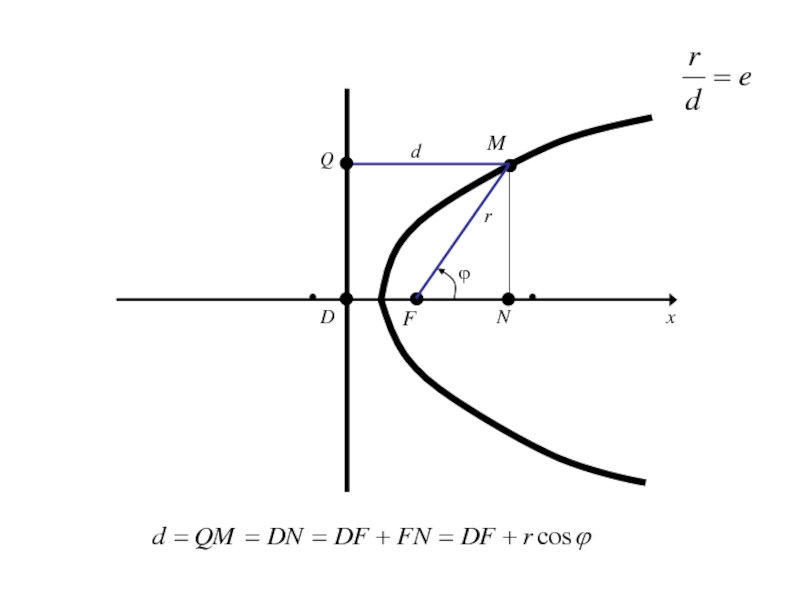
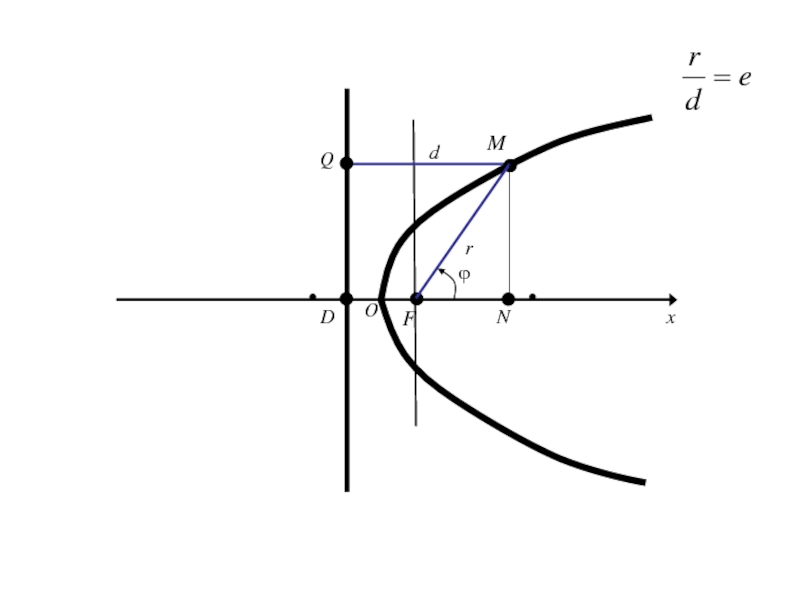
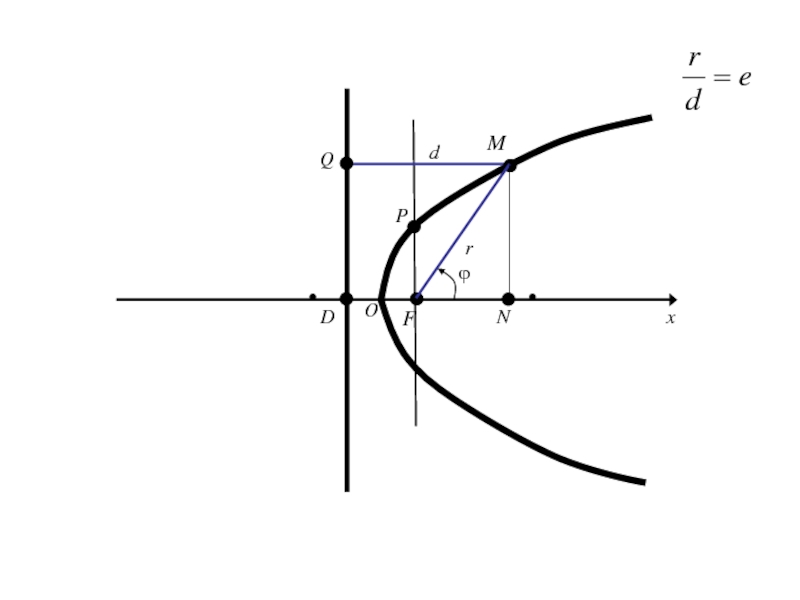
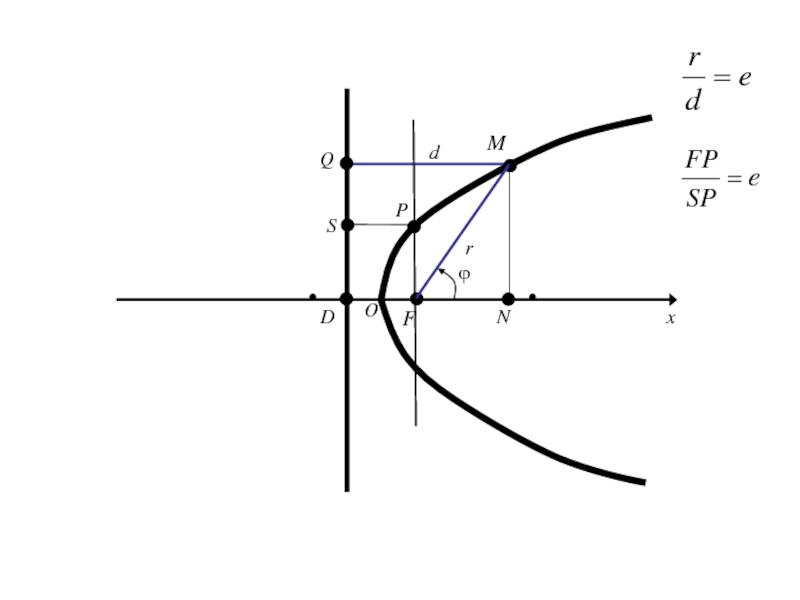
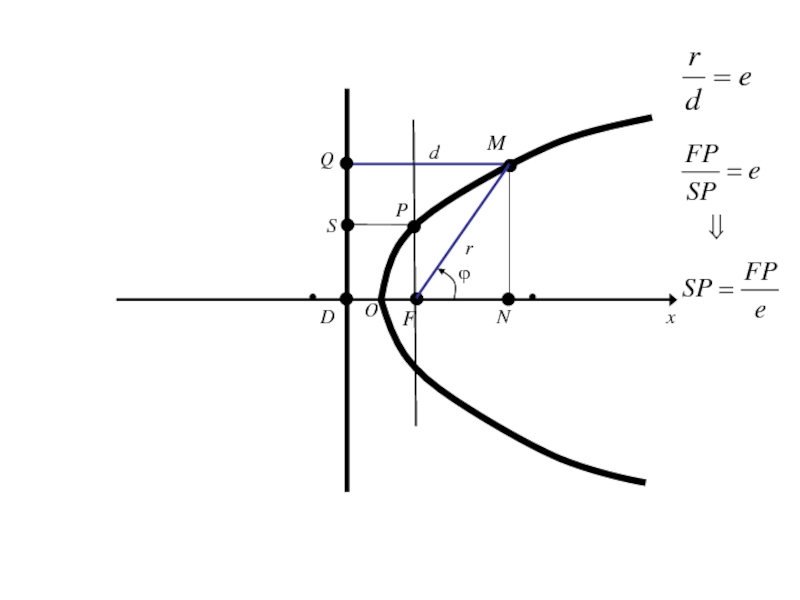
- 204. OxyF
- 205. Слайд 205
- 206. Слайд 206
- 207. Слайд 207
- 208. Слайд 208
- 209. Самостоятельно изучить вопросы по данной теме:Уравнение касательной к параболеОптическое свойство параболы
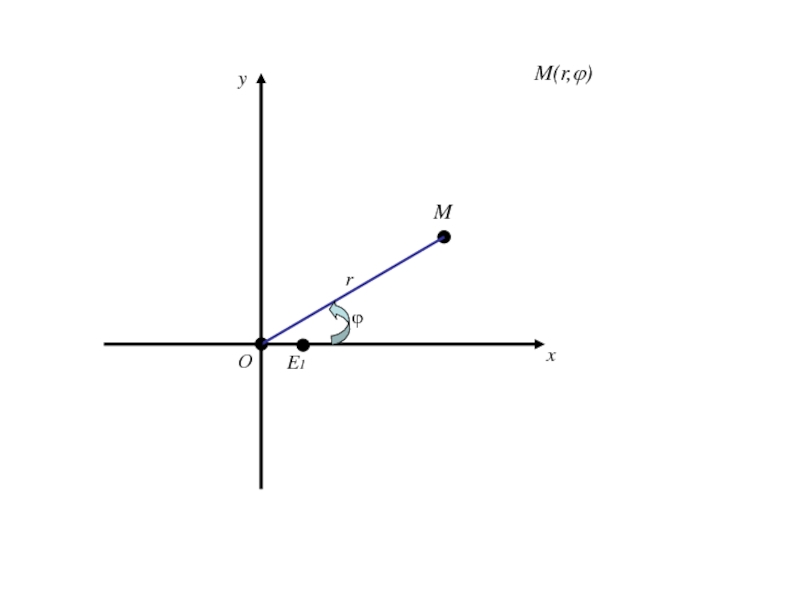
- 210. 9.Уравнение эллипса, параболы и гиперболы в полярных координатах.
- 211. Полярная система координат на плоскости. Говорят, что
- 212. О
- 213. Оx
- 214. ОxE1
- 215. ОxE1M
- 216. ОxE1Mr
- 217. ОxE1Mrполярный радиус М
- 218. ОxE1Mrполярный радиус Мϕ
- 219. ОxE1Mr
- 220. ОxE1r ϕM(r,ϕ)
- 221. ОxE1r Введём ДПСК ϕM
- 222. ОxE1r ϕM
- 223. ОxE1r ϕMy
- 224. ОxE1r ϕMyM(r,ϕ)
- 225. ОxE1r ϕMyM(x,y)M(r,ϕ)
- 226. ОxE1r ϕMyM(x,y)M(r,ϕ)K
- 227. ОxE1r ϕMyM(x,y)M(r,ϕ)K
- 228. ОxE1r ϕMyM(x,y)M(r,ϕ)K
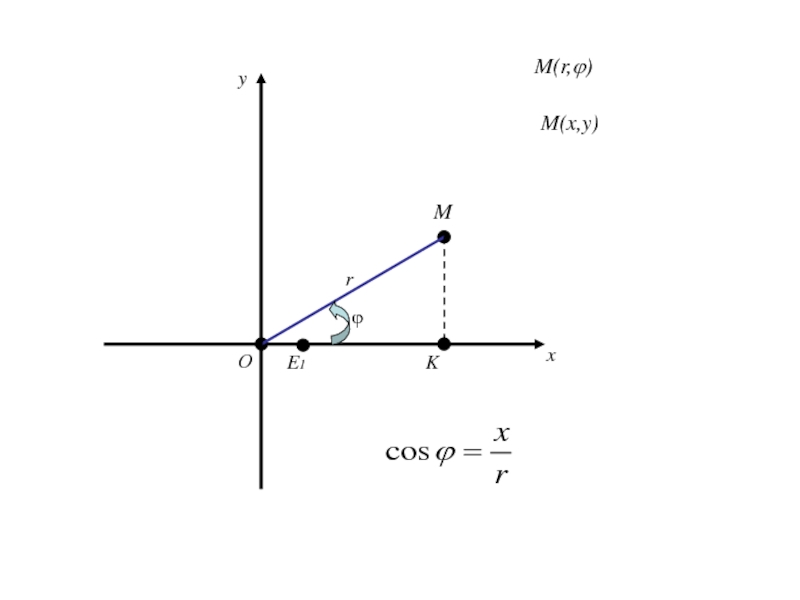
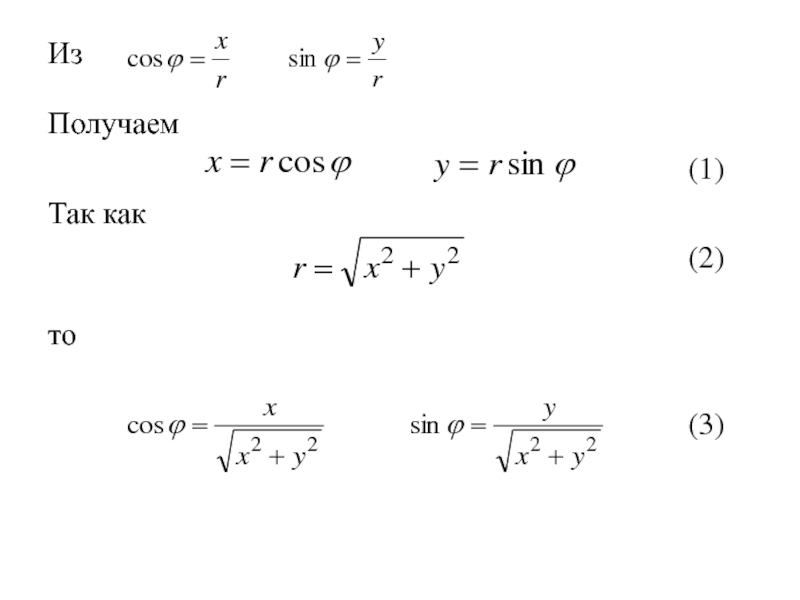
- 229. Из Получаем (1)
- 230. Из Получаем (1)Так как (2)
- 231. Из Получаем (1)Так как (2)то (3)
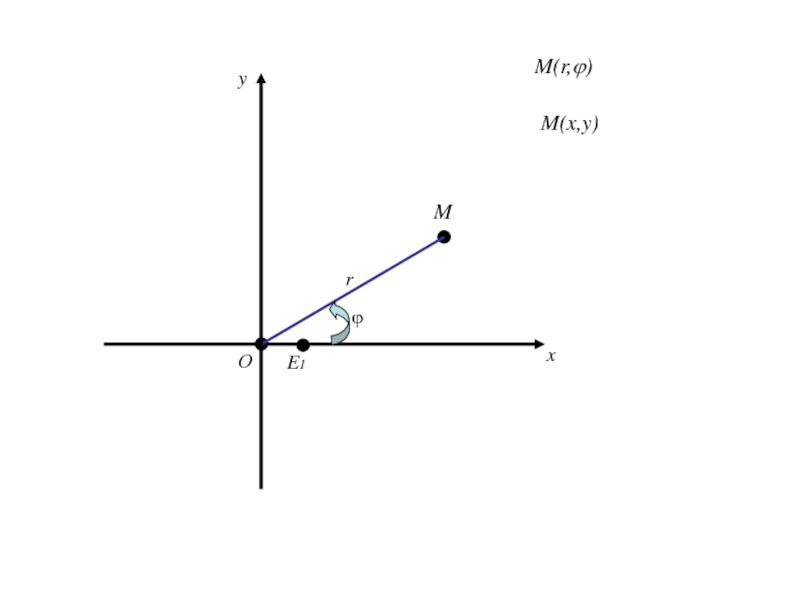
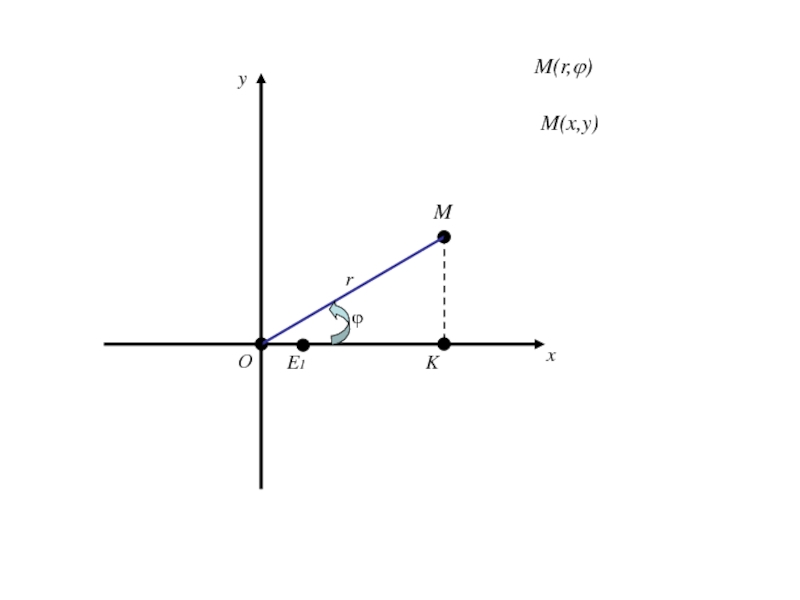
- 232. Формулы (1) позволяют вычислить декартовые прямоугольные координаты х, у точки М по её полярным координатам ϕ,r.
- 233. Формулы (1) позволяют вычислить декартовые прямоугольные координаты
- 234. Полярное уравнение эллипса, гиперболы и параболы Пусть
- 235. Полярное уравнение эллипса, гиперболы и параболы Пусть
- 236. Введем полярную систему координат, совмещая полюс с
- 237. Пусть D-основание перпендикуляра, опущенного из F на
- 238. MFDx
- 239. MFDxrϕ
- 240. MFDxrdQϕ
- 241. MFDxrdQϕ
- 242. MFDxrdQϕN
- 243. MFDxrdQϕN
- 244. MFDOxrdQNϕ
- 245. MFDOxPrdQNϕ
- 246. MFDOxPrdSQNϕ
- 247. MFDOxPrdSQNϕ
- 248. Половина длины фокальной хорды (т. е. хорды,
- 249. Половина длины фокальной хорды (т. е. хорды,
- 250. Половина длины фокальной хорды (т. е. хорды,
- 251. Половина длины фокальной хорды (т. е. хорды,
- 252. Половина длины фокальной хорды (т. е. хорды,
- 253. Половина длины фокальной хорды (т. е. хорды,
- 254. Половина длины фокальной хорды (т. е. хорды,
- 255. Половина длины фокальной хорды (т. е. хорды,
- 256. Слайд 256
- 257. Полярное уравнение кривой 2-го порядка
- 258. Скачать презентанцию
Слайды и текст этой презентации
Слайд 18Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
Слайд 19Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогдаСлайд 20Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогда
Слайд 25По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 26По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 27По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 40
Докажем обратное: если координаты некоторой точки М(x,y) удовлетворяют уравнению (2),
то для этой точки выполнятся равенство |F1М - F2 М
| = 2a (1)
Слайд 55Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Слайд 56Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Слайд 57Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если
Слайд 58Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если или
Слайд 59Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если или , то
Слайд 66Таким образом, получаем
если
если
Подставим в равенство
(|F1М - F2 М | = 2a)
если выполняется
если , то
Слайд 67Таким образом, получаем
если
если
Подставим в равенство
(|F1М - F2 М | = 2a)
если выполняется
если , то
Слайд 68Таким образом, уравнение (2) есть уравнение гиперболы, т.к. доказано, что
координаты любой точки M (x; y) гиперболы, т.е. любой точки,
для которой выполняется выражение (1) удовлетворяет уравнению (2) и обратно, если два числа x и y удовлетворяет уравнению (2), то точка M (x; y) удовлетворяет соотношению (1), т.е. лежит на гиперболе.Слайд 72 5. Исследование формы гиперболы
Т.к. в каноническое уравнение гиперболы координаты x
и y входят во второй степени
Слайд 73 5. Исследование формы гиперболы
Т.к. в каноническое уравнение гиперболы координаты x
и y входят во второй степени => оси Ox и
Oy являются осями симметрии гиперболы, а начало координат центром симметрии.Слайд 74Из уравнения => что
,т.е. и
Геометрически это означает, что между прямыми x=a и x=-a нет точек гиперболы.
Слайд 75Из уравнения => что
,т.е. и
Геометрически это означает, что между прямыми x=a и x=-a нет точек гиперболы.
Ось симметрии Oy не пересекает гиперболу и называется мнимой осью.
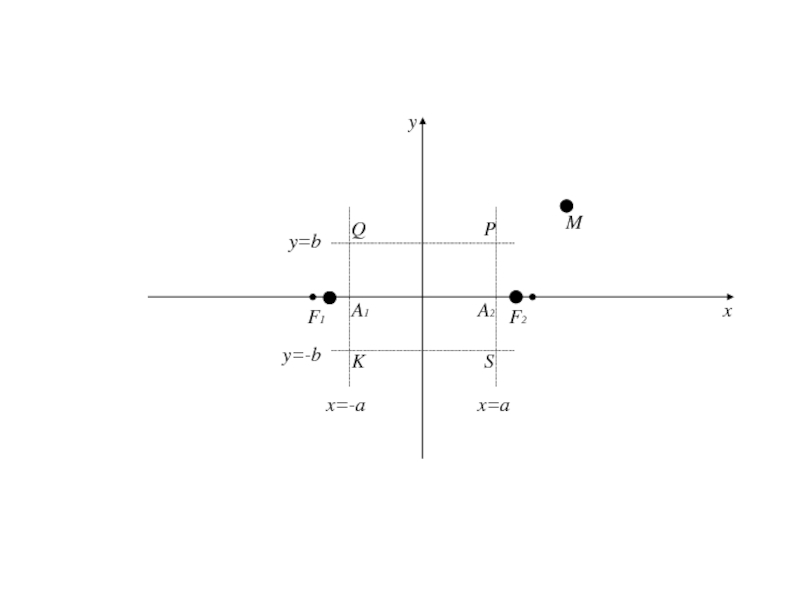
Слайд 76Ось симметрии Ox пересекает гиперболу в двух точках A1(-a;0) A2(a;0)
– вершинах гиперболы и называется действительной осью.
Слайд 77Ось симметрии Ox пересекает гиперболу в двух точках A1(-a;0) A2(a;0)
– вершинах гиперболы и называется действительной осью.
a и b
в уравнении гиперболы называются соответственно действительной и мнимой полуосями гиперболы.Слайд 79Выразим y из уравнения гиперболы и возьмем положительное значение
считая,
что получим точки
гиперболы, лежащие в I четверти.
Слайд 80Выразим y из уравнения гиперболы и возьмем положительное значение
считая,
что получим точки
гиперболы, лежащие в I четверти.Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
Слайд 81Выразим y из уравнения гиперболы и возьмем положительное значение
считая,
что получим точки
гиперболы, лежащие в I четверти.Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
Слайд 82Выразим y из уравнения гиперболы и возьмем положительное значение
считая,
что получим точки
гиперболы, лежащие в I четверти.Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
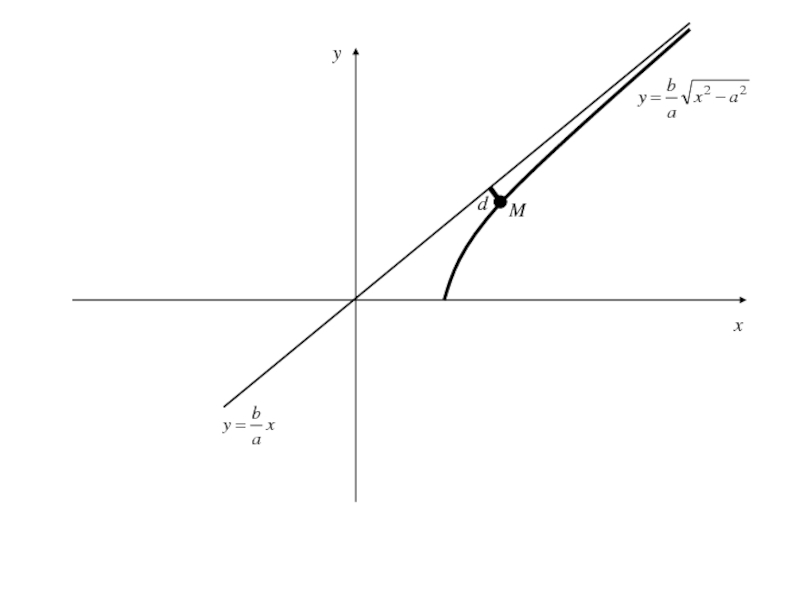
Слайд 83Всякая прямая пересекает гиперболу не более чем в двух точках,
так как прямая определяется уравнением I степени, а гипербола -
II
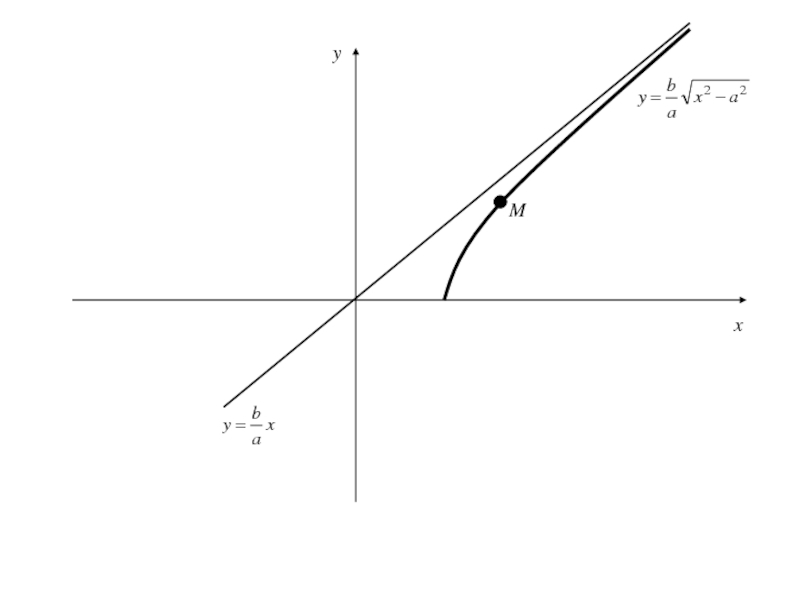
Слайд 84Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 85Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 86Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 87Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 88Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
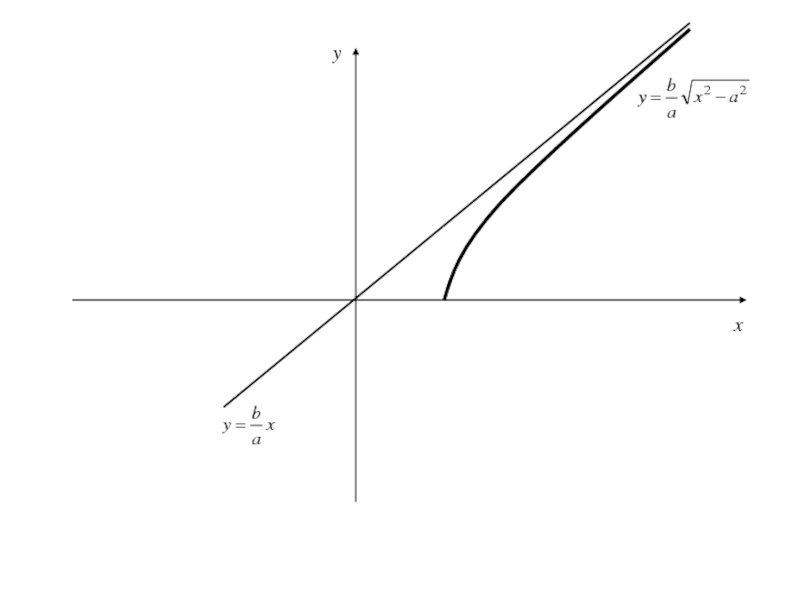
Слайд 89Получили, что на полуинтервале
расстояние d от точки M(x,y) рассматриваемой части гиперболы до
прямой (4) есть убывающая функция и(т.е. расстояние стремиться к 0)
Слайд 90Получили, что на полуинтервале
расстояние d от точки M(x,y) рассматриваемой части гиперболы до
прямой (4) есть убывающая функция и(т.е. расстояние стремиться к 0)
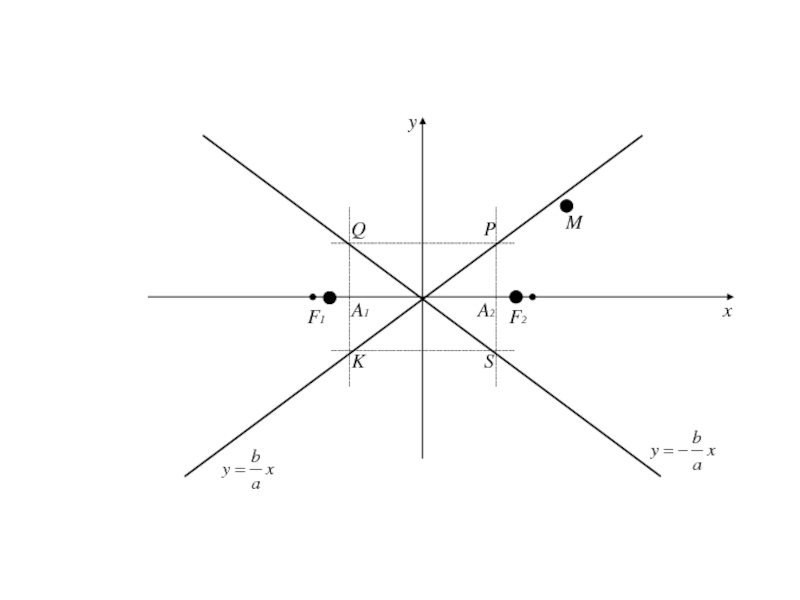
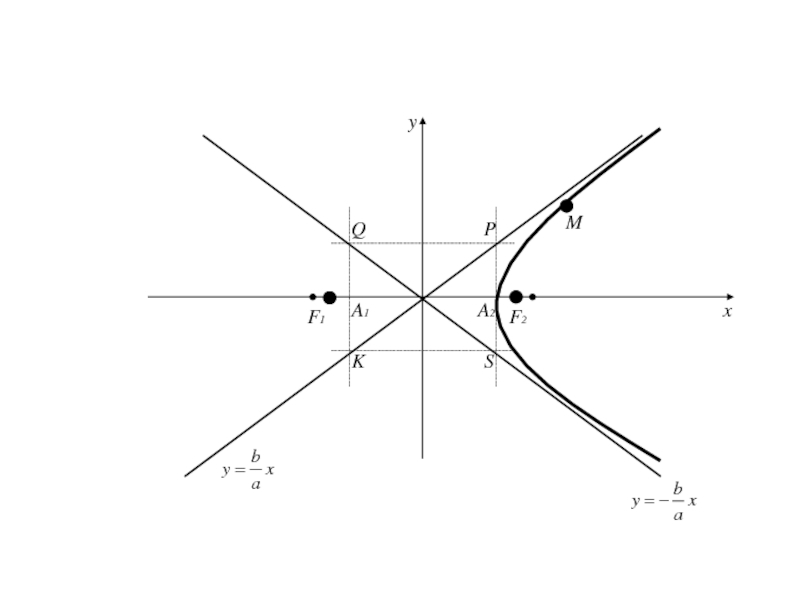
Прямая, определяемая уравнением называется асимптотой гиперболы.
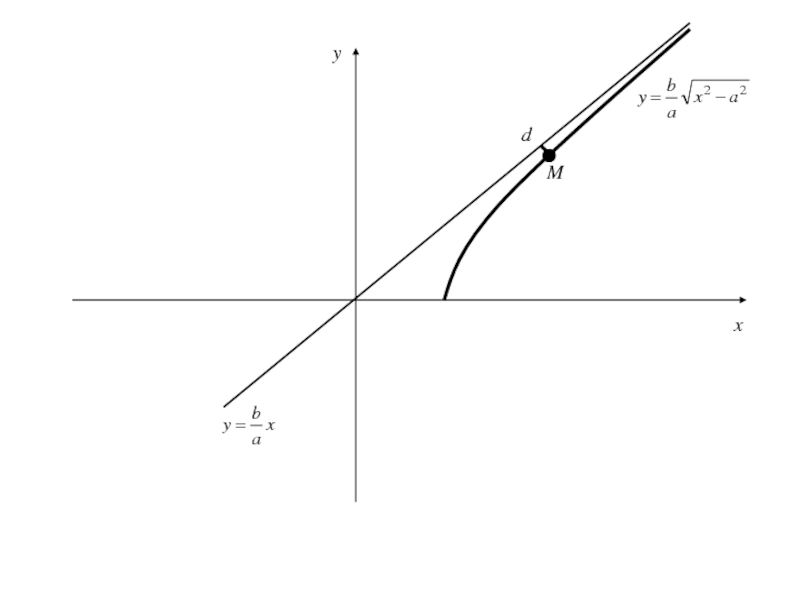
Слайд 96В силу того, что гипербола, заданная каноническим уравнением, симметрична относительно
начала координат, расстояние от точки М(x;y), лежащей на дуге гиперболы,
заданой
уравнением до прямой
стремится к нулю при
Слайд 97Так как гипербола, заданная каноническим уравнением, симметрична относительно оси Оy,
то она имеет вторую асимптоту
которая обладает свойством аналогичным свойству первой
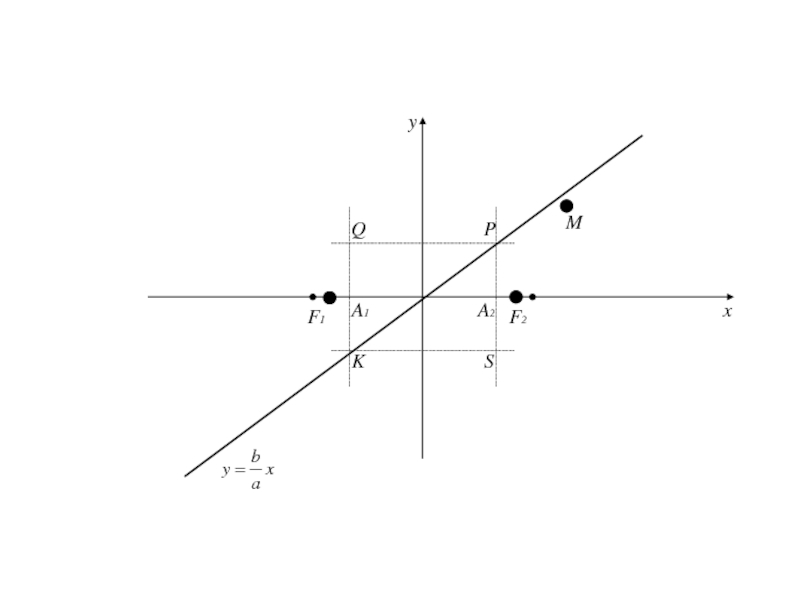
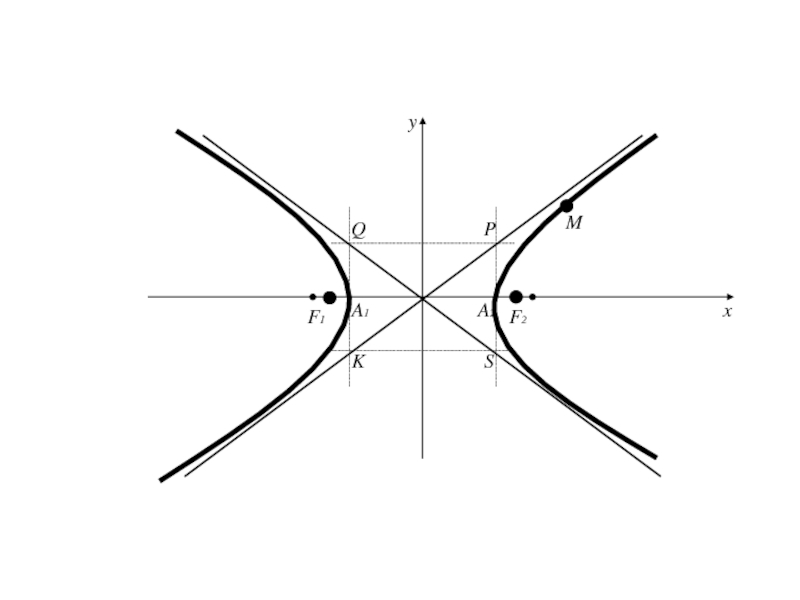
асимптоты по отношению к дугам гиперболы, расположенной в II и IV четвертях .Асимптоты являются диагоналями прямоугольника с вершинами Р(а;b), Q(-a;b), S(a;-b), K(-a;-b).
Слайд 1076. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой еСлайд 1086. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой е
Слайд 1096. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой еТак как для гиперболы 0 < а < с, то е >1
Слайд 112Две прямые, перпендикулярные действительной оси гиперболы и отстоящие от центра
гиперболы на расстояние а/е (где a – действительная полуось, е
– эксцентриситет гиперболы), называются директрисами гиперболыСлайд 114Для гиперболы, заданной каноническим уравнением
уравнения директрис имеют вид
Т.к. e
>1, то директрисы отстоят от центра на расстоянии меньшем действительной
полуоси.
Слайд 117Теорема: Для того чтобы точка лежала на гиперболе, необходимо и
достаточно, чтобы
отношение расстояния от этой точки до фокуса гиперболы
к расстоянию от той же точки до директрисы, соответствующей рассматриваемому фокусу, было равно эксцентриситету гиперболы.Слайд 123 (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой
выполняется
требуется доказать, что
Слайд 124 (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой
выполняется
требуется доказать, что
Найдём
Слайд 125 (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 126 (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 127 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур.(2)(<=)
Слайд 128 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
(<=)
Слайд 129 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
(<=)
Слайд 130 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
(<=)
Слайд 131 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
Возведём в квадрат, упростим, помня, что
(<=)
Слайд 132 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
Возведём в квадрат, упростим, помня, что
получим
(<=)
Слайд 133Самостоятельно изучить вопросы по данной теме:
Понятие сопряженной гиперболы
Уравнение касательной к
гиперболе
Оптическое свойство гиперболы
Слайд 1357. Парабола и её каноническое уравнение
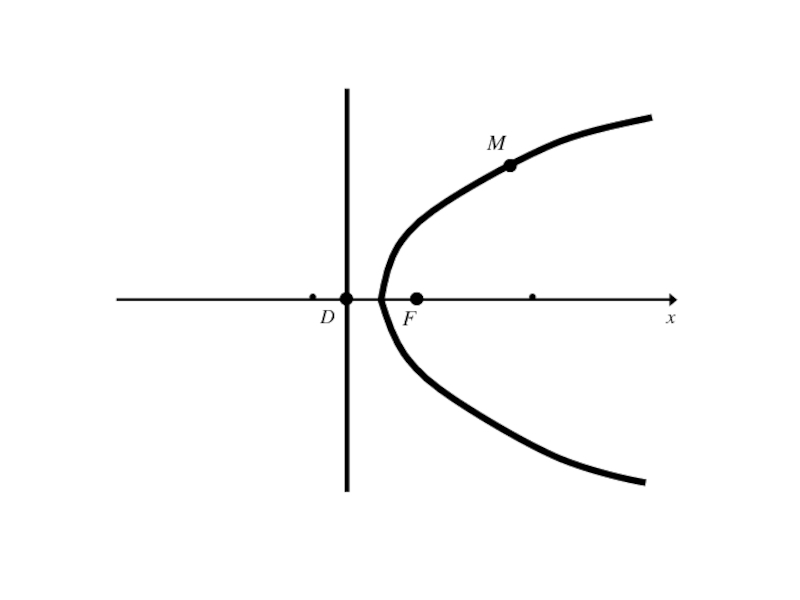
Параболой называется геометрическое место
точек, для каждой из которых расстояние до некоторой фиксированной точки
плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус, и называемой директрисой.Слайд 1367. Парабола и её каноническое уравнение
Расстояние от фокуса параболы
до её директрисы называется параметром параболы.
Слайд 1377. Парабола и её каноническое уравнение
Расстояние от фокуса параболы
до её директрисы называется параметром параболы.
Эксцентриситет параболы принимается равным 1
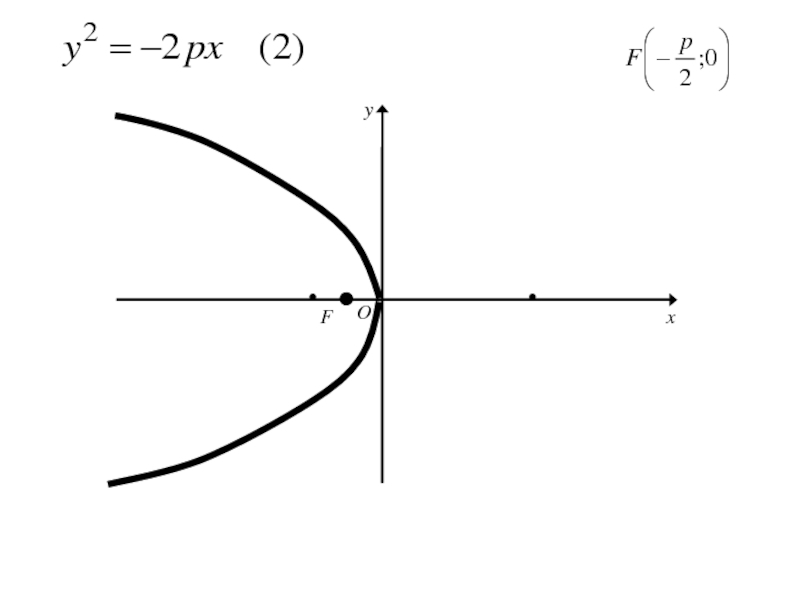
Слайд 146Расстояние FD обозначим р (параметр параболы).
тогда в выбранной системе координат
фокус F будет иметь координаты
Слайд 147Расстояние FD обозначим р (параметр параболы).
тогда в выбранной системе координат
фокус F будет иметь координаты F( ;0)
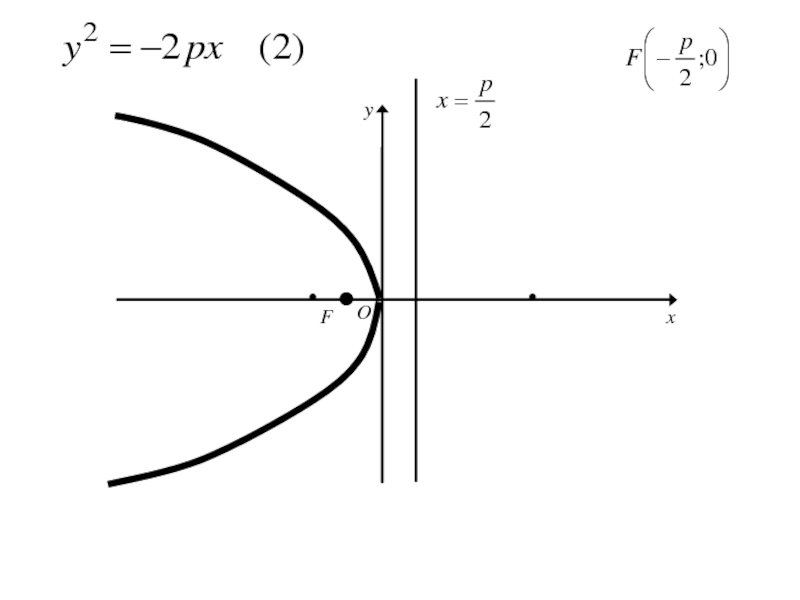
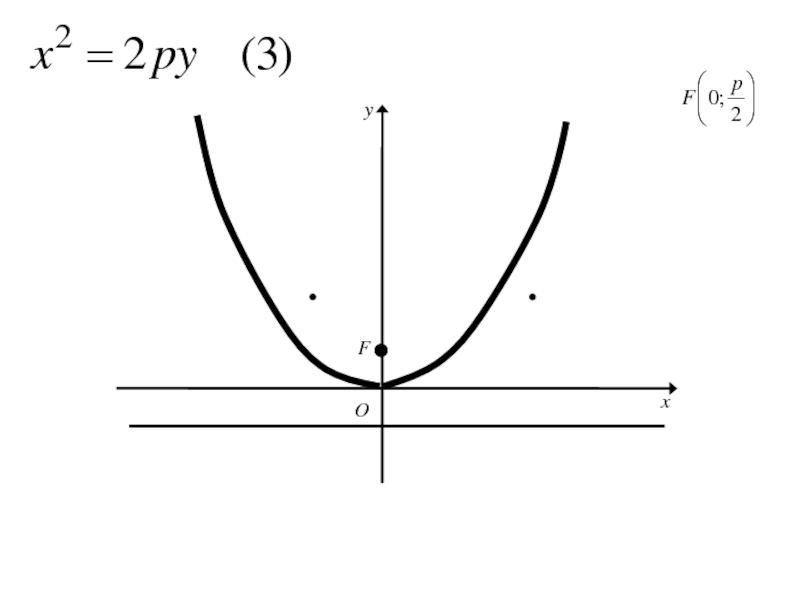
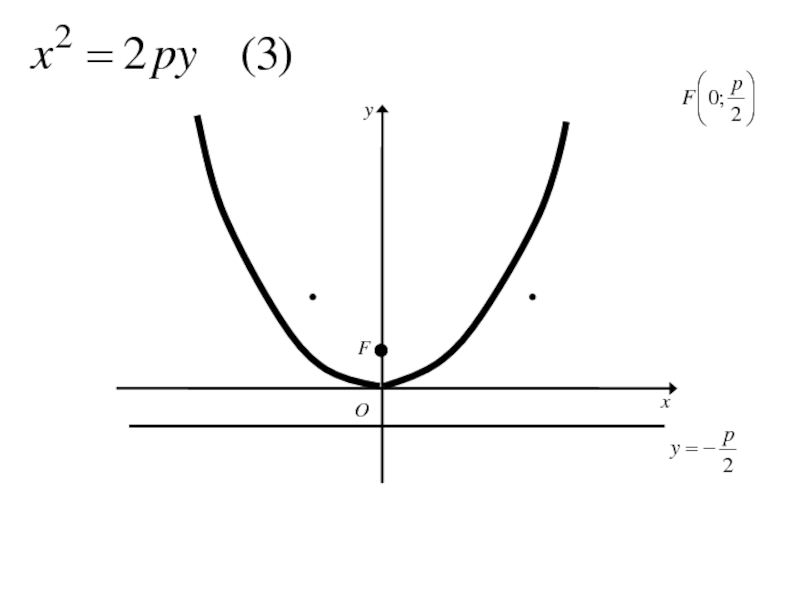
Слайд 148Расстояние FD обозначим р (параметр параболы).
тогда в выбранной системе координат
фокус F будет иметь координаты F( ;0)
а уравнение
директрисы
Слайд 149Расстояние FD обозначим р (параметр параболы).
тогда в выбранной системе координат
фокус F будет иметь координаты F( ;0)
а уравнение
директрисы x=-
Слайд 158Точка M(x;y) лежит на данной параболе тогда и только тогда,
когда r = d
r=|FM|=
d=|PM|=
То уравнение параболы примет вид
Слайд 1658. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то
Слайд 1668. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то ось Ox является осью симметрии
параболы (1).Слайд 1678. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то ось Ox является осью симметрии
параболы (1).Точка пересечения параболы с её осью симметрии называется вершиной параболы.
Слайд 1688. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то ось Ox является осью симметрии
параболы (1).Точка пересечения параболы с её осью симметрии называется вершиной параболы.
Имеет только одну вершину в точке
Слайд 1698. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то ось Ox является осью симметрии
параболы (1).Точка пересечения параболы с её осью симметрии называется вершиной параболы.
Имеет только одну вершину в точке О(0;0).
Слайд 1718. Исследование формы параболы
Всякая прямая пересекает параболу не более чем
в двух точках (т.к. прямая определяется уравнением 1-ой степени, а
парабола - уравнением 2-ой степени)Слайд 175Из (1) ⇒, что x≥0 (т. к. p>0, а
Разрешая уравнение (1) относительно
у и беря лишь неотрицательные значения Слайд 176Из (1) ⇒, что x≥0 (т. к. p>0, а
Разрешая уравнение (1) относительно
у и беря лишь неотрицательные значения видим, что в полуинтервале [0;+∞],
Слайд 177Из (1) ⇒, что x≥0 (т. к. p>0, а
Разрешая уравнение (1) относительно
у и беря лишь неотрицательные значения видим, что в полуинтервале [0;+∞],
y - возрастающая функция, причем
Слайд 178Из (1) ⇒, что x≥0 (т. к. p>0, а
Разрешая уравнение (1) относительно
у и беря лишь неотрицательные значения видим, что в полуинтервале [0;+∞],
y - возрастающая функция, причем
Слайд 184Уравнение
, где р>0,
сводиться к
уравнению (1) заменой x на −x, т. е. путём преобразования системы координат, которая соответствует изменению положительного направления оси Ox на противоположное.
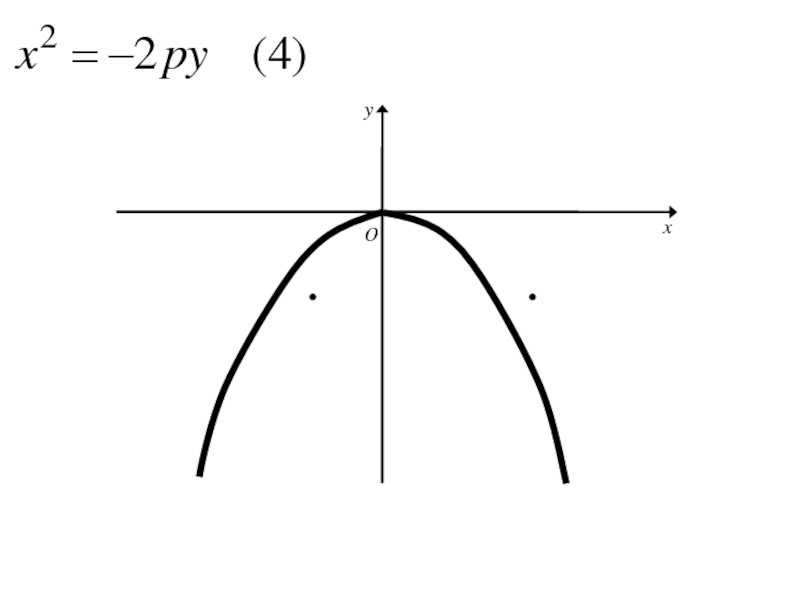
Слайд 185Уравнение
, где р>0,
сводиться к
уравнению (1) заменой x на −x, т. е. путём преобразования системы координат, которая соответствует изменению положительного направления оси Ox на противоположное.
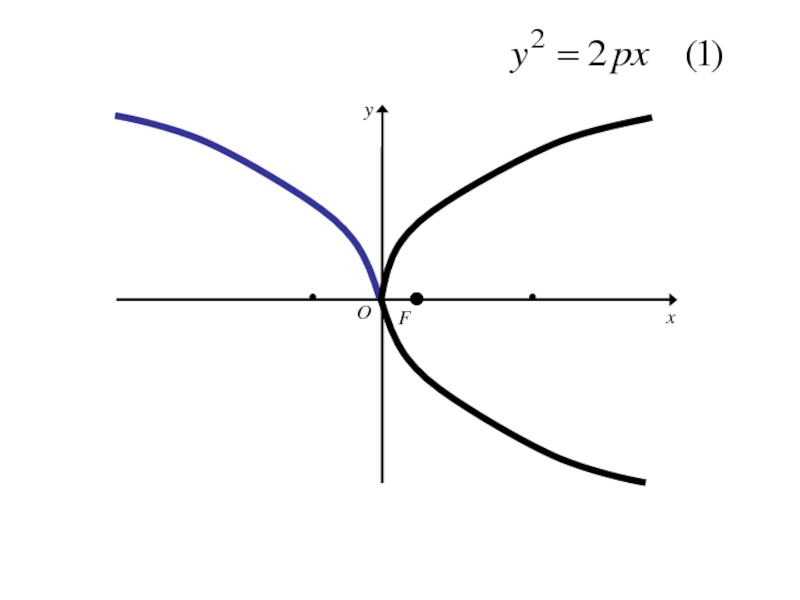
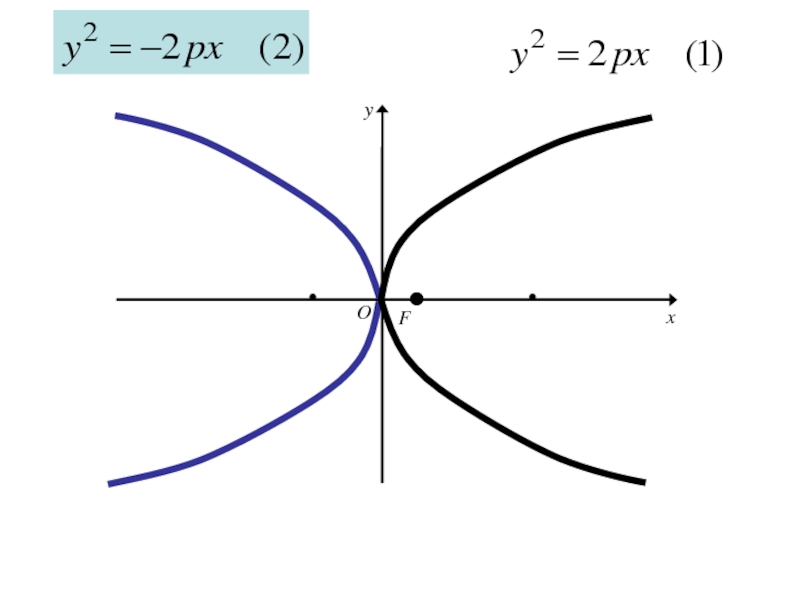
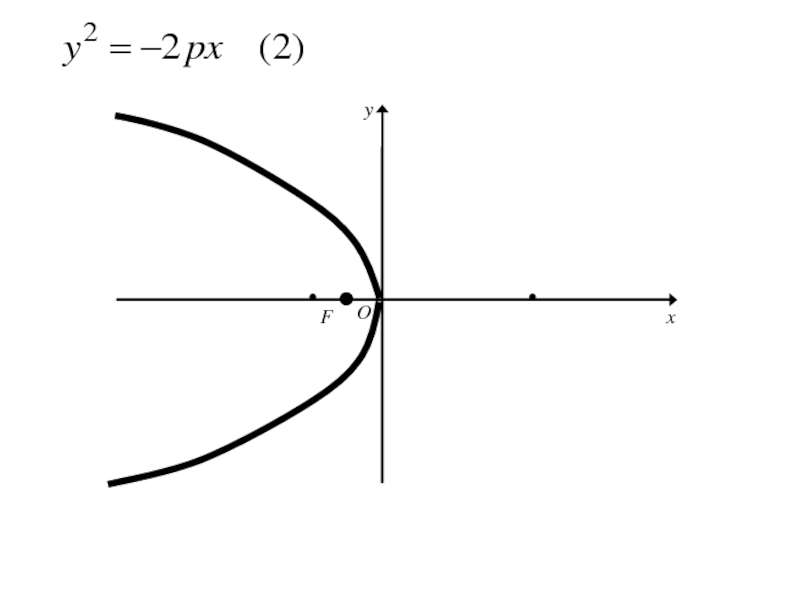
Отсюда следует, что парабола
симметрична с параболой
относительно оси Oy
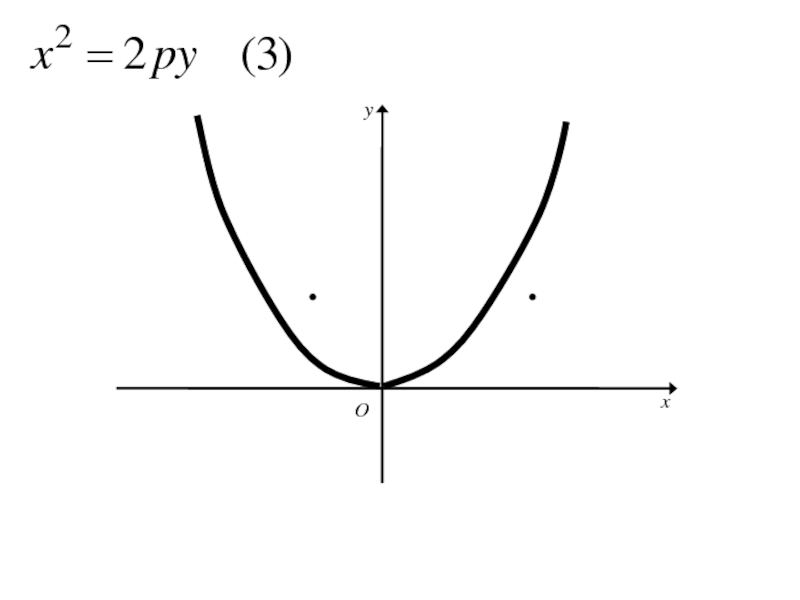
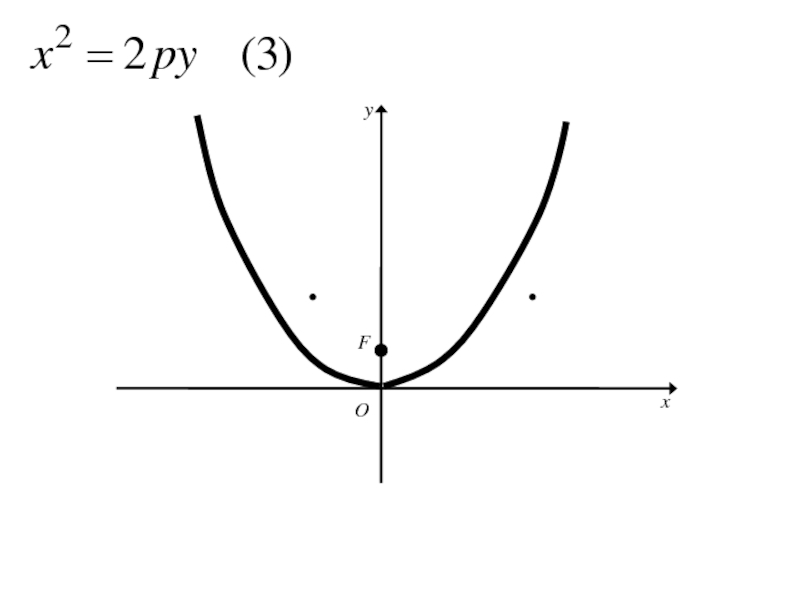
Слайд 194Аналогичными рассуждениями устанавливаем, что каждое из уравнений
где p>0
определяет
параболу с вершиной в начале координат и осью симметрии Oy
Слайд 209Самостоятельно изучить вопросы по данной теме:
Уравнение касательной к параболе
Оптическое свойство
параболы
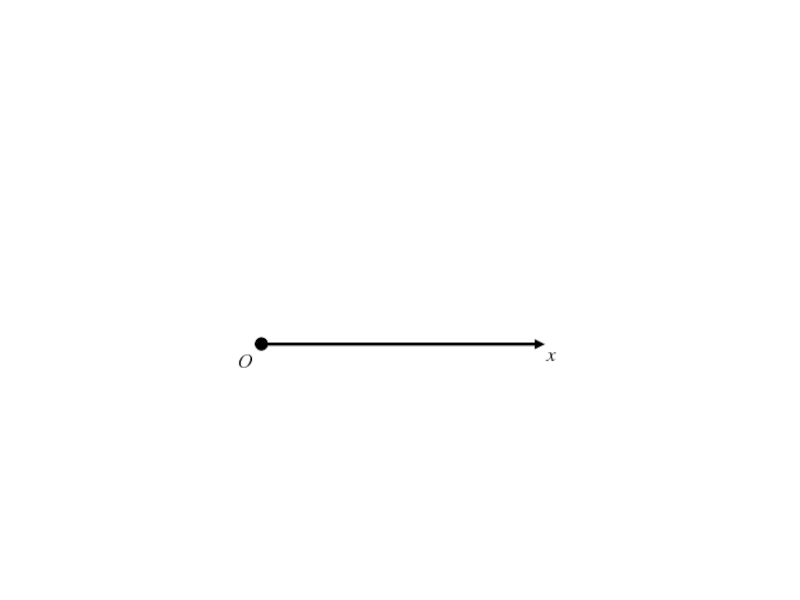
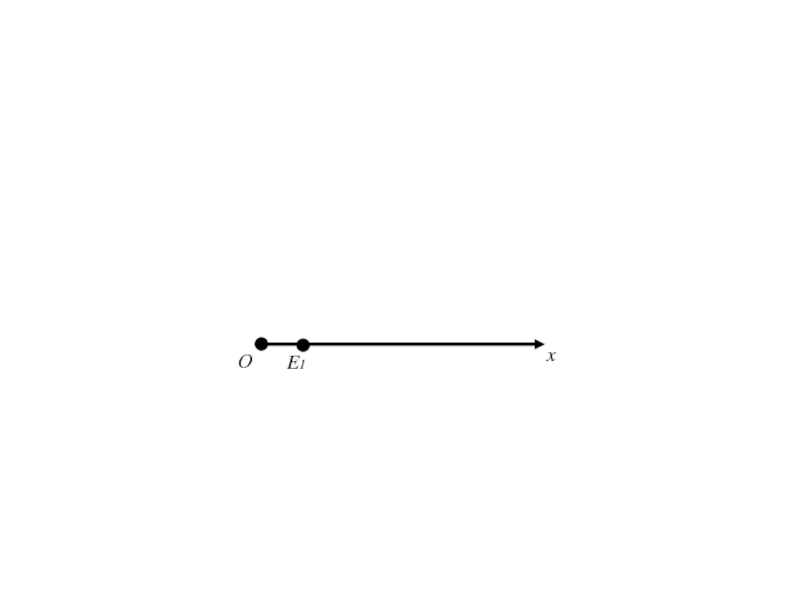
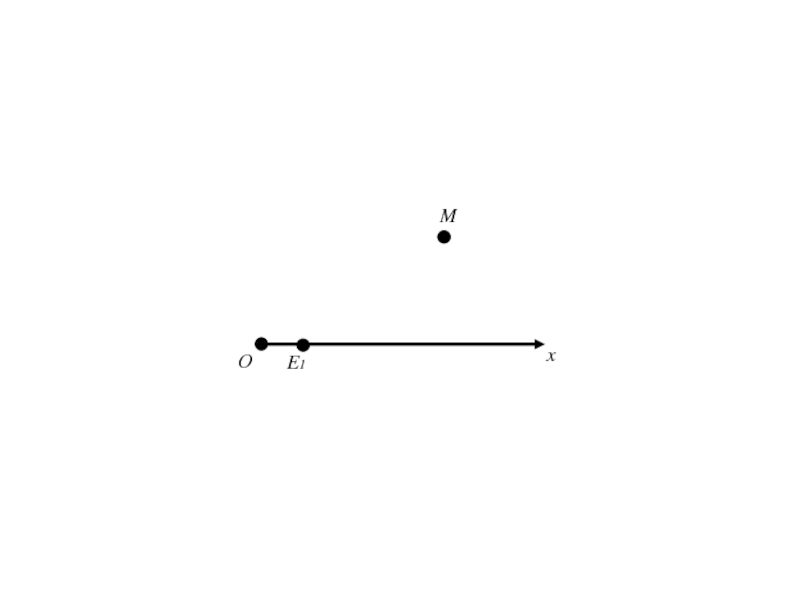
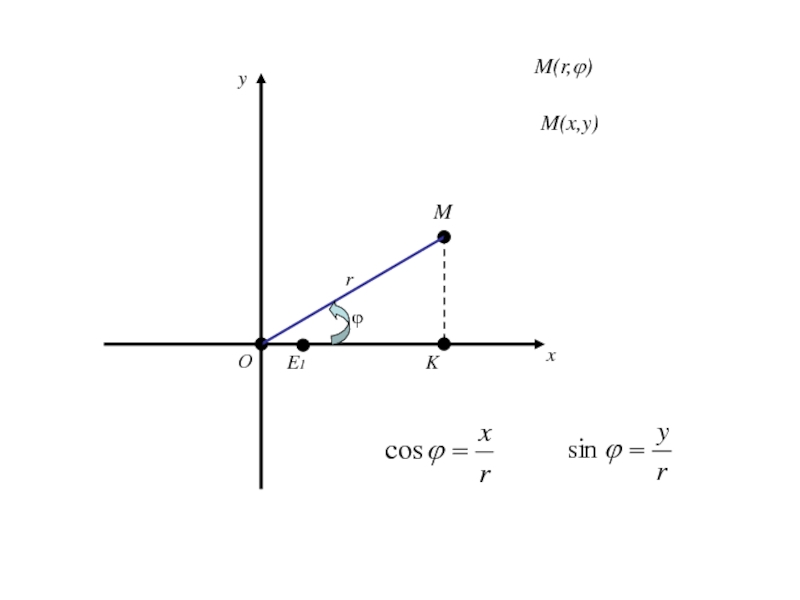
Слайд 211Полярная система координат на плоскости.
Говорят, что на плоскости введена
полярная система координат, если эта плоскость ориентирована, на ней выбраны
точка О – полюс, луч Ох, выходящий из точки О - полярная ось и масштабный отрезок.Слайд 232Формулы (1) позволяют вычислить декартовые прямоугольные координаты х, у точки
М по её полярным координатам ϕ,r.
Слайд 233Формулы (1) позволяют вычислить декартовые прямоугольные координаты х, у точки
М по её полярным координатам ϕ,r.
Формулы (2) и (3) позволяют
вычислить полярные координаты ϕ и r, по её декартовым координатам х, у .Слайд 234Полярное уравнение эллипса, гиперболы и параболы
Пусть L-какая-нибудь из изученных
нами линий второго порядка,
(если L-гипербола, то имеем в виду
одну из её ветвей). Слайд 235Полярное уравнение эллипса, гиперболы и параболы
Пусть L-какая-нибудь из изученных
нами линий второго порядка,
(если L-гипербола, то имеем в виду
одну из её ветвей). Будем называть фокальной осью линии L, ту из её осей симметрии, которая проходит через фокус этой линии.
Слайд 236Введем полярную систему координат, совмещая полюс с фокусом F (в
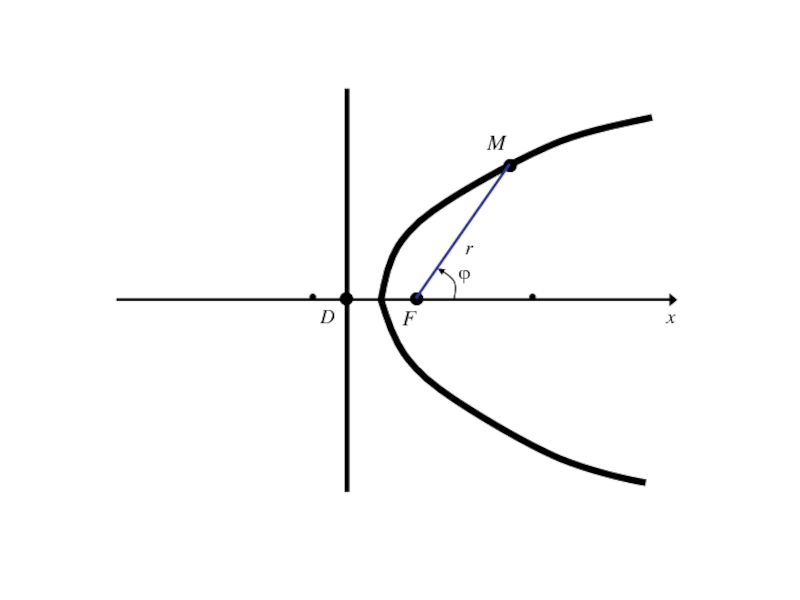
случае гиперболы берем фокус ближайшей к вершине рассматриваемой ветви).
Слайд 237Пусть D-основание перпендикуляра, опущенного из F на директрису, соответствующего этому
фокусу. Полярную ось расположим на прямой DF, причем положительное направление
примем от D к F.Слайд 248Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Слайд 249Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
Слайд 250Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
Слайд 251Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вСлайд 252Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вВыразим r:
Слайд 253Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вВыразим r:
Слайд 254Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вВыразим r:
Слайд 255Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вВыразим r: