Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РАЗДЕЛ НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Содержание
- 1. РАЗДЕЛ НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
- 2. Чертеж – международный язык общения техников. Начертательная
- 3. Базовые геометрические элементы начертательной геометрии
- 4. Точка – абстрактное математическое понятие. Нульмерный объект
- 5. Проективное пространство
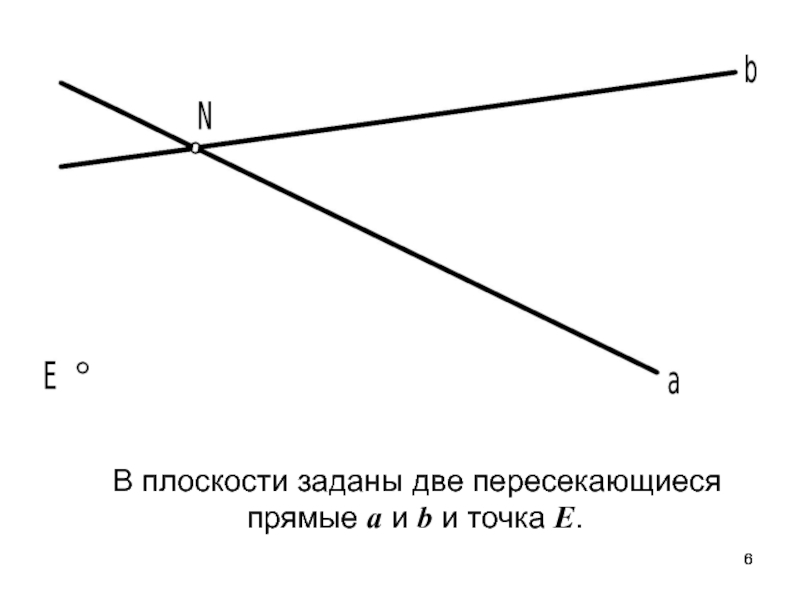
- 6. В плоскости заданы две пересекающиеся прямые a и b и точка E.
- 7. В этой же плоскости через
- 8. Через точку Е проведем прямую l4
- 9. Для устранения неоднородности Евклидова пространства
- 10. Тогда, если l4 b,
- 11. Евклидово пространство, дополненное несобственными элементами, называют проективным.
- 12. Метод проецирования
- 13. Все изображения разные, но их объединяет то,
- 14. Задаем произвольную плоскость Пк
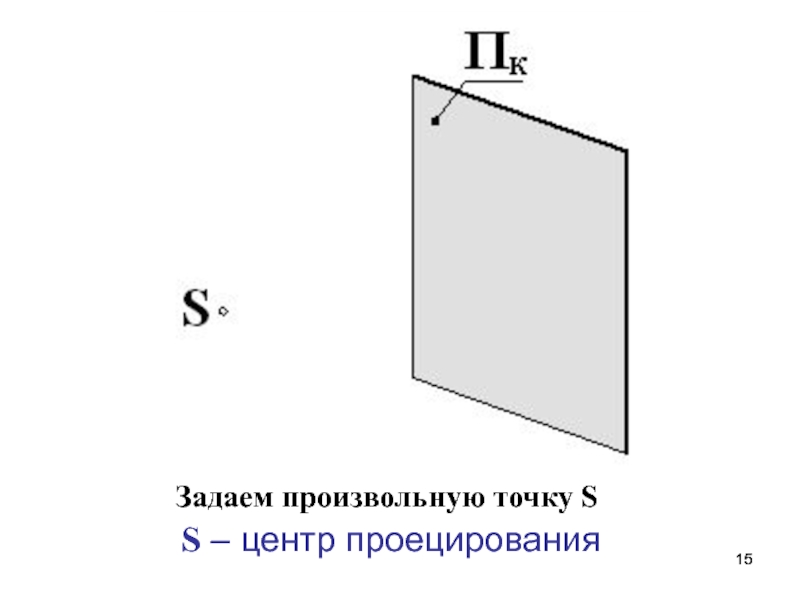
- 15. Задаем произвольную точку S S – центр проецирования
- 16. Аппарат проецированияПк – плоскость проекцийS – центр проецирования
- 17. В качестве объекта взята произвольная точка А
- 18. Для получения изображения точки А на плоскости
- 19. Определим точку пересечения проецирующей прямой SA с
- 20. Для любой точки пространства SA ∩ Пк
- 21. Пк – плоскость проекцийS – центр проецированияSA
- 22. Варианты метода проецирования
- 23. Слайд 23
- 24. Центральное проецирование (коническое) S (центр проецирования)–
- 25. Параллельное проецирование (цилиндрическое)S (центр проецирования) –
- 26. Слайд 26
- 27. Параллельное проецирование
- 28. Слайд 28
- 29. Свойства проецирования
- 30. Общие свойства проецирования
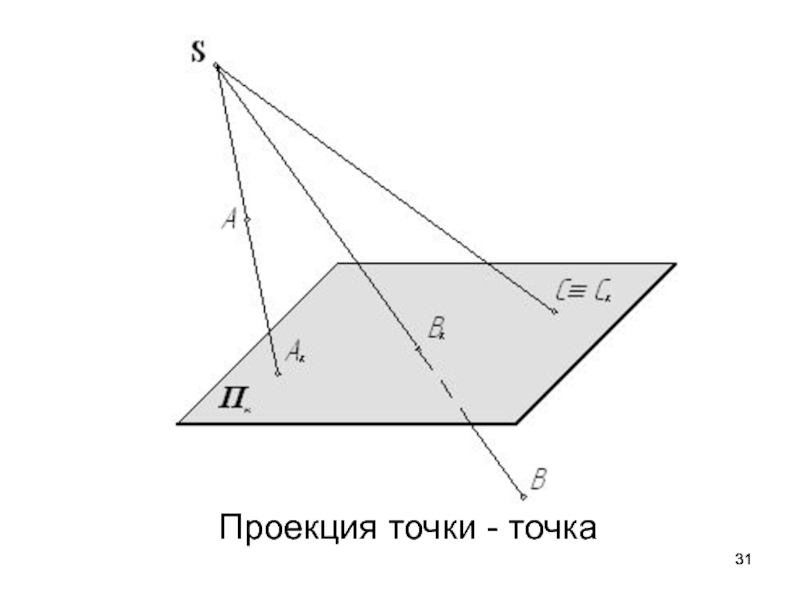
- 31. Проекция точки - точка
- 32. Если точка принадлежит линии, то проекции точки принадлежат одноименным проекциям этой линии.Am Ak mk
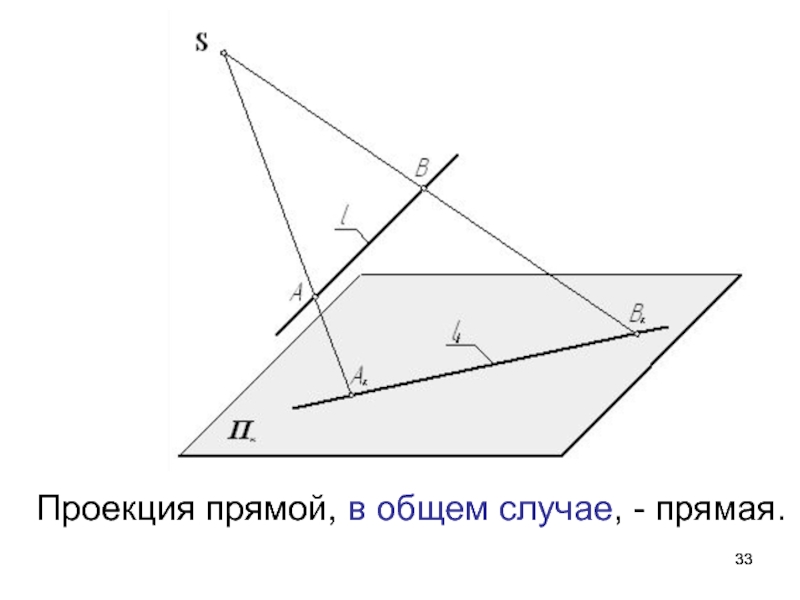
- 33. Проекция прямой, в общем случае, - прямая.
- 34. Если прямая проходит через центр проецирования S
- 35. Если прямые пересекаются, то пересекаются
- 36. Если плоскость проходит через центр
- 37. Если плоская фигура Ф параллельна плоскости проекций
- 38. Инвариантные свойства параллельного проецирования
- 39. Если отрезок прямой разделен в заданном отношении,
- 40. Если прямые параллельны, то их
- 41. Если прямая параллельна плоскости проекций,
- 42. Если плоская фигура параллельна плоскости проекций, то
- 43. Требования, предъявляемые к проекционному изображению
- 44. 1. НаглядностьСвойство, которое дает возможность по изображению представить внешнюю форму заданного объектаmaxmin
- 45. 2. ОбратимостьСвойство, на основе которого по изображению
- 46. 3. Единство правил построения изображения и правил его графического оформления
- 47. Выбор того или иного вида проекции определяется
- 48. Ортогональные проекции
- 49. Возьмем произвольную точку А и плоскость проекций Пк.
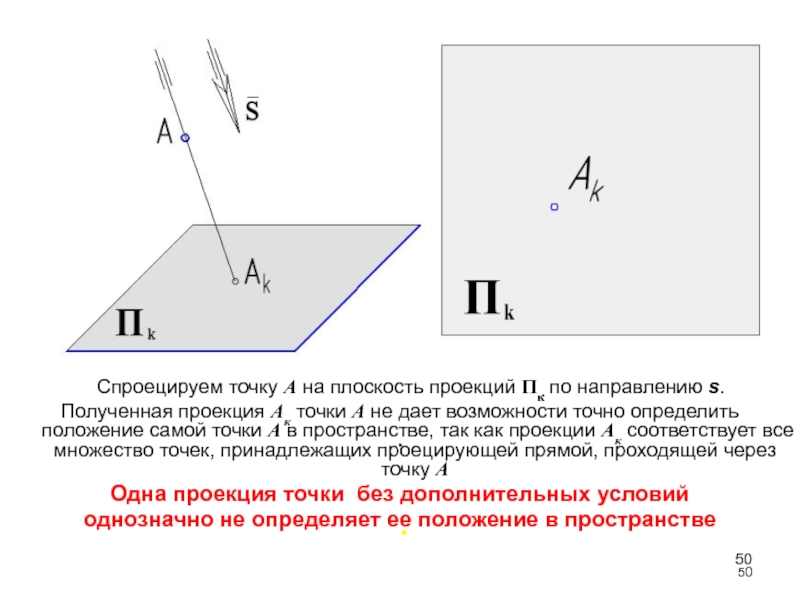
- 50. Спроецируем точку А на плоскость
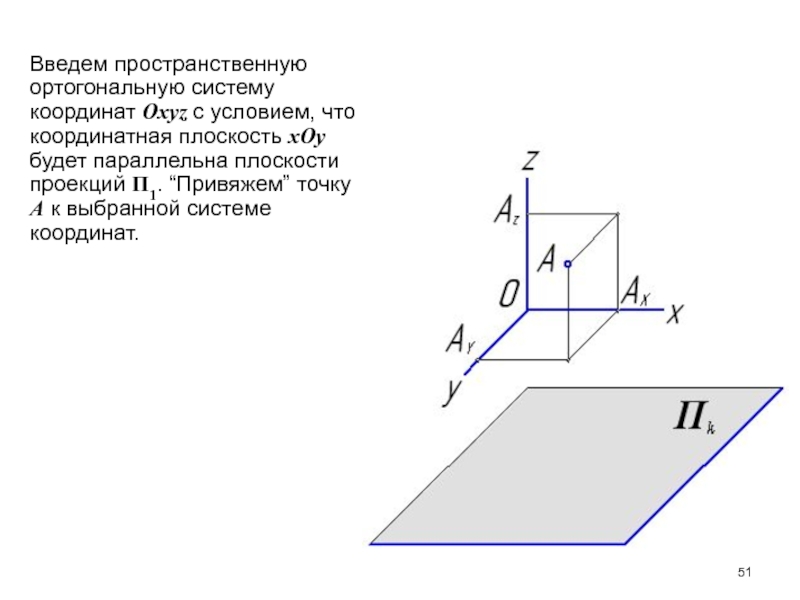
- 51. Введем пространственную ортогональную систему координат Оxyz с
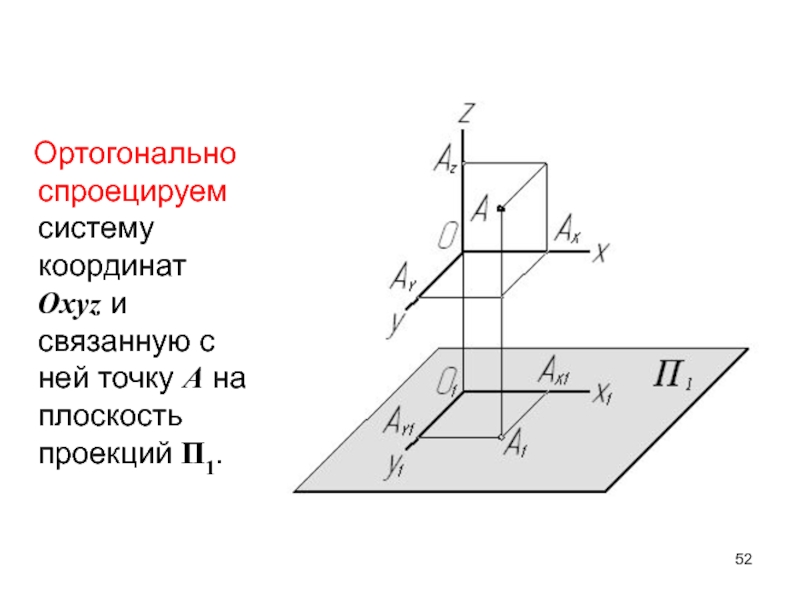
- 52. Ортогонально спроецируем систему координат Oxyz
- 53. В этом случае на проекции
- 54. Введем вторую плоскость проекций П2, параллельную координатной
- 55. Но координатные плоскости xOz и xOy взаимно
- 56. Ортогональные проекции точки на две
- 57. Метод Монжа
- 58. Ортогональная система двух плоскостей проекций
- 59. П1 П2П1
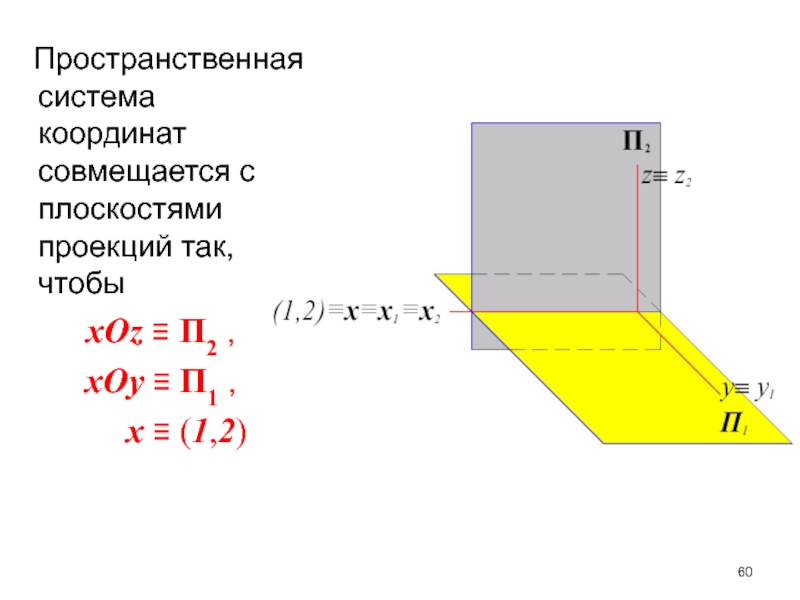
- 60. Пространственная система координат совмещается с
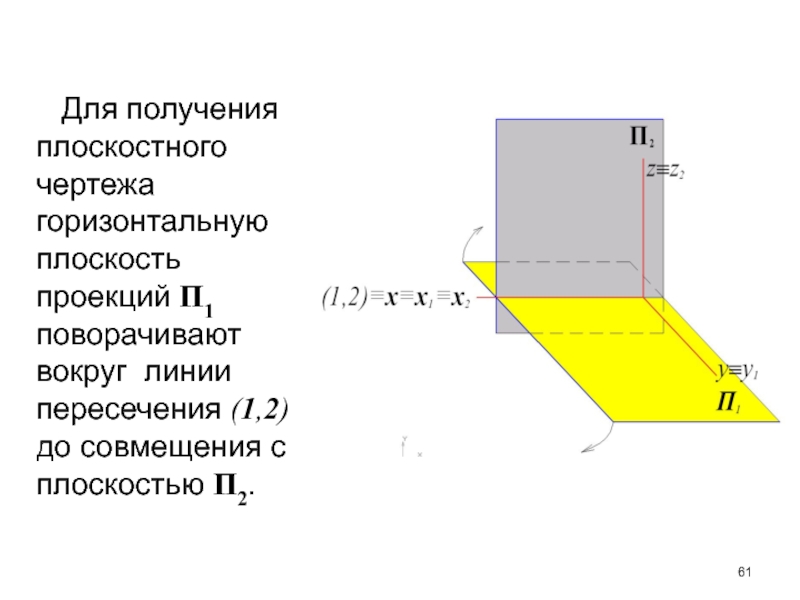
- 61. Для получения плоскостного чертежа горизонтальную
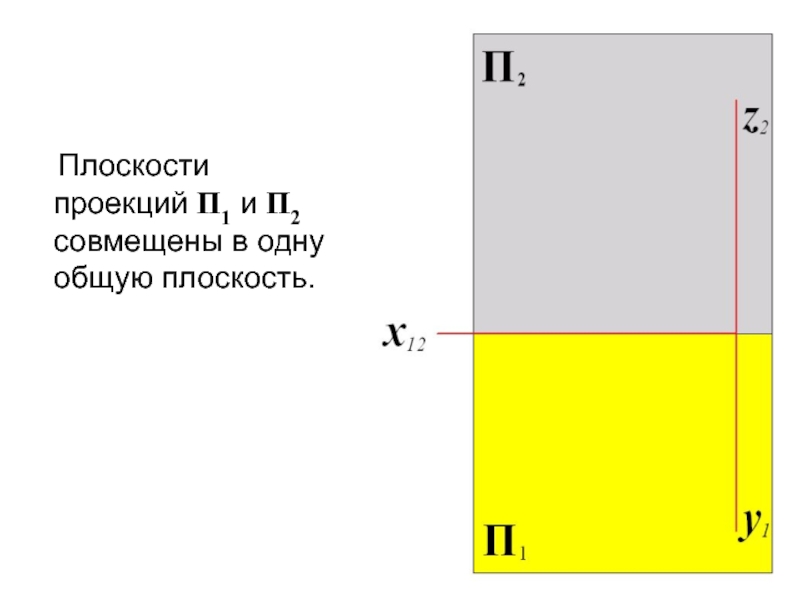
- 62. Плоскости проекций П1 и П2 совмещены в одну общую плоскость.
- 63. Так как плоскости проекций бесконечны, то
- 64. Ортогональная система трех плоскостей проекций
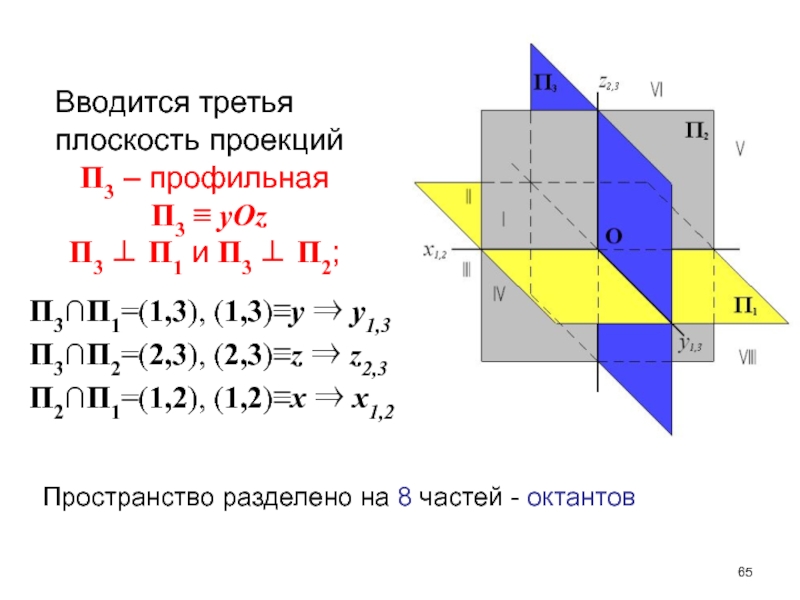
- 65. П3∩П1=(1,3), (1,3)y y1,3П3∩П2=(2,3), (2,3)z z2,3П2∩П1=(1,2),
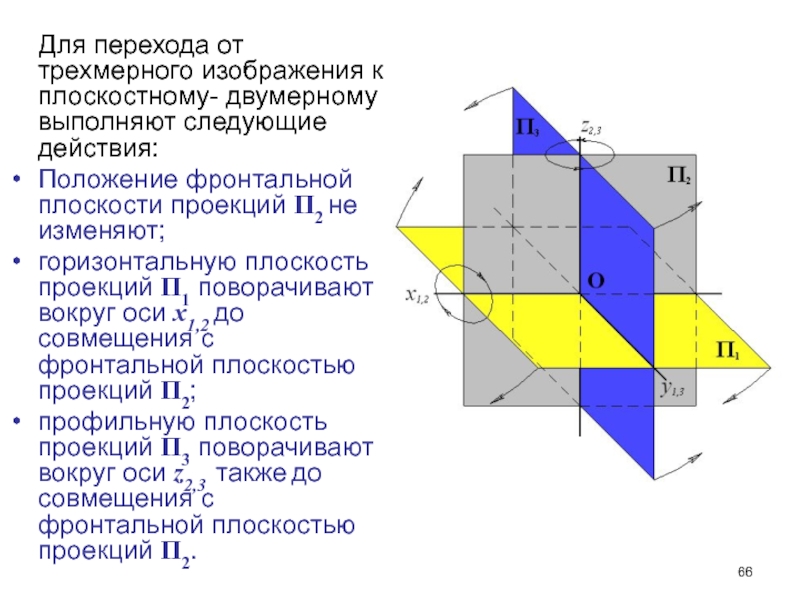
- 66. Для перехода от трехмерного
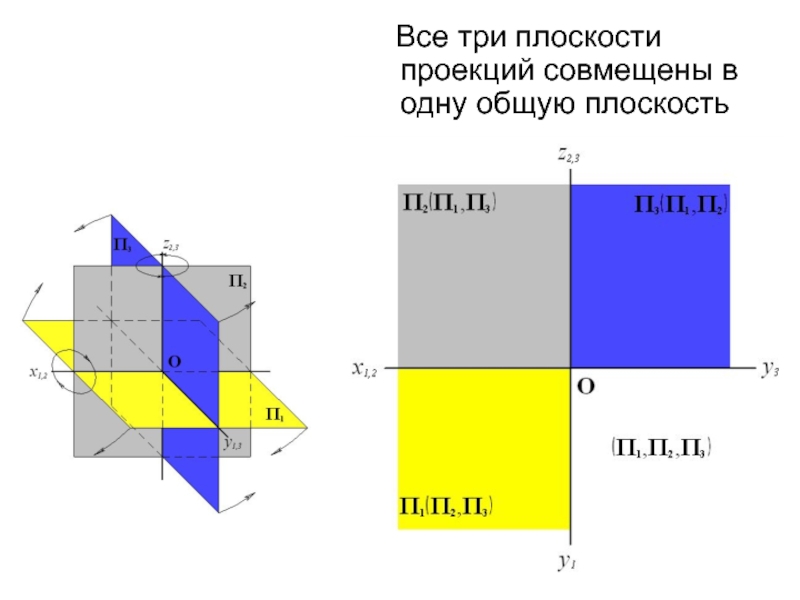
- 67. Все три плоскости проекций совмещены в одну общую плоскость
- 68. Проецирование точки
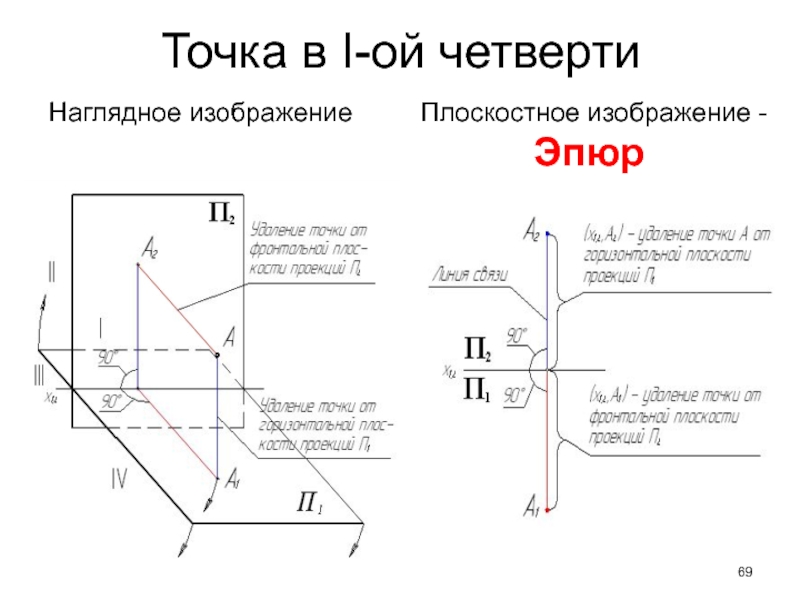
- 69. Точка в I-ой четвертиНаглядное изображениеПлоскостное изображение - Эпюр
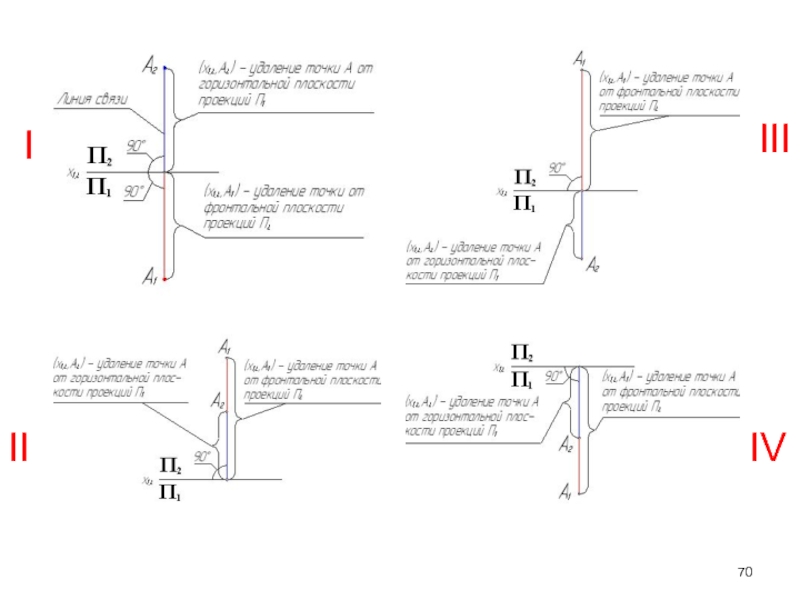
- 70. IIIIIIIV
- 71. Горизонтальная и фронтальная проекции точки
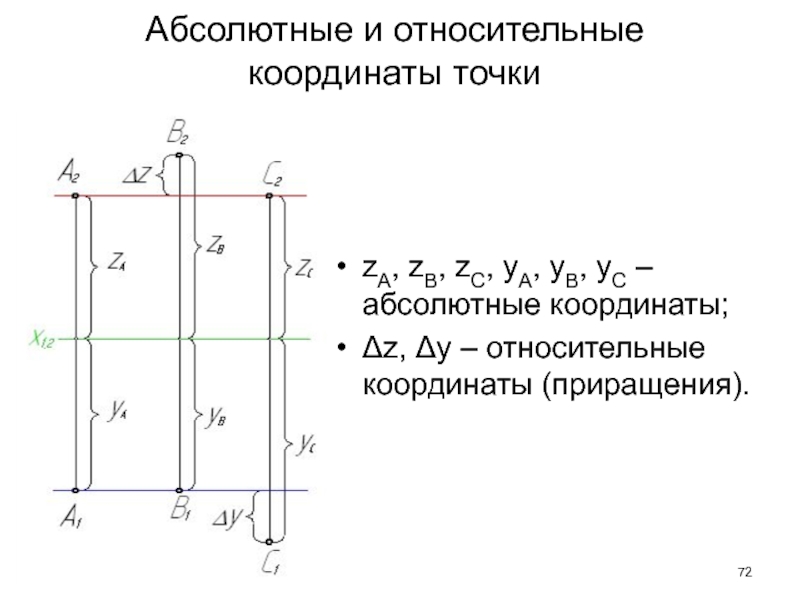
- 72. Абсолютные и относительные координаты точкиzA, zB, zC,
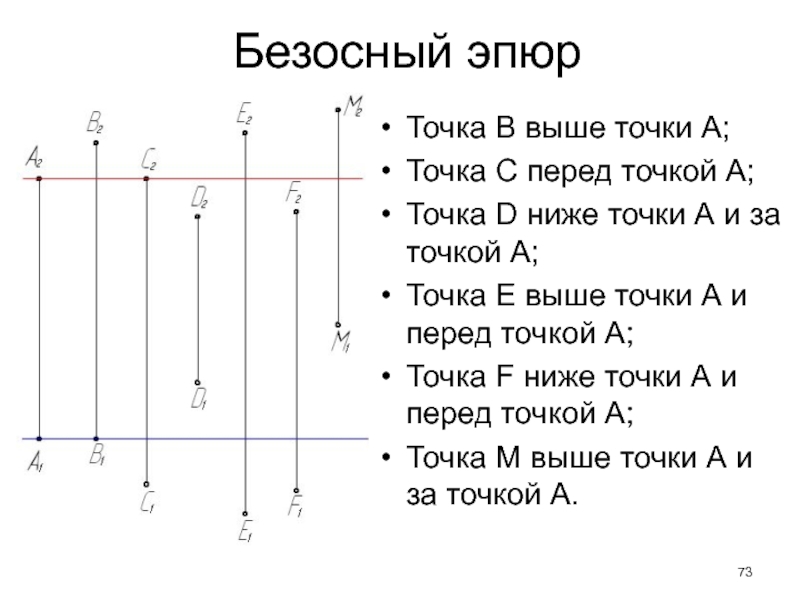
- 73. Безосный эпюрТочка В выше точки А;Точка С
- 74. Проецирование точки в системе трех ортогональных плоскостей проекций
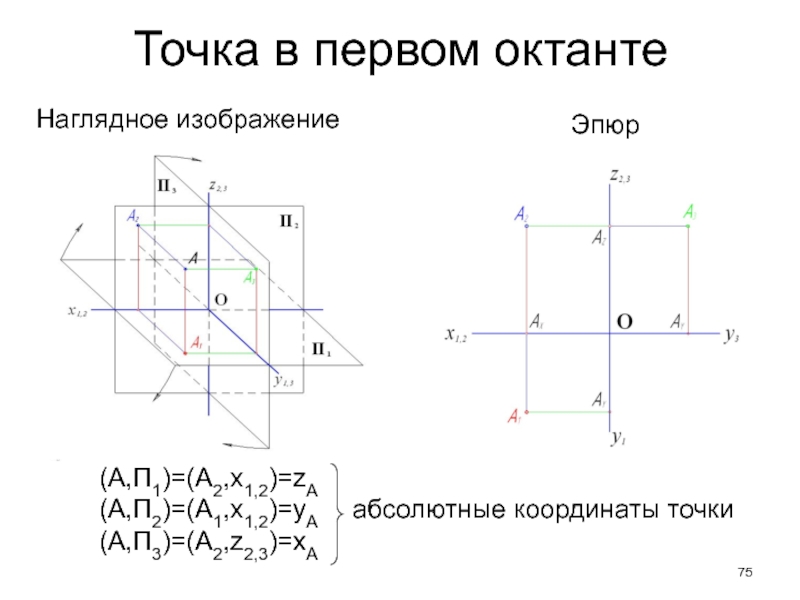
- 75. Точка в первом октантеНаглядное изображениеЭпюр(A,П1)=(А2,х1,2)=zА(A,П2)=(А1,х1,2)=yА абсолютные координаты точки(A,П3)=(А2,z2,3)=хА
- 76. Условия, которым должен удовлетворять эпюр точки, расположенной
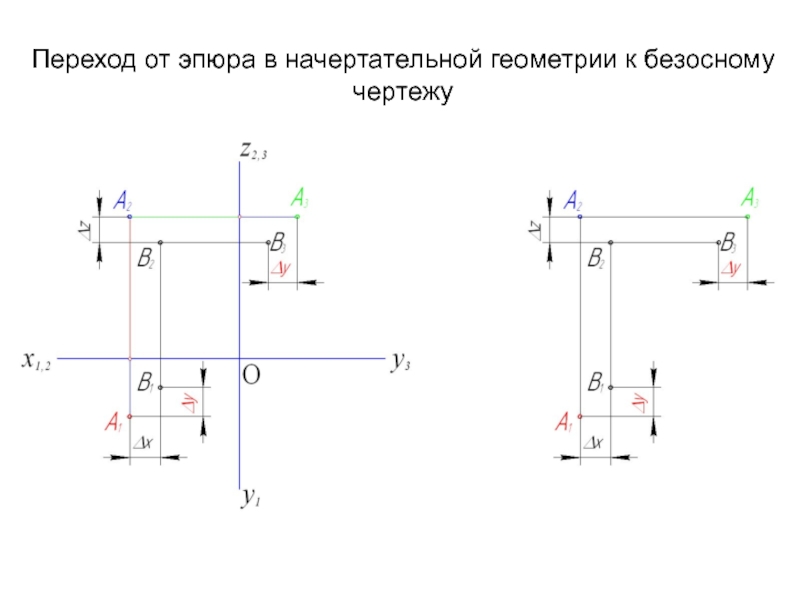
- 77. Переход от эпюра в начертательной геометрии к безосному чертежу
- 78. Скачать презентанцию
Чертеж – международный язык общения техников. Начертательная геометрия – грамматика этого языка (чертежа).Начертательная геометрия изучает методы построения изображений пространственных объектов на плоскости, а также способы преобразования полученных изображений для упрощения решения
Слайды и текст этой презентации
Слайд 2Чертеж – международный язык общения техников.
Начертательная геометрия – грамматика
этого языка (чертежа).
на плоскости, а также способы преобразования полученных изображений для упрощения решения различных инженерных задач.
Слайд 4Точка – абстрактное математическое понятие. Нульмерный объект (не имеет измерений).
Линия
– непрерывное одномерное множество точек ( цепочка точек). Измерение :
только длина. Толщины нет.Поверхность – непрерывное двумерное множество точек. Измерения : длина, ширина, площадь. Толщины и объема нет.
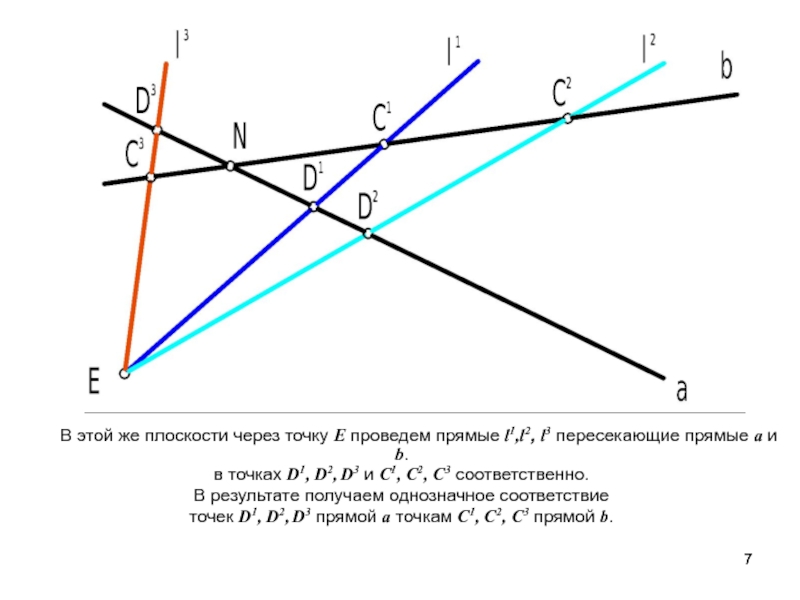
Слайд 7 В этой же плоскости через точку Е проведем
прямые l1,l2, l3 пересекающие прямые a и b.
в точках D1,
D2, D3 и C1, C2, C3 соответственно. В результате получаем однозначное соответствие
точек D1, D2, D3 прямой a точкам C1, C2, C3 прямой b.
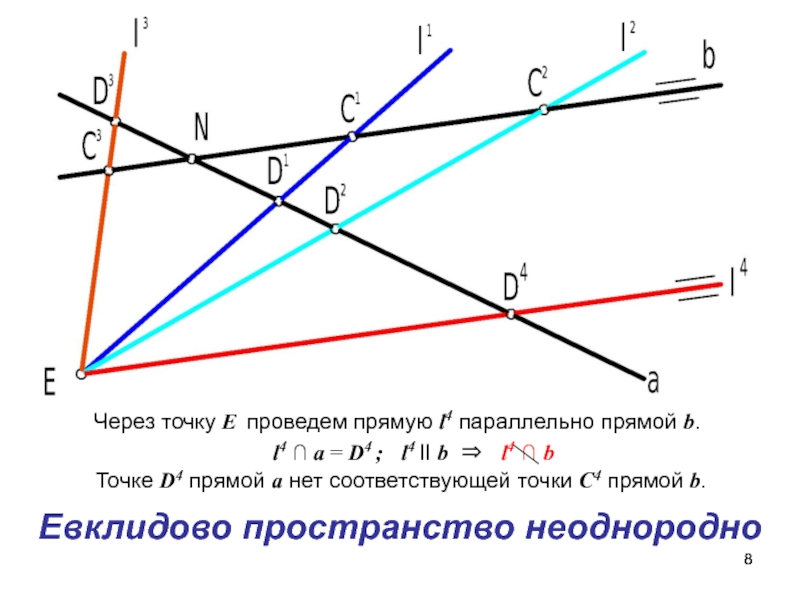
Слайд 8 Через точку Е проведем прямую l4 параллельно прямой b.
l4 ∩ a = D4 ;
l4 II b l4 ∩ bТочке D4 прямой a нет соответствующей точки C4 прямой b.
Евклидово пространство неоднородно
Слайд 9 Для устранения неоднородности Евклидова пространства
(m
n) (m ∩ n = F )
условно принято,
что параллельные
между собой прямые пересекаются
в бесконечно удаленной точке F -
несобственной точке пространства.
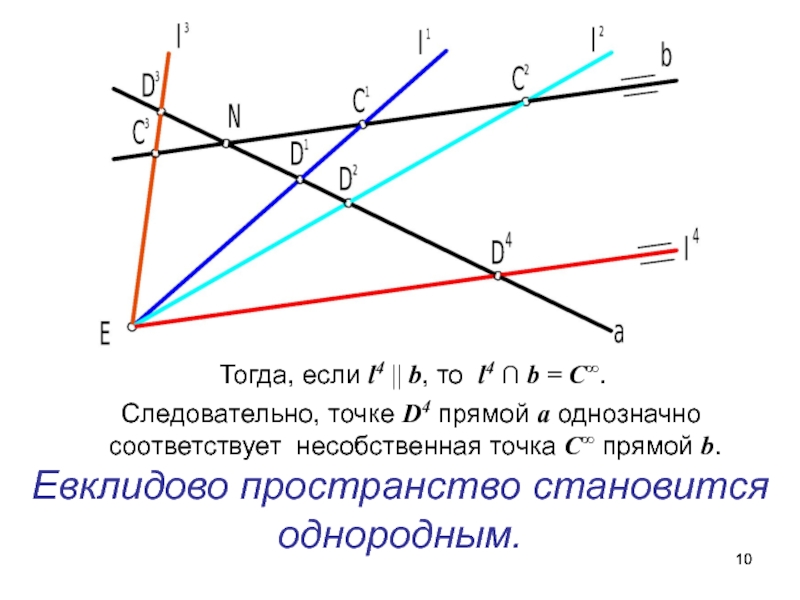
Слайд 10 Тогда, если l4 b, то l4 ∩
b = С.
Следовательно, точке D4 прямой a однозначно
соответствует несобственная точка С прямой b.Евклидово пространство становится однородным.
Слайд 13Все изображения разные, но их объединяет то, что в основе
их построения лежит один и тот же метод – метод
проецирования.Все изображения, построенные на основе метода проецирования, называются проекционными
Перспективная проекция
Аксонометрическая проекция
Ортогональные проекции
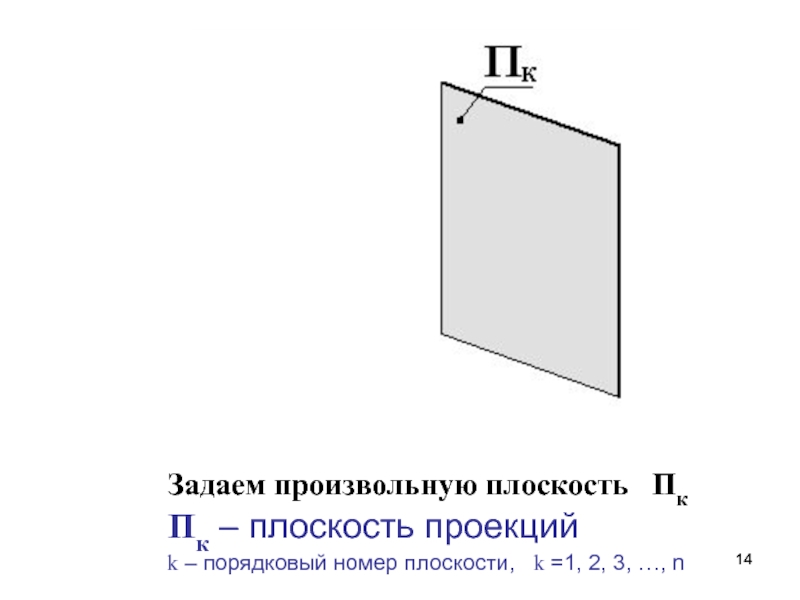
Слайд 14 Задаем произвольную плоскость Пк
Пк –
плоскость проекций
k – порядковый номер плоскости,
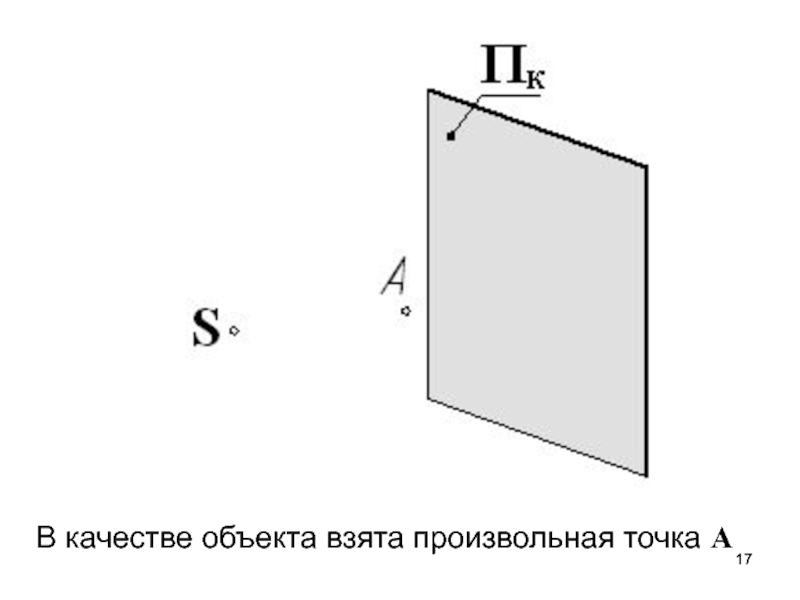
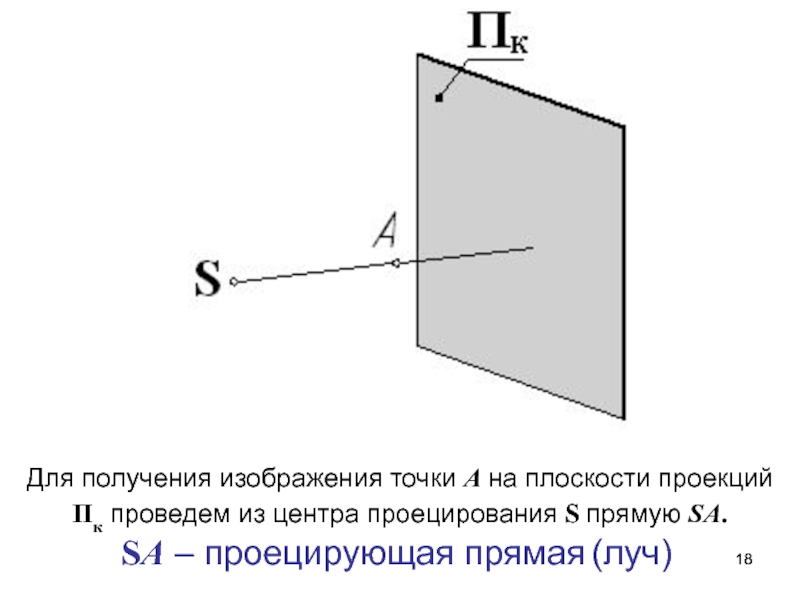
k =1, 2, 3, …, n
Слайд 18Для получения изображения точки А на плоскости проекций Пк проведем
из центра проецирования S прямую SA.
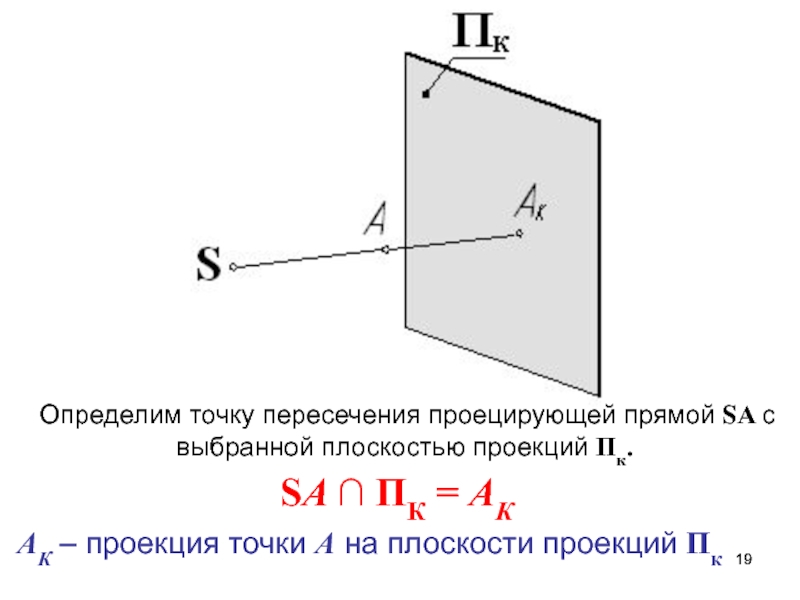
SA – проецирующая прямая (луч)
Слайд 19Определим точку пересечения проецирующей прямой SA с выбранной плоскостью проекций
Пк.
SA ∩ ПК = АК
АК – проекция точки А на
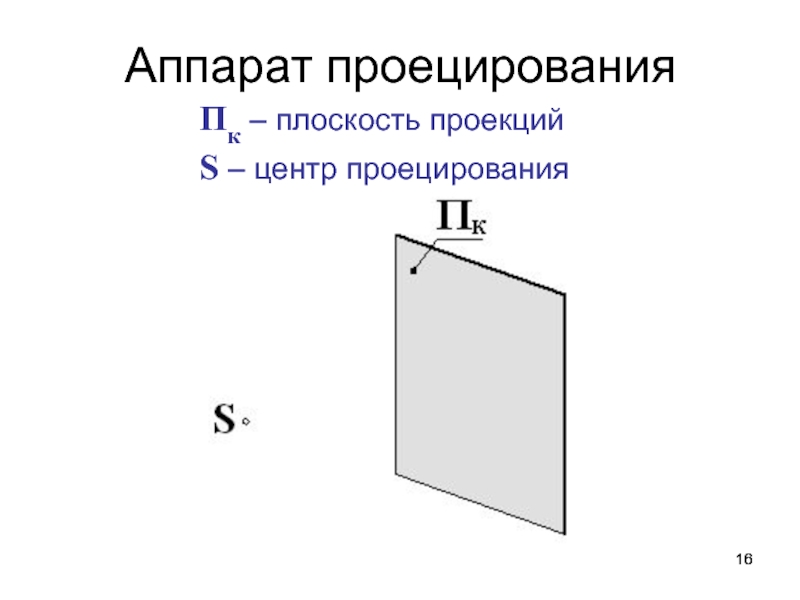
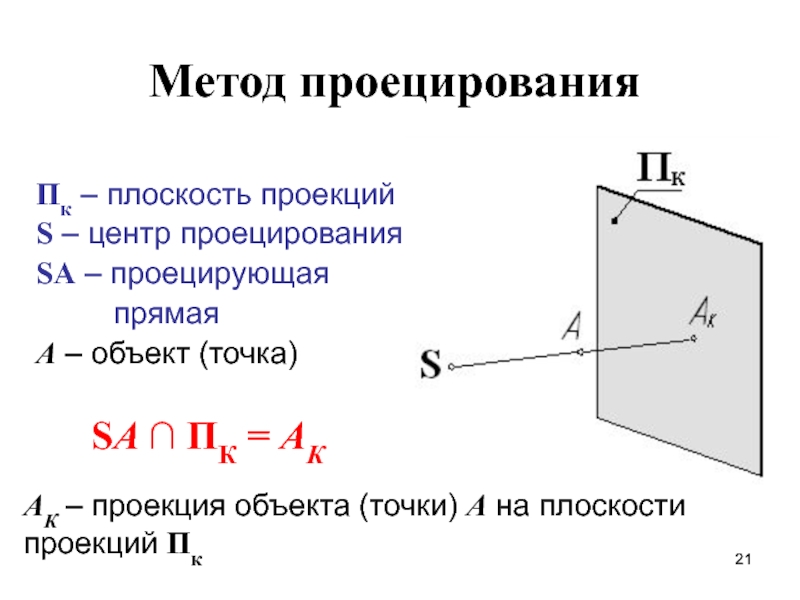
плоскости проекций Пк
Слайд 21Пк – плоскость проекций
S – центр проецирования
SA – проецирующая
прямая
А – объект (точка)
Метод проецирования
SA ∩
ПК = АКАК – проекция объекта (точки) А на плоскости проекций Пк
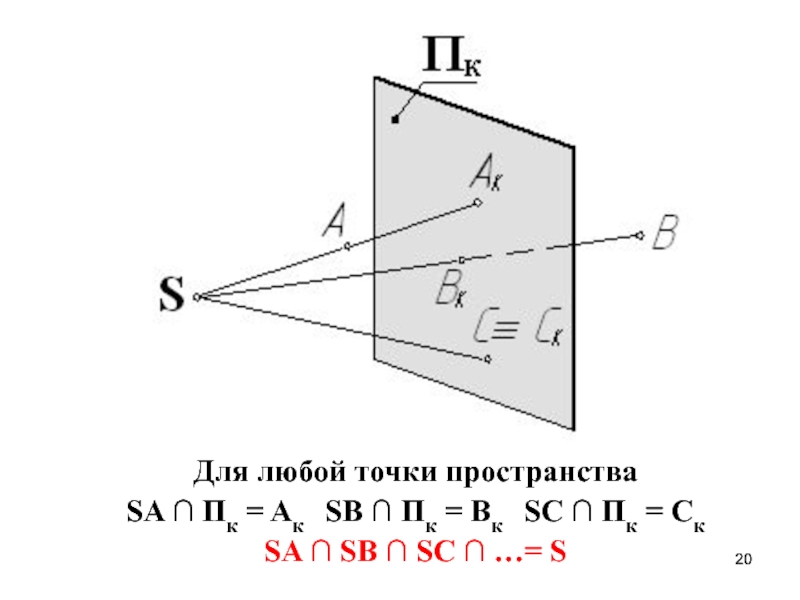
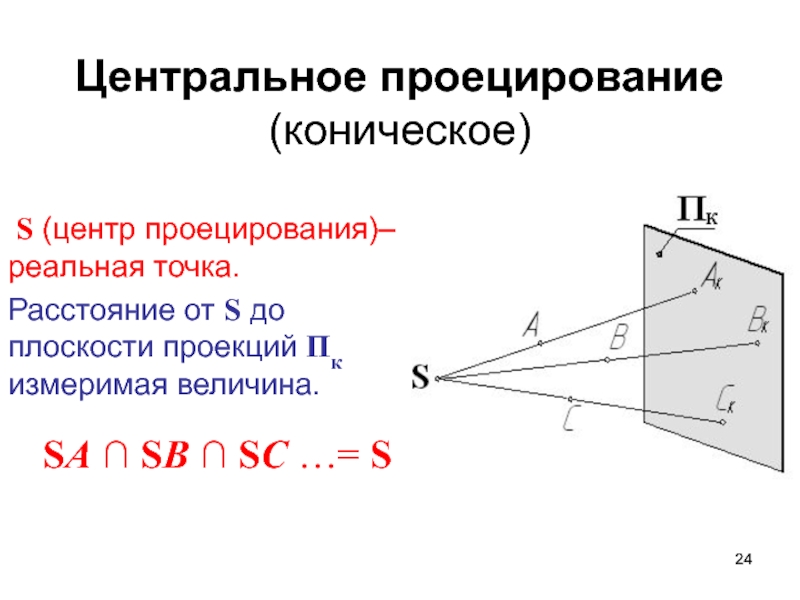
Слайд 24Центральное проецирование
(коническое)
S (центр проецирования)– реальная точка.
Расстояние
от S до плоскости проекций Пк измеримая величина.
SA ∩ SB
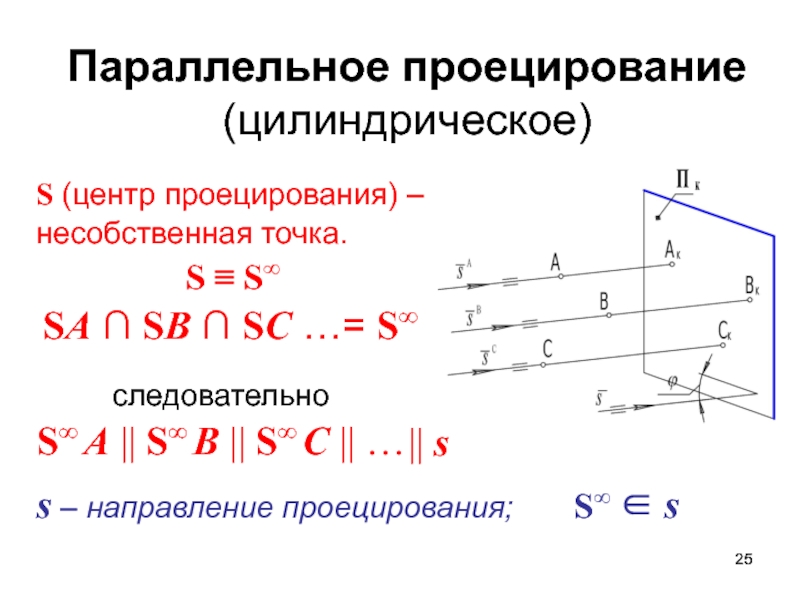
∩ SC …= S
Слайд 25Параллельное проецирование
(цилиндрическое)
S (центр проецирования) –
несобственная точка.
S S
SA ∩ SB ∩ SC …= S
следовательно
S A S B S C …
s – направление проецирования; S s
s
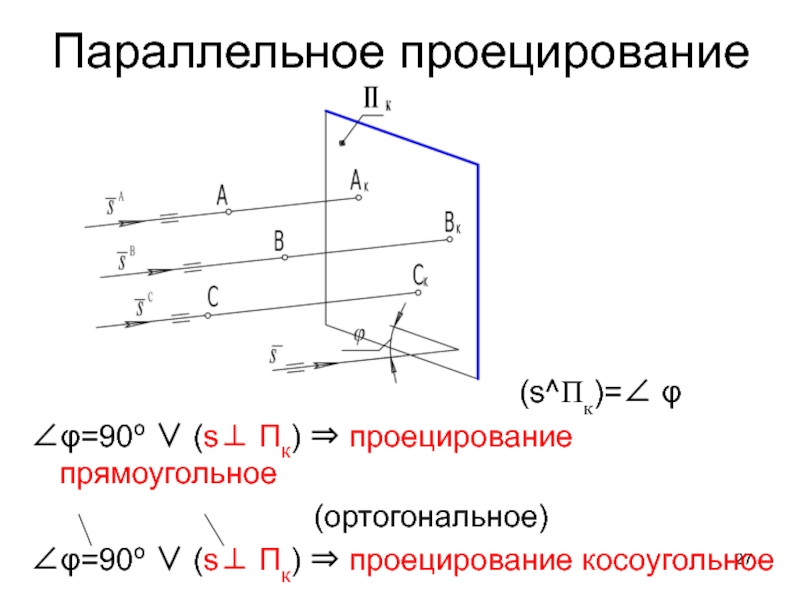
Слайд 27Параллельное проецирование
(s^Пк)= φ
φ=90º (s Пк) проецирование прямоугольное
(ортогональное)
φ=90º (s Пк) проецирование косоугольное
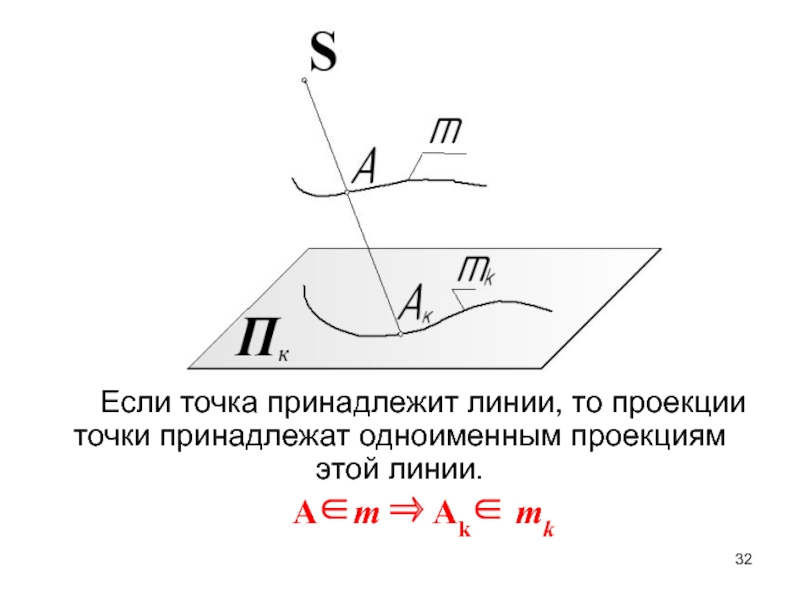
Слайд 32Если точка принадлежит линии, то проекции точки принадлежат одноименным проекциям
этой линии.
Am Ak mk
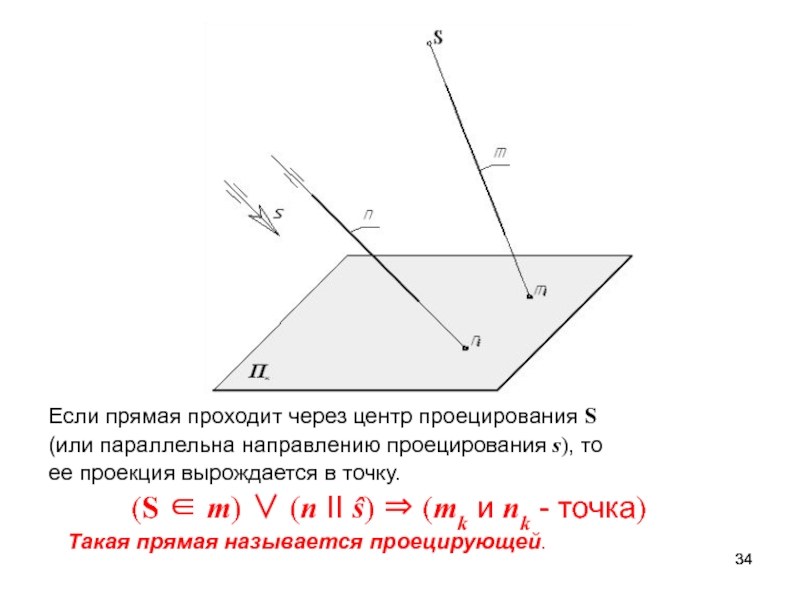
Слайд 34Если прямая проходит через центр проецирования S
(или параллельна направлению
проецирования s), то
ее проекция вырождается в точку.
(S m) (n II ŝ) (mk и nk - точка)
Такая прямая называется проецирующей.
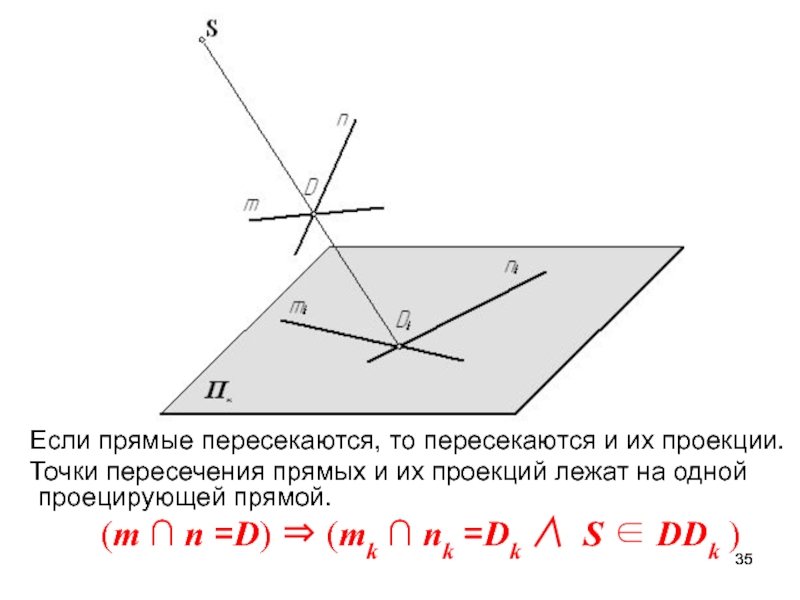
Слайд 35 Если прямые пересекаются, то пересекаются и их проекции.
Точки пересечения прямых и их проекций лежат на одной
проецирующей прямой.(m ∩ n =D) (mk ∩ nk =Dk S DDk )
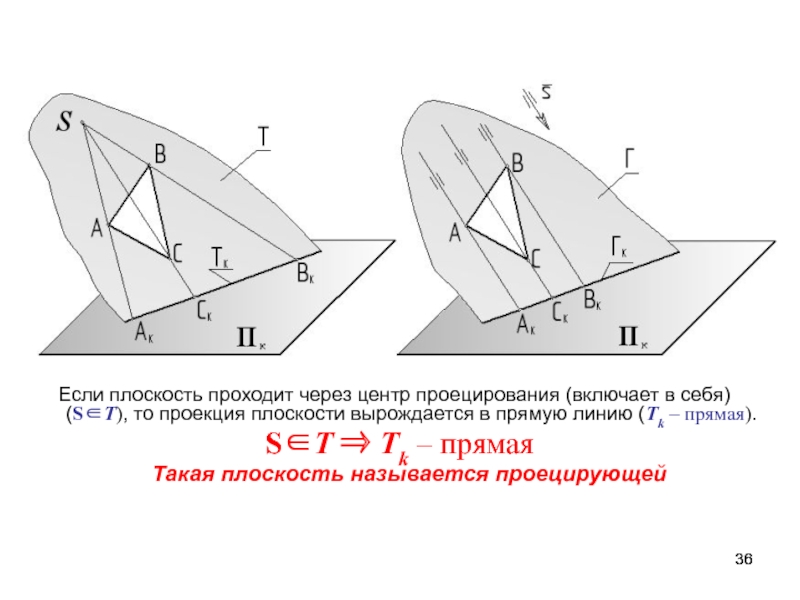
Слайд 36 Если плоскость проходит через центр проецирования (включает в
себя) (SТ), то проекция плоскости вырождается в прямую линию (Тk
– прямая).SТ Тk – прямая
Такая плоскость называется проецирующей
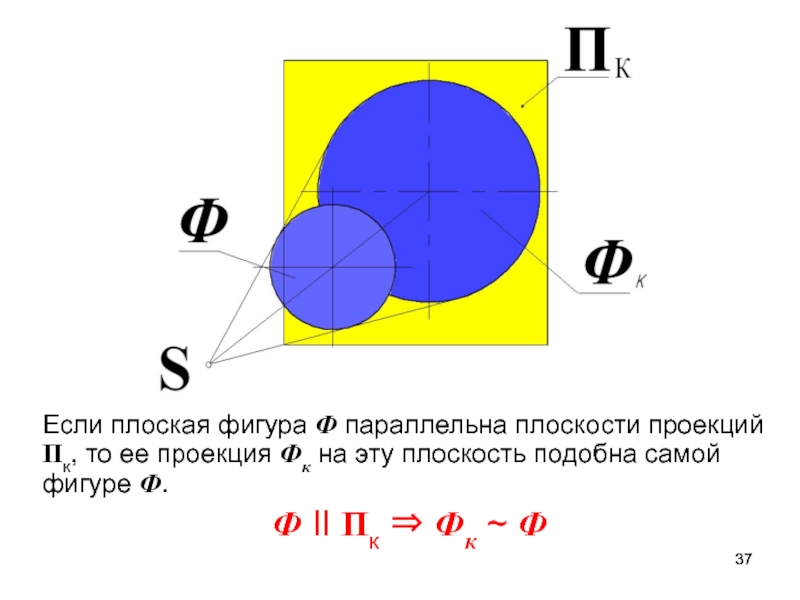
Слайд 37Если плоская фигура Ф параллельна плоскости проекций Пк, то ее
проекция Фк на эту плоскость подобна самой фигуре Ф.
Ф II
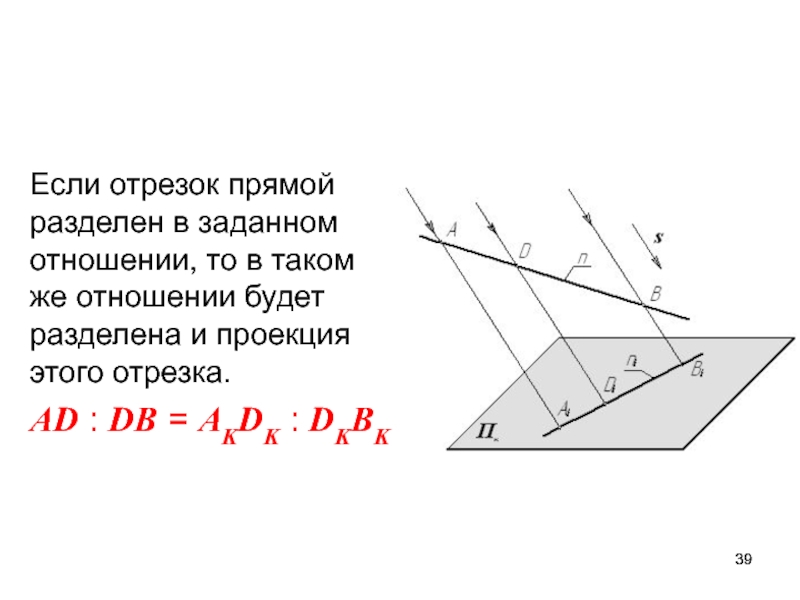
Пк Фк ~ Ф
Слайд 39Если отрезок прямой разделен в заданном отношении, то в таком
же отношении будет разделена и проекция этого отрезка.
AD : DB
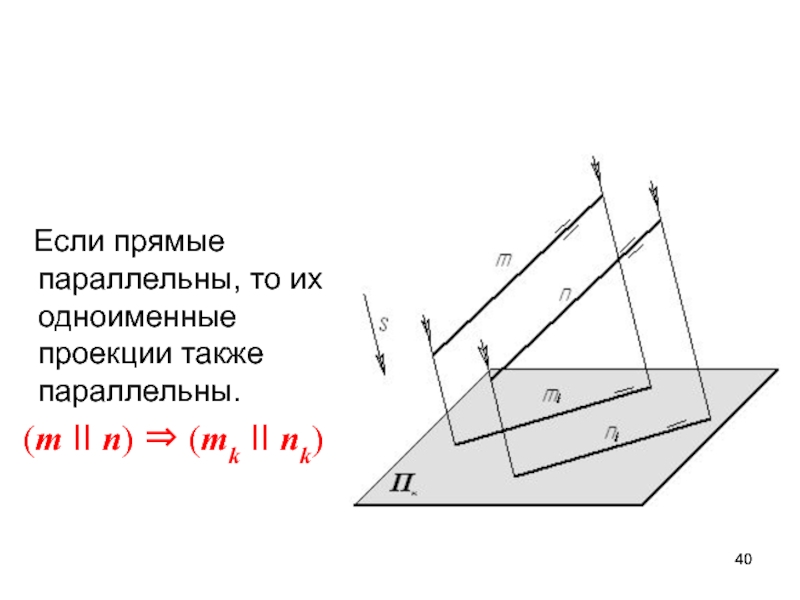
= AKDK : DKBK
Слайд 40 Если прямые параллельны, то их одноименные проекции также
параллельны.
(m II n) (mk II nk)
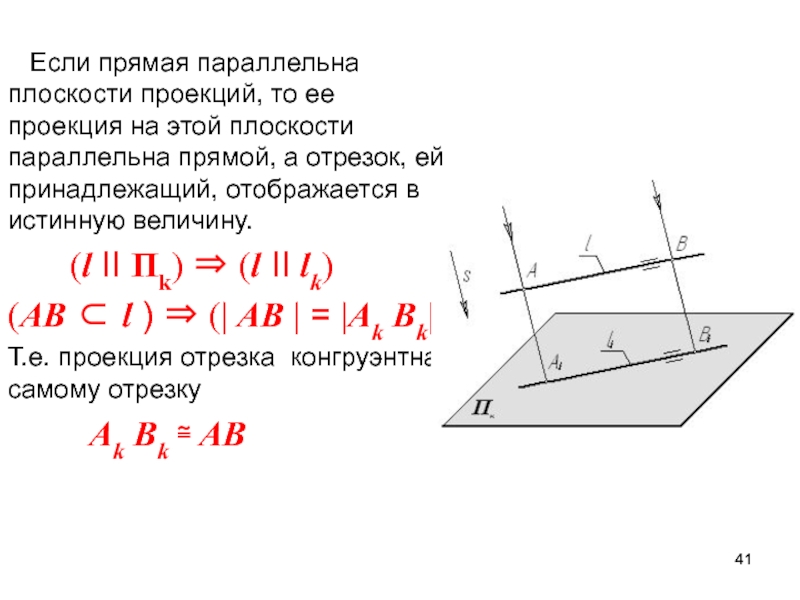
Слайд 41 Если прямая параллельна плоскости проекций, то ее проекция
на этой плоскости параллельна прямой, а отрезок, ей принадлежащий, отображается
в истинную величину.(l II Пk) (l II lk)
(AB l ) (| AB | = |Ak Bk|)
Т.е. проекция отрезка конгруэнтна самому отрезку
Ak Bk AB
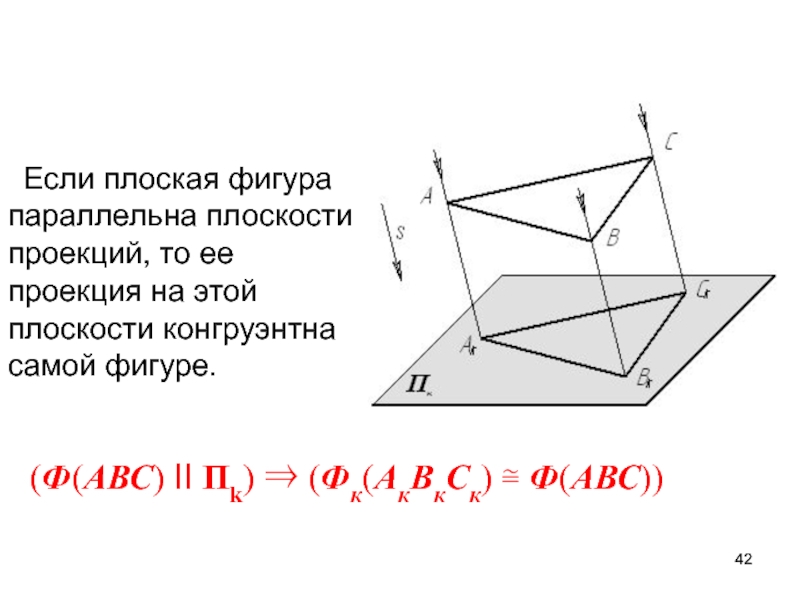
Слайд 42Если плоская фигура параллельна плоскости проекций, то ее проекция на
этой плоскости конгруэнтна самой фигуре.
(Ф(АВС) II Пk) (Фк(АкВкСк)
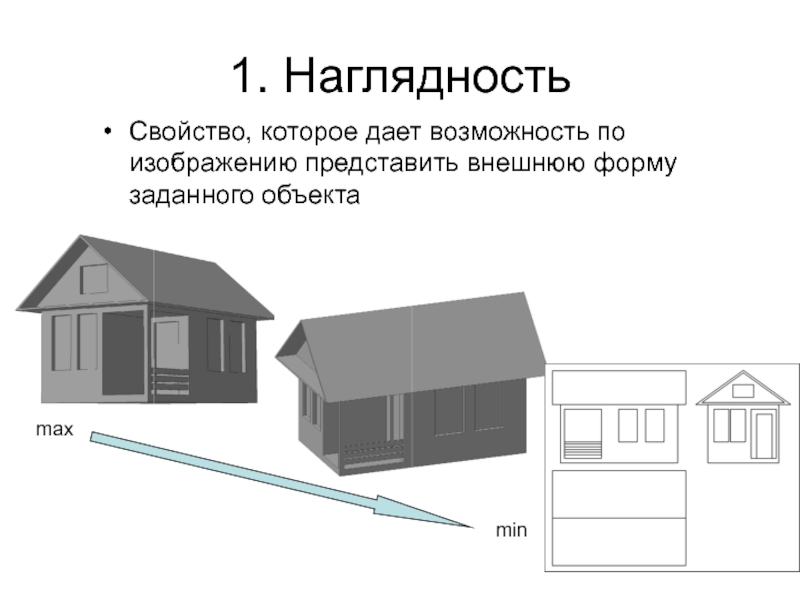
Ф(АВС))
Слайд 441. Наглядность
Свойство, которое дает возможность по изображению представить внешнюю форму
заданного объекта
max
min
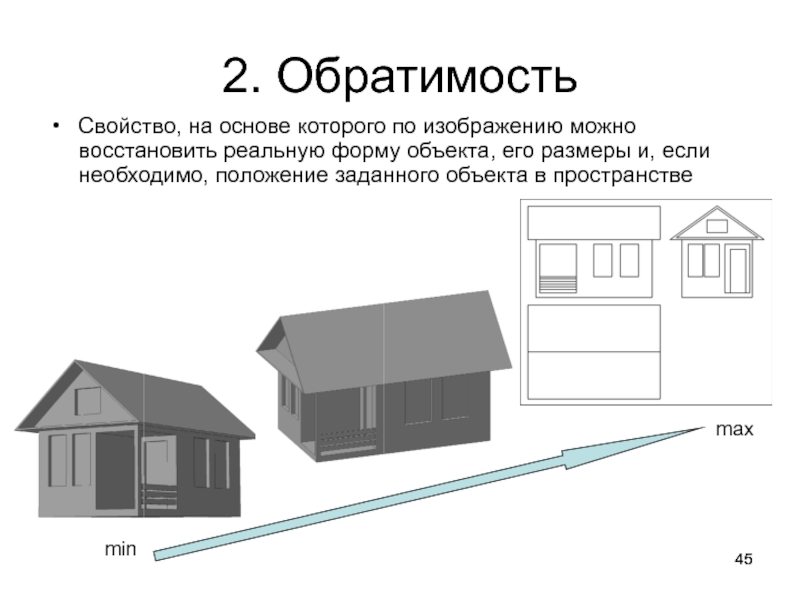
Слайд 452. Обратимость
Свойство, на основе которого по изображению можно восстановить реальную
форму объекта, его размеры и, если необходимо, положение заданного объекта
в пространствеmin
max
Слайд 47Выбор того или иного вида проекции определяется функциональным назначением получаемого
изображения.
Для презентаций определяющим свойством является наглядность изображения (перспективная или аксонометрическая
проекция).Для разработки технологического процесса изготовления (строительства) объекта определяющим является обратимость изображения (ортогональные проекции).
Выводы
Слайд 50 Спроецируем точку А на плоскость проекций Пк по
направлению s.
Полученная проекция Ак точки А не дает возможности точно
определить положение самой точки А в пространстве, так как проекции Ак соответствует все множество точек, принадлежащих проецирующей прямой, проходящей через точку АОдна проекция точки без дополнительных условий
однозначно не определяет ее положение в пространстве
.
.
Слайд 51Введем пространственную ортогональную систему координат Оxyz с условием, что координатная
плоскость хОу будет параллельна плоскости проекций П1. “Привяжем” точку А
к выбранной системе координат.
Слайд 52 Ортогонально спроецируем систему координат Oxyz и связанную с
ней точку А на плоскость проекций П1.
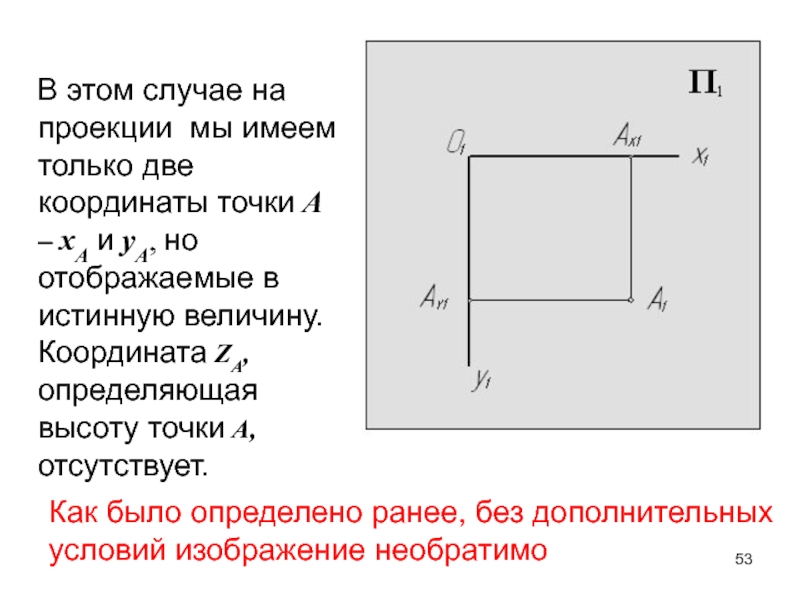
Слайд 53 В этом случае на проекции мы имеем только
две координаты точки А – xA и yA, но отображаемые
в истинную величину. Координата ZA, определяющая высоту точки А, отсутствует.Как было определено ранее, без дополнительных
условий изображение необратимо
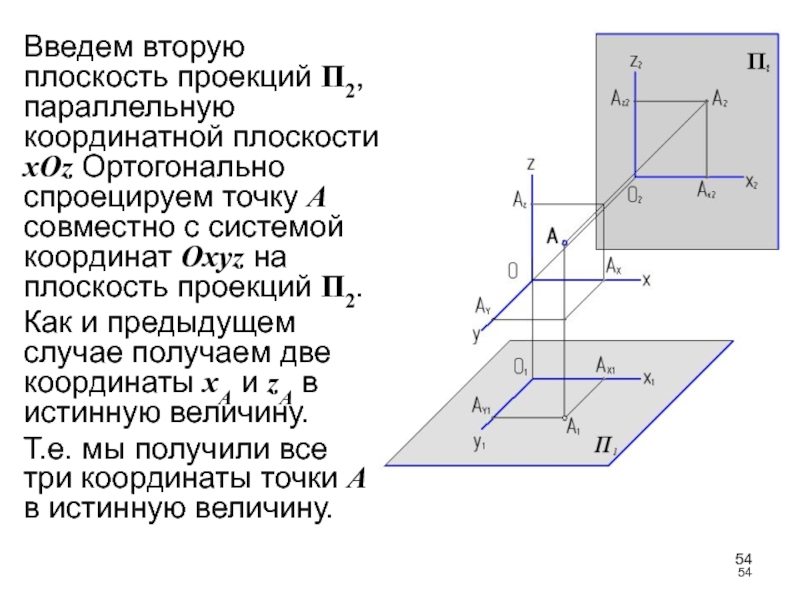
Слайд 54Введем вторую плоскость проекций П2, параллельную координатной плоскости xOz Ортогонально
спроецируем точку А совместно с системой координат Oxyz на плоскость
проекций П2.Как и предыдущем случае получаем две координаты xA и zA в истинную величину.
Т.е. мы получили все три координаты точки А в истинную величину.
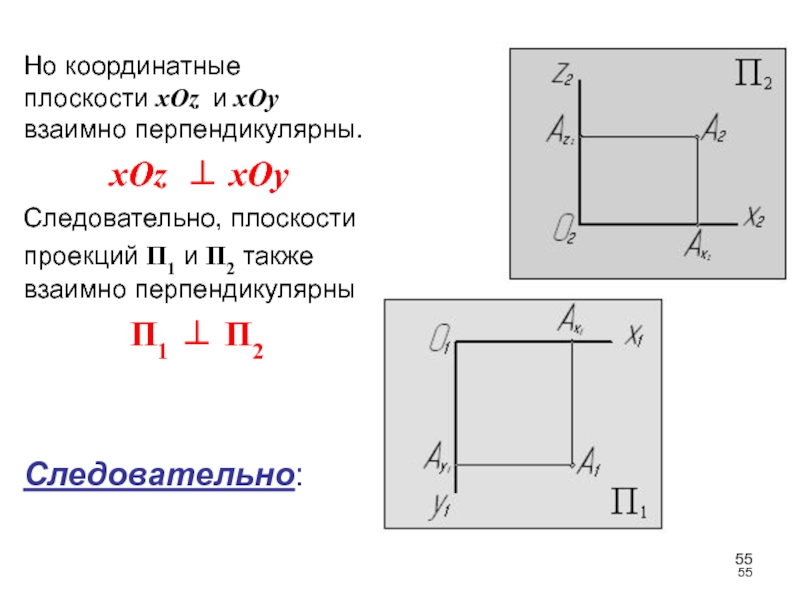
Слайд 55Но координатные плоскости xOz и xOy взаимно перпендикулярны.
xOz xOy
Следовательно, плоскости проекций П1
и П2 также взаимно перпендикулярныП1 П2
Следовательно:
Слайд 56 Ортогональные проекции точки на две взаимно перпендикулярные плоскости
проекций однозначно определяют положение точки в пространстве и делают изображения
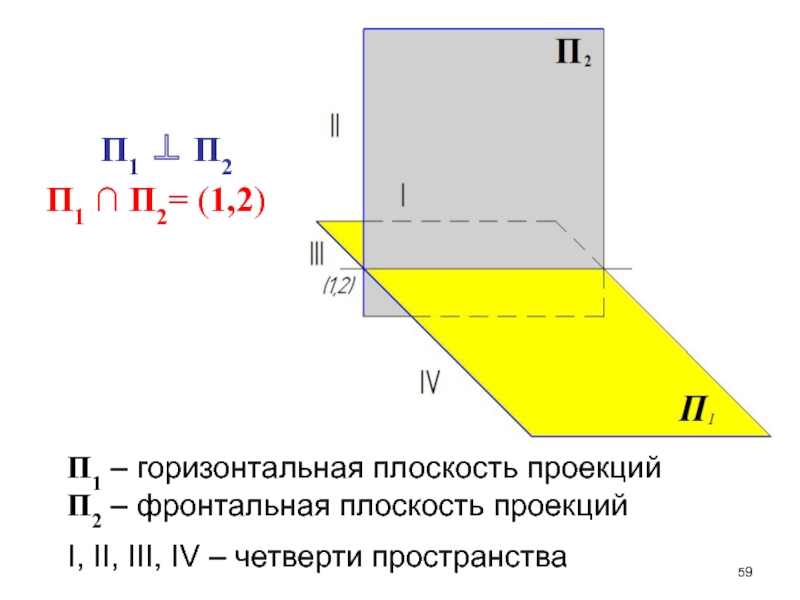
обратимыми.
Слайд 59 П1 П2
П1 ∩ П2= (1,2)
П1
– горизонтальная плоскость проекций
П2 – фронтальная плоскость проекций
I, II, III,
IV – четверти пространства
Слайд 60 Пространственная система координат совмещается с плоскостями проекций так,
чтобы
xOz П2 ,
xOy П1 ,
x (1,2)
Слайд 61 Для получения плоскостного чертежа горизонтальную плоскость проекций П1
поворачивают вокруг линии пересечения (1,2) до совмещения с плоскостью П2.
Слайд 63 Так как плоскости проекций бесконечны, то их границы не
оказывают.
Координатные оси y и z также не показывают.
В дальнейшем, когда не требуется знать положение объекта в пространстве относительно системы координат Oxyz, ось х1,2 также может не изображать-ся. Получаем безосную систему.
Слайд 65П3∩П1=(1,3), (1,3)y y1,3
П3∩П2=(2,3), (2,3)z z2,3
П2∩П1=(1,2), (1,2)x x1,2
Вводится
третья плоскость проекций
П3 – профильная
П3 ≡ yOz
П3
П1 и П3 П2;Пространство разделено на 8 частей - октантов
Слайд 66 Для перехода от трехмерного изображения к плоскостному-
двумерному выполняют следующие действия:
Положение фронтальной плоскости проекций П2 не изменяют;
горизонтальную
плоскость проекций П1 поворачивают вокруг оси x1,2 до совмещения с фронтальной плоскостью проекций П2;профильную плоскость проекций П3 поворачивают вокруг оси z2,3 также до совмещения с фронтальной плоскостью проекций П2.
Слайд 71 Горизонтальная и фронтальная проекции точки располагаются на одной
прямой, перпендикулярной оси x1,2
А1А2 х1,2Расстояние от оси x1,2 до горизонтальной проекции точки определяет расстояние от самой точки до фронтальной плоскости проекций.
(х1,2 , А1) = (А, П2) - глубина
Расстояние от оси x1,2 до фронтальной проекции точки определяет расстояние от самой точки до горизонтальной плоскости проекций.
(х1,2 , А2) = (А, П1) - высота
Слайд 72Абсолютные и относительные координаты точки
zA, zB, zC, yA, yB, yC
– абсолютные координаты;
z, y – относительные координаты (приращения).
Слайд 73Безосный эпюр
Точка В выше точки А;
Точка С перед точкой А;
Точка
D ниже точки А и за точкой А;
Точка Е выше
точки А и перед точкой А;Точка F ниже точки А и перед точкой А;
Точка М выше точки А и за точкой А.
Слайд 75Точка в первом октанте
Наглядное изображение
Эпюр
(A,П1)=(А2,х1,2)=zА
(A,П2)=(А1,х1,2)=yА абсолютные координаты точки
(A,П3)=(А2,z2,3)=хА
Слайд 76Условия, которым должен удовлетворять эпюр точки, расположенной в любой части
пространства, в системе трех ортогональных плоскостей проекций:
А1А2 х1,2
А2А3
z2,3(A1,x1,2) = (A3,z2,3)
