Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гипотеза де Бройля
Содержание
- 1. Гипотеза де Бройля
- 2. Слайд 2
- 3. Слайд 3
- 4. § 9.2. Уравнение Шредингера. Волновая функция.плотность вероятности:условие нормировки вероятности:
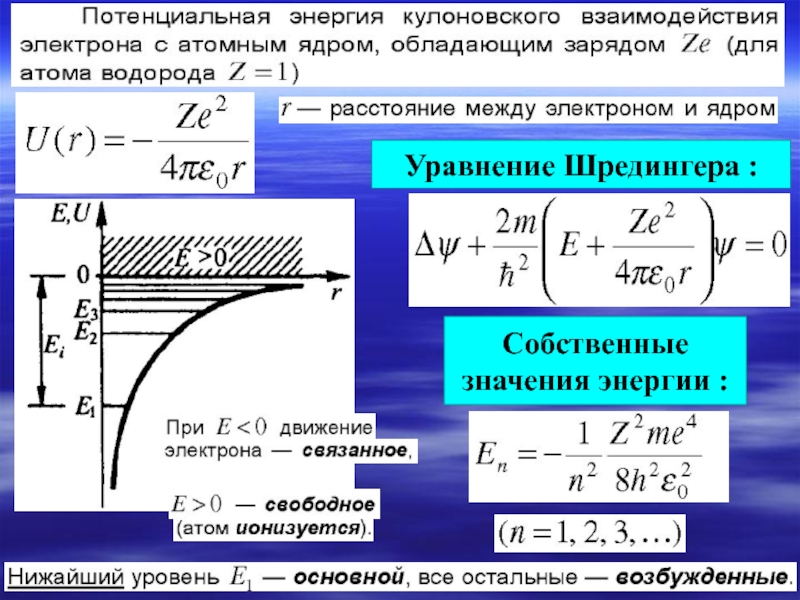
- 5. Уравнение Шредингера для стационарных состояний.
- 6. Уравнение Шредингера :Собственные значения энергии :
- 7. § 9.3. Квантовые числа.
- 8. Эффект Зеемана – расщепление в магнитном поле
- 9. Квантовые числа n и l характеризуют размер
- 10. Правила отбора: Для электрона существуют такие переходы,
- 11. § 9.4. Спин электрона.Штерн и Герлах (1922
- 12. Состояние электрона в атоме определяется набором четырех
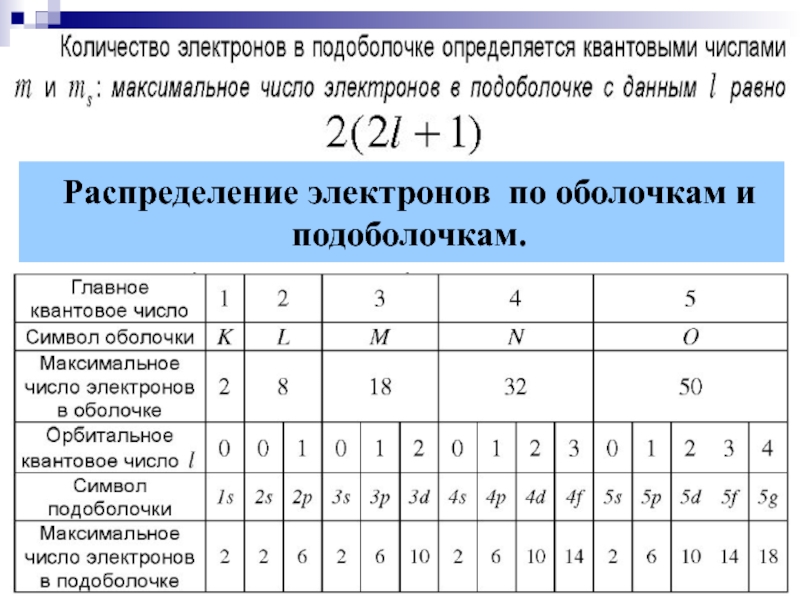
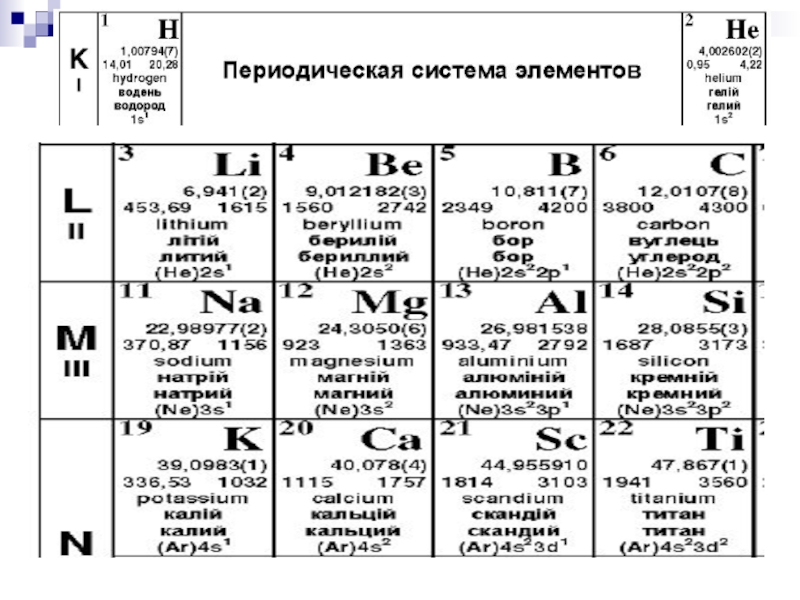
- 13. § 9.5. Распределение электронов в атоме по
- 14. Распределение электронов по оболочкам и подоболочкам.
- 15. Слайд 15
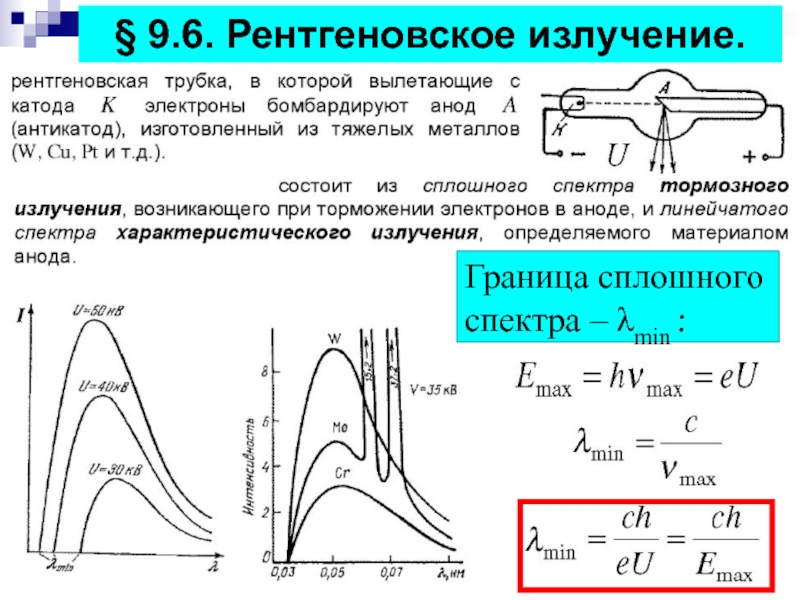
- 16. § 9.6. Рентгеновское излучение.Граница сплошного спектра – λmin :
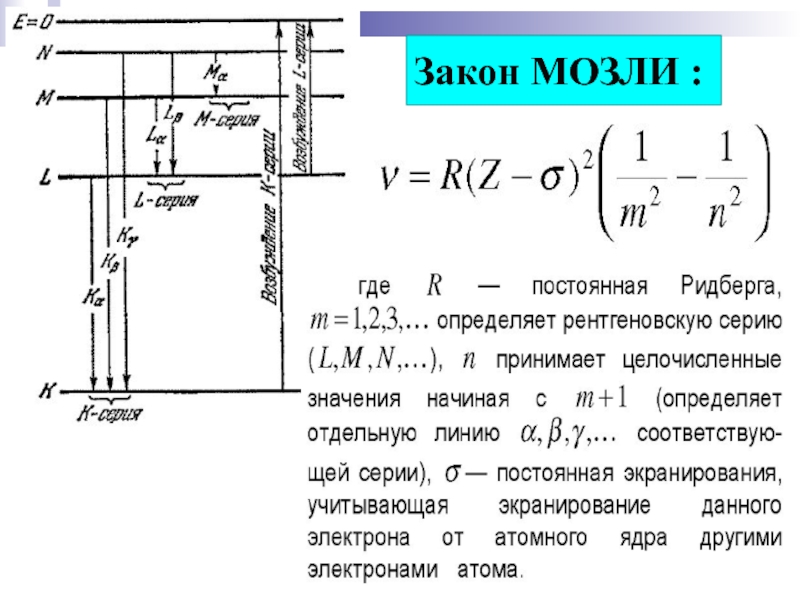
- 17. Закон МОЗЛИ :
- 18. § 9.7. Поглощение. Спонтанное и вынужденное излучение.
- 19. § 9.8. ЛАЗЕРЫ.
- 20. Скачать презентанцию
§ 9.2. Уравнение Шредингера. Волновая функция.плотность вероятности:условие нормировки вероятности:
Слайды и текст этой презентации
Слайд 4§ 9.2. Уравнение Шредингера.
Волновая функция.
плотность вероятности:
условие нормировки вероятности:
Слайд 8Эффект Зеемана – расщепление в магнитном поле уровня с главным
квантовым числом n на 2l+1 подуровней.
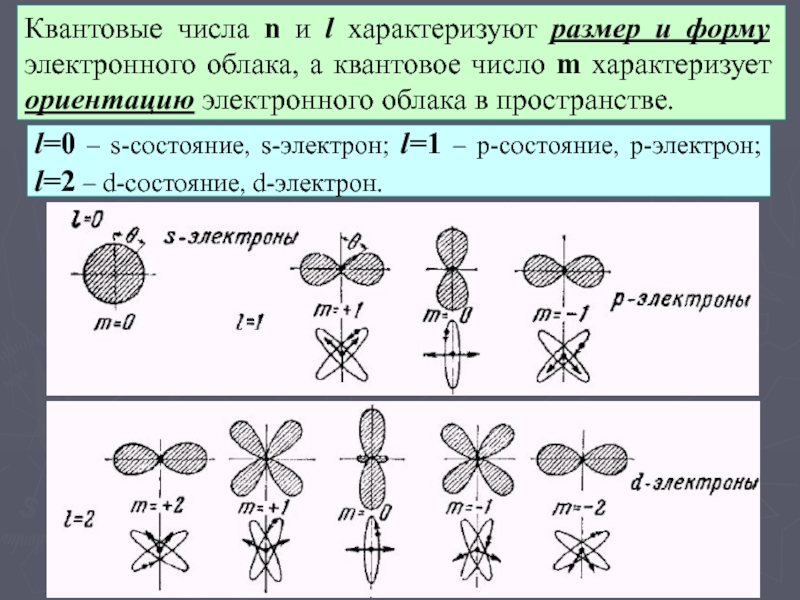
уровней энергии во внешнем электрическом поле.
Слайд 9Квантовые числа n и l характеризуют размер и форму электронного
облака, а квантовое число m характеризует ориентацию электронного облака в
пространстве.l=0 – s-состояние, s-электрон; l=1 – p-состояние, p-электрон;
l=2 – d-состояние, d-электрон.
Слайд 10Правила отбора:
Для электрона существуют такие переходы, для которых :
изменение Δl орбитального квантового числа l удовлетворяет условию
Δl =
± 1изменение Δm магнитного квантового числа удовлетворяет условию
Δm = 0, ± 1
серия Лаймана - np→1s (n=2,3…)
серия Бальмера - np→2s, ns→2p, nd→2p (n=3,4...)
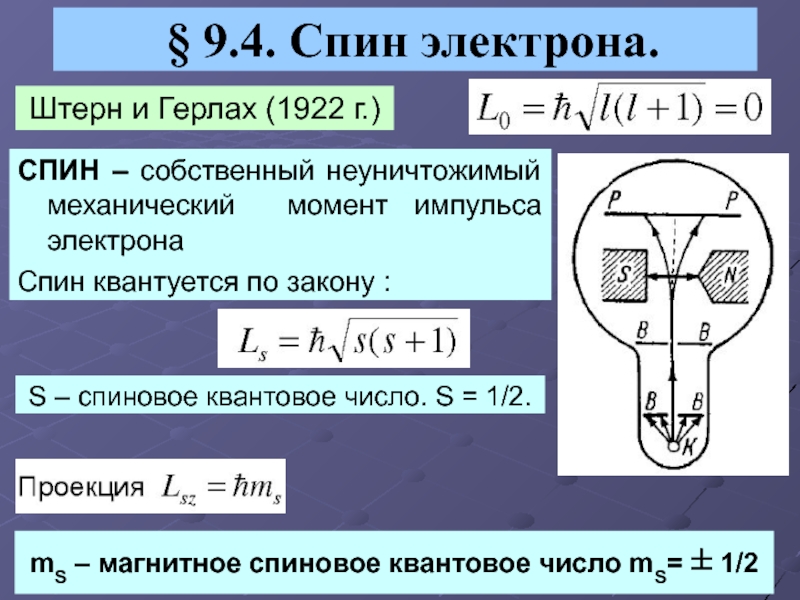
Слайд 11§ 9.4. Спин электрона.
Штерн и Герлах (1922 г.)
СПИН –
собственный неуничтожимый механический момент импульса электрона
Спин квантуется по закону :
S
– спиновое квантовое число. S = 1/2.mS – магнитное спиновое квантовое число mS= ± 1/2
Слайд 12Состояние электрона в атоме определяется набором четырех квантовых чисел:
главного
n (n=1, 2, 3, …)
орбитального l ( l=0, 1, 2,
3, n-1 )магнитного m ( m=0, ±1, ±2, ±3, ±l )
магнитного спинового ms ( m= ±1/2 )
Слайд 13§ 9.5. Распределение электронов в атоме по состояниям.
ПРИНЦИП ПАУЛИ: В
одном и том же атоме не может быть более одного
электрона с одинаковым набором четырех квантовых чисел n, l, m, ms .
