Слайд 2Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический процесс, созданный для
уточнения понятия алгоритма.
Это математический объект, а не физическая машина.
Предложена Аланом
Тьюрингом в 1936 году
Машина Тьюринга – это строгое математическое построение, математический аппарат, созданный для решения определённых задач.
Слайд 3Структура и описание машины Тьюринга
Машина Тьюринга состоит
из:
бесконечной ленты, разделенной на ячейки;
каретки (читающей и
записывающей головки);
программируемого автомата (программа в виде таблицы).
Автомат каждый раз “видит” только одну ячейку. В зависимости от того, какую букву он видит, а также в зависимости от своего состояния q автомат может выполнять следующие действия:
записать новую букву в обозреваемую ячейку;
выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться неподвижным;
перейти в новое состояние.
Слайд 41) Внешний алфавит
А = {a0, a1, …, an}
Элемент a0 называется
пустой символ или пустая буква (признак того, что ячейка пуста).
В
этом алфавите в виде слова кодируется исходный набор данных и результат работы алгоритма.
Устройство машины Тьюринга
Слайд 52) Внутренний алфавит
Q = {q0, q1, …, qm}, {П, Л,
С}
В любой момент времени машина Тьюринга находится в одном из
состояний q0, q1, …, qm
При этом: q1 - начальное состояние (машина начинает работу)
q0 - заключительное состояние (машина закончила работу)
Символы {П, Л, С} – символы сдвига (вправо, влево, на месте)
Устройство машины Тьюринга
Слайд 63) Внешняя память (лента)
Машина имеет ленту, разбитую на ячейки, в
каждую из которых может быть записана только одна буква
Устройство машины
Тьюринга
Слайд 73) Внешняя память (лента)
Устройство машины Тьюринга
Пустая клетка содержит a0.
В
каждый момент времени на ленте записано конечное число непустых букв
Лента
является конечной, но дополняется в любой момент ячейками слева и справа для записи новых непустых символов.
Это соответствует принципу абстракции потенциальной осуществимости
Слайд 84) Каретка (управляющая головка)
Каретка машины располагается над некоторой ячейкой ленты
– воспринимает символ, записанный в ячейке
В одном такте работы каретка
сдвигается на одну ячейку (вправо, влево) или остается на месте
Устройство машины Тьюринга
Слайд 95) Функциональная схема (программа)
Программа машины состоит из команд:
Устройство машины Тьюринга
Для
каждой пары (qi, aj) программа машины должна содержать одну команду
(детерминированная машина Тьюринга)
Слайд 10К началу работы машины на ленту подается исходный набор данных
в виде слова
Описание работы машины Тьюринга
Будем говорить, что непустое
слово в алфавите А\{a0}={a i,...,a n} воспринимается машиной в стандартном положении, если:
- оно задано в последовательных ячейках ленты,
- все другие ячейки пусты,
- машина обозревает крайнюю правую ячейку из тех, в которых записано слово
Слайд 11Описание работы машины Тьюринга
Стандартное положение называется начальным (заключительным), если машина,
воспринимающая слово в стандартном положении, находится в начальном состоянии q1
(стоп-состоянии q0)
Слайд 12Находясь в не заключительном состоянии, машина совершает шаг, который определяется
текущим состоянием qi и обозреваемым символом aj
Описание работы машины Тьюринга
Слайд 13Описание работы машины Тьюринга
В соответствии с командой qiaj qkal
Х выполняются следующие действия:
1) Содержимое обозреваемой ячейки aj стирается и
в нее записывается символ al (который может совпадать с aj)
2) Машина переходит в новое состояние qk (оно может совпадать с состоянием qi)
3) Каретка перемещается в соответствии с управляемым символом Х {П, Л, C}
Слайд 14При переходе машины в заключительное состояние q0 ее работа прекращается
На
ленте записан результат работы алгоритма – слово в алфавите
А\{a0}
Описание работы машины Тьюринга
Слайд 15Машинным словом (конфигурацией) машины Тьюринга называется слово вида 1qkal 2,
где 1 и 2 - слова в алфавите А.
Слайд 16Конфигурация 1qkal 2 интерпретируется следующим образом:
- машина находится в состоянии
qk
- каретка обозревает на ленте символ al
- 1 и
2 – это содержимое ленты до и после символа al
Слайд 17П р и м е р 1. Дана машина Тьюринга
с внешним алфавитом
А = {0,1} (здесь 0 - символ пустой
ячейки), алфавитом внутренних
Применение машин Тьюринга к словам
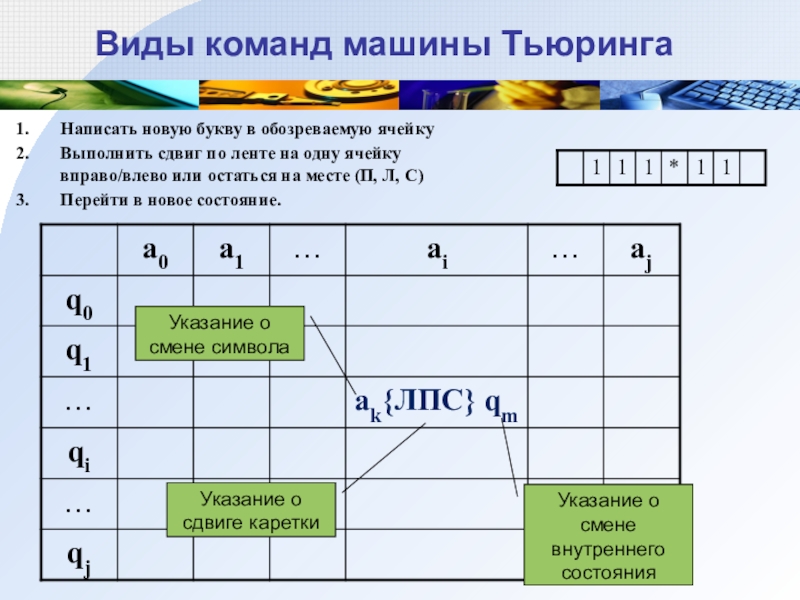
Слайд 18Виды команд машины Тьюринга
Написать новую букву в обозреваемую ячейку
Выполнить сдвиг
по ленте на одну ячейку
вправо/влево или остаться на месте
(П, Л, C)
Перейти в новое состояние.
Указание о смене символа
Указание о сдвиге каретки
Указание о смене внутреннего состояния
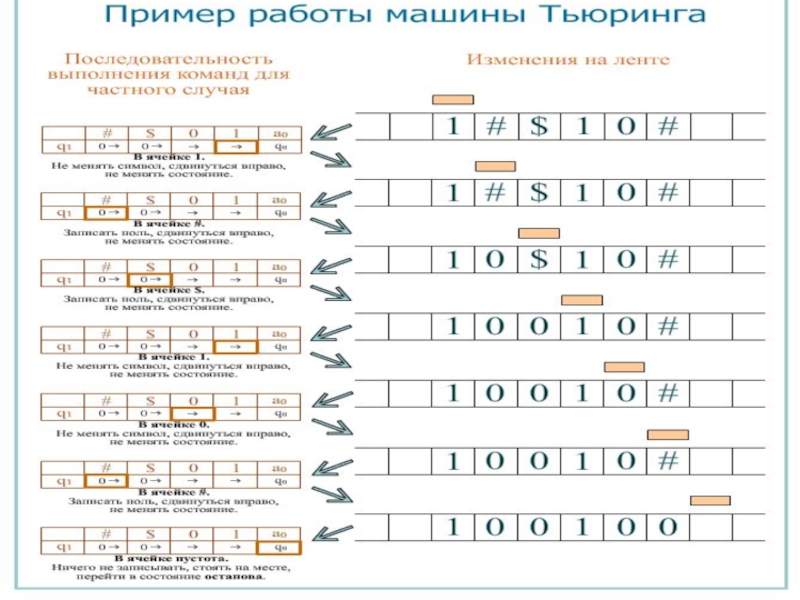
Слайд 20Пример
Дана машина Тьюринга с внешним алфавитом А = {a0, 1,
* }, алфавитом внутренних состояний Q = {q0, q1, q2,
q3}, и следующей функциональной схемой:
Применить машину Тьюринга к слову =11*1, начиная со стандартного начального положения
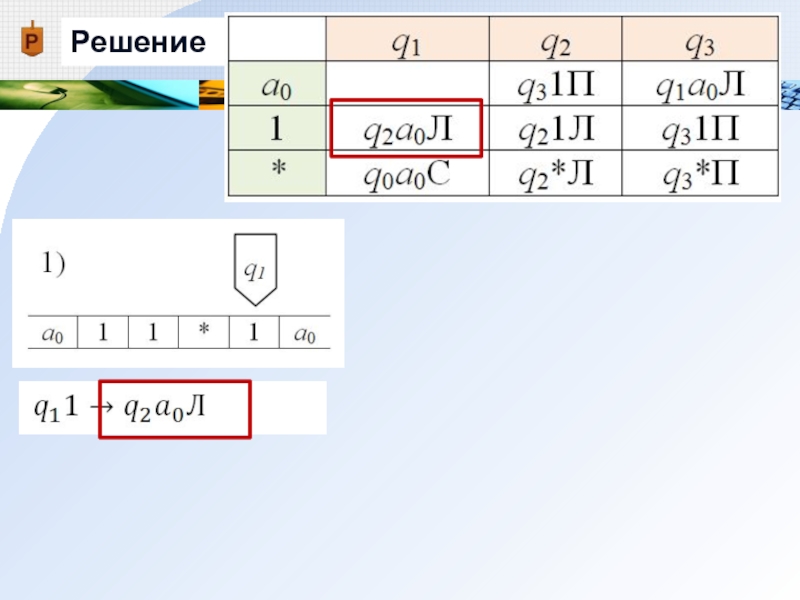
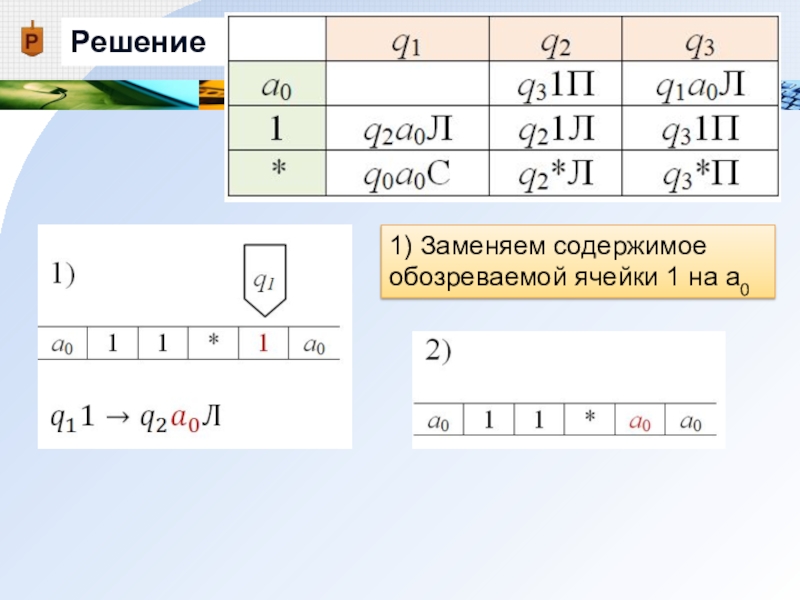
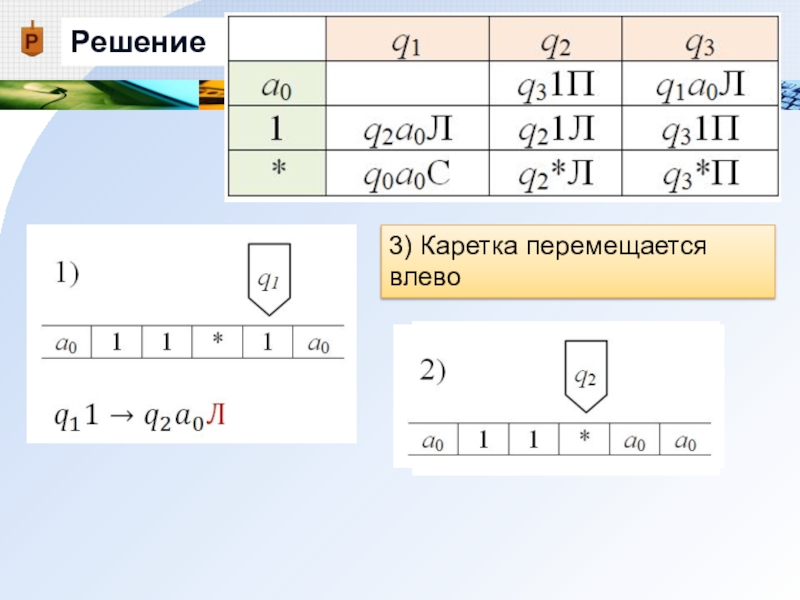
Слайд 22Решение
1) Заменяем содержимое обозреваемой ячейки 1 на а0
Слайд 23Решение
2) Машина переходит в новое состояние q2
Слайд 24Решение
3) Каретка перемещается влево
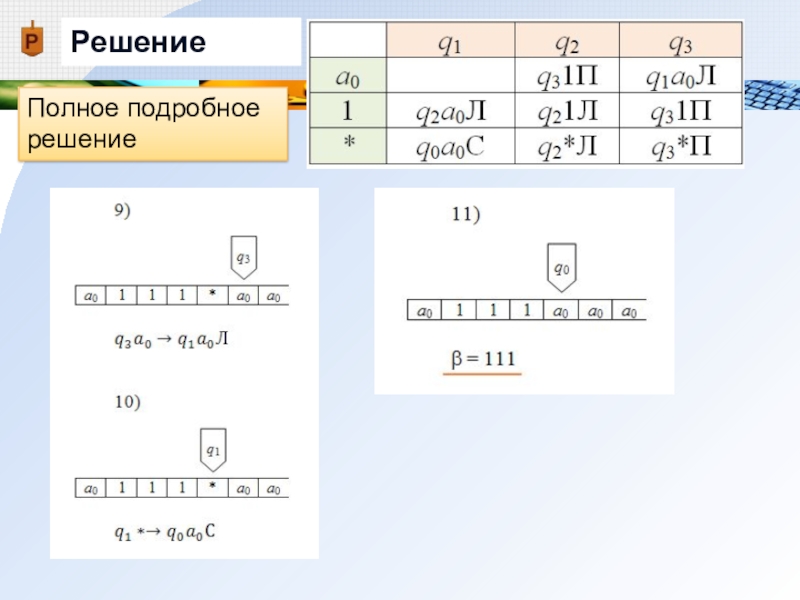
Слайд 28Решение
Решение, записанное с помощью конфигураций (в строчку)
Слайд 30Люди могут вести себя по-разному в одинаковых ситуациях, и этим
они принципиально отличаются от машин.
Слайд 40Определение
Пусть заданы машины Тьюринга
имеющие общий внешний алфавит
и алфавиты внутренних состояний
соответственно.
Композицией (или произведением) машины на машину называется новая машина
(которая обозначается ) с тем
же внешним алфавитом ,
алфавитом внутренних состояний
и программой, получающейся следующим образом.
Композиция машин Тьюринга
Слайд 46По исходному алгоритму переработки слов можно построить алгоритм для вычисления
соответствующей функции;
в этом случае
такие функции называются алгоритмически (или
эффективно) вычислимыми.
Возникает вопрос о соотношении между классом
алгоритмически вычислимых функций и классом функций, вычислимых на машинах Тьюринга.
Совпадают ли эти классы?
Слайд 47Вычислимость функций на машине Тьюринга
Определение
Функция называется вычислимой по Тьюрингу, или
вычислимой на машине Тьюринга, если существует машина Тьюринга, вычисляющая её,
т.е. такая машина Тьюринга, которая вычисляет
её значения для тех наборов значений аргументов, для которых функция определена, и работающая вечно, если функция для данного набора значений аргументов не определена.
Слайд 48Остаётся договориться о некоторых условностях
Во-первых,
речь идёт о функциях
(или возможно о частичных функциях, т.е. не всюду определённых), заданных
на множестве натуральных чисел и принимающих также натуральные значения.
Во-вторых,
нужно условиться:
как записывать на ленте машины Тьюринга значения
аргументов функции
из какого положения начинать переработку исходного слова
в каком положении получать значение функции.
Слайд 49Это можно делать следующим образом: Значения
аргументов будем
располагать на ленте в
виде следующего слова:
Слайд 50Начинать переработку данного слова будем из стандартного начального положения
Если функция
определена на данном наборе значений аргументов, то в результате на ленте должно быть записано подряд единиц;
в противном случае машина должна
работать бесконечно.
При выполнении всех перечисленных условий
будем говорить, что машина Тьюринга вычисляет данную функцию.
Таким образом, сформулированное определение становится абсолютно строгим
Слайд 51Правильная вычислимость функций на машине Тьюринга
Определение
Будем говорить, что машина
Тьюринга
правильно вычисляет функцию
если начальное слово
она переводит в слово и
при этом в процессе работы не пристраивает к начальному слову новых ячеек на ленте ни слева, ни справа.
Если же функция не определена на данном наборе значений аргументов, то, начав работать из указанного положения, она никогда в процессе работы не будет надстраивать ленту слева.
Слайд 52Тезис Тьюринга
(основная гипотеза теории алгоритмов)