Слайд 1Гипотезы, переменные, валидность, данные
Введение в статистику, лекция 1.
Слайд 2Как начинается исследование?
Сначала вы наблюдаете то, что вы хотите понять.
Потом
вы придумываете некоторые объяснения того, что вы хотите понять. Эти
объяснения в статистике называются теорией.
Теория позволяет вам сделать некоторые предположения о зависимостях между вашими наблюдениями. Такие предположения называются гипотезами.
Чтобы проверить гипотезы, вам нужны данные. Вы их собираете.
После того, как вы их собрали, вы их анализируете.
Анализ данных либо подтверждает теорию, либо ее уточняет.
Слайд 3Что такое валидное исследование?
Валидное исследование спланировано так, чтобы исключить альтернативные
объяснения наблюдаемого явления.
Условия валидности (условия для установления причинно-следственной зависимости
от явления А к явлению В):
Во-первых, А должно предшествовать по времени В; это хронологическая валидность.
Во-вторых, должна существовать статистическая зависимость между А и В; т.е. должно быть установлено, что А сопутствует В. Это – валидность статистического вывода.
В третьих, не должно быть альтернатив причине появления В помимо А. Это условие называется внутренней валидностью.
Существует и конструктная валидность, которая связана с верным выбором теории.
Наконец, в-пятых, существует внешняя валидность – возможность обобщения результатов для различных периодов времени, условий и групп.
Слайд 4Зависимые и независимые переменные
Для того, чтобы проверить гипотезы, мы должны
измерить переменные.
Переменные меняются (варьируются) между людьми (IQ, рост, вес), от
условий (работающие или безработные), во времени (настроение, доход, количество детей).
Большинство гипотез может быть выражено в терминах двух переменных: причина и следствие.
Те переменные о которых мы думаем, что они причина, называются независимыми.
Те переменные, которые мы воспринимаем как следствие – называются зависимыми.
Слайд 5Уровни измерения
Переменные бывают дискретные и непрерывные. В статистике дискретные переменные
называют категориальными.
Категориальные переменные бывают:
Биноминальными
Номинальными
Порядковыми
Непрерывные переменные бывают:
Метрические
Интервальные
Слайд 6Частотное распределение
После того, как вы собрали данные, полезно для каждой
переменной посчитать, сколько раз встречается каждое ее значение и построить
график.
Такие расчеты называются частотным распределением, а график – гистограммой.
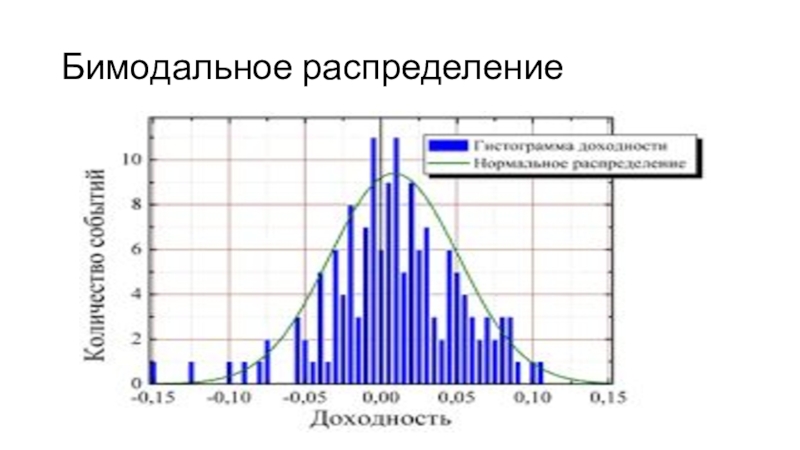
В идеальном мире наше распределение должно быть нормальным.
Потому что все случайные переменные распределены нормально.
Слайд 7Гистограмма и нормальное распределение
Слайд 8Центральная тенденция
После того, как мы сделали частотное распределение, нам нужно
найти его центр, который называют центральной тенденцией.
Есть три основных измерения
центральной тенденции: среднее, мода и медиана.
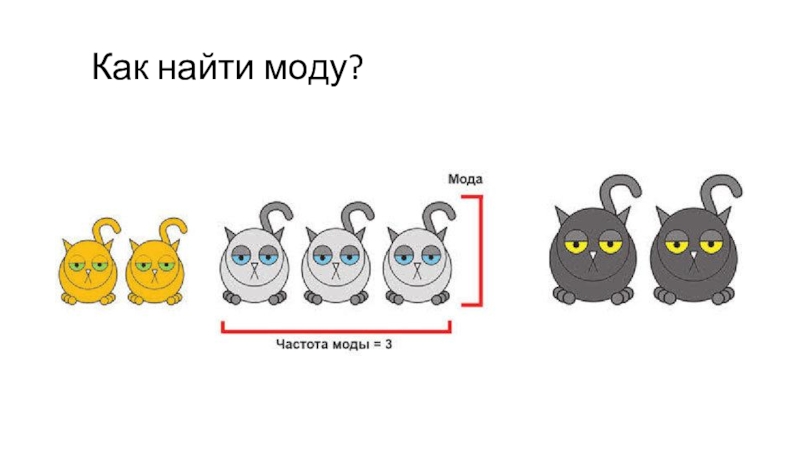
Слайд 9Мода
Мода – это значение, которое встречается чаще всего.
Ее легко
увидеть на графике.
Ее легко вычислить: надо посчитать сколько раз встречается
то или иное значение переменной и выбрать то, которое встречается чаще.
Слайд 14Медиана
Еще один способ определить центр распределения – это посчитать медиану.
Медиана
– это значение, которое делит нашу выборку пополам, т.е половина
выборки имеет значение этого параметра ниже, чем медиана, а вторая половина выборки – выше, чем медиана.
Пример: количество друзей в Facebook: 108, 103, 252, 121, 93, 57, 40, 53, 22, 116, 98
Для того, чтобы посчитать медиану, надо расположить значения в порядке возрастания: 22, 40, 53, 57, 93, 98, 103, 108, 116, 121, 252
Затем найдем элемент выборки, который находится посередине: n=11, (n+1)/2=6
Значение 6-го элемента равно 98.
Медиана=98.
У номинальных переменных медианы нет!!! Они не числовые!!!!
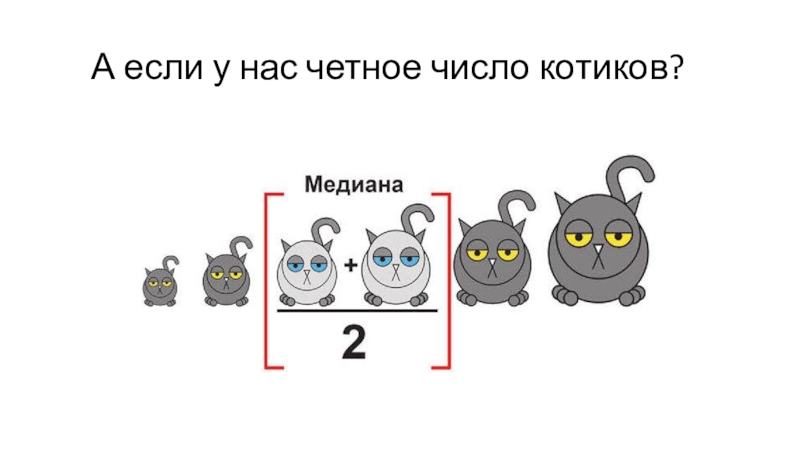
Слайд 16 А если у нас четное число котиков?
Слайд 17Среднее (Mean)
Среднее – это среднестатистическое значение нашего распределение (average)
Для того,
чтобы его вычислить надо сложить все значения нашего распределения и
поделить на размер выборки:
Σ(xi) = 22 + 40 + 53 + 57 + 93 + 98 + 103 + 108 + 116 + 121 + 252
= 1063
X̅=Σ(xi)/n=1063/11=96.64
Слайд 18 Почему среднее не всегда является лучшим показателем типичности?
Слайд 19Как корректировать данные при выбросах?
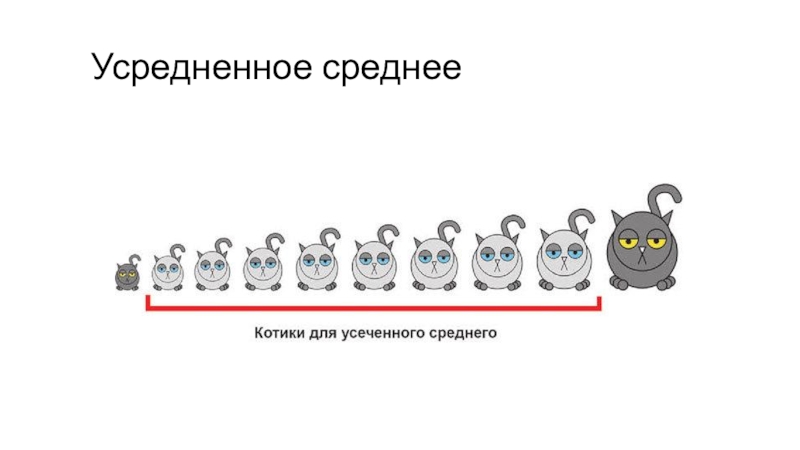
Надо убрать 5-10% самых больших и
самых маленьких значений, и посчитать среднее для оставшихся величин.
Такой
показатель называется усредненное среднее.
Слайд 21Меры разнообразия
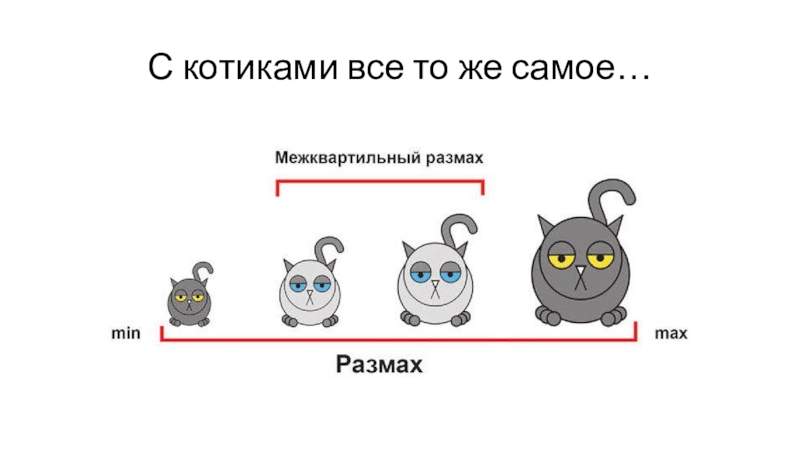
Межквартильный размах.
Размах – различие между самой большой и самой
маленькой величиной.
Если мы уберем 25% самых больших значений и самых
маленьких значений, то получим межквартильный размах.
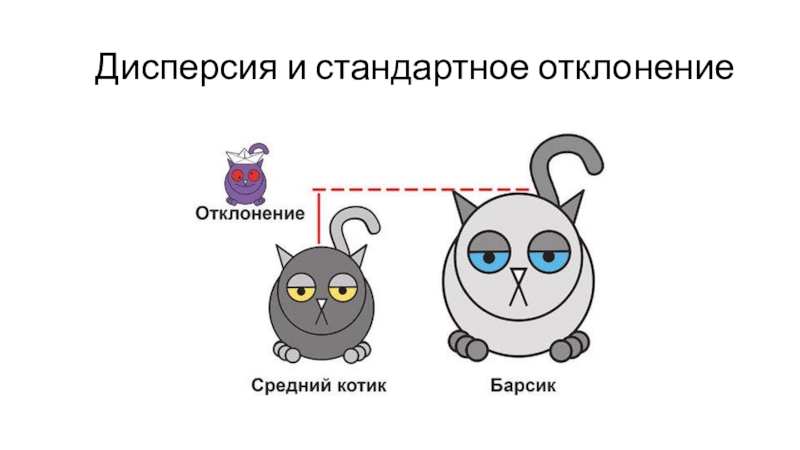
Слайд 23 Дисперсия и стандартное отклонение
Слайд 24Как посчитать дисперсию и стандартное отклонение?
Если взять и сложить все
отклонения от среднего, то получится 0, так как отклонения бывают
в разную сторону.
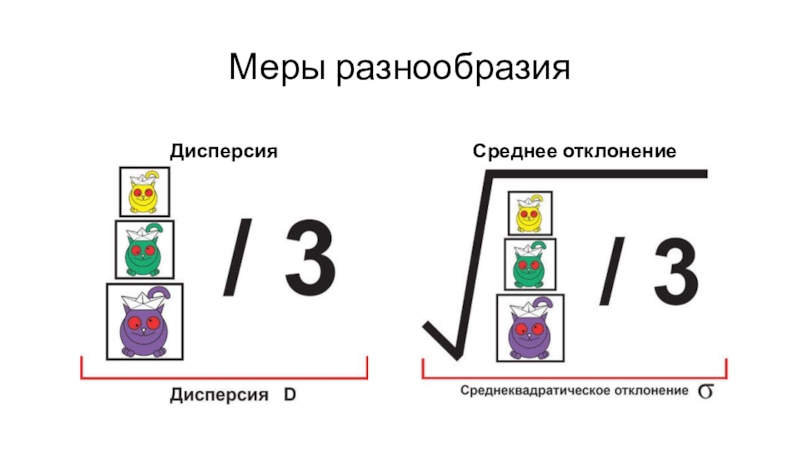
Поэтому отклонения от среднего надо возвести в квадрат, а потом уже сложить.
Полученную сумму надо разделить на общее количество наблюдений.
х2=(xi–x)2/N
(корень из х2 )- стандартное отклонение
Слайд 25Меры разнообразия
Дисперсия
Среднее отклонение
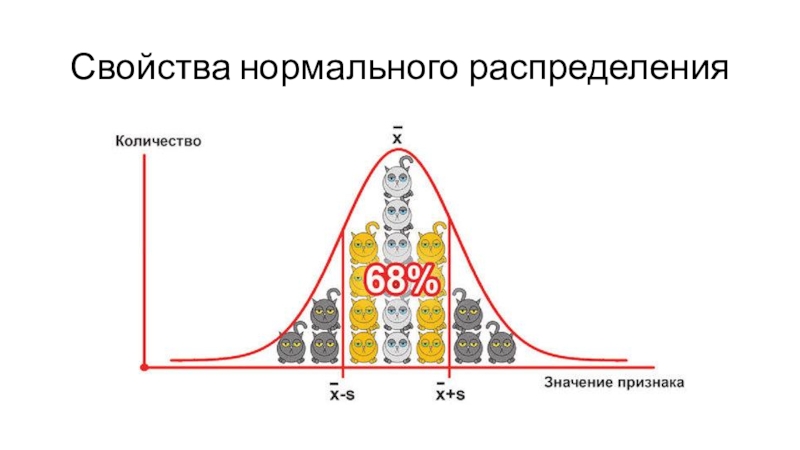
Слайд 28Свойства нормального распределения
Слайд 29Особенность нормального распределения
Особенностью нормального распределения является то, что 99,73% всех
случаев находятся в пределах трех стандартных отклонений от среднего значения.
В пределах двух стандартных отклонения находится 96% всех случаев.
95% всех случаев будут находиться в пределах 1,96 стандартных отклонений от средней.
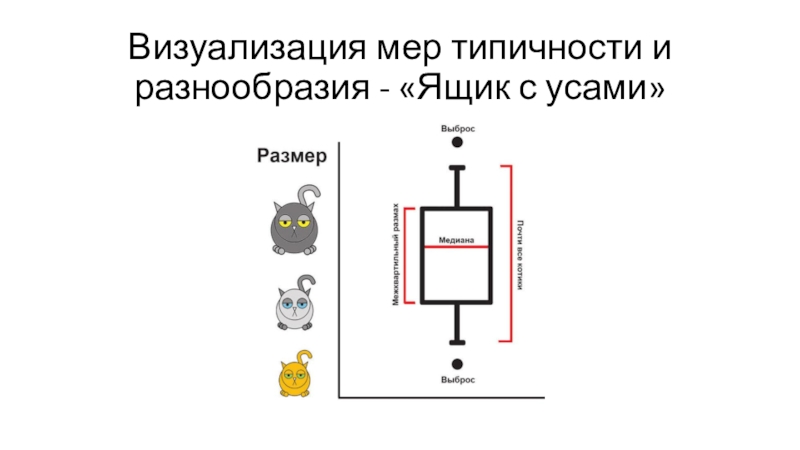
Слайд 30Визуализация мер типичности и разнообразия - «Ящик с усами»
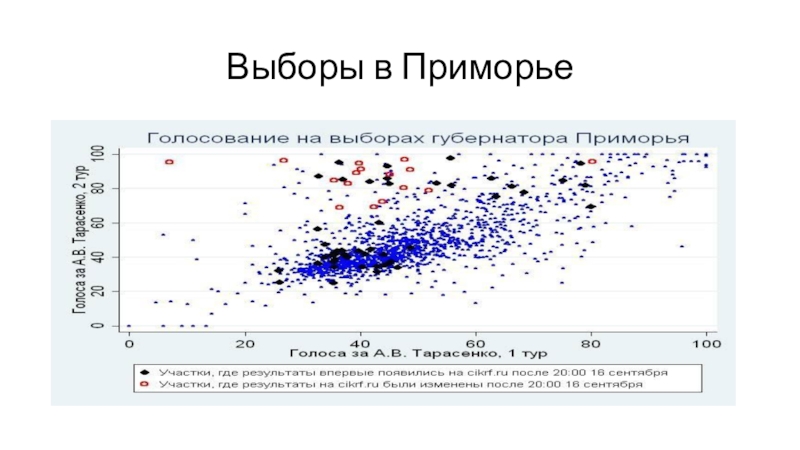
Слайд 31Явка и голосование за партию власти
Санкт-Петербург
Чечня
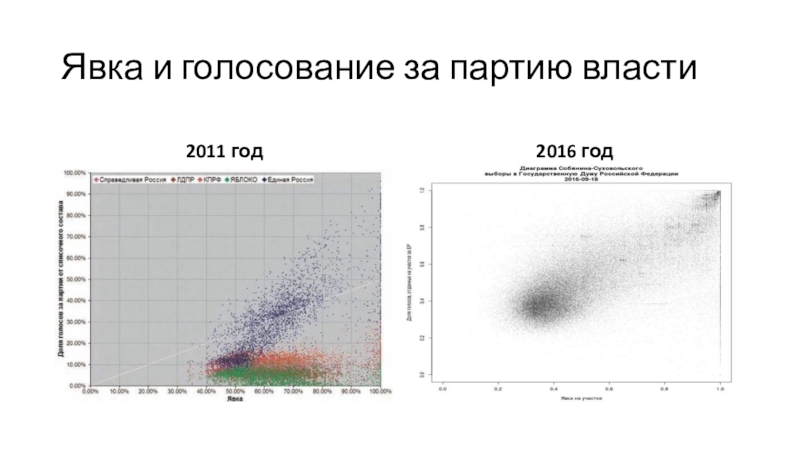
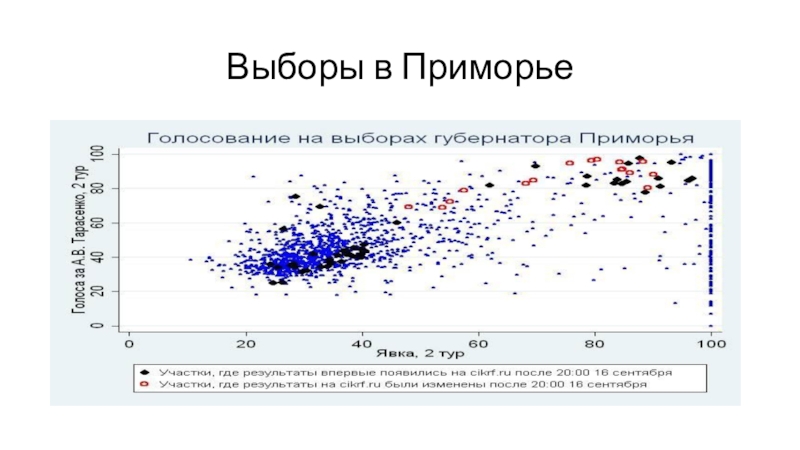
Слайд 32Явка и голосование за партию власти
2011 год
2016 год
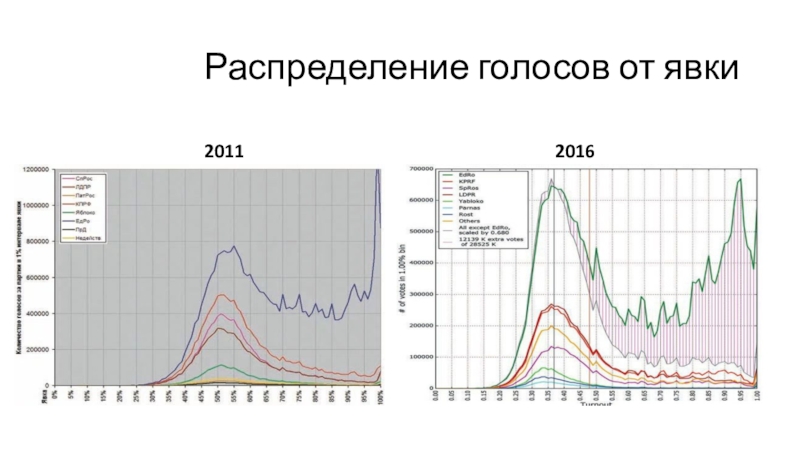
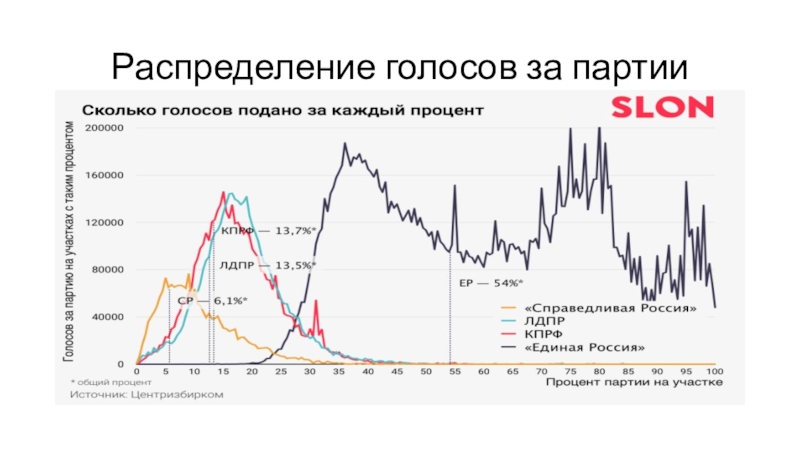
Слайд 35Распределение голосов от явки
2011
2016
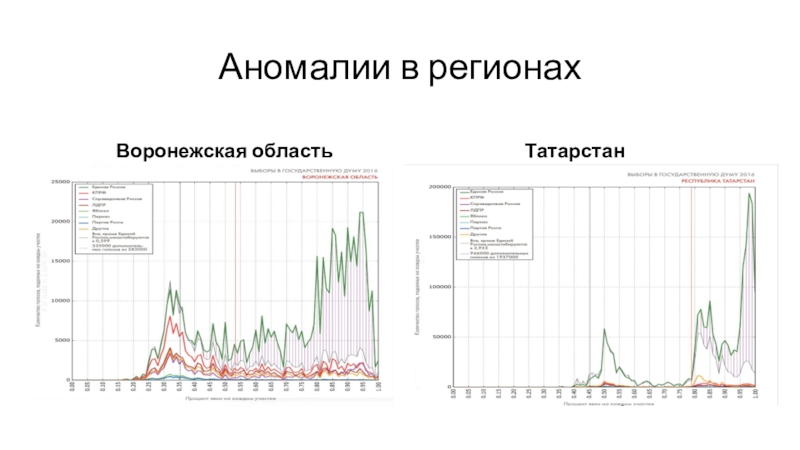
Слайд 36Аномалии в регионах
Воронежская область
Татарстан