ГЛАВА 17. АНАЛИТИЧЕСКОЕ (ПИСЬМЕННОЕ) СЧИСЛЕНИЕ КООРДИНАТ

АНАЛИТИЧЕСКОЕ (ПИСЬМЕННОЕ) СЧИСЛЕНИЕ КООРДИНАТ
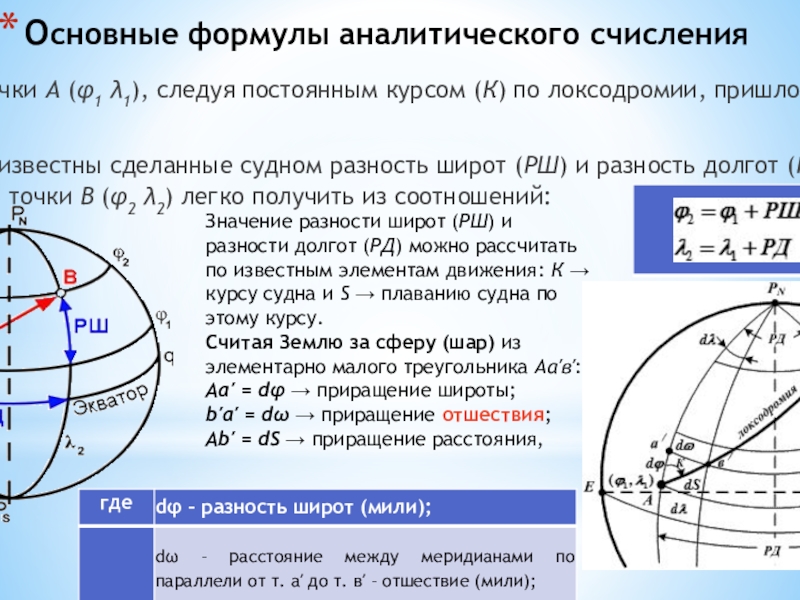
Аналитическое счисление – вычисление географических координат судна по

Аналитическое счисление производится по формулам и применяется при плавании судна вдали от берегов на океанских переходах, когда ведение графического счисления становится неточным из-за больших погрешностей в графических построениях на морских навигационных картах мелкого масштаба.
Чаще всего аналитическое счисление применяется:

→ при непрерывной выработке текущих счислимых координат места судна, вводимых в системы судовой автоматики. Задача решается с помощью автоматических счетно-решающих устройств (или ЭВМ);
→ при периодическом вычислении счислимых координат места судна в тех случаях, когда необходимо исключить погрешности счисления за счет неточности графических построений, связанных с прокладкой пути судна на мелкомасштабной карте. Задача решается вручную или с помощью счетно-решающих устройств (для контроля точности графических построений на карте; определения места судна по разновременным наблюдениям светил).

Аналитическое счисление с помощью автоматических счетно-решающих устройств производится по формулам с учетом сжатия Земли. В простейших системах решаются формулы без учета сжатия Земли.

следуя постоянным курсом (К) по локсодромии, пришло в точку В

Значение разности широт (РШ) и разности долгот (РД) можно рассчитать по известным элементам движения: К → курсу судна и S → плаванию судна по этому курсу.
Считая Землю за сферу (шар) из элементарно малого треугольника Аа′в′:
Aa′ = dφ → приращение широты; b′a′ = dω → приращение отшествия; Ab′ = dS → приращение расстояния,

результате интегрирования значений dφ и dω при K = const,

то есть

то есть

Для вычисления значения разности долгот – РД, воспользуемся соотношением между длиной дуги экватора и параллели:

Умножим числитель (dω) и знаменатель (cos φ)
на dφ, тогда

так как из Δ Аа′в′

то

Решение этого уравнения
приводит к
известному интегралу:

а

тогда

Для вывода прямой связи между отшествием (ОТШ) и разностью долгот (РД),
используем
теорему о среднем значении интеграла, которая дает:

и φ2.
Тогда для разности долгот – РД можно написать:
Приравняв оба

откуда

Подставив значение соs φn (формула 17.8) в формулу (17.6)
для разности долгот (РД) и учтя, что

окончательно получим:

где отшествие (ОТШ) и разность широт (РШ) в милях.
Таким образом отшествие (ОТШ) представляет собой длину параллели (в милях)
между меридианами точек А и В, широта которой (параллели) определяется соотношением

допустить, что в интервале от φ1 до φ2 значение cos

и приближенная формула для расчета
разности долгот – РД примет вид:

то есть разность долгот (РД) равна отшествию (ОТШ), деленному на косинус средней широты (φm).
По формулам (17.3) и (17.4) составлены таблица 24 «МТ-75» (с. 260÷272) и таблица 2.19а «МТ-2000» (с. 282÷294) «Разность широт и отшествие». В этих таблицах по плаванию S (от 0 до 100 миль) и курсу (через 1°) можно получить готовые значения разности широт (РШ) и отшествия (ОТШ), величины которых даны в таблице до сотых долей мили и поэтому могут быть использованы для плаваний (S) в 10 и 100 раз больших (или меньших) → переносом запятой → см. табл. 17.8.

(с. 273÷278)
составленная по формуле (17.13).
Аналогичная таблица 2.20 – см.

Получение значений разности долгот (РД) для десятков или сотен миль значений отшествия (ОТШ) делается простым переносом запятой, отделяющей целую часть от дробной в найденных табличных значениях.

+ 6.
По значениям 100, 100, 40 и 6 для φCP

Таблица 17.2.

Ответ: РД = 321,0′ к W.

Решение:
1. → Находим значение φn (см. ф. 17.8).

φ1 = 60°N …. МЧ1 = 4507,4′
φ2 = 20°N…. МЧ2 = 1217,3′

Значения меридиональных частей (МЧ1 и МЧ2) выбираем из табл. 26 «МТ-75» (с. 280÷287) или табл. 2.28а «МТ-2000» (с. 314÷321) → табл. 24.5.

«МТ-2000» (с. 322) «Поправки для получения меридиональных частей шара» выбираем

В результате:

и φn = 43°23′ ≈ 43,4° (см. табл. 6а «МТ-75» (с. 156÷199)
или табл. 5.42а «МТ-2000» (с. 460)
«Натуральные значения тригонометрических функций» → табл. 24.6.
2) → Разбиваем значение отшествия – ОТШ = 246′ = 100 + 100 + 40 + 6 и
выбираем соответствующие им (100, 100, 40, 6)
значения разности долгот – РД из табл. 25а «МТ-75» или 2.20 «МТ-2000»,
интерполированием между φn = 43° и φn = 43,5°
(см. табл. 17.3).

Сравнивая значение разности долгот из табл. 17.2 (РД1 = 321,0′ к W) и значение разности долгот из табл. 17.3 (РД2 = 338,6′ к W) видно (Δ = 17,6′), что при больших значениях разности широт (РШ), нужно пользоваться не средним значением широты (φСР), а значением промежуточной широты (φПР).