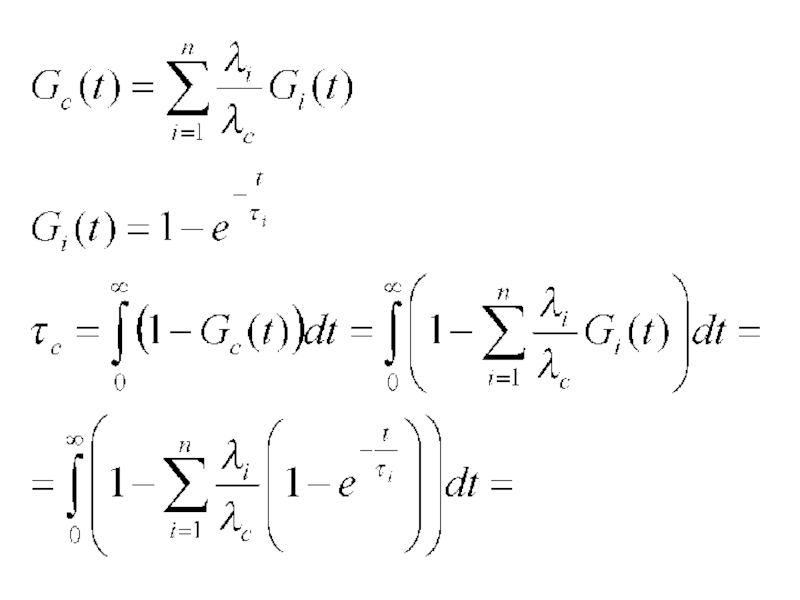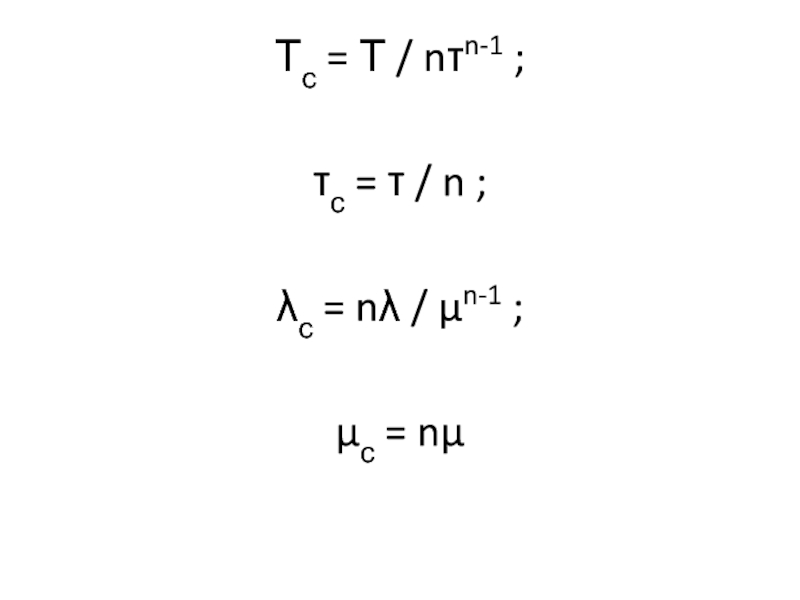Слайд 1Глава 3. Показатели надежности
3.1. Невосстанавливаемые объекты
Пусть при t = 0
объект начинает работу;
при t = Т происходит отказ объекта.
Т –
НСВ, которая называется наработка до отказа.
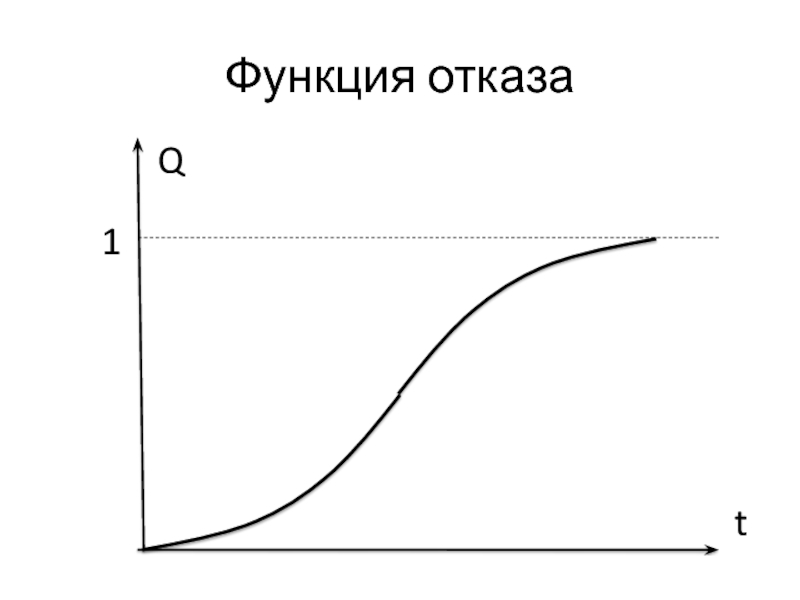
Обозначим функцию распределения этой НСВ Q(t).
Назовём Q(t) функцией отказа.
По определению:
Q(t) = P(T < t) – вероятность отказа объекта до момента t.
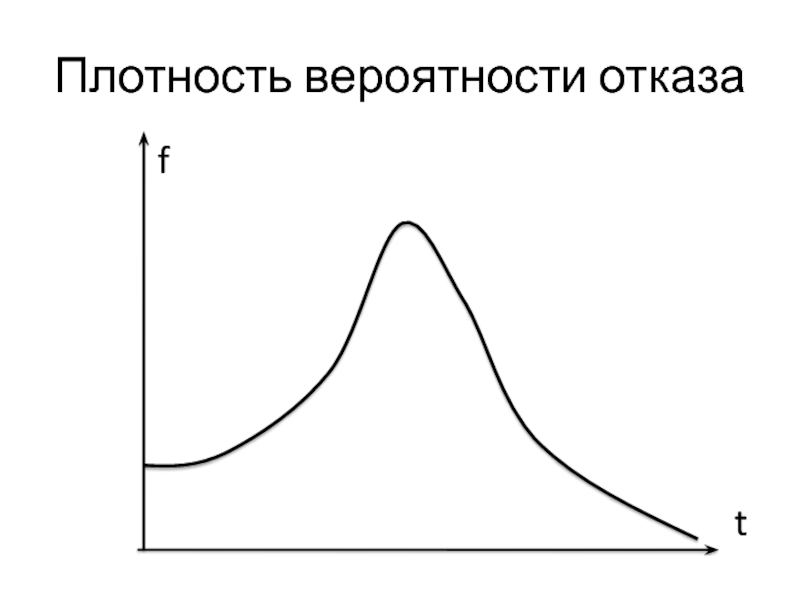
Слайд 3Введем понятие плотности вероятности отказа объекта f(t).
Аналитически:
f(t) = Q’(t).
Статистически:
где
m(t) – количество объектов, отказавших к моменту времени t;
N(t) –
количество объектов, исправных к моменту времени t;
N0 – количество объектов, исправных при t = 0.
Слайд 4Плотность вероятности отказа
f
t
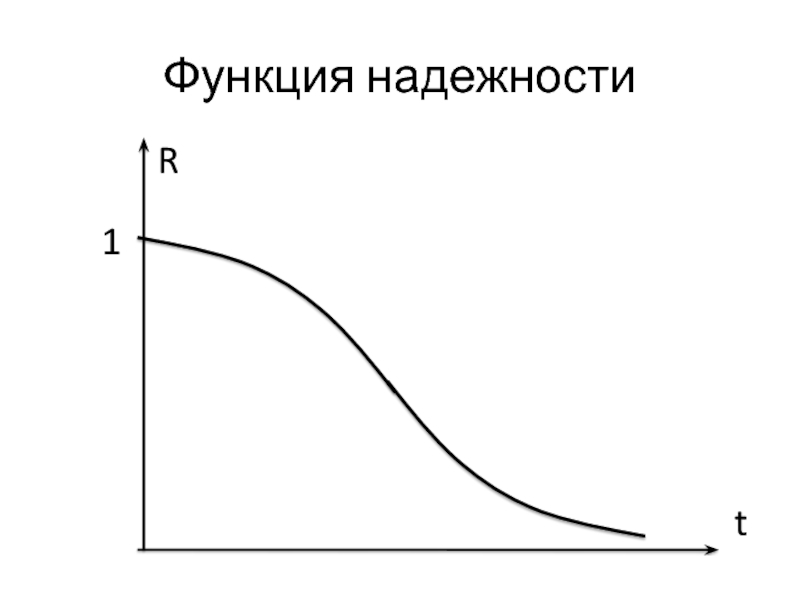
Слайд 5Обозначим вероятность безотказной работы в течение времени t:
R(t) = P(T
> t)
Назовём R(t) функцией надежности.
Аналитически:
R(t) = 1 – Q(t).
Статистически:
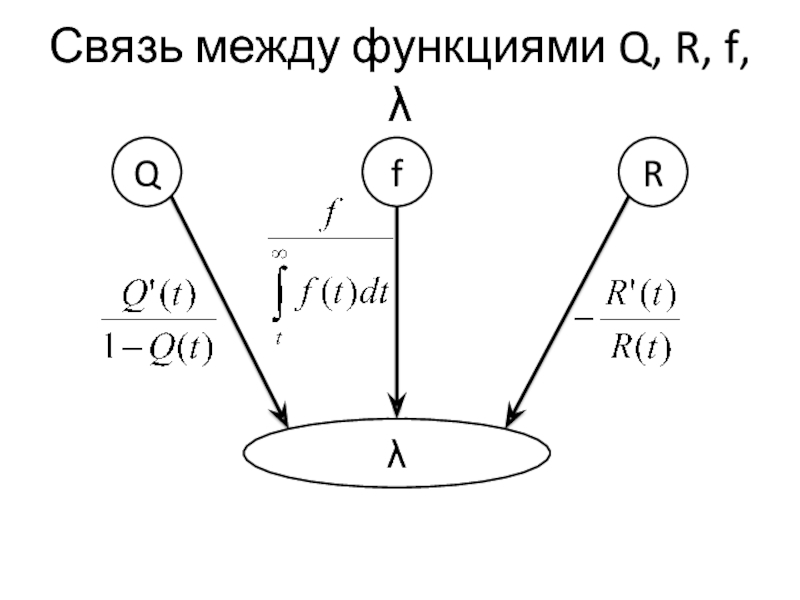
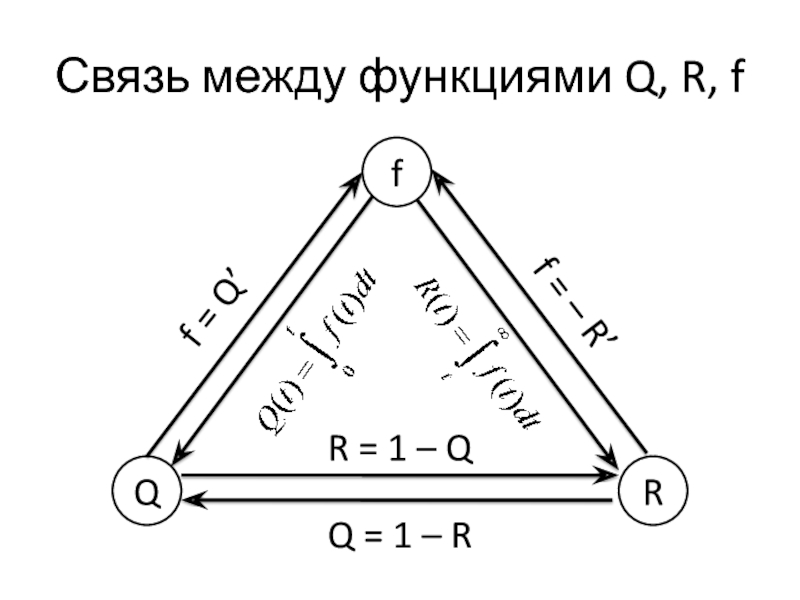
Слайд 7Связь между функциями Q, R, f
Q
R
f
Q = 1 – R
R
= 1 – Q
f = Q’
f = – R’
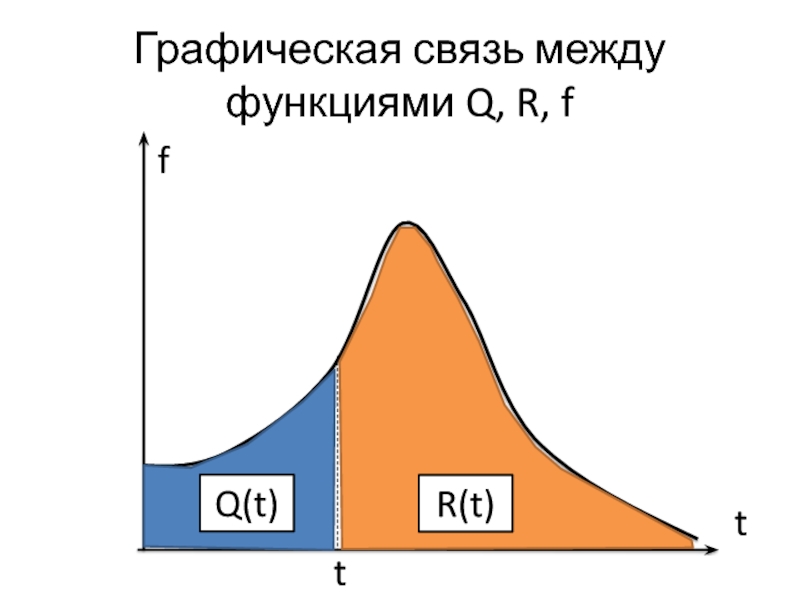
Слайд 8Графическая связь между функциями Q, R, f
f
t
t
Q(t)
R(t)
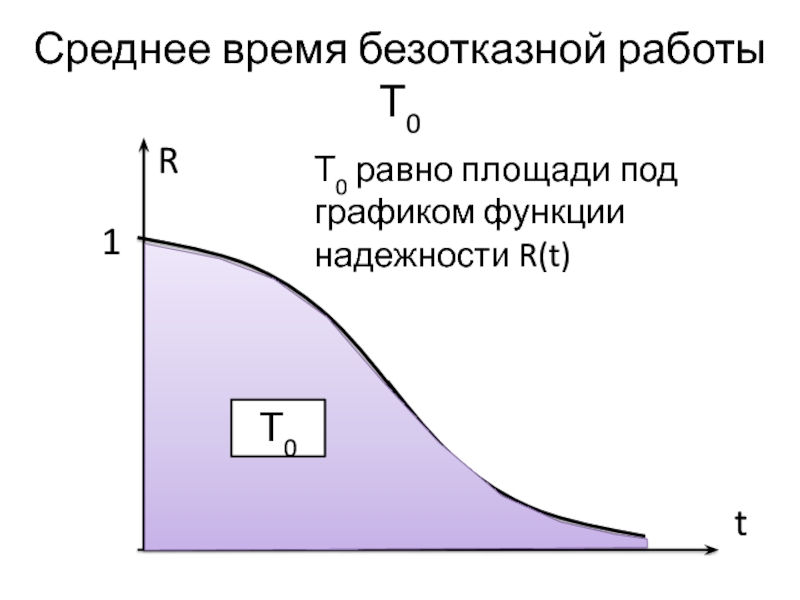
Слайд 9Среднее время безотказной работы Т0
R
t
1
Т0
Т0 равно площади под графиком функции
надежности R(t)
Слайд 10Среднее время безотказной работы Т0
Статистически:
где
ti – наработка до отказа
i-го объекта;
N0 – первоначальное количество исправных объектов.
Причём испытания проводят, пока
все N0 объектов не откажут.
Слайд 11Среднее время безотказной работы Т0
Если нет возможности дожидаться отказа всех
объектов (из-за недостатка времени), то Т0 можно оценить так:
где
t
– время испытания;
m – число отказавших объектов за время t
Слайд 12Интенсивность отказов λ(t)
[λ] = с-1, ч-1, год-1 и т. д.
Статистически:
λ(t)
– число отказов в единицу времени, отнесённое к числу безотказно
проработавших до этого времени объектов.
С позиций теории вероятности:
λ(t) – условная плотность вероятности отказа объекта при условии, что до рассматриваемого момента отказа не было.
Таким образом λ(t) является локальной характеристикой надёжности, т.е. определяет надёжность объекта в каждый данный момент времени.
Слайд 13Интенсивность отказов λ(t)
Аналитически:
Статистически:
где m(Δt) – количество отказов за время Δt.
Слайд 14Связь между функциями Q, R, f, λ
Q
R
f
λ
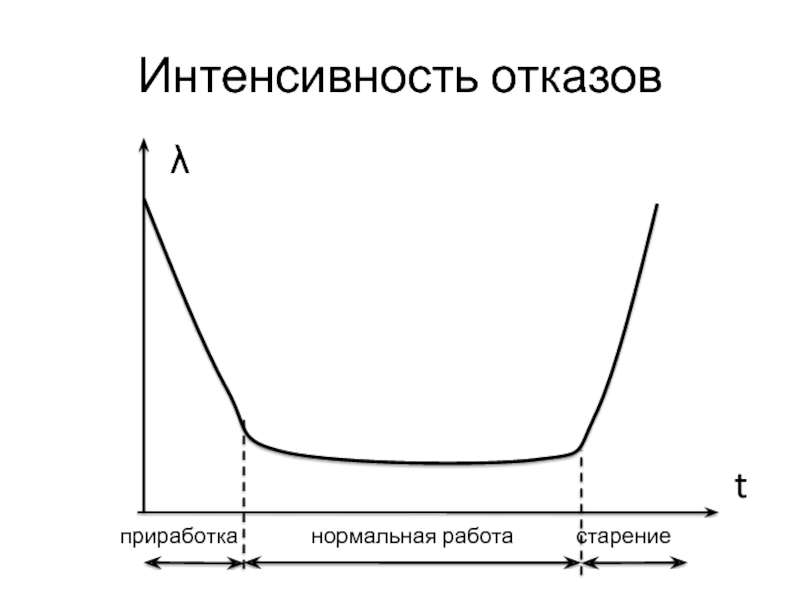
Слайд 15Интенсивность отказов
λ
t
приработка
нормальная работа
старение
Слайд 16Для нормальной работы можно считать:
λ(t) = const = λ
Тогда
R(t) =
exp(– λt)
Q(t) = 1 – exp(– λt)
f(t) = λexp(– λt)
T0
= 1/λ
Получили экспоненциальный закон распределения с параметром λ.
Слайд 17При экспоненциальном законе вероятность безотказной работы на интервале (t; t
+ Δt) не зависит от времени предшествующей работы t, а
зависит только от продолжительности интервала Δt.
Доказательство:
R(t; t + Δt) = exp(– λΔt)
По формуле условной вероятности
R(t; t + Δt) = R(t + Δt) / R(t) =
= exp(– λ(t + Δt)) / exp(– λt) =
= exp(– λ(t + Δt) + λt)
Слайд 18Упрощение формул для малых времён t
В практических расчетах при малых
временах рассмотренные выше формулы упрощают, используя соотношение из теории эквивалентов:
exp(x)
~ 1 + x при х → 0
Тогда
R(t) = 1 – λt
R(t; t + Δt) = 1 – λΔt
Q(t) = λt
Эти зависимости верны для малых λt (т.е. t << T0).
Слайд 193.2. Объекты с мгновенным восстановлением
Эксплуатация восстанавливаемого объекта не прекращается при
его отказе.
Объект ремонтируется или заменяется новым.
Наработка между отказами и продолжительность
восстановления являются НСВ.
Рассмотрим ситуацию, когда время восстановления << наработки между отказами.
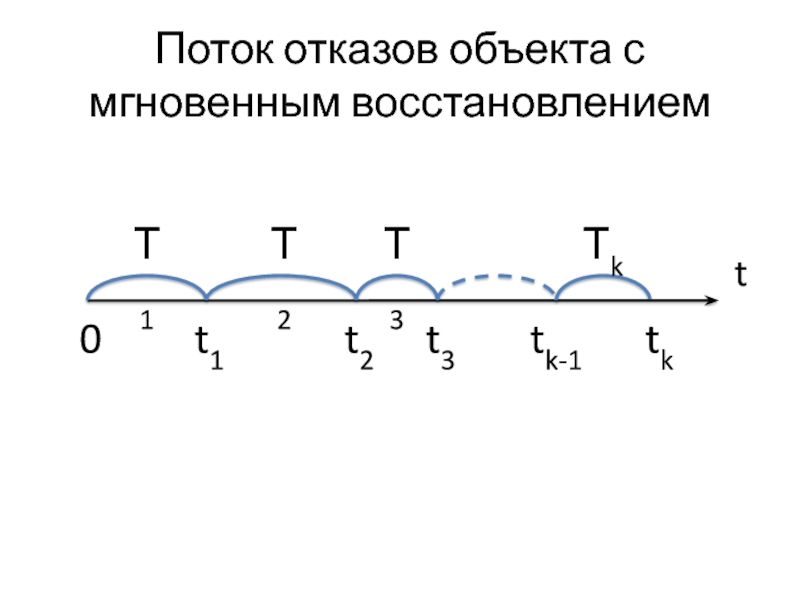
Слайд 20Поток отказов объекта с мгновенным восстановлением
t
Т1
Т2
Т3
Тk
t1
t2
t3
tk
tk-1
0
Слайд 21Рассмотрим плотности вероятностей времени:
до первого отказа f1(t);
до второго отказа f2(t);
…
до
k-го отказа fk(t).
Пусть первый отказ произошёл в момент τ;
пусть второй
отказ произошёл в момент t.
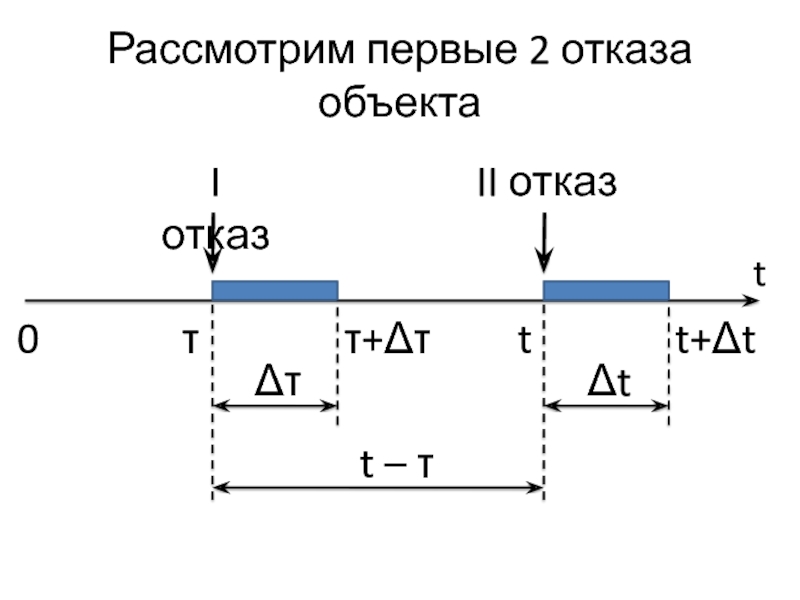
Слайд 22Рассмотрим первые 2 отказа объекта
t
I отказ
τ
τ+Δτ
Δτ
t+Δt
t
0
II отказ
Δt
t – τ
Слайд 23Выведем формулу для f2(t)
Наработка на второй отказ равна t –
τ.
Рассмотрим вероятность того, что второй отказ произойдёт на интервале (t;
t + Δt):
Δf2(t) Δt = f1(τ) Δτ ∙ f1(t – τ) Δt
Разделим на Δt и проинтегрируем по τ от 0 до t:
Слайд 24Обобщим этот результат на k отказов.
Выведем формулу для fk(t).
Пояснение:
Дошли до
(k – 1)-го отказа,
зафиксировали накопившуюся вероятность
и начали отсчёт
времени с нуля.
Значит, следующий отказ будет первым =>
=> в интеграле имеется f1(t).
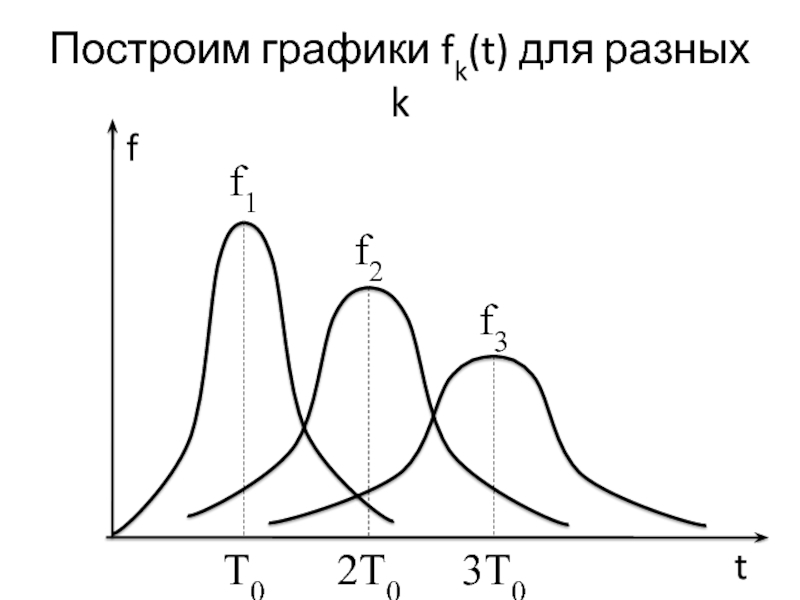
Слайд 25Построим графики fk(t) для разных k
f
t
2T0
T0
3T0
f1
f2
f3
Слайд 26Свойства графиков fk(t)
Каждый график fk(t) имеет максимум в точке
t
= kТ0.
Каждый график fk(t) приблизительно симметричен относительно оси t =
kТ0.
Максимальное значение функции fk(t) уменьшается с ростом k, т.к. накапливаются неопределённости по предыдущим наработкам.
Кривая fk(t) становится более пологой (широкой) с ростом k.
Слайд 27Параметр потока отказов ω(t)
Назовём сумму
f1(t) + f2(t) + … +
fk(t) = ω(t)
параметром потока отказов.
По сути ω(t) – это
плотность вероятности отказа.
С одной стороны функция ω(t) является локальной по времени, с другой стороны она охватывает одновременно все отказы, т.е. является глобальной по отказам.
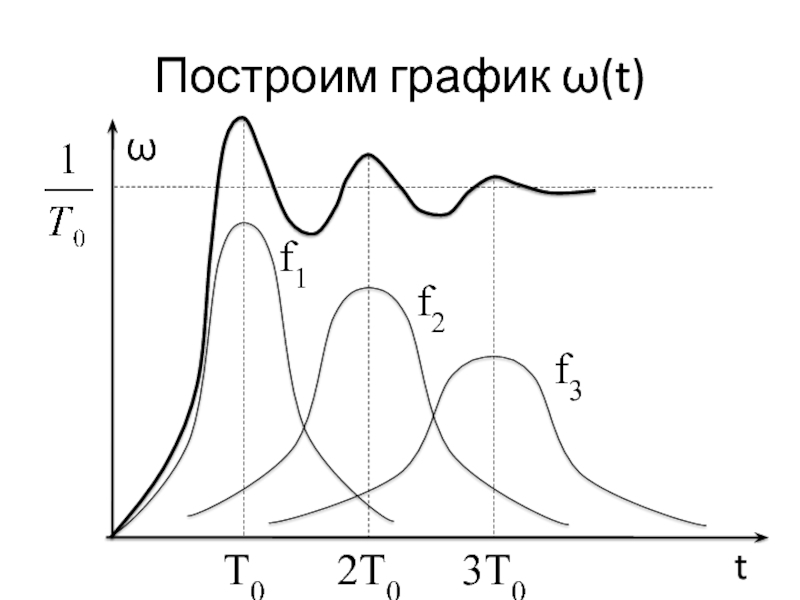
Слайд 28Построим график ω(t)
ω
t
2T0
T0
3T0
f1
f2
f3
Слайд 29Свойство графика ω(t)
График ω(t) имеет максимумы в точках
t =
kТ0.
Кривая ω(t) стабилизируется с течением времени и с ростом k
на уровне 1/Т0, т.е. процесс возникновения отказов становится стационарным, его локальные характеристики перестают зависеть от времени.
Слайд 30Свойства потоков отказов
Потоки отказов могут обладать свойствами:
Свойство ординарности. Вероятность совмещение
2-х и более отказов в один момент времени равна нулю.
Свойство
отсутствия последействия. Числа отказов для любых неперекрывающихся интервалов времени независимы.
Свойство стационарности. Вероятность появления k отказов на любом промежутке времени зависит только от числа k и от длительности Δt и не зависит от начала отсчёта времени.
Слайд 31Виды потоков отказов
Если выполняется (1),
то поток ординарный.
Если выполняются (1)
и (2),
то поток пуассоновский.
Если выполняются (1), (2), (3),
то
поток простейший.
Слайд 32Для простейшего потока:
f1(t) = λ exp(–λt)
f2(t) = λ2 exp(–λt)
…
ω(t) =
λ
T0 = 1/λ
Слайд 33Для простейшего потока:
Вероятность k отказов за время t:
Вероятность безотказной работы
за время t:
P0(t) = exp(–λt)
Слайд 343.3. Объекты с конечным временем восстановления
Время восстановления τ = tп
+ tр
tп – поиск неисправности;
tр – ремонт или замена.
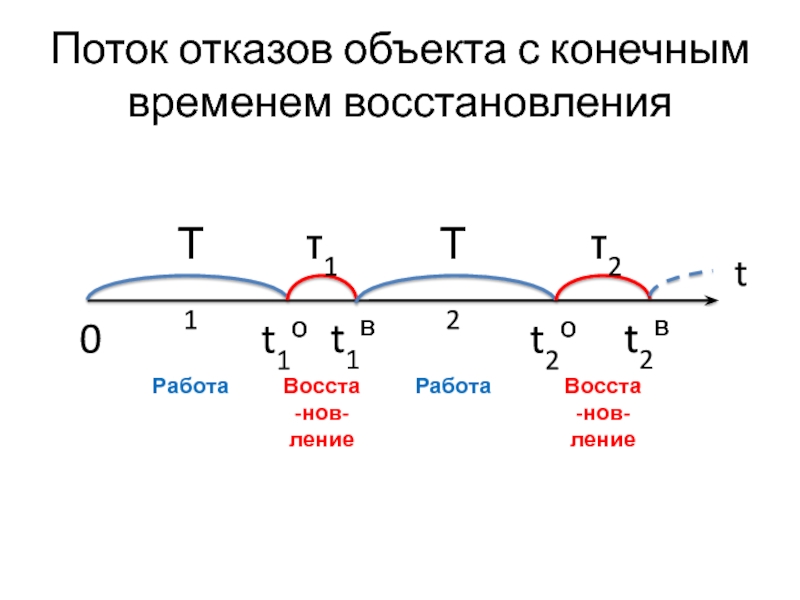
Пусть объект,
проработав время T1, выходит из строя и восстанавливается в течение τ1.
Восстановленный объект через T2 вновь отказывает, за τ2 снова восстанавливается и т.д.
Слайд 35Поток отказов объекта с конечным временем восстановления
t
Т1
τ1
Т2
τ2
t1о
0
t1в
t2о
t2в
Работа
Восста-нов-ление
Работа
Восста-нов-ление
Слайд 36Сделаем допущения:
1) Тk, τk – независимые НСВ.
2) Все периоды работы
Тk имеют:
- законы F(t), f(t);
- среднюю наработку на отказ Т
= М(Тk);
- интенсивность отказов λ = 1/Т.
3) Все периоды восстановления τk имеют:
- законы G(t), g(t);
- среднее время восстановления τ = М(τk) ;
- интенсивность восстановлений μ = 1/τ.
4) Поток отказов и восстановлений – простейший.
Слайд 37Введём понятие коэффициента готовности Кг(t)
Кг(t) – это вероятность того, что
в момент времени t объект находится в работоспособном состоянии (РСС).
Найдём
зависимость Кг(t).
Вероятность застать объект в РСС в момент (t + Δt) зависит от его состояния в момент t и его поведения на интервале Δt.
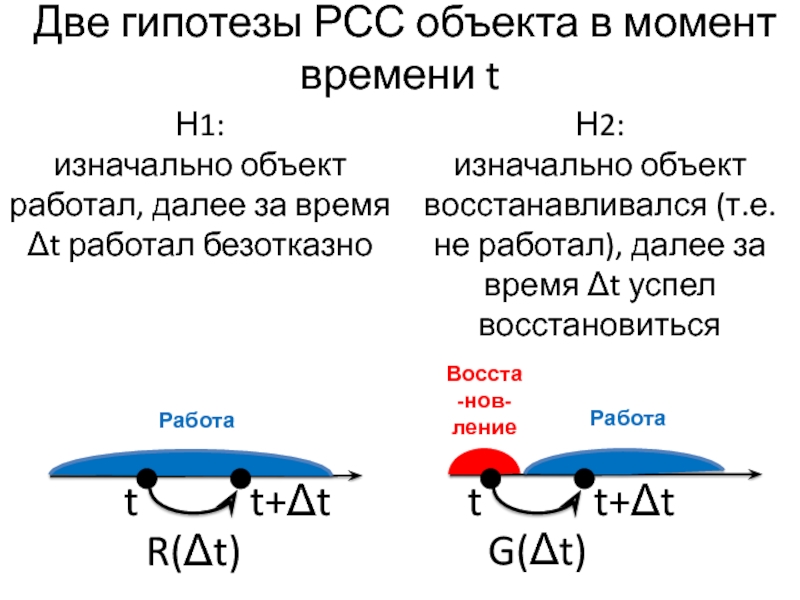
Слайд 38Две гипотезы РСС объекта в момент времени t
t
Работа
Работа
Восста-нов-ление
t+Δt
t
t+Δt
Н1:
изначально объект работал,
далее за время Δt работал безотказно
Н2:
изначально объект восстанавливался (т.е. не
работал), далее за время Δt успел восстановиться
R(Δt)
G(Δt)
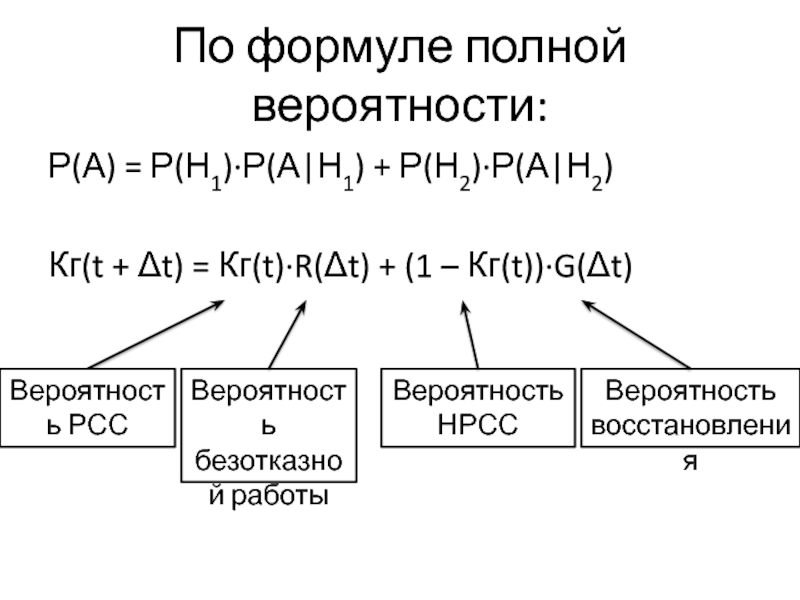
Слайд 39По формуле полной вероятности:
Р(А) = Р(Н1)∙Р(А|Н1) + Р(Н2)∙Р(А|Н2)
Кг(t +
Δt) = Кг(t)∙R(Δt) + (1 – Кг(t))∙G(Δt)
Вероятность РСС
Вероятность безотказной
работы
Вероятность НРСС
Вероятность восстановления
Слайд 40В разделе 3.1 доказано, что:
R(Δt) = 1 – λΔt;
G(Δt)
= μΔt.
Подставим:
Слайд 42Коэффициент неготовности – вероятность нахождения объекта в НРСС.
Кнг = 1
– Кг
Кнг(0) = 0
Кнг(∞) = λ/(λ+μ) = τ/(Т+τ)
график Кнг(t)
Коэффициент
аварийного простоя – относительная длительность восстановления.
qав = λ/μ = τ/Т
Слайд 43Глава 4. Вероятностные модели для расчёта надёжности
4.1. Общие положения
Система состоит
из множества элементов.
Надёжность системы зависит от надёжности её элементов и
от её конфигурации.
Каждый элемент системы и сама система могут находиться только в двух состояниях – работы или отказа.
Если все элементы системы работают, то и сама система тоже работает.
Если все элементы отказали, то и система отказала.
Слайд 44Введем обозначения
Аi – событие безотказной работы i-го элемента;
Аi – событие
отказа i-го элемента;
Ас – событие безотказной работы системы;
Ас – событие
отказа системы;
Слайд 45Системы отображаются в виде:
физических схем:
они имеют действительные, электрические связи;
логических (расчётных)
схем:
они отражают логические связи, в смысле надёжности.
Отказом системы считают отсутствие
связи между началом и концом логической схемы.
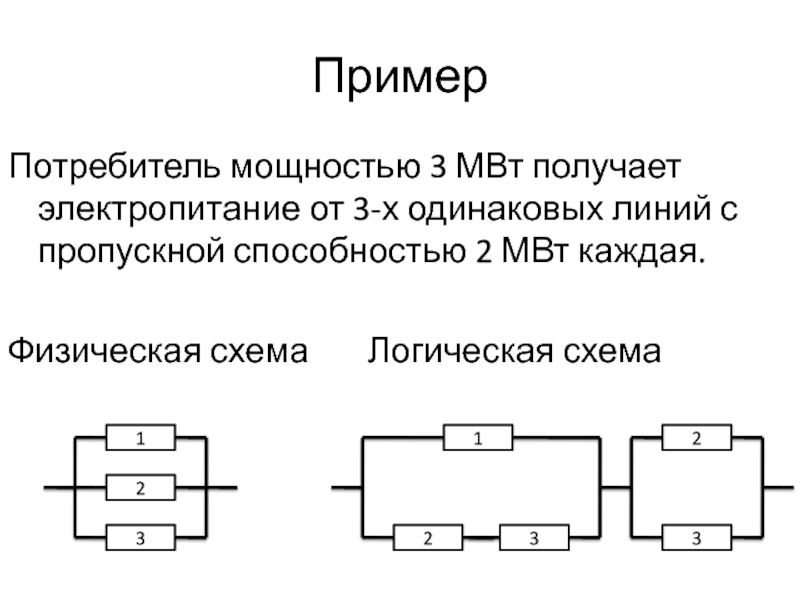
Слайд 46Пример
Потребитель мощностью 3 МВт получает электропитание от 3-х одинаковых линий
с пропускной способностью 2 МВт каждая.
Физическая схема Логическая схема
1
2
3
1
2
3
2
3
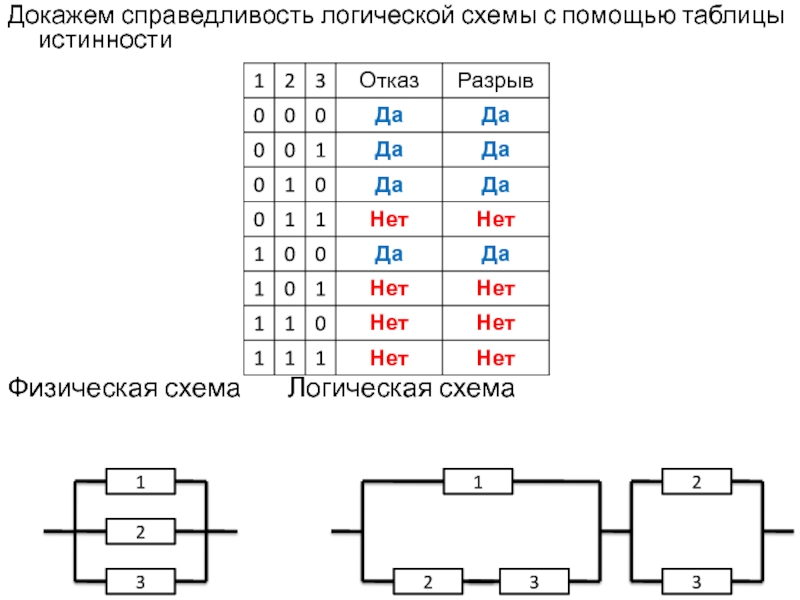
Слайд 47Докажем справедливость логической схемы с помощью таблицы истинности
Физическая схема Логическая схема
1
2
3
1
2
3
2
3
Слайд 484.2. Последовательное соединение элементов
Последовательным (в смысле надёжности) называют такое соединение,
при котором отказ одного элемента приводит к отказу всей системы,
но не изменяет надёжности других элементов.
Тогда вероятность безотказной работы системы равна системы равна произведению б.о.р. всех элементов:
Р(Ас) = Р(А1) ∙ Р(А2) ∙ … ∙ Р(Аn)
Слайд 494.2.1. При отсутствии восстановления элементов
Вероятность б.о.р. системы, состоящей из независимых
и невосстанавливаемых элементов в течение времени t:
Rс(t) = R1(t) ∙
R2(t) ∙ … ∙ Rn(t)
Т.к. Ri(t) = exp(– λit), то
Rс(t) = exp(– λ1t) ∙ exp(– λ2t) ∙ … ∙ exp(– λnt) =
= exp(– (λ1 + λ2 + … + λn)t)
Слайд 50С другой стороны
Rс(t) = exp(– λсt)
Значит
λс = λ1 +
λ2 + … + λn
1/Тс = 1/Т1 + 1/Т2
+ … + 1/Тn ;
Тс = 1/(1/Т1 + 1/Т2 + … + 1/Тn)
Слайд 514.2.2. При мгновенном восстановлении элементов
Число отказов системы равно сумме чисел
отказов элементов.
Допустим, за время t:
элемент 1 претерпевает h1 отказов;
элемент 2
претерпевает h2 отказов;
…
элемент n претерпевает hn отказов.
Рассмотрим поток отказов системы:
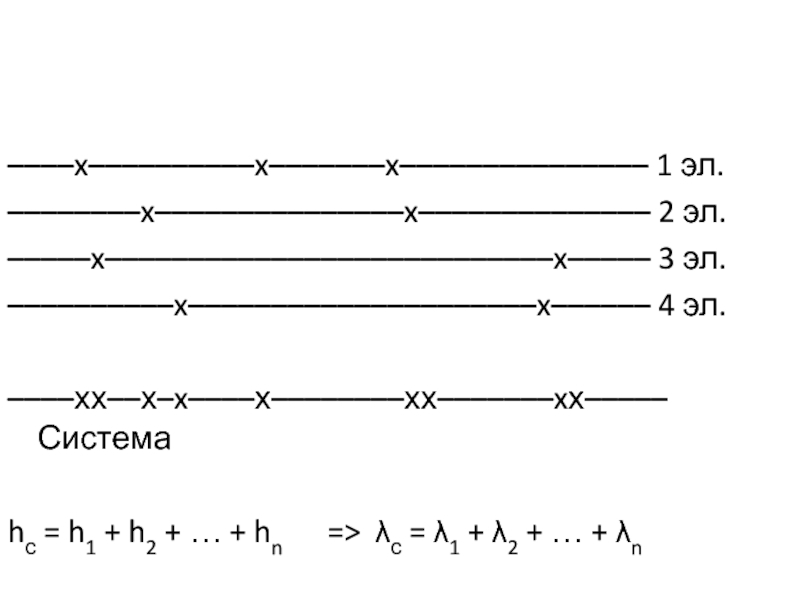
Слайд 52––––x––––––––––x–––––––x––––––––––––––– 1 эл.
––––––––x–––––––––––––––x–––––––––––––– 2 эл.
–––––x–––––––––––––––––––––––––––x––––– 3 эл.
––––––––––x–––––––––––––––––––––x–––––– 4 эл.
––––хх––х–x––––х––––––––хх–––––––xх––––– Система
hс
= h1 + h2 + … + hn => λс
= λ1 + λ2 + … + λn
Слайд 53Вероятность появления k отказов на интервале Δt:
Вероятность б.о.р. системы:
R(t) =
exp(– λсt) = exp(– t/Тс)
Слайд 544.2.3. При конечном времени восстановления
В этом случае при отказе элемента,
на время его восстановления отключается вся система.
После окончания восстановления
элемента все элементы начинают работать так, как если бы восстановление происходило мгновенно.
Слайд 55Дано:
последовательность средних периодов б.о.р. элементов:
Т1, Т2, …;
со средним временем б.о.р.
системы:
Тс = 1/(1/Т1 + 1/Т2 + …)
и последовательность средних
периодов восстановления элементов:
τ1, τ2, …
Найти среднюю длительность восстановления системы τс
Слайд 56Решение
Вероятность отказа i-го элемента на отрезке Δt:
λi Δt
Вероятность отказа системы
на отрезке Δt:
λс Δt
Тогда условная вероятность отказа i-го элемента при
условии, что на этом же интервале отказала система, равна:
λi Δt / λс Δt = λi / λс
По формуле полной вероятности найдём распределение длительности восстановления для системы, начавшегося в момент t:
Gc(t) =
Слайд 58Формулы для средней длительности восстановления системы
Слайд 59Выведем коэффициент готовности системы через Тi, τi
Слайд 614.3. Параллельное соединение элементов
4.3.1. Резервирование одного элемента (n-1) резервным
Система с
параллельным ( в смысле надёжности) соединением элементов выходит из строя
только в случае отказа всех её элементов.
Слайд 62Вероятность отказа такой системы равна:
Р(Ас) = Р(А1) ∙ Р(А2) ∙
… ∙ Р(Аn)
(при этом считаем, что отказы всех элементов независимы).
Вероятность
б.о.р. системы равна:
Р(Ас) = 1 – (1 – Р(А1)) ∙ (1 – Р(А2)) ∙ … ∙ (1 – Р(Аn))
Вероятность отказа системы:
Qс(t) = Q1(t) ∙ Q2(t) ∙ … ∙ Qn(t)
Вероятность б.о.р. системы равна:
Rc(t) = 1 – (1 – R1(t)) ∙ (1 – R2(t)) ∙ … ∙ (1 – Rn(t))
Слайд 63При равнонадежных элементах и экспоненциаль-ном законе:
Qс(t) = (1 – exp(–
λt))n,
где λ – частота отказа элемента схемы.
Вычислим среднее время б.о.р.
системы:
Тс =
Слайд 64При n → ∞
Тс = ln(n)/λ
Например:
n = 100: Тс =
4,6/λ
n = 1 000: Тс = 6,9/λ
n = 10 000:
Тс = 9,2/λ
Вычислим параметры системы Тс , τс , λс , μс через параметры равнонадёжных элементов Т, τ, λ, μ:
Вывод формул выполним через величины:
qс , q – вероятности застать систему и элемент в состоянии простоя.
Слайд 65Тс = Т / nτn-1 ;
τс = τ /
n ;
λс = nλ / μn-1 ;
μс = nμ
Слайд 664.3.2. Резервирование r рабочих элементов (n – r) резервными
Пусть система
состоит из n элементов.
Пусть для нормального функционирования системы необходимо r
элементов.
Тогда остальные (n – r) элементов являются резервными.
Отказ системы наступает при выходе из строя
(n – r + 1) элементов.
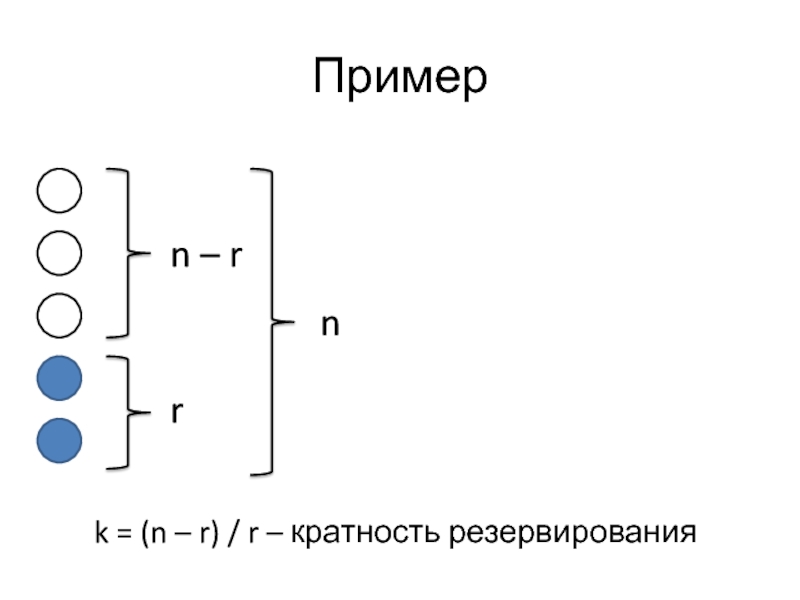
Слайд 67Пример
k = (n – r) / r – кратность резервирования
n
– r
r
n
Слайд 68Как рассчитать функции надежности Rc и отказа Qс всей системы,
зная Ri и Qi каждого элемента?
В общем виде – громоздкое
выражение, поэтому примем допущение, что все элементы равнонадёжны и имеют функции
R1 = R2 = … = R,
Q1 = Q2 = … = Q.
Сначала выведем формулы для частного случая.
Слайд 69Пример
Дано: Найти:
n = 5 Rc
r = 2 Qc
n – r + 1 =
4
k = 1,5
R
Q
Слайд 70Решение
Очевидно, что для системы:
Rc + Qc = 1
и для каждого
элемента:
R + Q = 1
Отсюда следует, что:
Rc + Qc =
(R + Q)5 =
= R5 + 5R4Q + 10R3Q2 + 10R2Q3 + 5RQ4 + Q5
Слайд 71Обобщим результаты этого примера
Слайд 72Виды резервирования
По способу включения резервных элементов резервирование бывает:
постоянное (резервные объекты
включены в систему в течение всего времени работы и находятся
в одинаковых с другими объектами условиях)
замещением (резервные объекты включают в систему вместо основных после отказа последних)
Слайд 73Постоянное резервирование (неявное)
Отказавший элемент должен отключаться защитной аппаратурой, надёжность которой
будет определять надёжность всей схемы.
Слайд 74Резервирование замещением (явное)
Отказавший элемент должен отключаться защитной аппаратурой, а резервный
элемент должен включаться аппаратурой автоматики.
Надёжность этих видов аппаратуры будет определять
надёжность всей схемы.
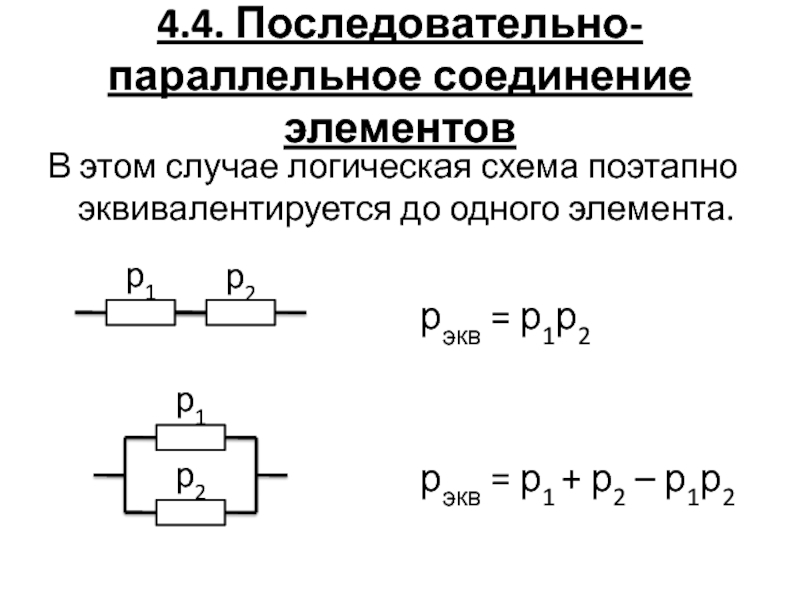
Слайд 754.4. Последовательно-параллельное соединение элементов
В этом случае логическая схема поэтапно эквивалентируется
до одного элемента.
р1
р2
р1
р2
рэкв = р1р2
рэкв = р1 + р2 –
р1р2
Слайд 76Полезно помнить, что:
при последовательном соединении робщ меньше меньшего;
при параллельном соединении
робщ больше большего, но меньше 1.
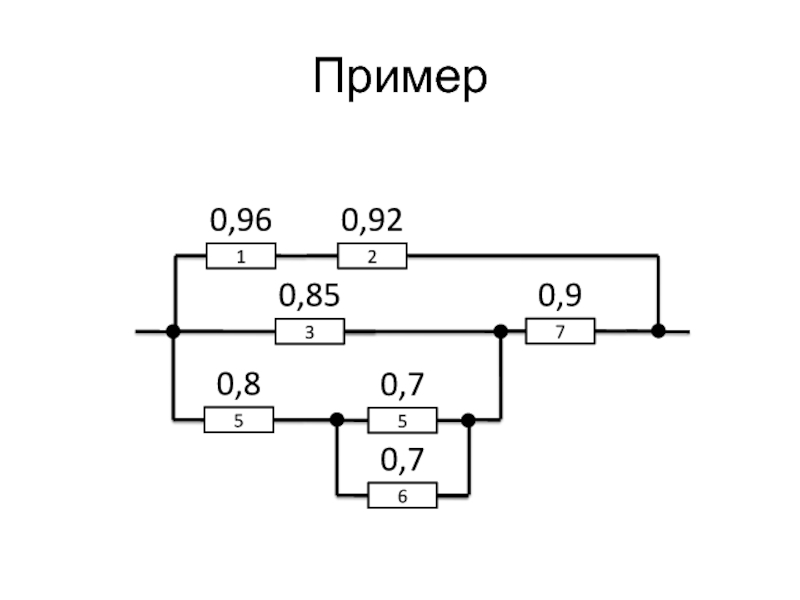
Слайд 77Пример
1
2
0,96
0,92
3
0,85
5
0,8
5
0,7
6
0,7
7
0,9
Слайд 79Вывод
За счёт параллельных связей надёжность системы выше надёжности каждого элемента.
Слайд 804.5. Метод минимальных путей и сечений
Этот метод применяют, когда структуру
системы нельзя свести к последовательно-параллельным цепочкам.
Введем следующие понятия:
Путь – последовательность
смежных элементов, соединяющая вход и выход схемы.
Сечение – совокупность элементов, удаление которых приводит к нарушению связи между входом выходом.
Слайд 81Минимальный путь – путь, удаление из которого хотя бы одного
элемента приводит к тому, что оставшееся множество элементов не будет
путём.
Минимальное сечение – сечение, удаление из которого хотя бы одного элемента приводит к тому, что оставшееся множество элементов перестаёт быть сечением.
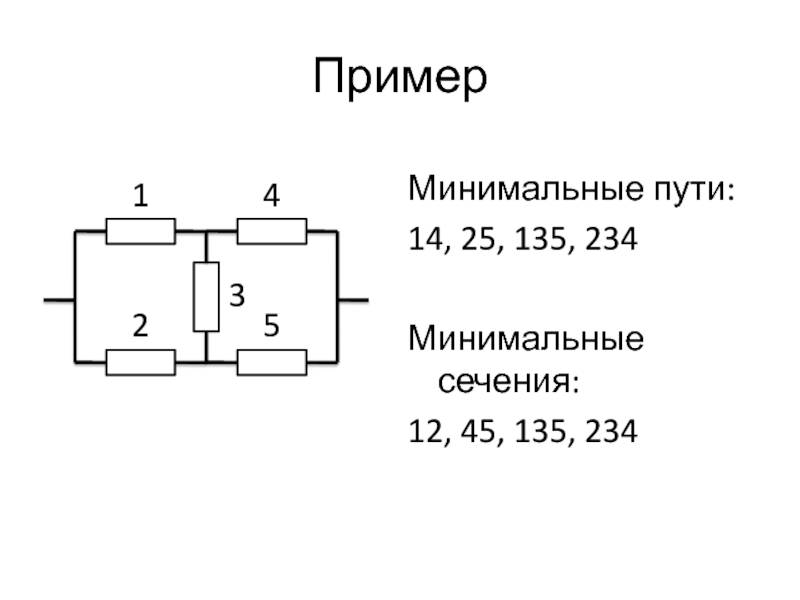
Слайд 82Пример
Минимальные пути:
14, 25, 135, 234
Минимальные сечения:
12, 45, 135, 234
1
2
4
5
3
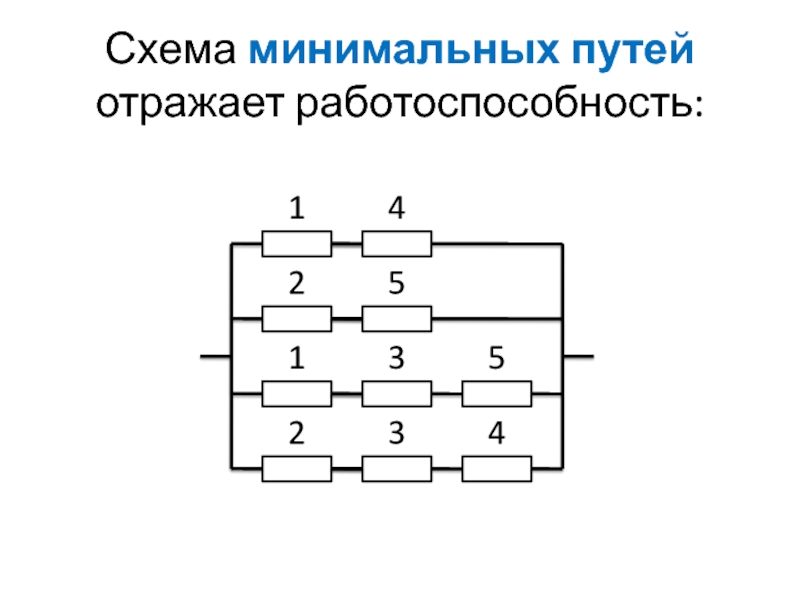
Слайд 83Схема минимальных путей отражает работоспособность:
1
4
2
5
1
3
2
3
5
4
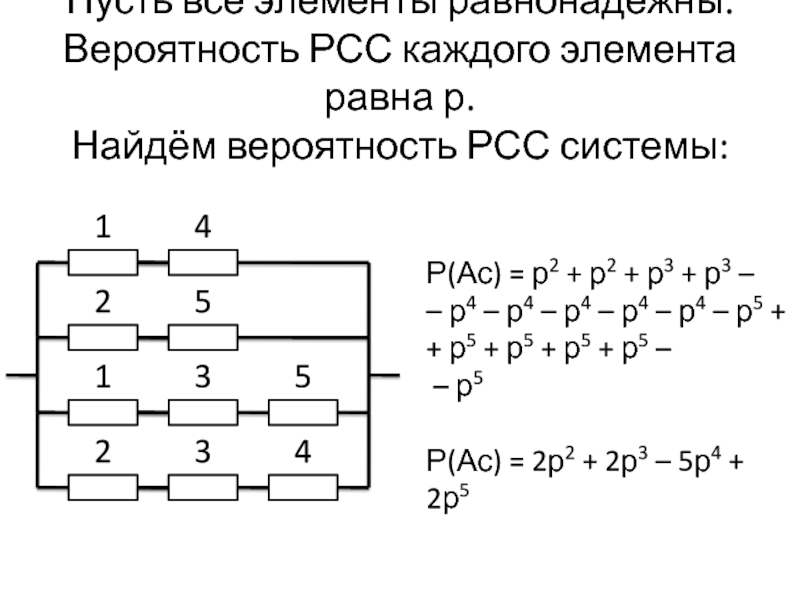
Слайд 84Пусть все элементы равнонадежны. Вероятность РСС каждого элемента равна р.
Найдём
вероятность РСС системы:
1
4
2
5
1
3
2
3
5
4
Р(Ас) = р2 + р2 + р3 +
р3 –
– р4 – р4 – р4 – р4 – р4 – р5 +
+ р5 + р5 + р5 + р5 –
– р5
Р(Ас) = 2р2 + 2р3 – 5р4 + 2р5





![Глава 3. Показатели надежности Интенсивность отказов λ(t)[λ] = с-1, ч-1, год-1 и т. д.Статистически:λ(t) – Интенсивность отказов λ(t)[λ] = с-1, ч-1, год-1 и т. д.Статистически:λ(t) – число отказов в единицу времени, отнесённое](/img/thumbs/e13689ebcad3dd68d8691e45d82ae944-800x.jpg)